浅部频率域电磁勘探方法综述

汤井田， 任政勇， 周聪， 张林成， 原源， 肖晓

1 中南大学有色金属成矿预测与地质环境监测教育部重点实验室， 长沙 410083 2 中南大学地球科学与信息物理学院, 长沙 410083



浅部频率域电磁勘探方法综述

汤井田1,2， 任政勇1,2， 周聪1,2， 张林成1,2， 原源1,2， 肖晓1,2

1 中南大学有色金属成矿预测与地质环境监测教育部重点实验室， 长沙 410083 2 中南大学地球科学与信息物理学院, 长沙 410083

适用于近地表(2000 m以内)勘探的频率域电磁法主要有音频大地电磁法(audio-frequency magnetotellurics, AMT), 无线电大地电磁法(radio-magnetotellurics, RMT), 可控源音频大地电磁法(controlled source audio-frequency magnetotellurics, CSAMT)，广域电磁法(Wide Field Electromagnetic Method, WFEM).本文拟从最新的数据采集技术、数据处理技术、正反演算法、实例等四个方面，论述适用于浅部勘探的AMT, RMT, CSAMT和WFEM方法的国内外最新进展，总结目前AMT, RMT, CSAMT和WFEM方法遇到的困难，对潜在的发展方向提出建议.综述表明: (1) 张量测量、多站阵列、多站叠加可提高AMT、RMT和 CSAMT数据的质量.利用近区数据WFEM法可获得良好的效果.国产与国外仪器在质量方面的差距正在逐步缩小.(2)数学形态滤波技术、Hilbert-Huang变换等可有效分离出有用的数据，局部畸变仍然是亟待解决的难题，需要更为深入的研究.(3)矢量有限元与非结构网格的出现大幅度提高了有限元处理复杂电磁问题模拟的精度与应用范围，成为目前电磁正演的首选工具.完全非线性反演算法仍然局限于1D、2D问题，共轭梯度法和高斯牛顿算法等为解决3D问题的发展趋势.地质约束的引入和多数据联合反演可以减小反演的非唯一性.各向异性的反演为目前反演研究的热点之一.(4)野外数据解释的正确性严重依赖于对地下结构先期的维性判别，在2D特性不明显、3D特性明显时，需要采用3D进行反演解释.

近地表勘探； 频率域电磁法； AMT； RMT； CSAMT； WFEM

1 引言

随着人们对周围生活环境认识的进一步加强，以及对矿产资源需求的进一步提高，要求更为可靠的探索地下浅部结构的地球物理勘探方法.适用于浅部勘探的电磁勘探方法主要有音频大地电磁法(AMT)，射线大地电磁法(RMT)，可控源音频大地电磁法(CSAMT)，广域电磁法(WFEM).AMT和RMT的场源分别对应于磁暴和雷电现象、潜艇信号.由于距离足够远，磁暴、雷电和潜艇天线产生的电磁波可近似为平面波.CSAMT的场源为人工电偶极子或者磁偶极子，数据采集一般在远区，场源可近似为平面波.因此，AMT, RMT和CSAMT 可归纳为基于平面波场源的电磁勘探方法.WFEM的场源与CSAMT类似，但测量不局限于远区.

AMT, RMT，CSAMT和WFEM数据采集的频率范围略有不同.AMT的工作频率一般为0.1 Hz～100 kHz; RMT的工作频率一般为10 kHz～250 kHz; CSAMT和WFEM的工作频率一般为0.1 Hz～10 kHz.在地表，我们一般采集随时间变化的电磁场信号E(t)和H(t)(t为时间变量)，通过信号处理获得频率域电磁场E(ω)和H(ω)(ω为频率变量).电磁场信号一般为地下电导率(σ)的函数，电场与磁场的比值Z(ω,σ)=E(ω)/H(ω)(通常称Z为阻抗)建立了频率与地下电性结构的关系.利用地表采集的阻抗Z，反演可获得地下电导率分布.基于广域电阻率概念的广域电磁法在地质勘探中获得了越来越多的成功应用.

本文拟从数据采集和处理技术、反演算法和实例等四个方面来论述浅部勘探AMT，RMT, CSAMT和WFEM方法的国内外最新进展，给出AMT，RMT, CSAMT和WFEM勘探方法目前遇到的困难，并指明潜在的发展方向.

2 数据采集技术

数据采集技术的发展主要体现在数据采集方案和硬件设备两方面.

2.1 采集方案

AMT, RMT和CSAMT的一个共同点为在源的远区进行数据采集.在远区，入射源场可以近似为平面波.远区可采集的数据为水平电场、水平磁场和垂直磁场.由于空气的电导率一般为0，地表的垂直电场分量为0，因此在频率域电磁法一般不采集地表下的垂直电场.如果测站分布设计相对较密，测点距较小，高密度的数据足以保证较高分辨率模型的获取，用于标识地下横向电性变化的垂直磁场的测量也可省略.

由于天然场源信号弱，极化方向随机，极易受各类噪声干扰，这些特征使得高质量AMT数据的获取极为困难.为提高数据质量，合理的设计采集方案是首要任务.在天然源电磁法观测方案的发展历程中，有三个关键节点值得注意.一是张量观测方案的提出(Sims et al., 1971)，通过定义水平电场与磁场分量的二阶阻抗张量来估计地下电性分布.该方案使得天然场的观测真正走向实用，其典型的采集装置如图1所示.二是远参考法(Gamble et al., 1979)的提出，通过在噪声较低的区域布置参考测站，有效压制了测区的噪声干扰，改善了数据质量.该方案自提出后即成为天然场源特别是低频信号观测的标准程序.三是电磁阵列剖面(Electromagnetic Array Profiling，EMAP)(Torres-Verdín and Bostick, 1992)观测的提出，为压制局部异常体对观测数据的畸变影响提供了解决思路.该方案及其处理程序也成为2D电磁剖面处理中重要的步骤.学者们现已将其扩展至三维空间观测层面，如小面元(何继善等, 2010c)、多站叠加(Jiang and Xu, 2013)等观测方式.

人工源电磁法(CSAMT/RMT)由于源的引入提高了数据信噪比，且由于场源极化方向固定，使得矢量和标量观测两种方案均可使用.实际施工中，为提高生产效率，CSAET成为一种常用的观测方案(用一个场源在一个方向上只做电场观测的标量方案).几种典型的观测方案如图2所示.

然而，CSAET等观测方案显然并不适用于地质条件复杂的地区.针对此，学者们提出了许多改进方案，这些改进主要体现在发送端.综合来看，可分为以下几个方面.一是改进信号源的发送形式，如人工源极低频电磁波技术(赵国泽等，2010; 卓贤军等，2011; 卓贤军和陆建勋，2010)，在高电阻率地区建立一个固定的大功率发射台，用人工方法发射0.1～300 Hz超低/极低频电磁信号.一些学者讨论了考虑电离层的影响时该方法的响应(底青云等,2008; 付长民等,2012; 陈小斌和赵国泽,2009; 李帝铨等,2011; 徐志锋和吴小平,2010).二是改进发送信号的编码形式，主要以何继善(2010c)提出的伪随机信号编码为代表，罗维斌等(2012)研究了逆重复M序列伪随机信号编码方式.三是改进发送源的布设方法，如“L”型发射源(王显祥等,2014)、十字型源(孟庆奎,2013)以及多偶极发射装置(雷达等,2014)等.

图1 张量观测方案(Christopherson, 2012; Ren, 2012)Fig.1 Configuration for tensor measurements (Christopherson, 2012; Ren, 2012)

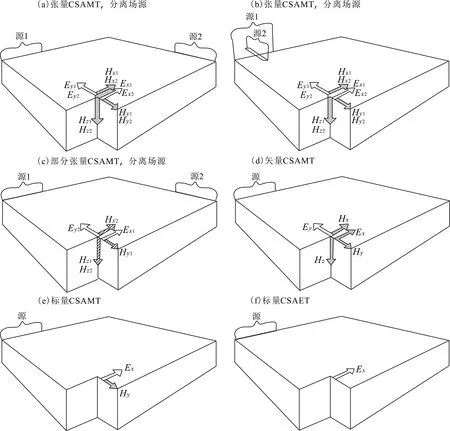
图2 CSAMT法的张量、矢量和标量观测方案(汤井田和何继善，2005)(a)(b)用两个场源，且每个场源做5次的全张量测量； (c)每个场源观测3个分量的部分张量测量； (d)单一场源5次观测的矢量测量；(e)单一场源2次观测的标量测量；(f)用一个场源在一个方向上只做电场观测的标量CSAET法，在少量点上测磁场用以把电场数据转换为近似的电阻率.Fig.2 The configuration of CSAMT tensor, vector and scalar measurements (Tang and He, 2005)(a) and (b) Two sources, a set of five tensor data is measured for each source. (c) A set of three tensor data is measured for each source. (d) A set of five vector data is measured for each source. (e) A set of two scalar data is measured for each source. (f) Only the electric data is measured along the profile for one source. At several measurement sites, the magnetic field is also used to transfer the measured electric field to the apparent resistivity.

值得一提的是，何继善(2010a，2010b)提出了一种新的频率域方法，即广域电磁法(WFEM).广域电磁法具有独特的观测方式，其仅仅测量单分量电场，避免了磁场干扰对测量数据的影响.另外，在发送端采用伪随机信号编码，并且可同时发送包含多频率的信号，提高发送效率；在接收端，进行单分量阵列观测，同时接收多个频率的地电响应信号，提高精度和速度.

2.2 仪器设备

电磁场观测设备分为发送端与接收端两大部分，对于天然场源电磁法，发送端部分可省略.发送端主要包括发电机、逆变器及信号发送控制器等组成部分，接收端主要包括电极、磁场传感器、GPS、电源、信号放大器及采集控制器等组成部分.随着技术的进步，仪器设备也在不断更新换代.综合来看，未来电磁勘探的观测技术及仪器设备的趋势主要为以下几个方面：

(1)采集系统的集成化，实现一套系统的多种电磁数据采集.如加拿大凤凰公司推出的V-8系统，可以进行AMT/CSAMT方法观测；美国Zonge公司的GDP-32II系统，可以进行AMT/CSAMT/观测；德国Metronix公司的GMS-07e系统，可以进行AMT/CSAMT/RMT观测等.

(2)全三维采集，数据记录由单测线的剖面测量逐步转变为全空间阵列三维采集；如Geometrics 公司的Geode EM 3D系统支持3D网络式布设，最多可测量240道数据；Quantec Geoscience公司的Orion 3D系统支持开展全3D勘探等.

(3)频率范围的拓展，更高精度的传感器使得采集频率得以向更低和更高的范围拓展.德国Metronix公司的GMS-07e系统测量频带可达0.00001 Hz～250 kHz；美国Zonge公司的GDP-32II系统测量频带范围可达0.000121 Hz～8 kHz.此外，更大的发送电流、更加轻便的装备、更加持久的续航能力以及更加快捷的实时处理能力也是仪器发展一直努力的目标.

与国外相对成熟的商业仪器相比，国内电磁法仪器的发展相对滞后，主要停留在试验阶段.我国多个科研单位和高校进行了频率域电磁法仪器的研制，如吉林大学(程德福等，2004)、中国地质科学院物化探研究所(林品荣等，2007，2010)、中国科学院地质与地球物理研究所(底青云等，2013; 真齐辉等，2013).

基于全区视电阻率概念(汤井田和何继善, 1994a)， 中南大学成功研制出了JSGY-2广域电磁仪(何继善, 2010c)，其工作频率范围为3/256 Hz～8192 Hz.该仪器可在远区至近区的广大区域进行观测，拓展了观测范围.JSGY-2广域电磁仪已经广泛应用于油气藏、页岩气、地热、煤田采空区、金属矿、水资源等探测领域.因此，国产与国外仪器在质量方面的差距正在逐步缩小，差距主要体现在制造标准、工艺水平和商业化水平等方面.

3 数据处理技术

3.1 天然场源AMT方法

AMT方法的场源为天然雷电，记录的数据为不同采样率的时间域信号.为获得可解释的阻抗视电阻率及相位，需要进行时间域数据处理、时频转换、阻抗估计及局部畸变校正等几个步骤.提高数据质量的努力也主要从这四个方面展开.

3.1.1 时间域数据处理

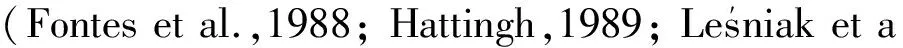
对于时间域数据处理，无论是数据删选还是信噪分离，信噪识别是成败关键.Weckmann 等(2005)提出可利用能量、阻抗在复平面上的分布、阻抗估计误差、相干度和极化方向等多种参数进行综合判断.汤井田等(2012b)指出，强干扰数据的时间域特征为幅值大，形态规则.Escalas等(2013)使用小波分析了天然场源和人工源不同的时频域极化特征，并利用其差异进行信噪识别.

3.1.2 时频转换

时频转换是将时间域信号转换到频率域的过程.快速傅里叶变换(Fast Fourier Transform，FFT)(Cooley and Tukey,1965; Cooley et al.,1969)是最为常用的方法，其优点是计算稳定，易于实现，因此已成为天然场源电磁法数据处理的经典程序之一.但它也存在明显的不足，如时窗函数固定、对信号时间定位能力差、频率混淆效应与泄露效应无法根除等，因此，一些不同的谱估计方法相继被引入电磁数据的处理中，如高阶统计(王书明和王家映,2004)、最大熵谱分析法(Tzanis and Beamish,1989)、S变换(陈海燕等,2012;景建恩等,2012)等.这些方法对于特定问题表现出了优于FFT的性能，但尚未成为标准处理程序.小波变换是一种具有多分辨率、多尺度的数学方法，具有良好的时频局域性和自适应性，可对信号的不同频率成分进行分析，在信号处理领域已多有应用，众多学者研究了其对电磁数据的处理效果(Zhang and Paulson,1997; 何兰芳等,1999; 徐义贤和王家映,2000;Trad and Travassos,2000; 刘宏等,2004;严家斌和刘贵忠,2007)，证明了其有效性，但该方法依赖于小波基函数的选取，这也成为其难点.天然电磁场信号是非线性、非平稳信号(Chant and Hastie,1992)，噪声同样常具非平稳性(Banks,1998)，因此，非线性、非平稳信号分析工具是最佳选择.汤井田等(2008)将Hilbert-Huang变换引入电磁数据处理中，基于经验模态分解(Empirical Mode Decomposition, EMD)与希尔伯特谱分析，对大地电磁数据进行处理，证明了该方法的有效性，其后该方法被进一步完善和推广(Cai et al.,2009; Chen et al.,2010; Cai,2013，2014; Neukirch and Garcia,2014)，显示出良好的应用前景(见图3).

3.1.3 阻抗估计

张量阻抗估计是获取高质量转换函数、阻抗视电阻率及相位等解释参数的重要步骤.针对不同的噪声类型、含噪程度，主要的张量阻抗估计方法经历了从最小二乘估计到稳健阻抗估计，从引入单参考道到多道数据的利用等阶段.

最小二乘(Sims et al.,1971)是估计阻抗张量的经典方法.在噪声环境相对平静或以随机噪声为主的地区，该方法是有效的，但是当存在有色噪声或相关噪声时，最小二乘估计结果往往会出现严重偏离.如何在含噪情况下获取高质量的频域阻抗参数成为电磁研究者们关心的问题.

稳健阻抗估计是一种主流的提高阻抗估计质量的方法. 各种稳健阻抗估计都是通过自适应地赋权来降低奇异值在阻抗估计中的地位.一般来说，稳健估计的成功依赖于整个数据段中性态良好的数据占主要地位，当噪声贯穿大部分甚至整个观测时段时，稳健估计方法就失效了(Egbert and Booker,1986; Chave et al. ,1987; Chave and Thomson,1989; Egbert and Livelybrooks,1996; Chave and Thomson,2003; Smirnov,2003).Jones等(1989)、Sutarno(2008)及汤井田等(2013a)分别对稳健阻抗估计方法进行了综述和对比.

图3 HHT矫正振动干扰的实例(汤井田等，2008)(a) Hx的EMD 分解残差; (b) Hx原始信号; (c) 振动干扰矫正后的Hx信号. Fig.3 A field example of the vibration interference which is corrected by the HHT method (Tang et al., 2008)(a) EMD decomposition of the Hx component; (b) The original Hx signal; (c) The corrected Hx signal.

远参考道估计是提高阻抗估计质量的另一种可靠方法.自Gamble 等(1979)首次提出远参考方法以来，该方法已成为天然场源电磁法的标准程序，并取得了长足的发展.利用测点磁场与参考点磁场之间的相关性，可以实现含噪数据的剔选(Ritter et al.,1998; Varentsov,2006; Sokolova et al.,2005).Larsen等(1996)提出了利用参考道实现信噪分离的思路，当远参道中不含噪声时，可以估计出测站磁场中的天然场信号项，进而获得平面波阻抗的估计.Oettinger 等 (2001)进一步证明，当参考道中含噪时，引入第二个远参考道可以得到无偏的平面波阻抗估计.

多道数据的利用是学者们努力的方向之一. 利用测站间电磁场分量的相互关系对含噪时段数据进行预测是一种常见的思路，如大地电流-大地电磁(Telluric-Magnetotelluric，T-MT)方案(García and Jones, 2005)， “伪远参考”(Muoz and Ritter,2013)及组合站间转换函数(Estimation of Local transfer-functions by Combining Interstation Transfer-functions，ELICIT)(Campanyà et al., 2014)等一批基于测站间“转换函数”的采集处理方案.这些方案不仅改善了MT的数据质量，而且拓展了数据采集的思路.然而，参考道的数据质量决定了此类方法的适用范围，另一些学者提出了算法方面的改进，如Kappler (2012)提出了IARWR(Intersite Activity Ratio Wiener-filter Replacement)时间域去噪方法.王辉等(2014) 提出利用多道同步依赖关系进行阻抗估计的方法，Cui 等(2013)引入独立分量分析(Independent Component Analysis，ICA)的方法，Varentsov 等(2003)提出利用多道远参考联合使用的方法，另外，Egbert和Booker(1989)、Egbert(1997，2002)系统阐述了利用阵列数据进行信噪分离的阻抗估计方法，在其基础上，Smirnov 和Egbert (2012)发展了阵列数据的主成分分析稳健估计方法(Principal Component Analysis，PCA).

此外，利用多频点数据进行光滑处理也是提高数据质量的有效手段之一.如利用视电阻率、相位数据的转换关系(Weidelt,1972)，可以实现阻抗相位参数对畸变视电阻率曲线的校正(杨生等,2001).Parker提出的Dplus及Rhoplus反演方法(Parker,1980; Parker et al.,1981; Parker et al.,1996)是这类处理的优秀代表.该方法考虑了阻抗视电阻率、相位数据的关联性以及数据在频率域的连续性，其拟合数据来自于所谓D+或R+模型的响应，具有明确的物理意义，在频域数据的一维分析与拟合中应用广泛(Beamish and Travassos,1992; Fischer and Weibel,1991; Spratt et al.,2005).

3.1.4 局部畸变校正

当地表存在三维局部电性不均匀体时，会因积累电荷而使测量电场产生局部畸变，进而影响计算所得的阻抗数据.这种局部畸变的影响表现在两个方面(Bahr,1988,1991; Berdichevsky and Dimitriev,1976)：一是电流型畸变(galvanic distortion)，以准静态形式影响观测的电场，使阻抗视电阻率数据在所有频点上产生所谓“静态位移”，或称为“静态效应”；二是感应型畸变(inductive distortion)，会同时影响阻抗视电阻率、相位数据.对于实测数据而言，局部畸变往往是不可避免的，即使是信噪比很高的人工源电磁法数据，因此，对于局部畸变的校正研究引起了学者们的极大兴趣. 阻抗张量分解技术将观测值视为区域阻抗与局部畸变两部分，具有较为清晰的理论基础，主要的分解算法有Swift 方法(Swift,1967)、Bahr分解( Bahr,1988; Bahr,1991; Prácser and Szarka,1999)、GB 分解(Groom and Bailey,1989,1991; Jones and Groom,1993)、Chave-Smith电磁场全畸变分解法(Chave and Smith, 1994; Chave et al., 2004)、多测点-多频点分解方法(陈小斌等,2014; McNeice and Jones,2001)以及相位张量分解(Caldwell et al.,2004; Weaver et al.,2006; Booker,2014)等. 针对静态效应问题，除了上述阻抗张量分解方法外，还发展了一系列校正方法， 这些方法可归为三大类，即利用相位或磁场分量测量结果(阎述和陈明生,1996)、利用空间域(Torres-Verdín and Bostick,1992)或波数域(宋守根等,1995)数字滤波方法和联合反演方法(Sternberg et al.,1988)等.

值得指出，目前实际应用较多的局部畸变校正方法主要为阻抗张量分解与空间滤波算法.

3.2 人工源电磁法

CSAMT、WFEM和RMT为人工源电磁法，其处理方式与AMT法有许多相似之处，但也存在明显的差异，如发射信号可以固定在特定的频率或组合频率，提高该频率的信号能量，在接收端可以获得很高的信噪比，进而得到高质量的数据，同时因场源极化方向固定，在不同的空间位置不同方向上的信号能量差异巨大，当采集区域限制在特定范围内时，可以简化观测方案及波阻抗的计算方法.与天然场源方法相比较，人工源电磁法的数据处理较为简单，但因为源的引入，也产生了一系列与源有关的问题(何继善，1991; 汤井田和何继善，2005; 高文，1991).

非平面波效应是人工场源效应之一，其主要特征是会造成所谓“过渡区”和“近区”卡尼亚视电阻率、相位数据畸变.对此，首先需要讨论人工源条件下，观测场区的划分问题.何继善(1991)、汤井田和何继善(2005)对这一问题进行了详细的论述，指出场区的划分与地下电阻率、观测频率以及发收距等相关，可用综合参数“电距离”来进行衡量.岳瑞永和徐义贤(2004)、陈明生和闫述(2005)、林威(2009)、程辉和李帝铨(2014)分别给出了不同的定量场区划分方法，为畸变数据的识别提供了依据.

在过渡区及近区，卡尼亚视电阻率及相位的畸变常常会带来错误的认识，通过定义适当的电阻率参数以合理利用过渡区数据是应对措施之一，如Das(1995)、曹昌祺(1978)、黄皓平和朴化荣(1992)、殷长春和朴化荣(1991)、詹少全等(2011)以及冯兵等(2013)均做过不同的尝试.实际工作中，合理设计采集方案，尽量保证数据处于远区是避免非平面波效应影响的最佳策略.汤井田等(2013b)、王若等(2004)讨论了不同条件下适宜的观测方案. 陈卫营和薛国强(2014)则给出了适用于全场域的有效趋肤深度快速估算公式.

阴影和场源附加效应是另一类由场源所引起的问题. 目前对该问题的研究多处于数值模拟阶段(Boschetto and Hohmann,1991;闫述和陈明生,2004; 王若等,2009; 汤井田等,2012c).陈明生和闫述(2005)通过实例表明，阴影和场源附加效应是由地层波所携带的源与观测点之间、源下方真实地质情况的信息决定，是可以加以利用的.有效的阴影和场源附加效应的处理方案仍有待后续研究，是今后的一个研究方向.

汤井田和何继善(1993，1994a，1994b)从电磁场统一的角度，系统地讨论了频率电磁测深中几种等效全区视电阻率的原理、定义和具体算法，并提出形式更为简洁的Ey视电阻率(汤井田等，2011).基于等效全区视电阻率概念(汤井田和何继善, 1994a)的WFEM法，可不局限于远区，从而拓展了观测范围.基于单分量的测量， 广域电磁法有效压制电磁场干扰对测量数据的影响，从而提高抗干扰能力.

4 正反演算法发展

4.1 正演

数值模拟方法具有普遍适用性，不仅仅适用于本论文研究的 AMT，RMT, CSAMT和WFEM问题，还适用于其他问题，如MT，CSEM, 直流电法等.为了更好地为读者叙述数值模拟技术的发展趋势，下面的阐述着眼于其在整个地电磁场模拟的发展.通常，数值模拟方法可分为四类：体积积分法(Raiche, 1974; Hohmann, 1975; Weidelt, 1975; Avdeev et al., 2002; Zhdanov et al., 2006)，边界积分法(Parry and Ward, 1971; Doherty, 1988; Liu and Becker, 1992; Xu et al., 1997; Liu and Lamontagne, 1998; Ren et al., 2012)，有限差分法(Mackie et al., 1994; Aprea et al., 1997; Smith, 1996; Haber et al., 2000; Newman and Alumbaugh, 2002; Hou et al., 2006; Streich, 2009)和有限单元法(Badea et al., 2001; Mitsuhata and Uchida, 2004; Key and Weiss, 2006; Nam et al., 2007).对于有限差分、体积分方程法的优缺点，请查看已有的综述文章Avdeev (2005), Böerner (2010) 和Everett(2011).需要特别提出的，Penz等(2013)提出了利用有限差分解决复杂地电模型的新思路，扩展了传统有限差分的应用范围. 本节只阐述适用于任意复杂模型的有限单元法.

从Coggon(1971)首次将有限单元法应用到电磁模拟以来，该领域有了突飞猛进的发展，技术的进步可大概归纳为微分控制方程、有限元空间、网格离散化技术、线性求解器等四个方面.电磁模拟可基于电场方程(Nam et al., 2007; Farquharson and Miensopust, 2011)、磁场方程(Siripunvaraporn et al., 2002;Franke et al., 2008)和不同种类的势场方程. 对于低频问题，由于空气的电导率为0，磁场方程在空气中未定义.因此，磁场方程一般很少用于求解低频地球物理电磁场问题.低频情况下，电场方程在空气中变得非常的病态，从而导致高条件数的离散系统矩阵.高条件数一方面降低了求解的精度，另外一方面增加了迭代求解器的迭代次数，从而增加了求解时间.常用的势场方程包含H-Ω式，A-Ω式 (Haber et al., 2000; Badea et al., 2001)和T-Ω式(Mitsuhata and Uchida, 2004).势场方程导致的离散系统矩阵的条件数一般较低，从而降低了对求解器的要求, 在处理电导率不连续界面上的边界条件时，势场方程存在一定的复杂性.

有限元空间常常包含节点型基函数和向量基函数(Nédélec, 1986; Farquharson and Miensopust, 2011).节点型基函数构成连续的有限元空间,要求电场或者磁场在地下为连续函数.在电性不连续界面，如电导率跳跃界面处，电场在跳跃界面的法向分量不连续.因此节点型基函数构造出的电磁场有限元解，强加了法向连续性条件，从而使得有限元解不准确，或者偏离真实解.向量基函数可解决节点型基函数产生的上述问题. 向量基函数构造的有限元解只要求电场的切向连续性，保留电场的法向不连续性；另外一方面，能够保证单元内场的散度为零.因此，向量基函数构造的有限元解不存在伪解.由于其优越的性能，向量基函数已逐步代替节点型基函数,成为地球物理电磁场数值模拟的标准方式.

网格离散化技术经历了从结构化网格到非结构化网格的过渡(Key and Weiss, 2006; Franke et al., 2008).早期的电磁场模拟一般采用简单的结构化网格，如四边形、六面体.随着研究的深入，人们探究复杂地电磁场模型欲望的加强，结构化网格的缺点越来越突出.结构化网格很难真实地模拟复杂的地下结构，如任意复杂的地形情况. 随着计算几何技术的突飞猛进，产生了非常快速、可靠地用三角形和四面体来任意精确逼近复杂地电模型的技术. 有限元本身对单元类型没有要求，自然地，基于三角形与四面体的非结构化网格越来越多地应用于地电磁场的有限元模拟. 非结构化网格能够非常容易地实现网格的自适应加密，因此，非结构化有限元模拟越来越重视网格自适应加密技术，生成高精度的数值结果.典型的应用为： Key和Weiss (2006)应用自适应三角形网格研究了复杂的2D 大地电磁问题. Li和Key (2007)应用自适应三角形网格研究了复杂的2D 海洋CSEM问题(图4). Ren 和Tang(2010)应用自适应四面体网格研究了3D DC问题. Schwarzbach等(2011)应用自适应四面体网格研究了3D CSEM问题.Ren等(2013) 应用自适应四面体网格研究了3D MT和RMT 问题(图5).目前, 非结构网格在有限元模拟中逐渐成为主流.

线性求解器方面也展现出较大的进步. 电磁场问题经有限元离散化后生成大规模的稀疏矩阵.由于计算机内存的限制以及直接法的落后，早期的研究者一般采用迭代法来完成线性方程组的求解.然而，求解低频电磁场问题时，线性方程的条件数往往较大，导致过多的迭代求解步骤，从而增加了计算时间.因此，如何设计低成本、高效的迭代预处理器成为了迭代法的发展方向.值得提及的是，Grayver 和Burg (2014)提出了一种基于辅助空间的高效预处理，能够有效地减小迭代次数.目前，直接求解器方面获得了非常大的突破，产生了有效的直接法求解器，如基于LU矩阵分解法和OpenMP的PARDISO求解器(Schenk和Gärtner, 2004)，基于波前法和MPI的MUMPS求解器(Amestoy et al., 2002).Streich (2009)测试了MUMPS求解器的优越性能，求解了超过百万未知数的大型地电磁场问题.地电问题一般为多源问题，即含多个右端项.直接法能够快速地处理多个右端项问题，因此获得了越来越多的重视，有逐步取代迭代求解器的发展趋势.另外为了求解超大规模的问题，基于MPI并行的求解技术也获得了大量的尝试和应用.Puzyrev 等(2013) 利用区域分解和MPI求解了大规模的CSEM 3D 问题(见图6)；Ren等(2014)成功应用了一种新的FEDI-DP区域分解技术计算了大规模MT问题.

4.2 反演

反演算法是一个优化过程，目前常用的反演算法可归纳为两类：非线性反演算法和线性迭代算法.

非线性反演算法包括人工神经网格法、模拟退火法、蒙特卡罗法等.非线性反演算法最大的优点是可避开局部极大、极小值，搜索出全局最优模型.然而，非线性反演算法需要大量的样本，根据每个样本的测试结果，进行有方向性的样本筛选或样本升级，搜索出符合野外实测数据的样本. 在模型搜索过程中，需要大量的正演计算，由于每一次正演需要消耗大量的计算时间，非线性反演算法目前仅仅适合1D或者小规模2D反演问题.

线性迭代算法主要包括高斯-牛顿算法及其变种、共轭梯度算法及其变种.高斯-牛顿算法及其变种是目前流行的反演方法，广泛应用于MT反演、CSEM反演、DC反演等.灵敏度矩阵是制约反演速度的关键因素，由于灵敏度矩阵是密实矩阵，对于3D大规模问题，计算和存储灵敏度矩阵是困难的.共轭梯度算法及其变种通过减小目标函数梯度来达到反演收敛的目的，由于不需要引入灵敏度矩阵，共轭梯度算法及其变种的计算消耗相对小.关于反演算法在地球物理电磁法的应用，请查看已有的综述文章Avdeev (2005), Böerner (2010) 和Everett(2011).

总体来说，对于2D和3D问题，可行的反演算法为线性迭代算法.由于上述最优化问题求解技术发展已经相当成熟，地球物理学者往往关注如何提高迭代中的正演计算效率，因此4.1节阐述的正演算法的发展，直接促进了反演计算的效率和发展.

图4 2D 海洋 CSEM问题的非结构化三角形网格的自适应加密 (Li and Key, 2007)Fig.4 Adaptive refinements for 2D marine CSEM problems with triangles (Li and Key, 2007)

图5 RMT问题中三维梯形模型的非结构化四面体网格的自适应加密，为单元误差(Ren et al., 2013)Fig.5 Adaptive refinements for 3D RMT problems with tetrahedral elements (Ren et al., 2013)

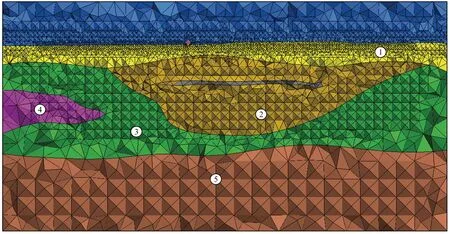
图6 基于区域分解的大型CSEM 3D 问题的MPI计算， 不同颜色代表不同的子区域，最上蓝色为空气区域，网格包含2.8 百万个四面体，16CPU上计算时间为1.5 min (Puzyrev et al., 2013)Fig.6 Large-scale parallel computation with MPI. The grid contains 2.8 millions elements, with a run-time of 1.5 minutes using 16 CPUs (Puzyrev et al., 2013)

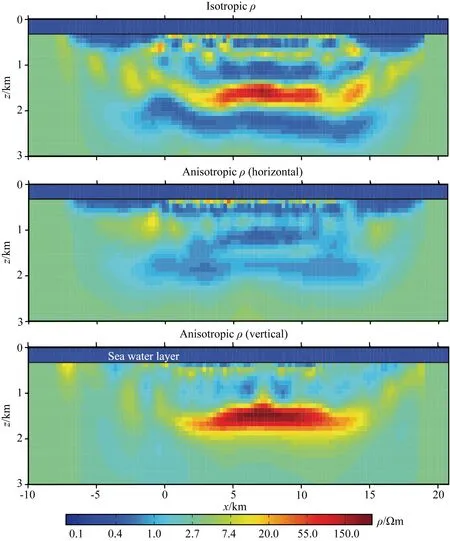
图7 CSEM各向异性3-D反演结果图(Newman et al., 2010)Fig.7 Inversion results for CSEM anisotropic problems (Newman et al., 2010)

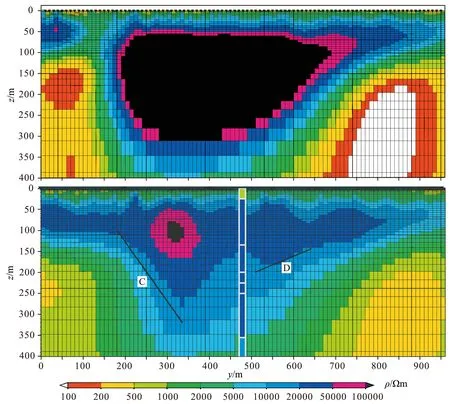
图8 2D RMT反演结果，顶图忽略位移电流造成了错误的高阻区域.底图未忽略位移电流，结果与测井结果吻合 (Kalscheuer et al., 2008)Fig.8 2D RMT inversion results. The top figure shows the case of ignoring the displacements which leads to an incorrect highly resistive area. The bottom figure shows that when considering the displacement currents, the inverted result agrees well with logging results (Kalscheuer et al., 2008)

图9 巴西米纳斯吉拉斯州xxx测线二维反演结果图(Terra and Menezes, 2012)Fig.9 2D inversion results from an AMT profile in the Minas Gerais State of Brazil (Terra and Menezes, 2012)

反演多解性促进了联合反演的发展，因为联合反演可减低结果的多解性，提高结果的精度和可靠性. Hu等(2009)发表了2.5D频率域电磁反演和2D地震联合反演；Candansayar 和Tezkan(2008)采用最小二乘法进行了RMT和DC的2D联合反演；Bala和Pieta(2010)采用蒙特卡罗法进行了相似的1D DC/AMT联合反演.另外，随着计算资源的大幅度提高，各向异性的反演越来越成为一种研究热点，例如Newman等(2010)进行了CSEM数据各向异性3D反演(见图7).

位移电流在RMT反演过程中的应用越来越得到重视.在高阻环境和高频率情况下，位移电流并不远远小于传导电流.对于浅地表问题，特别是在地形起伏严重的区域，位移电流应该考虑在反演过程中，忽略位移电流会造成反演结果错误.比如，Kalscheuer等(2008)详细地分析了位移电流在RMT反演中的重要性，给出了忽略位移电流会造成反演结果的不合理性(见图8).

另外，超级计算机促使了反演的工业化实现.高性能计算平台的发展经历了单核到多核，再到近年来的GPU.Alumbaugh等(1996)、Alumbaugh和Newman(1997), Newman和Alumbaugh (1997, 1999)首先将高性能计算平台应用在大规模电磁计算中，完成了真实的3D地质模型的电磁模拟.Commer和Newman(2008)、Newman等(2010)采用了32768个CPU进行了3D CSEM数据成像的大规模并行计算，计算时间为几天，奠定了大规模的3D电磁问题成像计算在工业中应用的基础.Weiss和Schultz (2011)提供了使用单一GPU进行大规模电磁数据模拟的可行性研究.

5 实例应用

随着数据采集技术、信号处理技术、正反演算法的快速发展，频率域电磁法得到了人们越来越多的关注，其应用范围越来越宽广.由于其信号频率范围的特性，上述三类频率域电磁法主要应用于矿产资源勘探、地热资源或地下水勘探、环境与工程地球物理等浅部地球物理问题.

5.1 矿产资源

随着我国国民经济的快速发展，各种矿产资源的需求量越来越大．近年来，面对矿产资源的日益枯竭，开展中深部(大于500 m)找矿迫在眉睫(夏时斌等，2012).最新的成矿理论研究和深部定位预测验证结果均表明，地下500～1500 m深度见矿范例众多，表明大陆深部蕴藏着潜力巨大的矿产资源(叶益信等，2011)，因此如何准确、有效地开展中深部和各类隐伏区的探矿找矿，已成为现阶段及未来的重大研究任务.

音频大地电磁法和可控源音频大地电磁法已逐步应用在隐伏矿及深部矿的勘察中，并取得了不错的效果(Sheard et al., 2005；Zhdanov, 2010；Vallée et al., 2011；Smith, 2014).在AMT和CSAMT两种方法中，AMT为天然场源，抗干扰能力差，但其装备简便，易于操作，适合在地形复杂，干扰相对较小的地区开展勘察；而CSAMT采用人工源，信号强，抗干扰能力大，但源的布设及采集较为复杂，适用于地形简单但干扰相对较大的地区.

AMT和CSAMT受高阻屏蔽作用小，对低阻体反映灵敏.图9给出了一个典型的AMT勘探低阻角砾云母橄榄岩的实例(La Terra and Menezes, 2012)，角砾云母橄榄岩是原生金刚石的成矿标志，而其电性特征表现为低阻.针对AMT死频带问题，La Terra等人采用发射天线，在距测点四倍趋肤深度外发射人工信号，以此提高频带信噪比及数据质量.对AMT数据进行了可靠的数据处理，并获得了各个测线的二维反演结果.为进一步验证二维反演结果的可靠性，利用WSINV3DMT程序(Siripunvaraporn and Sarakorn 2011)，作者以二维反演结果为初始模型，进行了3D反演(图9b).三维反演结果与二维反演结果的一致性验证了反演结果的可靠.

近年来，广域电磁法以其探测深度大，分辨率高，抗干扰能力强、仪器轻便、观测速度快，勘探范围大等特点，在深部资源勘探中发挥着越来越重要的作用. 胡艳芳和何继善(2015)在安徽铜陵地区开展了强干扰矿区广域电磁法的有效性试验，为保证数据采集的质量，进行了强干扰区最佳发射电流的试验研究(电流从100～10 A),结果表明当发射电流大于20 A时，数据信噪比才能得以保证. 图10为铜陵强干扰矿区某测线2D反演结果，可以看出矿区地层的似层状体现非常明显，矿体横向和深度范围内出现了低阻异常，并识别出了两条断层，与已知钻孔信息一致.经地质、物探等综合信息，推断2号异常区还存在成矿的空间，该处低阻异常为矿体或矿化引起.

5.2 地热资源或地下水勘探

地热资源是集“热、矿、水”三位一体的清洁可再生能源，目前已被广泛应用于取暖空调、生活热水、医疗等许多领域，具有巨大的开发前景(周厚芳等，2004；黄力军等，2004；廖忠礼等，2006).

地热资源一般位于充满流体的断层或裂缝中，这些流体富含盐分，具有良好的导电性，相对围岩表现为低阻特性，这些特征使得电法及电磁法在地热资源的勘探中应用效果显著.一般地热资源主要分为岩浆型与断陷盆地型两种类型，岩浆型地热资源分布范围小，温度高，但是埋深浅，可采用常规直流电阻率法进行勘探. 断陷盆地型地热资源是目前利用最广的地热资源，具有分布广、中低温、埋深大等特点，可利用勘探深度较大的AMT和CSAMT以及MT进行勘探. 对于中浅部地热资源，常选用AMT或CSAMT.

Barcelona等(2013)给出了一个AMT勘探地热资源的实例，为了确定阿根廷西北部地区地下电阻率的分布，圈定出与温泉相关的区域，综合考虑测区的地形、水文、地质及构造等信息，选用AMT法成功进行了地热资源的前期勘探.在该实例中，由于测区位于山区，地形起伏大，区域维性相对比较复杂，所以根据区域与局部的地质特征先确定出可能的地电响应，然后对AMT数据进行了维性分析，分别做了一维和二维反演，综合实际水文、地质等先验信息，二维反演解释结果更为合理可靠，成功获得了地下一定深度内的电阻率分布图.

Fu等(2012)给出了一个CSAMT勘探地下水资源的实例，在北京郊区强干扰条件下成功进行了地下水的勘探工作.在该实例中，为保证强干扰条件下的数据质量，通过加大发射功率、延长偶极子长度、增加测站采集时间等措施来提高数据信噪比；在数据处理时，利用HHT(汤井田等, 2009，蔡剑华等, 2011)进行了信噪分离.图11 给出了1D反演结果及地质解释示意图，通过与已知的实际钻孔资料对比，清晰地查明了高阻石灰石岩层的埋藏深度，并根据含水带低阻特性，成功圈出了地下400～800 m处的含水破碎带.

总的来说，在地热或地下水资源的勘探中，一般常根据测区地形、干扰情况以及地热埋藏深度等实际因素选取合适的电磁方法，对采集的数据进行可靠的数据处理，获得有用的信号.然后，针对测区的地形，进行地形校正，分析采集数据的维性，确定地下水资源的流动方向(走向)，在二维假设成立的情况下，才能够运用二维反演算法.对于二维假设不满足的情况(地下水流动一般呈不规则状态)，三维反演是必要的.

5.3 环境与工程地球物理

环境与工程地球物理，其任务是通过各种高精度的地球物理探测，了解近地表地下空间内的物质分布、运动规律等，从而为各类工程和中浅层资源的设计、施工、检修、维护、开发提供依据.

图10 安徽铜陵强干扰矿区某线广域电磁法二维反演结果P2d，二叠系上统大隆组；T，三叠系；C，石炭系；P2l，二叠系上统龙潭组；P1，二叠系下统地层.Fig.10 2D inversion result in Tongling P2d,Dalong formation of Upper Permian; T, Triassic; C, Carboniferous; P2l, Longtan formation of Upper Permian; P1, formation of Under Permian.

图11 北京郊区某测线CSAMT反演结果及地质解释示意图(Fu et al., 2013)Fig.11 The CSAMT inversion results and its geological interpretation along the profile located on the outskirts of the Beijing city (Fu et al., 2013)

RMT是近20年才逐步发展的一种浅地表地球物理勘探方法(Müller et al., 1994; Tezkan et al., 1996; Tezkan et al., 2000; Tezkan et al., 2005; Bastani, 2001; Bastani et al., 2009; Bastani et al., 2013; Kalscheuer et al., 2008; Ren et al., 2012).RMT 法测量频段为10000 Hz～250 kHz，勘探深度为数米到数十米，目前多应用于浅地表工程、资源勘探及环境监测.在RMT应用中，对于浅地表问题，特别是在起伏地形严重的区域，位移电流应该考虑在反演过程中，不适当地忽略位移电流，会造成反演结果错误(Kalscheuer et al., 2008).

近年来，随着计算机的快速发展，RMT三维反演也已经逐渐应用于实际生产中，并在数据解释方面发挥着重要作用.Newman等(2003)采用RMT法对德国一地下垃圾场是否发生渗漏污染等情况进行了勘探，在该实例中，对RMT数据进行了二维和三维反演结果的对比.结果表明，二维反演结果过高估计了垃圾埋藏深度及范围,得出了错误结论，而三维反演结果能够精确地圈定垃圾坑的边界及深度，判断垃圾坑是否发生渗漏污染(图12).

另一方面，为了压制反演的多解性，进一步提高RMT反演结果的可靠性， RMT与多种方法的联合反演得到了发展和应用.Candansayar和Tezkan(2008)从RMT和DC联合反演的方法原理、合成理论数据以及野外实际数据的联合反演等方面做了详细的介绍，并成功地查明了德国凯尔彭实验基地断层位置约在地下16 m处.文中指出地表浅部的小尺度目标体对RMT数据有较大的影响(易产生静位移)，但单独的RMT反演结果不能分辨出浅地表的小尺度目标体，并增加了反演的多解性.直流电阻率法对地表浅部目标体有很好的反映，因此将RMT联合DC进行反演，不仅清晰查明了地表浅部小尺度目标体以及深部的电性特征，同时极大地减小了反演结果的非唯一性，提高了反演结果模型分辨率，在此次实际勘查中取得了良好的应用效果.

图12 测线反演结果对比图(a)二维反演结果; (b)三维反演结果. 钻孔资料显示垃圾坑基底深度约为13 m (Newman et al., 2003)Fig.12 Comparison of the inversion results(a) 2D inversion result; (b) 3D inversion result. Landfill drilling data show the basement has a depth of 13 meters (Newman et al., 2003)

6 结论

基于目前最新的文献，本文从数据采集技术、信号处理技术、反演算法和实例分析等四个方面分别论述了频率域电磁法的发展现状，主要的结论可概述为：

(1)数据采集与仪器.数据采集方案由单点张量采集向多点同步、多参考道、三维阵列的方向发展，主动源电磁法在信号发送方式、编码方式、场源布设方法以及接收端的观测方案等方面涌现出诸多新尝试，提高了数据采集质量和效率. 随着仪器开发技术的日趋成熟，采集系统已逐步实现多方法集成、全三维采集，元器件精度的提高也使得数据采集频率范围、采集精度及效率等获得了大幅扩展和提高.尤其可喜的是，随着人力与资金的大幅投入，国产仪器与国外仪器在质量方面的差距正在逐步缩小.

(2)数据处理技术方面.由于天然电磁场强度较低，AMT数据的信噪比通常不高.为了获得或者分离出有用的信号，可采用一些新的信噪分离技术，如数学形态滤波技术、Hilbert-Huang变换等.张量阻抗估计经历了从最小二乘估计到稳健阻抗估计，从引入单参考道到多道数据的利用等阶段.局部畸变仍然是亟待解决的难题，目前的主要校正方法为阻抗张量分解、空间滤波及联合反演等.CSAMT和RMT方法由于人工源的引入，信噪比得到大幅提高，其数据处理技术的发展集中在非平面波效应、阴影和场源附加效应的识别与压制等方面.值得提出的是，全区电阻率以及广域电磁法的提出，有效地利用了非远区的数据，为非平面波效应问题的解决提供了途径.

(3)正反演算法方面.为了求解复杂AMT/RMT/CSAMT/WFEM问题，有限元法成为了不可或缺的正演计算技术.为了进一步提高有限单元法的计算精度和效率，基于边的矢量有限元和可以离散任意复杂模型的非结构化网格越来越成为主流.另外，由于直接求解器领域的在求解大型线性方程组的快速发展，对于多源地球物理问题，直接法有取代传统的迭代法的趋势.相对于正演算法的快速发展，由于其非线性，地球物理领域的反演算法本身的发展相对滞后，基本上为对经典的非线性最优化算法的应用，如共轭梯度法、高斯牛顿算法等.由于其超大的计算量，完全非线性反演算法如遗传算法等仍然处于1D、2D问题.与此不同，基于线性化的反演算法，如共轭梯度法、高斯牛顿算法等，3D模型的反演已经变得相对实用.另外，为了提高反演算法的精度，联合反演，如与地震数据等其他地球物理数据的联合反演， 目前正获得越来越多的应用.对于一些简单的问题，电阻率的各向异性的反演也获得了一些重视.RMT问题的频率较高，需要考虑位移电流，为了获得正确的RMT反演结果，必须改正现有的代码，使其包含位移电流项.由于WFEM法出现较晚，需要开发更为可靠的正反演算法.

(4)实际应用.目前上述频率域电磁法在不同的地球物理问题中得到了广泛的应用，如矿产资源勘探、地热或地下水资源勘探、环境与工程地球物理和油气勘探等.由于地下结构可能存在2D、3D特性，在应用反演算法进行数据解释时，需要对地下结构的维性进行正确的判别.在2D特性不明显，或者3D特性明显时，需要采用3D反演算法.另外，即使对于2D特性明显的区域，3D反演不仅可以验证结果，还可以辅助2D反演，获得一些更为精细的局部异常结构.因此，三维采集与反演已逐渐成为主流.此外，为了获得更为可信的反演结果，联合反演的重要性日益明显.

Alumbaugh D L, Newman G A, Prevost L, et al. 1996. Three-dimensional, wideband electromagnetic modeling on massively parallel computers.RadioScience, 31(1): 1-23.

Alumbaugh D L, Newman G A. 1997. Three-dimensional massively parallel electromagnetic inversion-part II. Analysis of a crosswell electromagnetic experiment.GeophysicalJournalInternational, 128(2): 355-363.

Amestoy P R, Duff I S, L′Excellent J Y, et al. 2002. A fully asynchronous multi-frontal solver using distributed dynamic scheduling.SIAMJournalonMatrixAnalysisandApplications, 23(1): 15-41.Aprea C, Booker J R, Torquil Smith J. 1997. The forward problem of electromagnetic induction: accurate finite-difference approximations for two dimensional discrete boundaries with arbitrary geometry.GeophysicalJournalInternational, 129(1): 29-40.Avdeev D B, Kuvshinov A V, Pankratov O V, et al. 2002. Three dimensional induction logging problems, Part I: an integral equation solution and model comparisons.Geophysics, 67(2): 413-426.

Avdeev D B. 2005. Three-dimensional electromagnetic modelling and inversion from theory to application.SurveysinGeophysics, 26(6): 767-799. Badea E A, Everett M E, Newman G A, et al. 2001. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials.Geophysics, 66(3): 786-799.

Bahr K. 1988. Interpretation of the magnetotelluric impedance tensor: regional induction and local telluric distortion.J.Geophys., 62: 119-127.

Bahr K. 1991. Geological noise in magnetotelluric data: a classification of distortion types.PhysicsoftheEarthandPlanetaryInteriors, 66(1-2): 24-38.

Bastani M. 2001. EnviroMT: A new controlled source/radio magnetotelluric system [Ph. D. thesis]. Uppsala: Acta Universitatis Upsaliensis. Bastani M, Malehmir A, Ismail N, et al. 2009. Delineating hydrothermal stockwork copper deposits using controlled-source and radio-magnetotelluric methods: A case study from northeast Iran.Geophysics, 74(5): B167-B181. Bastani M, Persson, L, Beiki M, et al. 2013. A radio magnetotelluric study to evaluate the extents of a limestonequarry in Estonia.GeophysicalProspecting, 61(3): 678-687.Beamish D, Travassos J M. 1992. The use of the D+solution in magnetotelluric interpretation.JournalofAppliedGeophysics, 29(1): 1-19. Berdichevsky M N, Dimitriev V T. 1976. Basic principles of interpretation of magnetotelluric sounding curves. ∥Ada S A ed. Geoelectric and Geothermal Studies, (East-Central Europe, Soviet-Asia), KAPG Geophysical Monograph, Akadémiai Kiadó, Budapest. 165-221. Bielecka M, Danek T, Wojdyla M, et al. 2009. Neural networks application to reduction of train caused distortions in magnetotelluric measurement data.SchedaeInformaticae, 17-18: 75-86.

Böerner R U. 2010. Numerical modelling in geo-electromagnetics: advances and challenges.SurveysinGeophysics, 31(2): 225-245.

Booker J R. 2014. The magnetotelluric phase tensor: a critical review.SurveysinGeophysics, 35(1): 7-40.

Boschetto N B, Hohmann G W. 1991. Controlled-source audio frequency magnetotelluric responses of three-dimensional bodies.Geophysics, 56(2): 255-264.

Cai J H, Tang J T, Hua X R, et al. 2009. An analysis method for magnetotelluric data based on the Hilbert-Huang transform.ExplorationGeophysics, 40(2): 197-205.

Cai J H, Tang J T, Wang X C. 2011. Human noise elimination for magnetotelluric data based on empirical mode decomposition.JournalofCentralSouthUniversity(ScienceandTechnology) (in Chinese), 42(6): 1786-1790. Cai J H. 2013. Magnetotelluric response function estimation based on Hilbert-Huang transform.PureandAppliedGeophysics, 170(11): 1899-1911.

Cai J H. 2014. A combinatorial filtering method for magnetotelluric time-series based on Hilbert-Huang transform.ExplorationGeophysics, 45(2): 63-73.

Caldwell T G, Bibby H M, Brown C. 2004. The magnetotelluric phase tensor.GeophysicalJournalInternational, 158(2): 457-469.

Campanyà J, Ledo J, Queralt P, et al. 2014. A new methodology to estimate Magnetotelluric (MT) Tensor relationships: Estimation of Local transfer-functions by Combining Interstation Transfer-functions (ELICIT).GeophysicalJournalInternational, 198(1): 484-494.Emin Candansayar M, Tezkan B. 2008. Two-dimensional joint inversion of radiomagnetotelluric and direct current resistivity data.GeophysicalProspecting, 56(5): 737-749.

Cao C Q. 1978. The apparent resistivity for layered earth.ChineseJ.Geophys. (ActaGeophysicaSinica) (in Chinese), 21(3): 248-261.

Chant I J, Hastie L M. 1992. Time-frequency analysis of magnetotelluric data.GeophysicalJournalInternational, 111(2): 399-413.

Chave A D, Thomson D J, Ander M E. 1987. On the robust estimation of power spectra, coherences, and transfer functions.JournalofGeophysicalResearch:SolidEarth(1978—2012), 92(B1): 633-648. Chave A D, Thomson D J. 1989. Some Comments on magnetotelluric response function estimation.JournalofGeophysicalResearch:SolidEarth(1978—2012), 94(B10): 14215-14225.

Chave A D, Smith J T. 1994. On electric and magnetic galvanic distortion tensor decompositions.JournalofGeophysicalResearch, 99(B3): 4669-4682.

Chave A D, Thomson D J. 2003. A bounded influence regression estimator based on the statistics of the hat matrix.JournaloftheRoyalStatisticalSociety:SeriesC(AppliedStatistics), 52(3): 307-322.

Chave A D, Luther D S, Meinen C S. 2004. Correction of motional electric field measurements for galvanic distortion.JournalofAtmosphericandOceanicTechnology, 21(2): 317-330.

Chen H Y, Wei W B, Jing J E, et al. 2012. The generalized S-transform and its application in the processing of magnetotelluric sounding data.ProgressinGeophysics(in Chinese), 27(3): 988-996, doi: 10.6038/j.issn.1004-2903.

Chen J, Jegen-Kulcsar M, Moorkamp M. 2010. The empirical mode decomposition and hilbert instantaneous spectrum on MT data Processing. ∥20th International Electromagnetic Induction Workshop, Giza, Egypt.

Chen M S, Yan S. 2005. Analytical study on field zones, record rules, shadow and source overprint effects in CSAMT exploration.ChineseJ.Geophys. (in Chinese), 48(4): 951-958.

Chen W Y, Xue G Q. 2014. Effective skin depth of whole EM field due to a grounded wire source.ChineseJ.Geophys. (in Chinese), 57(7): 2314-2320, doi: 10.6038/cjg20140725.

Chen X B, Zhao G Z. 2009. Study on the transmitting mechanism of CSELF waves: response of the alternating current point source in the uniform space.ChineseJ.Geophys. (in Chinese), 52(8): 2158-2164, doi: 10.3969/j.issn.0001-5733.2009.08.026.

Chen X B, Cai J T, Wang L F, et al. 2014. Refined techniques for magnetotelluric data processing and two-dimensional inversion (IV): Statistical image method based on multi-site, multi frequency tensor decomposition.ChineseJ.Geophys. (in Chinese), 57(6): 1946-1957, doi: 10.6038/cjg20140625.

Cheng D F, Wang J, Li X P, et al. 2004. Development in the research of HSSMT instrument.ProgressinGeophysics(in Chinese), 19(4): 778-781, doi: 10.3969/j.issn.1004-2903.2004.04.012.

Cheng H, Li D Q. 2014. A new electromagnetic field division method for horizontal electric dipole.JournalofCentralSouthUniversity(ScienceandTechnology) (in Chinese), 45(7): 2250-2258.

Christopherson K R. 2012. Magnetotellurics (MT): Technique, Interpretation, and Application. http:∥www.searchanddiscovery.com/documents/geophysical/christopherson/index.htm.Coggon J H. 1971. Electromagnetic and electrical modeling by the finite element method.Geophysics, 36(1): 132-155.

Commer M, Newman G A. 2008. New advances in three-dimensional controlled-source electromagnetic inversion.GeophysicalJournalInternational, 172(2): 513-535. Cooley J W, Tukey J W. 1965. An algorithm for the machine calculation of complex Fourier series.MathematicsofComputation, 19(90): 297-301.

Cooley J W, Lewis P A, Welch P D. 1969. The fast Fourier transform and its applications.IEEETransactionsonEducation, 12(1): 27-34. Cui J L, Deng M, Jing J E, et al. 2013. Using independent component analysis to process magnetotelluric data.AppliedMechanicsandMaterials, 295-298: 2795-2798.

Das U C. 1995. Apparent resistivity curves in Controlled-source electromagnetic sounding directly reflecting true resistivities in a layered earth.Geophysics, 60(1): 53-60.

Di Q Y, Wang M Y, Wang R, et al. 2008. Study of the long dipole and large power electromagnetic field.ChineseJ.Geophys. (in Chinese), 51(6): 1917-1928.

Di Q Y, Fang G Y, Zhang Y M. 2013. Research of the Surface Electromagnetic Prospecting (SEP) system.ChineseJ.Geophys. (in Chinese), 56(11): 3629-3639, doi: 10.6038/cjg20131104.

Doherty J. 1988. EM modelling using surface integral equations.GeophysicalProspecting, 36(6): 644-668.

Egbert G D, Booker J R. 1986. Robust estimation of geomagnetic transfer functions.GeophysicalJournalInternational, 87(1): 173-194.

Egbert G D, Booker J R. 1989. Multivariate analysis of geomagnetic array data: 1. The response space.JournalofGeophysicalResearch:SolidEarth(1978—2012), 94(B10): 14227-14247. Egbert G D, Livelybrooks D W. 1996. Single Station magnetotelluric impedance estimation: coherence weighting and the regression M-estimate.Geophysics, 61(4): 964-970.

Egbert G D. 1997. Robust Multiple-station magnetotelluric data processing.GeophysicalJournalInternational, 130(2): 475-496.

Egbert G D. 2002. Processing and interpretation of electromagnetic induction array data.SurveysinGeophysics, 23(2-3): 207-249.

Escalas M, Queralt P, Ledo J, et al. 2013. Polarization analysis of magnetotelluric time series using a wavelet-based scheme: a method for detection and characterization of cultural noise sources.PhysicsoftheEarthandPlanetaryInteriors, 218: 31-50.

Everett M E. 2011. Theoretical developments in electromagnetic induction geophysics with selected applications in the near surface.SurveysinGeophysics, 33(1): 29-63.

Farquharson C G, Miensopust M P. 2011. Three-dimensional finite-element modelling of magnetotelluric data with a divergence correction.JournalofAppliedGeophysics, 75(4): 699-710.

Feng B, Wang J L, Zhou X W, et al. 2013. Application of full-region apparent resistivity of CSAMT Ex in exploration.CoalGeology&Exploration(in Chinese), 41(6): 78-82.

Fischer G, Weibel P. 1991. A new look at an old problem: Magnetotelluric modelling of 1-D structures.GeophysicalJournalInternational, 106(1): 161-167.

Fontes S L, Harinarayana T, Dawes G, et al. 1988. Processing of noisy magnetotelluric data using digital filters and additional data selection criteria.PhysicsoftheEarthandPlanetaryInteriors, 52(1): 30-40.

Franke A, Borner R U, Spitzer K. 2008. Is there a most efficient formulation of the three-dimensional magnetotelluric boundary value problem? ∥19th Workshop on Electromagnetic Induction in the Earth, Beijing, China.

Fu C M, Di Q Y, Xu C, et al. 2012. Electromagnetic fields for different type sources with effect of the ionosphere.ChineseJ.Geophys. (in Chinese), 55(12): 3958-3968, doi: 10.6038/j.issn.0001-5733.2012.12.008.

Fu C M, Di Q Y, An Z G. 2013. Application of the CSAMT method to groundwater exploration in a metropolitan environment.Geophysics, 78(5): B201-B209.

Gamble T, Goubau W M, Clarke J. 1979. Magnetotellurics with a remote magnetic reference.Geophysics, 44(1): 53-68.

Gao W. 1991. Line source effects on magnetotelluric responses.ChineseJ.Geophys. (in Chinese), 34(2): 210-215.

García X, Jones A G. 2005. A new methodology for the acquisition and processing of Audio-Magnetotelluric (AMT) data in the AMT dead band.Geophysics, 70(5): G119-G126.

Grayver A V, Bürg M. 2014. Robust and scalable 3D geo-electromagnetic modelling approach using the finite element method.GeophysicalJournalInternational, 198(1): 110-125.

Groom R W, Bailey R C. 1989. Decomposition of magnetotelluric impedance tensors in the presence of local Three-Dimensional galvanic distortion.JournalofGeophysicalResearch:SolidEarth(1978—2012), 94(B2): 1913-1925.

Groom R W, Bailey R C. 1991. Analytic investigations of the effects of Near-Surface Three-dimensional galvanic scatters on MT tensor decompositions.Geophysics, 56(4): 496-518.

Haber E, Ascher U M, Aruliah D A, et al. 2000. Fast simulation of 3D electromagnetic problems using potentials.JournalofComputationalPhysics, 163(1): 150-171.

Hattingh M. 1989. The use of Data-adaptive filtering for noise removal on magnetotelluric data.PhysicsoftheEarthandPlanetaryInteriors, 53(3-4): 239-254.

He J S. 1991. Controlled Source Audio-frequency Magnetotellurics (in Chinese). Changsha: Central South University Press.

He J S. 2010a. Closed addition in a three-element set and 2nsequence pseudo-random signal coding.JournalofCentralSouthUniversity(ScienceandTechnology) (in Chinese), 41(2): 632-627.

He J S. 2010b. Wide field electromagnetic sounding methods.JournalofCentralSouthUniversity(ScienceandTechnology) (in Chinese), 41(3): 1065-1072. He J S. 2010c. Wide Field Electromagnetic Method and Pseudo Random Signal Method (in Chinese). Beijing: Higher Education Press.

He L F, Wang X B, Wang C X. 1999. Improving the s/n ratio of MT data by wavelet analysis.JournalofChengduUniversityofTechnology(in Chinese), 26(3): 299-302.

Hohmann G W. 1975. Three-dimensional induced polarization and electromagnetic modeling.Geophysics, 40(2): 309-324.

Hou J S, Mallan R K, Torres-Verdín C. 2006. Finite-difference simulation of borehole EM measurements in 3D anisotropic media using coupled scalar-vector potentials.Geophysics, 71(5): G225-G233.

Hu W Y, Abubakar A, Habashy T M. 2009. Joint electromagnetic and seismic inversion using structural constraints.Geophysics, 74(6): R99-R109.

Hu Y F, He J S. 2015. Comparison of wide field electromagnetic method with CSAMT method in strong interferential mining area [Ph. D. thesis] (in Chinese). Changsha: Central South of University.

Huang H P, Piao H R. 1992. Full-wave apparent resistivity from vertical magnetic dipole frequency sounding on a layered earth.ChineseJ.Geophys. (in Chinese), 35(3): 389-395.

Huang L J, Lu G F, Liu R D, et al. 2004. The application of electromagnetic sounding method in deep geothermal investigation.Geophysical&GeochemicalExploration(in Chinese), 28(6): 493-495. Jiang L, Xu Y X. 2013. Multi-station superposition for magnetotelluric signal.StudiaGeophysicaEtGeodaetica, 57(2): 276-291.

Jing J E, Wei W B, Chen H Y, et al. 2012. Magnetotelluric sounding data processing based on generalized S transformation.ChineseJ.Geophys. (in Chinese), 55(12): 4015-4022, doi: 10.6038/j.issn.00015733. Jones A G, Chave A D, Egbert G D, et al. 1989. A comparison of techniques for magnetotelluric response function estimation.JournalofGeophysicalResearch:SolidEarth(1978—2012), 94(B10): 14201-14213.

Jones A G, Groom R W. 1993. Strike-angle determination from the magnetotelluric impedance tensor in the presence of noise and local distortion: Rotate at your peril!GeophysicalJournalInternational, 113(2): 524-534.

Kalscheuer T, Pedersen L B, Siripunvaraporn W. 2008. Radiomagnetotelluric two-dimensional forward and inverse modelling accounting for displacement currents.GeophysicalJournalInternational, 175(2): 486-514.

Kappler K N. 2012. A data variance technique for automated despiking of magnetotelluric data with a remote reference.GeophysicalProspecting, 60(1): 179-191.

Key K, Weiss C. 2006. Adaptive finite-element modeling using unstructured grids: the 2D magnetotelluric example.Geophysics, 71(6): G291-G299.La Terra E F, Menezes P T L. 2012. Audiomagnetotelluric 3D imaging of the Regis kimberlite pipe, Minas Gerais, Brazil.JournalofAppliedGeophysics, 77: 30-38.

Larsen J C, Mackie R L, Manzella A, et al. 1996. Robust smooth magnetotelluric transfer functions.GeophysicalJournalInternational, 124(3): 801-819. Lei D, Zhang G H, Huang G Y, et al. 2014. The application of tensor CSAMT method.ChineseJournalofEngineeringGeophysics(in Chinese), 11(3): 286-294.

Li Y G, Key K. 2007. 2D marine controlled-source electromagnetic modeling: Part 1—an adaptive finite-element algorithm.Geophysics, 72(2): WA51-WA62.

Liao Z L, Zhang Y J, Chen W B, et al. 2006. Available persist exploitation and utilization of geothermal resources.ChinaMiningMagazine(in Chinese), 15(10): 8-11.

Lin P R, Zheng C J, Shi F S, et al. 2006. The research of integrated electromagnetic method system.ActaGeologicaSinica(in Chinese), 80(10): 1539-1548.

Lin P R, Guo P, Shi F S, et al. 2010. A study of the techniques for large-depth and multi-functional electromagnetic survey.ActaGeoscienticaSinica(in Chinese), 31(2): 149-154.

Lin W. 2009. Transition region electromagnetic field characteristics of the CSAMT method.Geophysical&GeochemicalExploration(in Chinese), 33(2): 148-150. Liu E H, Lamontagne Y. 1998. Geophysical application of a new surface integral equation method for EM modeling.Geophysics, 63(2): 411-423.

Liu G M, Becker A. 1992. Evaluation of terrain effects in AEM surveys using the boundary element method.Geophysics, 57(2): 272-278.

Liu H, He L F, Wang X B, et al. 2004. Adaptability of wavelet analysis in MT noise-suppressed processing.OilGeophysicalProspecting(in Chinese), 39(3): 338-341.

Luo W B, Li Q C, Tang J T. 2012. Coded source electromagnetic sounding method.ChineseJ.Geophys. (in Chinese), 55(1): 341-349, doi: 10.6038/j.issn.0001-5733.2012.01.035.

Mackie R L, Smith J T, Madden T R. 1994. Three-dimensional electromagnetic modeling using finite difference equations: The magnetotelluric example.RadioScience, 29(4): 923-935.

Manoj C, Nagarajan N. 2003. The application of artificial neural networks to magnetotelluric time-series analysis.GeophysicalJournalInternational, 153(2): 409-423.

Mcneice G W, Jones A G. 2001. Multisite, multifrequency tensor decomposition of magnetotelluric data.Geophysics, 66(1): 158-173.

Meng Q K. 2013. Preliminary study of tensor CSAMT data acquisition and processing technology [Master′s thesis] (in Chinese). Beijing: Chinese Academy of Geological Sciences.

Mitsuhata Y, Uchida T. 2004. 3D magnetotelluric modeling using the T-Ω finite-element method.Geophysics, 69(1): 108-119.

Nam M J, Kim H J, Song Y, et al. 2007. 3D magnetotelluric modelling including surface topography.GeophysicalProspecting, 55(2): 277-287. Nédélec J. 1986. A new family of mixed finite elements in R3.NumerischeMathematik, 50(1): 57-81.

Neukirch M, Garcia X. 2014. Nonstationary magnetotelluric data processing with instantaneous parameter.JournalofGeophysicalResearch:SolidEarth, 119(3): 1634-1654.Newman G A, Alumbaugh D L. 1997. Three-dimensional massively parallel electromagnetic inversion—I. theory.GeophysicalJournalInternational, 128(2): 345-354.

Newman G A, Alumbaugh D L. 1999. 3-D electromagnetic modeling and inversion on massively parallel computers. ∥ Oristaglio M N, Spies B R eds. Three-Dimensional Electromagnetics. Society of exploration geophysicists, Geophysical Developments No. 7, Tulsa OK, 299-321. Newman G A, Alumbaugh D. 2002. Three-dimensional induction logging problems, part 2: a finite-difference solution.Geophysics, 67(2): 484-491. Newman G A, Recher S, Tezkan B, et al. 2003. 3D inversion of a scalar radio magnetotelluric field data set.Geophysics, 68(3): 791-802.

Newman G A, Commer M, Carazzone J J. 2010. Imaging CSEM data in the presence of electrical anisotropy.Geophysics, 75(2): F51-F61.

Oettinger G, Haak V, Larsen J C. 2001. Noise reduction in magnetotelluric Time-series with a new signal-noise separation method and its application to a field experiment in the Saxonian granulite massif.GeophysicalJournalInternational, 146(3): 659-669.

Parker R L. 1980. The inverse problem of electromagnetic induction: existence and construction of solutions based on incomplete data.JournalofGeophysicalResearch:SolidEarth(1978—2012), 85(B8): 4421-4428.

Parker R L, Whaler K A. 1981. Numerical methods for establishing solutions to the inverse problem of electromagnetic induction.JournalofGeophysicalResearch:SolidEarth(1978—2012), 86(B10): 9574-9584.

Parker R L, Booker J R. 1996. Optimal One-dimensional inversion and bounding of magnetotelluric apparent resistivity and phase measurements.PhysicsoftheEarthandPlanetaryInteriors, 98(3-4): 269-282.

Parry J R, Ward S H. 1971. Electromagnetic scattering from cylinders of arbitrary cross-section in a conductive half-space.Geophysics, 36(1): 67-100.

Penz S, Chauris H, Donno D, et al. 2013. Resistivity modelling with topography.GeophysicalJournalInternational, 194(3): 1486-1497.

Prácser E, Szarka L. 1999. A correction to Bahr′s “Phase Deviation” method for tensor decomposition.Earth,PlanetsandSpace, 51(10): 1019-1022.

Puzyrev V J, Koldan J, de la Puente J, et al. 2013. A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling.GeophysicalJournalInternational, 193(2): 678-693.Raiche A P. 1974. An integral equation approach to three-dimensional modelling.GeophysicalJournaloftheRoyalAstronomicalSociety, 36(2): 363-376.

Ren. 2012. New Developments in Numerical Modeling of Broadband Geo-electromagnetic Fields. Zurich: ETH Zurich Press.

Ren Z Y, Tang J T. 2010. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method.Geophysics, 75(1): H7-H17

Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2012. Boundary element solutions for broadband 3D geo-electromagnetic problems accelerated by multi-level fast multipole method.GeophysicalJournalInternational, 192(2): 473-499.

Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. A goal-oriented adaptive finite-element approach for plane wave 3D electromagnetic modelling.GeophysicalJournalInternational, doi: 10.1093/gji/ggt154. Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2014. A finite-element based domain-decomposition approach for plane wave 3D electromagnetic modeling.Geophysics, 79(6): E255-E268.

Ritter O, Junge A, Dawes G. 1998. New equipment and processing for magnetotelluric remote reference observations.GeophysicalJournalInternational, 132(3): 535-548.

Schenk O, Gärtner K. 2004. Solving unsymmetric sparse systems of linear equations with PARDISO.FutureGenerationComputerSystems, 20(3): 475-487.

Schwarzbach C, Börner R U, Spitzer K. 2011. Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics—a marine CSEM example.GeophysicalJournalInternational, 187(1): 63-74. Sheard S N, Ritchie T J, Christopherson K R, et al. 2005. Mining, environmental, petroleum, and engineering industry applications of electromagnetic techniques in geophysics.SurveysinGeophysics, 26(5): 653-669.Sims W E, Bostick Jr F X, Smith H W. 1971. The estimation of magnetotelluric impedance tensor elements from measured data.Geophysics, 36(5): 938-942.

Siripunvaraporn W, Egbert G, Lenbury Y. 2002. Numerical accuracy of magnetotelluric modeling: a comparison of finite difference approximations.Earth,PlanetsandSpace, 54(6): 721-725.

Siripunvaraporn W, Sarakorn W. 2011. An efficient data space conjugate gradient Occam′s method for three-dimensional magnetotelluric inversion.GeophysicalJournalInternational, 186(2): 567-579.

Smirnov M Y, Egbert G D. 2012. Robust principal component analysis of electromagnetic arrays with missing data.GeophysicalJournalInternational, 190(3): 1423-1438. Smirnov M Y. 2003. Magnetotelluric data processing with a robust statistical procedure having a high breakdown point.GeophysicalJournalInternational, 152(1): 1-7. Smith J T. 1996. Conservative modeling of 3-D electromagnetic fields, Part II: bi-conjugate gradient solution and an accelerator.Geophysics, 61(5): 1319-1324.Smith R. 2014. Electromagnetic induction methods in mining geophysics from 2008 to 2012.SurveysinGeophysics, 35(1): 123-156.

Sokolova E Y, Varentsov M I, Group E P W. 2005. The RRMC Technique fights highly coherent EM noise. ∥ Dtsch. Geophys. Ges. Potsdam, Germany, 124-136.

Song S G, Tang J T, He J S. 1995. Wavelets analysis and the recognition, separation and removal of the static shift in electromagnetic soundings.ChineseJ.Geophys. (in Chinese), 38(1): 120-128.

Spratt J E, Jones A G, Nelson K D, et al. 2005. Crustal structure of the India-Asia collision zone, Southern Tibet, from INDEPTH MT investigations.PhysicsoftheEarthandPlanetaryInteriors, 150(1-3): 227-237. Sternberg B K, Washburne J C, Pellerin L. 1988. Correction for the static shift in magnetotellurics using transient electromagnetic soundings.Geophysics, 53(11): 1459-1468.

Streich R. 2009. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data: direct solution and optimization for high accuracy.Geophysics, 74(5): F95-F105.

Sutarno D. 2008. Development of robust magnetotelluric impedance estimation: a review.IndonesianJournalofPhysics, 16(3): 79-89.

Swift Jr C M. 1967. A magnetotelluric investigation an electrical conductivity anomaly in the southwestern United States [Ph. D. thesis]. Massachusetts: Massachusetts Institute of Technology.Tang J T, He J S. 1993. Effective resistivity defined by the electromagnetic fields induced by horizontal electric dipole.JournalofCentralSouthInstituteofMiningandMetallurgy(in Chinese), 24(2): 137-142.

Tang J T, He J S. 1994a. A new method to define the full-zone resistivity in horizontal electric dipole frequency soundings on a layered earth.ChineseJ.Geophys. (in Chinese), 37(4): 543-552.

Tang J T, He J S. 1994b. Impedance real part equivalent resistivity in frequency electromagnetic sounding of horizontal electric double source on horizontal multilayer media.Geophysical&GeochemicalExploration(in Chinese), 18(2): 92-96.

Tang J T, He J S. 2005. Methods and Applications of CSAMT (in Chinese). Changsha: Central South University Press.

Tang J T, Hua X R, Cao Z M, et al. 2008. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data.ChineseJ.Geophys. (in Chinese), 51(2): 603-610.

Tang J T, Cai J H, Ren Z Y, et al. 2009. Hilbert-Huang transform and time frequency analysis of magnetotelluric signal.JournalofCentralSouthUniversity(ScienceandTechnology) (in Chinese), 40(5): 1399-1405

Tang J T, Zhou C, Zhang L C. 2011. A new apparent resistivity of CSAMT defined by electric fieldy-direction.JournalofJilinUniversity(EarthScienceEdition) (in Chinese), 41(2): 552-558.

Tang J T, Li J, Xiao X, et al. 2012a. Mathematical morphology filtering and noise suppression of magnetotelluric sounding data.ChineseJ.Geophys. (in Chinese), 55(5): 1784-1793, doi: 10.6038/j.issn.0001-5733.2012.05.036.

Tang J T, Xu Z M, Xiao X, et al. 2012b. Effect rules of strong noise on magnetotelluric (MT) sounding in the Luzong ore cluster area.ChineseJ.Geophys. (in Chinese), 55(12): 4147-4159, 10.6038/j.issn.0001-5733.2012.12.027.

Tang J T, Ge W N. 2012. Shadow and source overprint effects in 3D CSAMT.ComputingTechniquesforGeophysical&GeochemicalExploration(in Chinese), 34(1): 19-26.

Tang J T, Zhou C, Wang X Y, et al. 2013. Deep electrical structure and geological significance of Tongling ore district.Tectonophysics, 606: 78-96.

Tang J T, Zhang C, Xiao X, et al. 2013a. Comparison of methods for magnetotelluric impedance estimation.TheChineseJournalofNonferrousMetals(in Chinese), 23(9): 2351-2358.

Tang J T, Zhou C, Xiao X. 2013b. Selection of minimum transmit-receive distance of CSAMT on complicated media.TheChineseJournalofNonferrousMetals(in Chinese), 23(6): 1681-1693.

Tezkan B, Hördt A, Gobashy M. 2000. Two-dimensional radiomagnetotelluric investigation of industrial and domestic waste sites in Germany.JournalofAppliedGeophysics, 44(2-3): 237-256.

Tezkan B, Georgescu P, Fauzi U. 2005. A radiomagnetotelluric survey on an oil-contaminated area near the Brazi Refinery, Romania.GeophysicalProspecting, 53(3): 311-323.

Tezkan B, Goldman M, Greinwald S, et al. 1996. A joint application of radiomagnetotellurics and transient electromagnetics to the investigation of a waste deposit in Cologne (Germany).JournalofAppliedGeophysics, 34(3): 199-212. Torres-Verdín C, Bostick Jr F X. 1992. Principles of spatial surface electric field filtering in magnetotellurics: Electromagnetic Array Profiling (EMAP).Geophysics, 57(4): 603-622. Trad D O, Travassos J M. 2000. Wavelet filtering of magnetotelluric data.Geophysics, 65(2): 482-491. Turberg P, Müller I, Flury F. 1994. Hydrogeological investigation of porous environments by radio magnetotelluric-resistivity (RMT-R 12-240 kHz).JournalofAppliedGeophysics, 31(1-4): 133-143.

Tzanis A, Beamish D. 1989. A high-resolution spectral study of audiomagnetotelluric data and noise interactions.GeophysicalJournalInternational, 97(3): 557-572.

Vallée M A, Smith R S, Keating P. 2011. Metalliferous mining geophysics-State of the art after a decade in the new millennium.Geophysics, 76(4): W31-W50.

Varentsov I M, Sokolova E Y, Martanus E R, et al. 2003. System of electromagnetic field transfer operators for the BEAR array of simultaneous soundings: methods and results.Izvestiya-PhysicsoftheSolidEarth, 39(2): 118-148.

Varentsov I M. 2006. Arrays of simultaneous electromagnetic soundings: design, data processing and analysis. ∥ Electromagnetic Sounding of the Earth′s Interior, Vol. 40. Methods in Geochemistry and Geophysics. Amsterdam: Elsevier, 259-273. Wang H, Wei W B, Jin S, et al. 2014. Removal of magnetotelluric noise based on synchronous time series relationship.ChineseJ.Geophys. (in Chinese), 57(2): 531-545, doi: 10.6038/cjg20140218.

Wang R, Wang M Y, Lu Y L. 2004. CSAMT observation system study in high mountain and steep gorge area.ProgressinGeophysics(in Chinese), 19(1): 125-130, doi: 10.3969/j.issn.1004-2903.2004.01.018.

Wang R, Di Q Y, Wang M Y, et al. 2009. Research on the effect of 3D body between transmitter and receivers on CSAMT response using Integral Equation method.ChineseJ.Geophys. (in Chinese), 52(6): 1573-1582, doi: 10.3969/j.issn.0001-5733.2009.06.019.

Wang S M, Wang J Y. 2004. Application of higher-order statistics in magnetotelluric data processing.ChineseJ.Geophys. (in Chinese), 47(5): 928-934.

Wang X X, Di Q Y, Xu C. 2014. Characteristics of multiple sources and tensor measurement in CSAMT.ChineseJ.Geophys. (in Chinese), 57(2): 651-661, doi: 10.6038/cjg20140228.

Weaver J T, Agarwal A K, Lilley F E M. 2006. The relationship between the magnetotelluric tensor invariants and the phase tensor of Caldwell, Bibby, and Brown.ExplorationGeophysics, 37(3): 261-267.Weckmann U, Magunia A, Ritter O. 2005. Effective noise separation for magnetotelluric single site data processing using a frequency domain selection scheme.GeophysicalJournalInternational, 161(3): 635-652.

Weidelt P. 1972. The inverse problem of geomagnetic induction.J.Geophys., 38: 257-289.

Weidelt P. 1975. Electromagnetic induction in three-dimensional structures.J.Geophys., 41: 85-109.

Weiss C J, Schultz A. 2011. An evaluation of parallelization strategies for low-frequency electromagnetic induction simulators using staggered grid discretizations. ∥ American Geophysical Union Fall Meeting Conference Proceedings, Informatics Session, San Francisco.

Xia S B, Min G, Qiu L, et al. 2012. A study of MT method on the prospecting for deep ore deposits.ChineseJournalofEngineeringGeophysics(in Chinese), 9(5): 531-536.

Xu S Z, Ruan B Y, Zhou H, et al. 1997. Numerical modeling of 3-D terrain effect on MT field.ScienceinChinaSeriesD:EarthSciences, 40(3): 269-275.

Xu Y X, Wang J Y. 2000. Power spectrum estimation for magnetotelluric signal based on continuous wavelet transform.ChineseJ.Geophys. (in Chinese), 43(5): 677-683.

Xu Z F, Wu X P. 2010. Electromagnetic fields excited by the horizontal electrical dipole on the surface of the ionosphere-homogeneous earth model.ChineseJ.Geophys. (in Chinese), 53(10): 2497-2506, 10.3969/j.issn.0001-5733.2010.10.023.

Yan J B, Liu G Z. 2007. Like-impulse electromagnetic noise processing based wavelet transform.CoalGeology&Exploration(in Chinese), 35(5): 61-65.

Yan S, Chen M S. 1996. Static offset and correction in frequency domain electromagnetic sounding.OilGeophysicalProspecting(in Chinese), 31(2): 238-247. Yan S, Chen M S. 2004. Shadow and source overprint effects in CSAMT sounding.OilGeophysicalProspecting(in Chinese), 39(S1): 8-10.

Yang S, Bao G S, Zhang S Y. 2001. The correction to aberrant appearance resistivity curve by using impedance phase data in magnetotelluric method.Geology&Prospecting(in Chinese), 37(6): 42-45.Ye Y X, Deng J Z, Li M, et al. 2011. Application status and vistas of electromagnetic methods to deep ore prospecting.ProgressinGeophysics(in Chinese), 26(1): 327-334, doi: 10.3969/j.issn.10042903.2011.01.039.

Yin C C, Piao H R. 1991. A study of the definition of apparent resistivity in electromagnetic sounding.Geophysical&GeochemicalExploration(in Chinese), 15(4): 290-299.

Yue R Y, Xu Y X. 2004. Study on electric azimuth anisotropy of controlled source in frequency domain and Near-field effects.OilGeophysicalProspecting(in Chinese), 39(3): 342-347.

Zhan S Q, Qian M P, Feng J J. 2011. The CSAMT near-field correction method for electric field apprarent resistivity forward iterative fitting.Geophysical&GeochemicalExploration(in Chinese), 35(5): 663-665.

Zhang Y, Paulson K V. 1997. Enhancement of signal-to-noise ratio in natural-source transient magnetotelluric data with wavelet transform.PureandAppliedGeophysics, 149(2): 405-419.

Zhao G Z, Wang L F, Tang J, et al. 2010. New experiments of CSELF electromagnetic method for earthquake monitoring.ChineseJ.Geophys. (in Chinese), 53(3): 479-486, doi: 10.3969/j.issn.0001-5733.2010.03.002.

Zhdanov M S, Lee S K, Yoshioka K. 2006. Integral equation method for 3D modeling of electromagnetic fields in complex structures with inhomogeneous background conductivity.Geophysics, 71(6): G333-G345.

Zhdanov M S. 2010. Electromagnetic geophysics: Notes from the past and the road ahead.Geophysics, 75(5): 75A49-75A66.

Zhen Q H, Di Q Y, Liu H B. 2013. Key technology study on CSAMT transmitter with excitation control.ChineseJ.Geophys. (in Chinese), 56(11): 3751-3760, doi: 10.6038/cjg20131116.

Zhou H F, Liu C, Shi K F. 2003. A review of study on geothermal resources exploration.ProgressinGeophysics(in Chinese), 18(4): 656-661, doi: 10.3969/j.issn.1004-2903.2003.04.014.

Zhuo X J, Lu J X. 2010. Application and prospect of WFEM to resource exploration and earthquake predication.ShipScienceandTechnology(in Chinese), 32(6): 3-7.

Zhuo X J, Lu J X, Zhao G Z, et al. 2011. The extremely low frequency engineering project using WFEM for underground exploration.EngineeringScience(in Chinese), 13(9): 42-50.

附中文参考文献

蔡剑华, 汤井田, 王先春. 2011. 基于经验模态分解的大地电磁资料人文噪声处理. 中南大学学报(自然科学版), 42(6): 1786-1790.

曹昌祺. 1978. 水平分层大地的交流视电阻率. 地球物理学报, 21(3): 248-261.

陈海燕, 魏文博, 景建恩等. 2012. 广义 S 变换及其在大地电磁测深数据处理中的应用. 地球物理学进展, 27(3): 988-996, doi: 10.6038/j.issn.1004-2903.

陈明生, 闫述. 2005. CSAMT勘探中场区、记录规则、阴影及场源复印效应的解析研究. 地球物理学报, 48(4): 951-958.

陈卫营, 薛国强. 2014. 接地导线源电磁场全域有效趋肤深度. 地球物理学报, 57(7): 2314-2320, doi: 10.6038/cjg20140725.

陈小斌, 赵国泽. 2009. 关于人工源极低频电磁波发射源的讨论—均匀空间交流点电流源的解. 地球物理学报, 52(8): 2158-2164, doi: 10.3969/j.issn.0001-5733.2009.08.026.

陈小斌, 蔡军涛, 王立凤等. 2014. 大地电磁资料精细处理和二维反演解释技术研究(四)——阻抗张量分解的多测点-多频点统计成像分析. 地球物理学报, 57(6): 1946-1957, doi: 10.6038/cjg20140625.

程德福, 王君, 李秀平等. 2004. 混场源电磁法仪器研制进展. 地球物理学进展, 19(4): 778-781, doi: 10.3969/j.issn.1004-2903.2004.04.012.

程辉, 李帝铨. 2014. 一种新的水平电偶极子电磁波场区划分方法. 中南大学学报 (自然科学版), 45(7): 2250-2258.

底青云, 方广有, 张一鸣. 2013. 地面电磁探测系统(SEP)研究. 地球物理学报, 56(11): 3629-3639, doi: 10.6038/cjg20131104.

底青云, 王妙月, 王若等. 2008. 长偶极大功率可控源电磁波响应特征研究. 地球物理学报, 51(6): 1917-1928.

冯兵, 王珺璐, 周祥文等. 2013. CSAMT探测中电场Ex全区视电阻率定义及应用. 煤田地质与勘探, 41(6): 78-82.

付长民, 底青云, 许诚等. 2012. 电离层影响下不同类型源激发的电磁场特征. 地球物理学报, 55(12): 3958-3968, doi: 10.6038/j.issn.0001-5733.2012.12.008.

高文. 1991. 大地电磁感应的场源效应. 地球物理学报, 34(2): 210-215. 何继善. 1991. 可控源音频大地电磁法. 长沙: 中南工业大学出版社. 何继善. 2010a. 三元素集合中的自封闭加法与 2n系列伪随机信号编码. 中南大学学报 (自然科学版), 41(2): 632-627.

何继善. 2010b. 广域电磁测深法研究. 中南大学学报(自然科学版), 41(3): 1065-1072.

何继善. 2010c. 广域电磁法和伪随机信号电法. 北京: 高等教育出版社.

何兰芳, 王绪本, 王成祥. 1999. 应用小波分析提高MT资料信噪比. 成都理工学院学报, 26(3): 299-302.

胡艳芳, 何继善. 2015. 强干扰矿区广域电磁法与CSAMT法对比[硕士论文]. 长沙:中南大学.

黄皓平, 朴化荣. 1992. 水平多层大地上垂直磁偶极频率测深的全波视电阻率. 地球物理学报, 35(3): 389-395.

黄力军, 陆桂福, 刘瑞德等. 2004. 电磁测深方法在深部地热资源调查中的应用. 物探与化探, 28(6): 493-495.

景建恩, 魏文博, 陈海燕等. 2012. 基于广义S变换的大地电磁测深数据处理. 地球物理学报, 55(12): 4015-4022, doi: 10.6038/j.issn.00015733.

雷达, 张国鸿, 黄高元等. 2014. 张量可控源音频大地电磁法的应用实例. 工程地球物理学报, 11(3): 286-294.

李帝铨, 底青云, 王妙月. 2011. “地-电离层”模式有源电磁场一维正演. 地球物理学报, 54(9): 2375-2388, doi: 10.3969/j.issn.0001-5733.2011.09.021.

廖忠礼, 张予杰, 陈文彬等. 2006. 地热资源的特点与可持续开发利用. 中国矿业, 15(10): 8-11.

林品荣, 郭鹏, 石福升等. 2010. 大深度多功能电磁探测技术研究. 地球学报, 31(2): 149-154.

林品荣, 郑采君, 石福升等. 2007. 电磁法综合探测系统研究. 地质学报, 80(10): 1539-1548.

林威. 2009. CSAMT法过渡区电磁场的特征. 物探与化探, 33(2): 148-150.

刘宏, 何兰芳, 王绪本等. 2004. 小波分析在 MT 去噪处理中的适定性. 石油地球物理勘探, 39(3): 338-341.

罗维斌, 李庆春, 汤井田. 2012. 编码电磁测深. 地球物理学报, 55(1): 341-349, doi: 10.6038/j.issn.0001-5733.2012.01.035.

孟庆奎. 2013. 张量CSAMT数据采集与处理技术初步研究[硕士论文]. 北京: 中国地质科学院.

宋守根, 汤井田, 何继善. 1995. 小波分析与电磁测深中静态效应的识别, 分离及压制. 地球物理学报, 38(1): 120-128.

汤井田, 何继善. 1993. 水平电偶极子源的场分量等效电阻率. 中南矿冶学院学报, 24(2): 137-142.

汤井田, 何继善. 1994a. 水平电偶源频率测深中全区视电阻率定义的新方法. 地球物理学报, 37(4): 543-552.

汤井田, 何继善. 1994b. 水平多层介质上水平电偶源频率电磁测深的阻抗实部等效电阻率. 物探与化探, 18(2): 92-96.

汤井田, 何继善. 2005. 可控源音频大地电磁法及其应用. 长沙: 中南大学出版社.

汤井田, 化希瑞, 曹哲民等. 2008. Hilbert-Huang 变换与大地电磁噪声压制. 地球物理学报, 51(2): 603-610.

汤井田, 蔡剑华, 任政勇等. 2009. Hilbert-Huang 变换与大地电磁信号的时频分析. 中南大学学报(自然科学版), 40(5): 1399-1405.

汤井田, 周聪, 张林成. 2011. CSAMT电场y方向视电阻率的定义及研究. 吉林大学学报(地球科学版), 41(2): 552-558.

汤井田, 李晋, 肖晓等. 2012a. 数学形态滤波与大地电磁噪声压制. 地球物理学报, 55(5): 1784-1793, doi: 10.6038/j.issn.0001-5733.2012.05.036.

汤井田, 徐志敏, 肖晓等. 2012b. 庐枞矿集区大地电磁测深强噪声的影响规律. 地球物理学报, 55(12): 4147-4159, 10.6038/j.issn.0001-5733.2012.12.027.

汤井田, 葛伟男. 2012. 三维 CSAMT 中的阴影和场源附加效应. 物探化探计算技术, 34(1): 19-26.

汤井田, 张弛, 肖晓等. 2013a. 大地电磁阻抗估计方法对比. 中国有色金属学报, 23(9): 2351-2358.

汤井田, 周聪, 肖晓. 2013b. 复杂介质条件下CSAMT最小发收距的选择. 中国有色金属学报, 23(6): 1681-1693.

王辉, 魏文博, 金胜等. 2014. 基于同步大地电磁时间序列依赖关系的噪声处理. 地球物理学报, 57(2): 531-545, doi: 10.6038/cjg20140218.

王若, 王妙月, 卢元林. 2004. 高山峡谷区CSAMT观测系统研究.地球物理学进展, 19(1): 125-130, doi: 10.3969/j.issn.1004-2903.2004.01.018.

王若, 底青云, 王妙月等. 2009. 用积分方程法研究源与勘探区之间的三维体对CSAMT观测曲线的影响. 地球物理学报, 52(6): 1573-1582, doi: 10.3969/j.issn.0001-5733.2009.06.019. 王书明, 王家映. 2004. 高阶统计量在大地电磁测深数据处理中的应用研究. 地球物理学报, 47(5): 928-934.

王显祥, 底青云, 许诚. 2014. CSAMT的多偶极子源特征与张量测量. 地球物理学报, 57(2): 651-661, doi: 10.6038/cjg20140228. 夏时斌, 闵刚, 邱林等. 2012. 大地电磁 (MT) 法在深部矿产勘探中的分辨率探讨. 工程地球物理学报, 9(5): 531-536.

徐义贤, 王家映. 2000. 基于连续小波变换的大地电磁信号谱估计方法. 地球物理学报, 43(5): 677-683.

徐志锋, 吴小平. 2010. 电离层-均匀地球模型中地表水平电偶极子激发的电磁场. 地球物理学报, 53(10): 2497-2506, 10.3969/j.issn.0001-5733.2010.10.02.

严家斌, 刘贵忠. 2007. 基于小波变换的脉冲类电磁噪声处理. 煤田地质与勘探, 35(5): 61-65.

阎述, 陈明生. 1996. 频率域电磁测深的静态偏移及校正方法. 石油地球物理勘探, 31(2): 238-247.

闫述, 陈明生. 2004. CSAMT测深中的阴影和场源复印效应问题. 石油地球物理勘探, 39(增刊): 8-10.

杨生, 鲍光淑, 张少云. 2001. MT 法中利用阻抗相位资料对畸变视电阻率曲线的校正. 地质与勘探, 37(6): 42-45.

叶益信, 邓居智, 李曼等. 2011. 电磁法在深部找矿中的应用现状及展望. 地球物理学进展, 26(1): 327-334, doi: 10.3969/j.issn.10042903.2011.01.039. 殷长春, 朴化荣. 1991. 电磁测深法视电阻率定义问题的研究. 物探与化探, 15(4): 290-299.

岳瑞永, 徐义贤. 2004. 可控源频率域电方位各向异性与近场效应研究. 石油地球物理勘探, 39(3): 342-347.

詹少全, 钱美平, 冯戋戋. 2011. CSAMT 全区视电阻率电场正演迭代拟合近场校正方法. 物探与化探, 35(5): 663-665.

赵国泽, 王立凤, 汤吉等. 2010. 地震监测人工源极低频电磁技术(CSELF)新试验. 地球物理学报, 53(3): 479-486, doi: 10.3969/j.issn.0001-5733.2010.03.002.

真齐辉, 底青云, 刘汉北. 2013. 励磁控制的CSAMT发送机若干技术研究. 地球物理学报, 56(11): 3751-3760, doi: 10.6038/cjg20131116.

周厚芳, 刘闯, 石昆法. 2004. 地热资源探测方法研究进展. 地球物理学进展, 18(4): 656-661, doi: 10.3969/j.issn.1004-2903.2003.04.014.

卓贤军, 陆建勋. 2010. “极低频探地工程”在资源探测和地震预测中的应用与展望. 舰船科学技术, 32(6): 3-7.

卓贤军, 陆建勋, 赵国泽等. 2011. 极低频探地(WEM)工程. 中国工程科学, 13(9): 42-50.

(本文编辑 何燕)

Frequency-domain electromagnetic methods for exploration of the shallow subsurface: A review

TANG Jing-Tian1,2, REN Zheng-Yong1,2, ZHOU Cong1,2, ZHANG Lin-Cheng1,2, YUAN Yuan1,2, XIAO Xiao1,2

1KeyLaboratoryofMetallogenicPredictionofNon-FerrousMetalsandGeologicalEnvironmentMonitor，MinistryofEducation，CentralSouthUniversity,Changsha410083，China2InstituteofAppliedGeophysics,SchoolofGeosciencesandInfo-Physics，CentralSouthUniversity,Changsha410083，China

Four electromagnetic (EM) methods are widely used in exploration of the shallow subsurface (above depth 2000 meters), which are the audio-frequency magnetotellurics (AMT), radio-magnetotellurics (RMT), controlled source audio-frequency magnetotellurics (CSAMT) and the wide-field electromagnetic methods (WFEM). The purpose of this review is to present the advances of these technologies from five aspects, i.e. data collection, data processing algorithms, forward modeling, inversion algorithms and case studies. We also point out their current difficulties and suggest the potential development trends.To address the issues above, we have made a detailed investigation to the recent literature and chosen the most significant papers published.(1) Data acquisition and instrument. Along with the growing power of EM data collection instruments, the tensor measurement has been commonly adopted. In order to obtain more reliable data, instrument array or multi-instruments have been widely used in the field. By large funds for developing instruments, the quality of domestic instruments is gradually approaching that of the foreign equipment. (2) Data processing algorithms. The time series of AMT data usually contains different types of noise, such as artificial square waves and industry noise around target zones. Therefore, the signal-to-noise ratio of AMT data is usually low. In order to obtain useful signals, we can utilize the robust digital morphological filtering technology. In transforming the time domain signal into the frequency domain, the Hilbert Huang transform is a suitable choice. Recently, the main reliable approach to estimate the tensor impedance is simultaneously using multi-channel multi-frequency data. As for the CSAMT and RMT methods, the state of art in the data acquisition is to identify near field and far field zones. A new idea is the wide-band electromagnetic acquisition technique, which presents a unified way to compute the apparent resistivity in both near field and far field zones. Compared to the AMT, RMT and CSAMT methods, the WFEM method can work better in the near field zone. (3) Forward modeling and inversion. In order to compute the EM responses for complicated AMT/RMT/CSAMT problems, the finite element method has become the indispensable tool. The edge-based finite-element methods have replaced the nodal-based finite-element methods. To have a capability of dealing with complicated topography, the unstructured grids instead of traditional structured grids have become more important. The high efficiency of direct solvers such as MUMPS and Pardiso have played an important role in solving multi-source EM problems. As for the inversion, to simulate 3D cases, two inversion algorithms, which are the nonlinear conjugate gradient method and Gauss-Newton algorithm, have been applied to successfully performing 3D inversion of AMT/RMT/CSAMT data. To further improve the inversion quality, the joint inversion scheme becomes more popular. (4) Applications. The above AMT/RMT/CSAMT methods are widely used in mineral resources exploration, geothermal resources or groundwater surveys, and environmental and engineering geophysics. In inverting the AMT/RMT/CSAMT data, we should analyze the possible dimensionality of the subsurface structure. When they show a 2D structure, the results by 2D inversion are reliable. However, for 3D cases, inversion results and geological interpretations must be based on 3D inversion algorithms.

Shallow subsurface exploration; Frequency-domain electromagnetic methods; AMT; RMT; CSAMT; WFEM

国家自然科学基金(41104071,41574120,41174105)，国家高技术研究发展计划(863)项目(2014AA06A602),国家重点基础研究发展规划(青年973)项目(2015CB060201)资助.

汤井田，男，1965年生，教授，博士生导师，主要研究方向:电磁法正反演研究及相关数据处理.E-mail:jitang@mail.csu.edu.cn

10.6038/cjg20150807.

10.6038/cjg20150807

P631

2014-12-22，2015-06-25收修定稿

汤井田， 任政勇，周聪等. 2015. 浅部频率域电磁勘探方法综述.地球物理学报，58(8):2681-2705,

Tang J T, Ren Z Y, Zhou C,et al. 2015. Frequency-domain electromagnetic methods for exploration of the shallow subsurface: A review.ChineseJ.Geophys. (in Chinese),58(8):2681-2705,doi:10.6038/cjg20150807.