角度域剩余深度对剩余速度的敏感性分析

徐嘉亮, 常旭, 王一博

中国科学院地质与地球物理研究所， 北京 100029



角度域剩余深度对剩余速度的敏感性分析

徐嘉亮, 常旭, 王一博

中国科学院地质与地球物理研究所， 北京 100029

本文针对地震勘探深度域偏移速度建模研究,利用角度域共成像点道集(ADCIGS)建立了以剩余速度为自变量，剩余深度为目标函数的关系式，及目标函数的梯度公式.利用导出的两个公式分别对剩余深度与剩余速度的关系进行了定量分析.通过理论分析和模型试算证明初始速度模型的误差具有方向敏感性，即正误差较负误差对速度建模迭代收敛更敏感.利用此结论进行深度域速度建模既可以提高计算效率也可以提高建模精度.

深度域偏移速度分析； 角度域共成像点道集； 剩余深度； 剩余速度

1 引言

随着石油勘探程度的不断提高，地球物理研究面临越发复杂的地质构造.一般来说，深层的复杂地质构造具有岩性横向变化较大，介质速度横向变化剧烈、以及地层倾角较大的特点，造成地震勘探的常规处理流程难以获得清晰的地下构造信息.因此，针对复杂构造的高精度叠前深度偏移成像的研究就显得尤为重要.叠前深度偏移只有在深度域速度模型准确度较高的情况下才能够正确成像.因此，深度域的速度建模成为叠前深度偏移的重要基础.深度域速度建模方法中初始速度的求取以及速度模型的迭代修正是获得准确的深度域速度模型的关键，开展这些关键方法技术的研究对于提高叠前深度偏移的精度具有重要的理论和实际意义(Mackay et al.,1993).

目前经常使用的两种基于叠前深度偏移的速度更新方法为深度聚焦分析方法DFA(Depth focusing analysis)和剩余曲率分析方法RCA(Residual curvature analysis).其中最常应用的是剩余曲率的分析方法.1989年，Al-Yahya(1989)基于共成像点道集拉平准则建立了剩余曲率的分析方法.这种方法最先把速度分析和偏移成像联系在了一起.此后，Lee和Zhang(1992)给出了带倾角校正的剩余校正公式，将水平层状地层推广到小倾角地层.近些年，针对不同类型的共成像点道集，发展了不同道集的RCA速度分析方法.其中角度域共成像点道集的速度分析方法发展较快.Prucha等(1999)利用倾斜叠加算法在双平方根DSR(Double square root)方程偏移中分解了与角度相关的偏移距射线参数域道集. Rickett和Sava(2002)通过倾斜叠加变换将偏移距域共成像点道集转化为角度域共成像点道集.Sava和Fomel(2000，2003)又进一步区分了成像前与成像后提取ADCIGS(Angle domain common image gathers)，从而真正实现了角道集提取由叠后向叠前的转化.刘守伟等(2007)在均匀介质水平层反射情况下，对利用倾斜叠加方法提取的ADCIGS随偏移速度的变化进行了定量的分析，并把ADCIGS随偏移距变化的速度变化公式应用到了深度域层速度建模的流程当中，取得了很好的效果(张敏等，2007).

本文分析了前人的研究成果，针对角度域剩余曲率的分析方法，利用角度域共成像点道集建立了以剩余速度为自变量，剩余深度为目标函数的关系式，及以剩余深度为目标函数的梯度公式.利用导出的两个公式对剩余深度与剩余速度的关系进行了定量分析和模型试算.通过理论分析和模型试算证明初始速度模型的误差具有方向敏感性，正误差较负误差对速度建模迭代收敛更敏感.我们利用以上的结论进行速度建模既可以提高计算效率还可以提高偏移速度建模的精度.

2 剩余速度敏感性分析方法原理

2.1 角度域共成像点道集的抽取

无论是提取角度域共成像点道集的过程还是在角度域将波场进行延拓成像，本质都是将地震数据中的不同偏移距信息转化为不同的入射角信息的过程，这个过程消除了在偏移距域共成像点道集上由于多路径等因素引起的假象.

在地面观测条件下，如果不考虑回转波，地层倾角和入射角满足如下关系(Sava and Fomel,2003)：

(1)

式中：α为地层倾角；γ为局部入射角.

在波动方程偏移中，随着波动方程波场延拓，地面波场逐步向地下成像点移动，相应的成像空间偏移距逐步减小.当波场延拓到成像点附近时，局部偏移距分布在成像点附近很小的范围内，在此范围内可以认为速度是恒定不变的.在成像点附近有：

(2)

(3)

式(2)和式(3)中：s和r分别表示波场延拓至地下的局部源点和检波点的横向位置.v为地下反射点处的层速度.在该成像深度，中心点x和局部半偏移距h在地表满足：

(4)

(5)

根据式(2)、(3)、(4)和(5)有：

(6)

(7)

式(6)和式(7)中t表示走时，走时关于深度的导数满足：

(8)

根据式(7)和式(8)，可得(SavaandFomel, 2003)：

(9)

(9)式的傅里叶域算法等价于空间域的倾斜叠加运算，倾斜叠加算法在频率域就是一种简单的映射关系.通过(9)式的频率域倾斜叠加算法，就可以快速得到角度域共成像点道集.

局部偏移距等于0是波动方程单程波偏移的成像条件.如果速度真实准确，则不存在局部偏移距.只有当偏移速度不准确时才有局部偏移距的产生.把(9)式的局部偏移距h作为成像误差的输入，利用(9)式及时距曲线方程可以建立剩余深度、角度以及剩余速度之间的关系式.

2.2 角度域剩余深度与剩余速度关系建立

由于角度域共成像点道集能够避免多路径的假象问题，因此被认为是速度分析较为理想的道集.利用角道集既可以进行AVA(Amplitude-versus-Angle)属性反演，也可进行偏移速度分析.图1和图2分别描述的是当偏移速度小于真实速度，以及偏移速度大于真实速度时的局部偏移距观测系统，其反射点均不在真实的地层界面上.

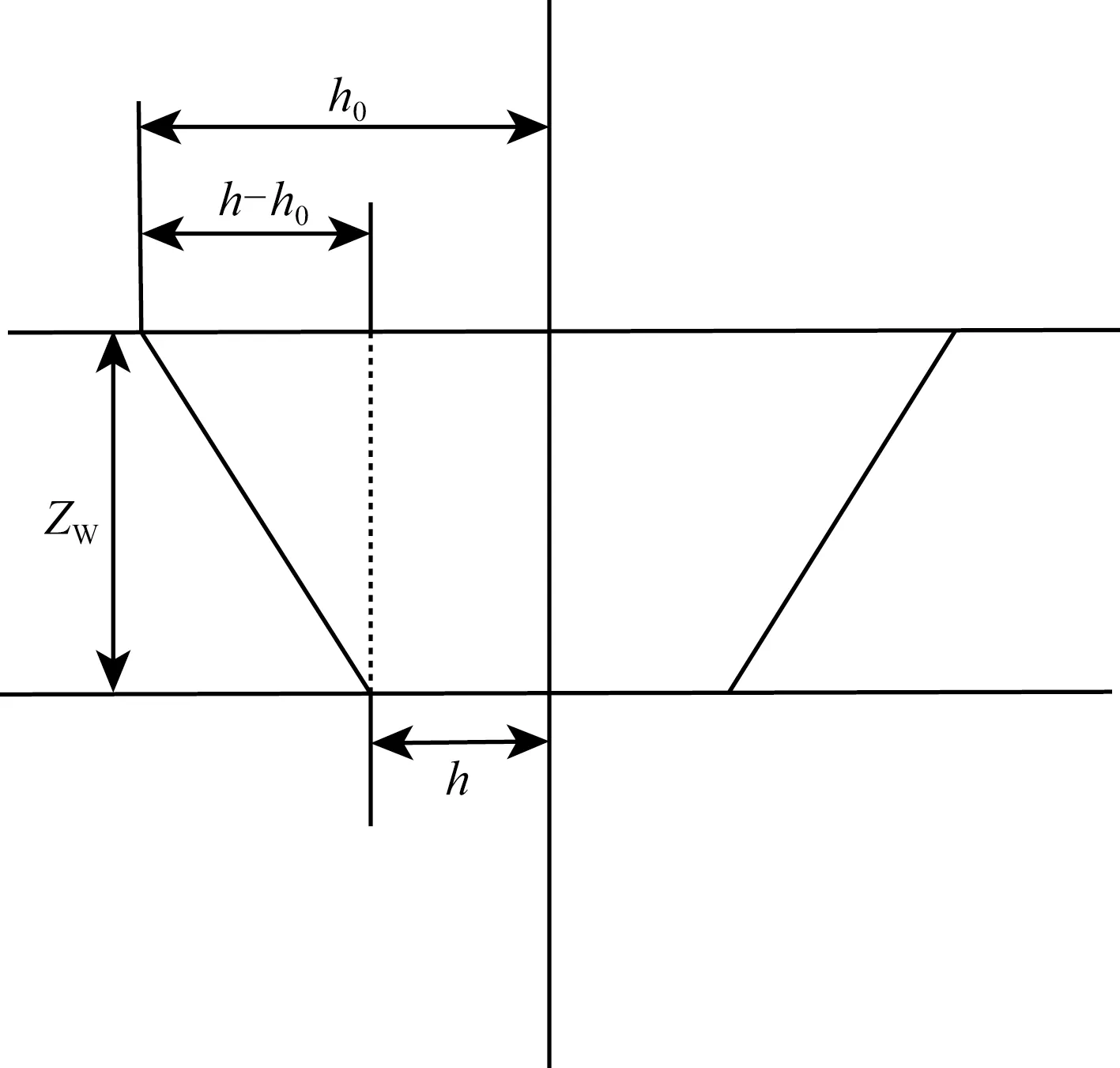
图1 速度偏小的观测系统Fig.1 Observation system speed is small

图2 速度偏大的观测系统Fig.2 Observation system speed is big

本文以图1所示的观测系统为例进行公式推导.真实反射界面为Z0，实际的聚焦深度为ZW，真实目标层速度为V0，地面偏移距为h0，零偏移距走时为t0，波场向下延拓的局部偏移距为h.当速度正确时，时距曲线关系式为：

(10)

当偏移速度不正确时，由上式可推断其时距曲线关系式为：

(11)

其中V为实际的偏移速度.

设偏移速度与真实速度误差为ΔV.当偏移速度偏差不大时，结合(10)式和(11)式，可得剩余速度与偏移深度之间的关系式(12)：

(12)

因为地表偏移距不随偏移深度变化，所以式(12)两边对h0求导，等式依然成立，得到地表偏移距与局部偏移距的关系式：

(13)

把方程(13)代入方程(12)可以消除地表偏移距：

(14)

(15)公式(15)两边对h求导，并反代入式(15)整理之后得：

(16)

剩余深度与剩余速度关系式为：

(17)

(17)式是以剩余速度ΔV为自变量，剩余深度ΔZ为目标函数的关系式.利用(17)式结合速度扫描的方法可以对深度域层速度进行迭代更新.其具体步骤为：在初始偏移结果的角道集上提取剩余深度.通过空间扫描的方法给定一系列的剩余速度值ΔV，利用这些剩余速度与提取出的剩余深度，结合(17)式可以正演出一系列的道集.把这些道集与偏移的角道集做互相关，相关性最好的道集对应的剩余速度即为应该校正的速度.

利用(17)式进行深度域速度更新，如需要考虑收敛的敏感性，应对(17)式求导即求目标函数的梯度，其结果如(18)式所示：

(18)

利用(17)和(18)式可以定量分析角度域剩余速度对剩余深度的敏感性.

2.3 剩余深度对剩余速度敏感性分析

对(17)式和(18)式做定量分析计算，并把所得的结果画成二维曲线图，其结果如图3a和3b所示.图3a中横坐标为剩余速度，纵坐标为剩余深度；图3b中横坐标为剩余速度，纵坐标为剩余深度的梯度值.每一条曲线代表一个角度值，从平缓的曲线到陡峭的曲线的角度取值范围分别从0°到45°.

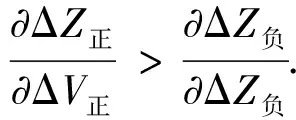
图3 (a)剩余速度与剩余深度关系； (b) 剩余速度与剩余深度的梯度值关系Fig.3 (a) Residual velocity and ADCIGS residual depth diagram; (b) Gradient diagram of residual velocity and residual depth

3 模型试算

3.1 水平层状介质模型

本文以单水平层状速度模型(如图4所示)为例进行剩余速度与剩余深度关系的模型试算.我们以该模型速度为基础，分别试算当上层速度保持不变(即真实速度)，速度增加200 m·s-1，以及速度减小200 m·s-1时的情况，生成的角度域共成像点道集结果如图5所示.

图4 单水平层状速度模型Fig.4 A single horizontal layered velocity model

如图5所示，当模型速度正确时，ADCIGS为一条水平的直线(图5a)；当上层速度增加200 m·s-1时，ADCIGS为一条下弯的曲线(图5b)；当上层速度减小200 m·s-1时，ADCIGS为一条上翘的曲线(图5c).对图5中三个道集进行比较可看出，偏大的剩余速度对应的剩余深度比偏小的剩余速度对应的剩余深度大很多.由此证实了速度正误差较负误差对于速度建模更敏感的理论分析.

下面对该模型进行速度更新试算：

我们先对剩余速度为-200 m·s-1的初始速度做一次速度更新，用更新之后的速度偏移并抽取ADCIGS，抽取的ADCIGS如图6所示.

此时的ADCIGS已近似逼近成水平直线，通常情况下，我们可以判断此时的目标层速度已经准确，此层的速度迭代应当终止.但把此时的偏移速度提取出来，剩余速度误差为-135 m·s-1，目标层的速度距离真实速度还有很大的偏差.

我们再用剩余速度为+200 m·s-1的初始速度做速度迭代，剩余速度同样更新到+135 m·s-1时，

图5 各速度抽取的角道集(a)正确速度；(b)速度加200 m·s-1；(c)速度减200 m·s-1.Fig.5 Angle gathers extracted from different velocities(a) The correct velocity ; (b) The correct velocity increased by 200 m·s-1 ; (c) The correct velocity decreased by 200 m·s-1.

图6 利用偏小的初始速度进行一次速度更新之后提取的ADCIGSFig.6 ADCIGS extraction after one time velocity update using the relatively small initial velocity

图7 利用偏大的初始速度进行一次速度更新之后提取的ADCIGSFig.7 ADCIGS extraction after one time velocity update using the relatively big initial velocity

此时的ADCIGS如图7所示.可以看出，此时的ADCIGS离水平直线还有很大的偏差，还需要继续进行速度更新才能得到更准确的速度.

由以上数值计算可以得出结论，若以偏小的初始速度进行速度迭代，则会产生由于其角道集剩余深度对剩余速度不敏感而导致速度迭代不充分的问题.若以偏大的初始速度进行速度迭代，则会避免该问题的产生.

图8 两层水平层状速度模型Fig.8 Two layers of horizontal layered velocity model

3.2 两层水平层状模型测试ADCIGS收敛的速度

本文以两层水平层状速度模型分别进行偏大和偏小初始速度收敛效率的对比测试，层速度模型如图8示.

下面我们分别试算当第二层速度保持不变(即真实速度)、第二层速度增加300 m·s-1、以及第二层速度减小300 m·s-1时的情况，生成的角度域共成像点道集结果如图9所示.由于第一层的速度并未发生改变，而第二层速度的改变对第一层对应的角道集不产生影响，因此该层对应的角道集为拉平的直线.而当第二层速度不变时，对应的ADCIGS为直线(图9a)；当第二层速度减小300 m·s-1时，对应的ADCIGS为上翘的曲线(图9b)；当第二层速度增大300 m·s-1时，对应的ADCIGS为下弯的曲线(图9c)，且曲线下弯的幅度比曲线上翘的幅度大.

应用公式(17)分别对剩余速度为+300 m·s-1和-300 m·s-1的初始速度做两次速度更新，剩余速度校正到+200 m·s-1，-200 m·s-1和+100 m·s-1，

图9 各速度抽取的角道集(a)真实速度；(b)速度减300 m·s-1；(c)速度加300 m·s-1.Fig.9 Angle gathers extracted from different velocities(a) The correct velocity; (b) The correct velocity increased by 300 m·s-1 ; (c) The correct velocity decreased by 300 m·s-1.

-100 m·s-1，它们对应的ADCIGS如图10和图11所示.

把两次更新的剩余深度分别做比较，如图12和图13所示

由两次剩余深度的更新比较中可看出，当更新的剩余速度值相同时，如果利用偏大的初始速度进行速度更新，剩余深度有更大的收敛值，从而说明利用偏大的初始速度进行速度更新比偏小的初始速度效率更高，收敛更快.

4 结论

为了使地震叠前深度域偏移速度建模方法具有更高的精度和效率，本文基于角度域共成像点道集建立了以剩余速度为自变量，剩余深度为目标函数的关系式，及剩余深度为目标函数的梯度公式.利用导出的两个公式对剩余深度与剩余速度的关系进行了定量分析和模型试算.通过定量分析和模型试算得出：初始速度模型的误差具有方向敏感性，利用偏大的剩余速度进行深度域速度更新，可以使迭代收敛效率更高，收敛的更加充分，从而使建模效率更高，最终的深度域速度模型更加精确.

图10 (a)剩余速度-200 m·s-1时偏移后提取的ADCIGS ；(b)剩余速度+200 m·s-1时偏移后提取的ADCIGSFig.10 (a) ADCIGS extraction after migration suing the residual velocity decreased by 200 m·s-1; (b) ADCIGS extraction after migration suing the residual velocity increased by 200 m·s-1

图11 (a)剩余速度-100 m·s-1时偏移后提取的ADCIGS；(b) 剩余速度+100 m·s-1时偏移后提取的ADCIGSFig.11 (a) ADCIGS extraction after migration suing the residual velocity decreased by 100 m·s-1; (b) ADCIGS extraction after migration suing the residual velocity increased by 100 m·s-1

图12 第一次更新剩余深度的比较Fig.12 The first update the residual depth comparison

图13 第二次更新剩余深度的比较Fig.13 The second update the residual depth comparison

Mackay S, Abma R. 1993. Depth-focusing analysis using a wavefront-curvature criterion.Geophysics, 58(8): 1148-1156.Al-Yahya K. 1989.Velocity analysis by iterative profile migration.Geophysics, 54(6): 718-729.Lee W B, Zhang L. 1992. Residual shot profile migration.Geophysics, 57(6): 815-822.Liu S W, Cheng J B, Wang H Z, et al. 2007. Relationships between offset domain/angle domain common image gathers and migration velocity.EarthScience-JournalofChinaUniversityofGeosciences

(in Chinese), 32(4): 575-582.Prucha M, Biondi B, Symes W. 1999. Angle-domain common image gathers by wave-equation migration. ∥ SEG Technical Program Expanded Abstracts, 824-827.Rickett J E, Save P C. 2002. Offset and angle-domain common image-point gathers for shot-profile migration.Geophysics, 67(3): 883-889.Sava P, Fomel S. 2000. Angle-gathers by Fourier transform.StanfordExplorationProject, 103: 391-401.Sava P C, Fomel S. 2003. Angle-domain common-image gathers by wavefield continuation methods.Geophysics, 68(3): 1065-1074.

Zhang M, Li Z C. 2007. Review of migration velocity model building.ProgressinExplorationGeophysics(in Chinese), 30(6): 421-427.

附中文参考文献

刘守伟, 程玖兵, 王华忠等. 2007. 偏移距域/角度域共成像点道集与偏移速度的关系. 中国科学-中国地质大学学报, 32(4): 575-582.

张敏, 李振春. 2007. 偏移速度分析与建模方法综述. 勘探地球物理进展, 30(6): 421-426.

(本文编辑 汪海英)

Sensitivity analysis of the residual depth about the residual velocity in the angle domain

XU Jia-Liang, CHANG Xu, WANG Yi-Bo

InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China

The velocity modeling in the depth domain is a key and difficult point in seismic data processing. In recent years, with the rapid development of pre-stack depth migration technology, the velocity modeling in the depth domain is becoming more and more important. Especially, the reverse-time migration method is developing very fast, but also hard to embody its advantages if there is no high accuracy of depth domain speed. So the accurate velocity model building is now a focused topic of active research.At present, in the industrial production, the tomographic technique is a most common method that is used in the depth domain velocity modeling. Firstly, it establishes an initial velocity model by using the speed coherent inversion method. Then it modifies the initial velocity model by using the error of the common reflection point gathers. This approach often requires taking the manual interaction, and the calculation precision is good. However, the conventional common reflection point in the offset domain has a maximum defect, namely there are many false appearances because of the multiple paths. Focusing on the tomographic technique in the depth domain velocity modeling, this paper establishes a relation with the residual velocity as the independent variable and the residual depth as the objective function. And a Gradient formula about the objedctive function is suggested by using the angle domain common image gathers to replace the conventional common reflection point gathers.We use this formula to make the quantitative analysis and model test for the relationship between the residual velocity and the residual depth. The theoretical analysis and model test demonstrate that the errors of initial velocity model have directional sensitivity. Based on the conclusions, the velocity model building can either increase the computational efficiency of migration velocity modeling, or improve the accuracy.The conventional velocity modeling process can be improved by the new cognition. Firstly, we make the initial velocity greater than the real speed. This process needs to take some manual intervention, namely this step is realized through manually jugging whether the gather is upward or downward. On this basis, we utilize the angle domain common image gathers to replace the offset domain common reflection point gathers, and then the initial velocity model can be updated by using the new formula. Tests on model data and real data indicate that the new method has great practical values.

Migration velocity analysis in depth domain; Angle domain common image gathers; Residual depth; Residual velocity

国家自然科学基金项目(41230317)，国家重大专项(2009CB219404)资助.

徐嘉亮，男，1985年生，博士，研究方向为地球物理.E-mail： 84829525@qq.com

10.6038/cjg20150825.

10.6038/cjg20150825

P631

2014-01-12，2015-06-30收修定稿

徐嘉亮, 常旭, 王一博. 2015. 角度域剩余深度对剩余速度的敏感性分析.地球物理学报，58(8):2927-2934,

Xu J L, Chuang X, Wang Y B. 2015. Sensitivity analysis of the residual depth about the residual velocity in the angle domain.ChineseJ.Geophys. (in Chinese),58(8):2927-2934,doi:10.6038/cjg20150825.