VTI地层随钻四极子声波测井数值研究

王瑞甲， 乔文孝*

1 中国石油大学油气资源与探测国家重点实验室, 北京 102249 2 北京市地球探测与信息技术重点实验室， 北京 102249



VTI地层随钻四极子声波测井数值研究

王瑞甲1,2， 乔文孝1,2*

1 中国石油大学油气资源与探测国家重点实验室, 北京 102249 2 北京市地球探测与信息技术重点实验室， 北京 102249

数值计算了四极子声源在含钻铤竖直向横向各向同性(VTI)地层井孔中产生的各种模式波的频散曲线、激发幅度以及对各地层、钻铤参数的灵敏度，合成了四极子阵列波形，研究了快、慢速地层井孔中地层各向异性的存在对四极子波场的影响.数值计算结果表明，地层各向异性对钻铤波的影响很小，对于地层波的影响较大，且影响因素非常复杂.仅在一些特殊的频率点处，地层模式波的控制因素相对较为简单，如螺旋波的截止频率处.在慢速地层井孔中，最低阶的地层四极子波对距离井壁约2个井孔半径内的地层有明显的响应，可以对该范围内的地层横波进行层析成像.在快速地层井孔条件下，可以考虑采用与横波到时相同的波包来评价地层横波信息.该波包包含了井孔折射横波、F1和F2模式与井孔折射横波速度相接近的部分；利用该波包获得的地层横波速度基本不受地层各向异性的影响.在慢速地层情况下，螺旋波受地层各向异性的影响较大，建议在实际数据处理时，考虑采用基于数据的处理方法进行频散校正.

四极子； 随钻测井； 声波测井； 横波

1 引言

随钻声波测井可以在钻进过程中提供实时的地层声学信息，在节约井口占用时间、规避风险等方面有着传统电缆测井不可比拟的优势(Tang and Cheng, 2004).早期的随钻声波仪器设计，照搬电缆测井已有的技术，未对含钻铤情况下的井孔波导做细致的分析，未能开发出成功的横波测量仪器.后来，人们逐步认识到了含钻铤井孔内钻铤波与地层波的耦合作用，认为四极子声源激发的螺旋波更适合随钻横波测量，并发展了采用四极子声源和接收器的随钻横波测井技术，实现了任意地层的随钻横波速度评价(Tang et al., 2002;Tang et al., 2003; Kinoshita et al.,2008;Zhang et al., 2010;Yang et al., 2011).在国内，目前随钻声波仪器的研发还处于起步阶段，迫切需要充分的理论研究和方法论证(肖红兵等, 2009; 卢俊强等, 2013).前人已经对随钻条件下多极子声源在井孔内激发的声场做了大量的研究，主要集中在井孔导波的模式分析(Tang et al., 2002;Tang et al., 2003; Wang and Tang, 2003; 王华等, 2009; Sinha et al., 2009；Sinha and Simsek, 2010;Geerits et al，2010; Wang and Tao, 2011; 李希强等,2013)，隔声体设计(杨勇等,2009;苏远大等,2011)以及物理模拟研究(Zhu et al., 2008;王兵等, 2012)等诸多方面.实际上，随钻四极子测井受到诸多因素的影响，目前的四极子随钻声波测井理论还不完备，在一些基本问题上还存在认识不清.这包括地层各向异性对随钻四极子波场中各模式的影响，快、慢速地层下随钻四极子波场的不同以及螺旋波的径向探测深度等问题.对这些问题的研究和分析，有助于完善随钻四极子横波测井的理论，为新一代的随钻声波测井仪器的设计提供必要的理论基础.本文建立了竖直向横向各向同性(VTI)地层竖直井随钻测井声学模型，数值计算了快、慢TI地层情况下四极子声源激励的声场，并尝试对上述问题进行了研究和解释.

2 VTI地层竖直井随钻测井声学模型

随钻测井声学模型可以用柱状径向分层声学模型来描述.图1为随钻测井声学模型示意图(Tang and Cheng, 2004;崔志文, 2004)，包括(a)模型的三维示意图和(b)井孔横截面示意图，S表示TI介质的对称轴，井轴与介质对称轴S平行.模型由内向外各介质依次为水眼(水)、钻铤、井孔(水)和地层，各介质的外径分别为r0、r1、r2和无穷大.井孔外地层为无限大TI介质.钻铤位于井孔中央，钻铤中间的水眼中充满水.特别地，在本文的讨论中，规定“井孔”为钻铤和地层之间的空间，并假设钻铤在井孔中

图1 VTI地层竖直井随钻测井声学模型示意图(a)及钻铤横截面示意图(b)Fig.1 Schematic diagram of acoustic model for logging while drilling in a VTI formation (a) and the cross section of a drill collar (b)

完全居中.

3 理论

3.1 井孔内外声场的解

在计算中，我们假设声源为安装在钻铤外壁的理想环状多极子声源.另外，假设水眼内代表沿径向向内传播的纵波的势函数的系数为Awh，钻铤内代表向内和向外传播的纵波和两种横波的势函数的系数分别为Aco、Bco、Cco、Dco、Eco和Fco，井孔中表示向内和向外传播的纵波的势函数的系数分别为Abh、Bbh，地层中表示向内和向外传播的纵波和两种横波的势函数的系数分别为Afo、Bfo、Cfo、Dfo、Efo和Ffo，缩写“co”、“wh”、“bh”、“fo”分别表示钻铤、水眼、井孔和地层.在柱坐标系(r,θ,z)下，根据水眼-钻铤、钻铤-井孔和井孔-地层处的边界条件(Tang and Cheng, 2004;崔志文, 2004)，得到

(1)

(2)

(3)

式(1)—(3)分别代表水眼-钻铤、钻铤-井孔、井孔-地层边界，其中u表示径向位移，p表示声压，τ表示应力.联立式(1)—(3)得到

M12×12X=S，

(4)

其中，

(5)

其中，f为井孔内流体的径向波数，Kn和In表示修正的贝塞尔函数，εn为多极子声源的权重因子，当n=0时，εn=1，当n>0时，εn=2.有关模型内各物理量及矩阵M的详细表达式，可参见文献(王瑞甲, 2012;李希强等, 2013).

通过对式的求解，可得到描述井孔内外声场的势函数的系数：

X=M-1S.

(6)

进一步，可以求得井内声场.与电缆测井的情况不同，在随钻测井中，采用两个势函数的系数来描述井孔声场.例如仪器外环上的声压场P如下(Tangetal., 2003)：

(7)

其中，ρf表示井孔流体密度，ω表示频率，S表示声源的子波函数.

3.2 模式波速度及激发强度

各模式波的速度、衰减由势函数系数的极点决定(Tang and Cheng, 2002)，即

(8)

式(8)又称作频散方程或者周期方程.该方程可以采用牛顿迭代法等数值方法求解，得到各模式波对应的轴向波数的极点ki，并进一步可得到模式波的传播速度vi=ω/ki.模式波的激发函数由极点对应的留数给出，根据留数定理可得

(9)

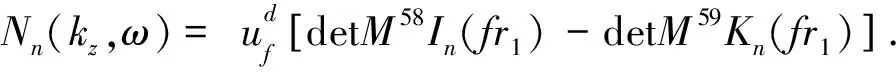
在TI介质井孔声场研究中，灵敏度分析是研究模式波速度受各地层参数控制程度的有效手段.对于随钻声波测井而言，灵敏度可以帮助分析模式波的类型及主要影响因素.模式波对于某参数P的灵敏度定义为归一化后的相速度对该参数的偏微分(Tang and Cheng, 2004)：

(10)

模式波速度对于径向上某位置上的某参数的灵敏度定义为(陈雪莲和王瑞甲, 2008)

(11)

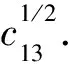
(12)

其中c11、c33、c44和c66表示地层刚性系数，ρ为地层的密度.

4 数值计算结果及分析

4.1 数值模型参数

计算中采用的TI地层的刚性参数如表1所示.

表1 地层参数Table 1 Formation parameters

表2 本文中井孔流体及钻铤的参数Table 2 Parameters of the borehole fluid and collar

本文中的快速、中速和慢速地层分别指其两种横波速度(vSH,vSV)均大于、接近或者小于井孔流体声速的地层.井孔内流体及钻铤参数见表2.计算采用的钻铤内半径、外半径及井眼半径分别为0.027 m、0.090 m和0.120 m.本文同时将TI地层计算结果与对应的各向同性地层计算结果进行了对比，用于参考的各向同性地层的声速选择为TI地层中沿旋转对称轴方向传播的纵、横波的速度，密度与TI地层相同.

4.2 快速地层

图2显示了快速地层情况下，四极子波的频散曲线和激发强度曲线.在计算的频率范围内观察到了四种模式，分别是地层螺旋波(F1、F2)、钻铤波(C1、C2).参照Sinha 等 (2009)，采用字符“C”和“F”的分别表示钻铤模式和地层模式，采用标识符“ISO”表示对应的各向同性地层.另外，在下面的频散曲线图中，实线表示相速度，虚线表示群速度.

从图2可见，地层四极子波(F1、F2)在截止频率处均趋近于地层沿竖直方向传播的横波速度vSV.螺旋波(F1)是强频散的模式，在截止频率处观察不到各向异性造成的速度的差异，而在稍高的频率下，可见各向异性地层螺旋波速度大于对应的各向同性地层的螺旋波.F2模式频散较弱.各向异性地层的F2模式截止频率小于各向同性地层；相同频率下，各向异性地层的F2模式的速度大于各向同性地层.未观察到地层各向异性对钻铤模式(C1、C2)的影响.从图2b可见，地层各向异性对地层波(F1、F2)的激发强度有轻微影响：F1模式各向异性地层和各向同性地层下的激发强度基本一致；对于F2模式，在17～27 kHz频率范围内，各向同性地层下的激发强度略大于各向异性地层的.地层各向异性对于钻铤模式(C1、C2)的激发强度基本不存在影响.

图3(a—d)分别是图2中F1、F2、C1和C2模式的灵敏度分析结果.从图3可见，钻铤模式波(C1、C2)基本上由钻铤纵波(vCP)、钻铤横波速度(vCS)、井孔流体速度(vBF)和钻铤内流体速度(vCF)控制，地层参数对其影响较小.地层螺旋波(F1)在截止频率处由沿竖直方向传播的横波速度(vSV)控制，而后随着频率增加，F1对于vSV的灵敏度下降很快，对其他地层参数和井孔流体速度的灵敏度先增加，后减小.高频处，F1模式主要为井孔流体速度(vBF)控制.F1模式对钻铤纵、横波速度不敏感，灵敏度小于0.1.F2模式在截止频率处也主要由vSV控制，随频率增加，vSV的控制缓慢地减弱，其他参数对F2的影响增加.一些学者提出了在快速地层中，采用F2模式而非F1模式来提取沿井轴方向传播的横波速度(Tang and Cheng, 2004)，主要基于F2模式频散较弱，而F1模式是强频散波的理论.从本文的结果可见，因为在F2模式的截止频率，除vSV的其他参数均对F2模式的速度影响较小(灵敏度均小于0.2)，采用F2模式波可以减小地层各向异性对于提取结果的影响.崔志文(2004)的理论模拟结果表明，在他的模型中，F2模式波的群速度和钻铤波的群速度相接近，钻铤波可能严重干扰F2模式的波形.实际上，钻铤波频散特征与钻铤尺寸有关：当钻铤外径不变，内径减小时，频散曲线向高频偏移，反之则向低频偏移(Tang et al., 2003; 崔志文, 2004).在实际仪器设计中，可选择合适的仪器结构尽量避开钻铤波的干扰.

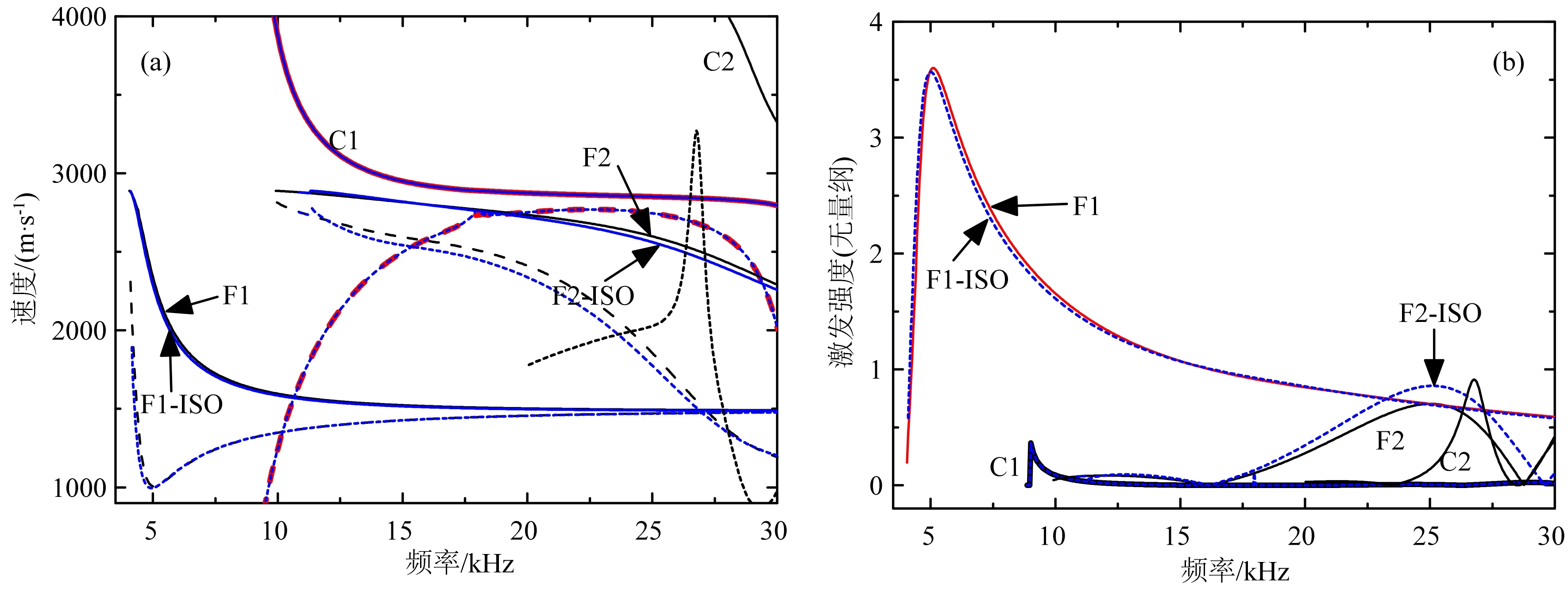
图2 随钻情况下快速VTI地层四极子声场模式分析，包括(a)频散曲线和(b)激发强度Fig.2 Mode analysis of quadrupole modes in a fast VTI formation, including (a) dispersion curves and (b) excitation intensity

图3 随钻情况下快速VTI地层四极子声场灵敏度分析，包括(a) F1、(b) F2、(c) C1、(d) C2Fig.3 Sensitivity analysis of quadrupole modes in a fast VTI formation, including (a) F1, (b) F2, (c) C1, (d) C2

4.3 中速地层

图4显示，在中速地层计算结果中观察到了地层螺旋波(F1)和钻铤波(C1)两种模式，而且钻铤波的频率远高于地层螺旋波激发的频率，地层螺旋波在截止频率处的速度为沿竖直方向传播的横波速度vSV.从图4a可见，各向异性地层螺旋波速度高于各向同性地层螺旋波速度，未观察到地层各向异性对C1模式波速度的影响.相比于各向同性地层(F1-ISO)，各向异性地层螺旋波(F1)激发强度的主频向高频偏移，激发强度略降低.

图5显示了图4中各模式波的灵敏度分析结果.螺旋波(F1)在低频处主要由沿竖直方向传播的横波速度vSV控制，而在稍高的频率内vPH、vSH和c13等对螺旋波速度都有一定的影响，说明此时地层各向异性对螺旋波有一定的影响，与图4一致.另外，地层螺旋波对钻铤纵、横波速度及钻铤内流体的速度的灵敏度基本为零，说明钻铤的弹性参数对地层螺旋波基本没有影响.从图5b可见，钻铤波(C1)基本由钻铤纵、横波速度控制，其他参数对其影响很小.4.4 慢速地层

图6是慢速地层四极子声源激发的各种模式波的频散曲线和激发强度曲线.在6a中，可观察到地层螺旋波(F1)、泄漏模式纵波(F2)和钻铤波(C1)三种模式波.地层模式波(F1、F2)受地层各向异性的影响较大：各向异性地层螺旋波速度大于各向同性地层，而泄漏模式纵波的速度小于各向同性地层.与中速地层一致，地层螺旋波在截止频率处的速度为沿竖直方向传播的横波速度vSV.钻铤波(C1)存在的频率高于地层螺旋波，未观察到地层各向异性对于钻铤波的影响.各向异性对于地层螺旋波的激发幅度有一定的影响，一方面各向异性地层螺旋波的激发的主频向高频偏移，另一方面激发强度较各向同性地层降低.

图4 随钻情况下中速VTI地层四极子声场模式分析，包括(a)频散曲线和(b)激发强度Fig.4 Mode analysis of quadrupole modes in a middle VTI formation, including (a) dispersion curves and (b) excitation intensity

图5 随钻情况下中速VTI地层四极子声场灵敏度分析，包括(a)F1、(b)C1Fig.5 Sensitivity analysis of quadrupole modes in a middle VTI formation, including (a) F1, (b) C1

图6 随钻情况下慢速VTI地层四极子声场模式分析，包括(a)频散曲线和(b)激发强度Fig.6 Mode analysis of quadrupole modes in a slow VTI formation, including (a) dispersion curves and (b) excitation intensity

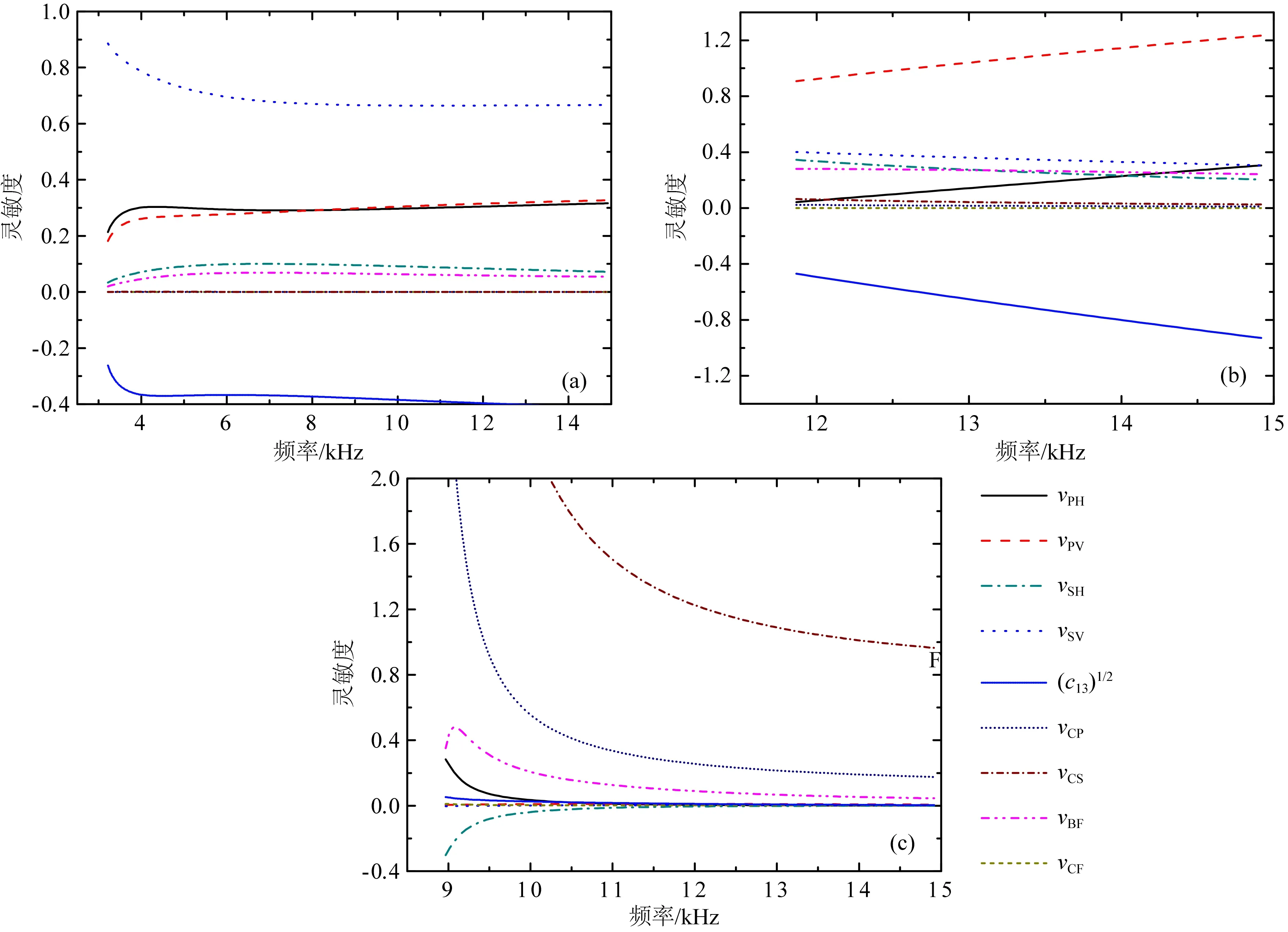
图7 随钻情况下慢速VTI地层四极子声场灵敏度分析，包括(a) F1、(b) F2、(c) C1Fig.7 Sensitivity analysis of quadrupole modes in a slow VTI formation, including (a) F1, (b) F2, (c) C1

图7显示了慢速地层中各模式波的灵敏度分析结果.由图7可见，低频螺旋波(F1)的速度由沿竖直方向传播的横波速度(vSV)控制，而在稍高的频率下，地层各参数及井孔流体参数均对地层螺旋波的速度有一定的影响.另外，地层螺旋波对于钻铤纵、横波速度及钻铤内流体速度不敏感.F2模式主要由沿竖直方向传播的纵波速度vPV和刚性系数c13控制，vSV、vSH、vBF以及vPH对其速度也有一定的影响.钻铤模式波(C1)主要由钻铤纵、横波速度控制，在9～10 kHz频率内沿水平方向传播的纵、横波速度对其有一些影响.

4.5 地层螺旋波的径向探测特性

图8(a—c)分别为快速地层、中速地层和慢速地层井孔中，地层螺旋波(F1)对于沿竖直方向传播的横波速度vSV的灵敏度.根据物理学的相似性原理，对于地层波而言，本征频率与井孔尺寸基本呈倒数关系，即缩小井半径，地层模式波的频散曲线、激发强度及灵敏度曲线向高频拉伸，反之则向低频压缩.因此，本文采用了井孔半径个数来表示径向灵敏度及其探测深度，以便于把结论推广到不同尺寸的井孔模型中.从图8(a—c)可见，距离井壁越远，地层螺旋波对于vSV的灵敏度越低，在截止频率附近，螺旋波对距离井壁大约2个井孔半径以内的地层有响应.相对于低频情况，在高频情况下，灵敏度随着径向距离的增加下降速度更快，这说明螺旋波基本呈现低频探测深，高频探测浅的特征.在4 kHz左右，快速地层中地层螺旋波对于vSV的灵敏度较高，而随频率增加很快降低，这是因为高频下的快速地层螺旋波的速度主要由井内流体速度控制.

可以根据径向灵敏度的计算结果来定量评价模式波的径向探测点(Investigation Position, IP).本文定义能够使得该径向位置之外的地层和该径向位置之内的地层对模式波的贡献相等的位置为模式波的径向探测点:

(13)

其中，rIP代表径向探测点距离井壁的距离，r为任意一点距离井壁的距离，Sen(r,ω)为径向灵敏度.图8d提取了各种地层情况下地层螺旋波(F1)的径向探测点.从图8d可见，中速地层低频螺旋波最深的径向探测点离井壁的距离约为0.8个井孔半径，而慢速地层为0.45个井孔半径，在8 kHz下两种地层的螺旋波的径向探测点距井壁的距离仅为0.1个井孔半径左右.

4.6 合成的阵列波形

利用式(7)合成井孔内接收的四极子波形，图9显示了不同频率下四极子声源在井孔内激发的声场，其中声源的子波函数为瑞克子波，接收器源距为2.0 m，S标识的直线表示横波的到时，(a)和(b)分别表示快、慢速各向同性地层.由图9a可见，观察到了多个波包，分别以符号W1、W2和W3标识.最先到达的为W1波包，到时与地层横波相同.结合图2结果可知，W1包含多种模式：井孔折射横波，F1模式截止频率处的部分和F2模式截止频率处的部分(10～12 kHz).由于这几种模式的群速度上几乎相同，在时域内重叠在一起，不能够分开.W2和W3波包在W1之后到达，主要为F1和F2模式中速度与地层横波速度差异较大的部分.综合图2和图9可知，W1波包能够较为准确地反应地层横波速度，无需进行频散校正等后续处理，是快速地层横波速度测量的首选.对比不同频率下的波形，可见，声源主频在8～12 kHz时，W1波包幅度较大，且受后续波影响较小，说明对于该地层，仪器合适的工作主频在8～12 kHz之间.另外，从图2也可以看到，在该频率范围内，钻铤波的群速度较小，不会影响W1波包.由图9b可见，在声源主频为2 kHz时，螺旋波(F1)波至点与地层横波相同，随着频率增加，螺旋波波至点逐渐后移.对于该模型而言，采用2 kHz的声源进行测量，可测得与地层横波速度最接近的螺旋波信号.在实际应用中，应综合考虑噪声、换能器特点等各种因素，选择合适的频率.

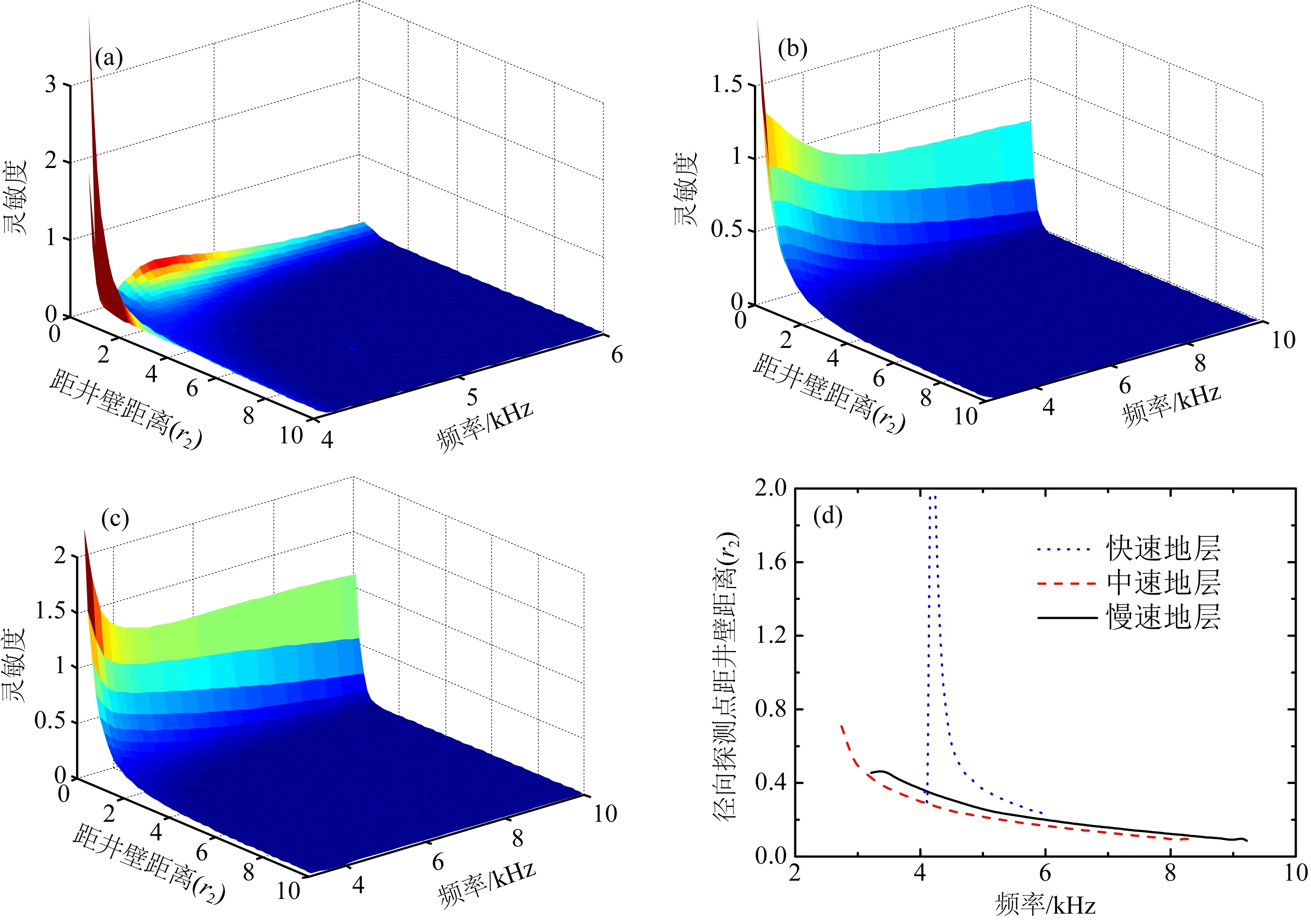
图8 随钻情况下(a)快速地层、(b)中速地层、(c)慢速地层中螺旋波的径向灵敏度及(d)径向探测点Fig.8 Radial sensitivity analysis of screw mode in a (a) fast, (b)middle, (c) slow formation and (d) the investigation depth of Stoneley mode

图9 不同频率下，四极子声源在快(a)、慢(b)地层井孔中产生的声场Fig.9 Acoustic wave field in fluid-filled borehole produced by a quadrupole source with different frequency

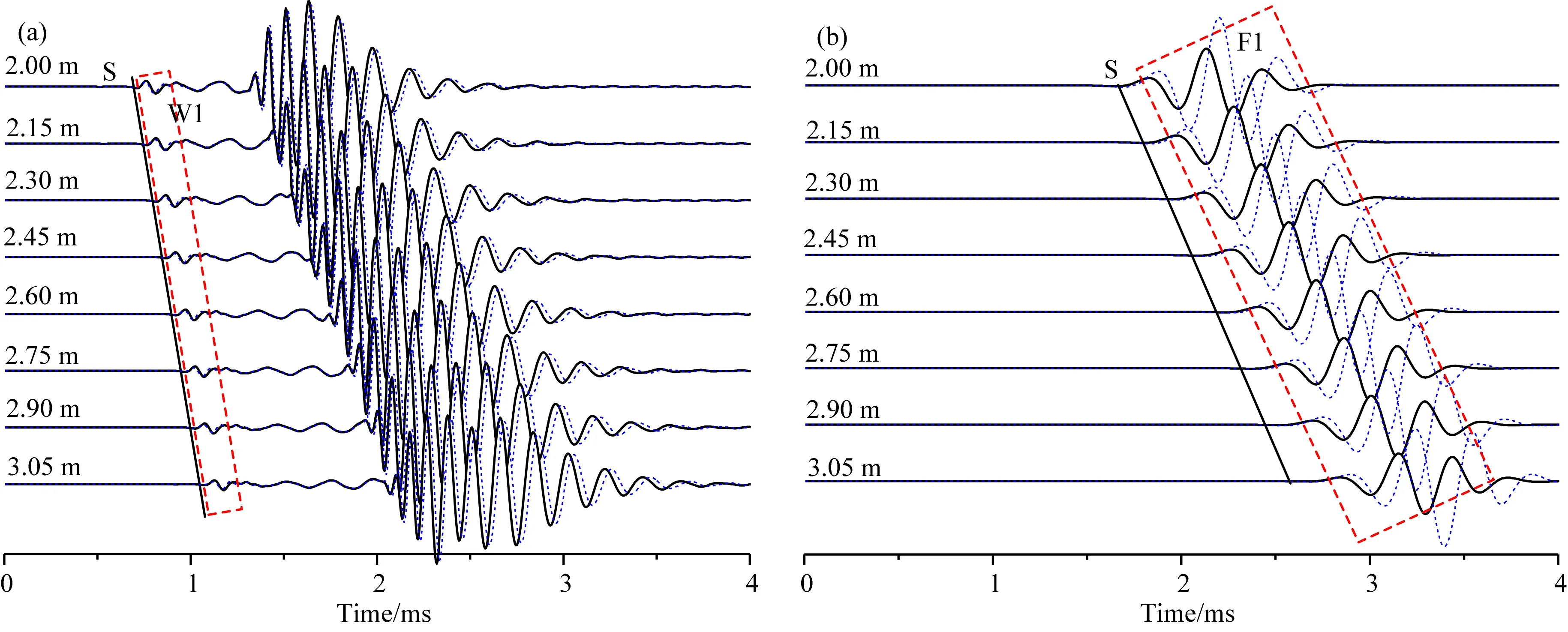
图10 四极子声源在各向异性地层与各向同性井孔中产生的声场的对比，包括(a)快速地层和(b)慢速地层Fig.10 Comparison of the waveforms between TI formations and corresponding isotropic formations produced by a quadrupole source, including (a) fast formation and (b) slow formation

图10对比了TI地层和各向同性地层情况下四极子声源在含钻铤井孔中产生的声场，其中实线表示TI地层计算结果，虚线表示对应的各向同性地层的计算结果.快、慢速地层采用的四极子源的主频分别为8和2 kHz.图10a显示，W1波包到时为地层横波到时，基本上不受地层各向异性的影响，能够准确反映地层的横波速度；后续波包受到了地层各向异性的影响，两种情况下的波形的相位有差别，幅度基本一致.从图10b可见，在慢速地层情况下，地层螺旋波的幅度和相位均受地层各向异性的影响较大.各向异性的存在使得F1模式到时提前，幅度降低，与图6中模式分析的结果相一致.

5 讨论

与偶极子声场不同，从四极子声场中各模式波的灵敏度分析结果可见，地层波基本不受钻铤弹性参数影响，钻铤波基本不受地层参数影响，未观察到地层波和钻铤波相互耦合的现象，与前人的结论一致(崔志文，2004; Sinha et al., ,2009;Geerits et al., 2010).地层各向异性对钻铤波的影响很小，对于地层波的影响较大，且影响因素非常复杂.对于本文研究的三种地层模型，仅在一些特殊的频率点处，地层模式波的控制因素相对较为简单，如螺旋波的截止频率.不过，虽然从这些频率点可以提取出不受地层各向异性影响的横波速度信息，但由于该频率下的模式波的激发幅度较小，波形信噪比较差，提取结果可能存在较大的误差.

螺旋波有着与电缆测井中的弯曲波(陈雪莲和王瑞甲, 2008)类似的径向探测特征：低频探测深、高频探测浅.与Su 等(2013)的结果不同，本文计算结果显示，对于本文的快速地层，由于稍高频率下螺旋波(F1)主要为井孔内流体的纵波速度控制，对地层横波速度不敏感，利用F1模式进行横波径向层析成像并不是一个好方法.对于慢速地层，由灵敏度分析结果可以看到，F1模式对约2个井孔半径内的地层有明显的响应，而且在计算的频率范围内，地层横波速度始终是最主要控制参数，可考虑利用其对地层横波速度进行层析成像.

对合成波形数据的分析表明，在快速地层条件下，W1波包可以给出准确的地层横波信息.需要注意的是，该波包包含了多种模式，包括井孔折射横波、F1模式和F2模式与井孔折射横波速度相接近的部分.结合灵敏度分析结果可知，W1波包基本不受地层各向异性的影响.另外，由于W1模式包含多种模式，其径向探测特征较为复杂.对于本文研究的模型，由于该波包的频率较高，其径向探测深度较浅.

在慢速地层条件下，低频地层螺旋波速度与地层横波速度接近，不受钻铤波影响，是软地层横波测量的首选模式.本文的计算结果显示，该模式受地层各向异性的影响较大.建议在实际处理中，如果考虑地层为各向异性地层，应避免采用依赖正演模型的方法(Kimball, 1998; Geerits and Tang, 2003; Wang et al., 2010)，可以考虑采用基于数据驱动的方法(Huang and Yin, 2005; Tang et al., 2010;孙志峰等, 2011)对螺旋波的低频趋势线进行估算.另外，上述的模拟结果显示，随钻四极子测井在快、慢速地层情况下的适用频率不同，在实际仪器设计中应考虑采用宽频带、大功率的发射器和高灵敏度的接收器，以提高采集数据的信噪比，扩大仪器测量的地层类型.

6 结论

数值研究了四极子声源在含钻铤TI地层中产生的声场，主要得到以下结论.

(1) 与偶极子声场不同，在四极子声源激发的模式波中未观察到地层波和钻铤波相互耦合的现象.地层各向异性对钻铤波的影响很小，对于地层波的影响较大，且影响因素非常复杂.仅在一些特殊的频率点处，地层模式波的控制因素相对较为简单，如螺旋波的截止频率处.

(2) 对于慢速地层，最低阶的地层螺旋波对距离井壁约2个井孔半径内的地层有明显的响应，有希望对该范围内的地层横波速度进行层析成像.

(3) 在快速地层井孔条件下，首至波包含了井孔折射横波、F1和F2模式中与井孔折射横波速度相接近的部分多种模式，其到时与横波的到时相同，可以用于准确提取地层横波速度.而且，利用该波包获得的地层横波速度基本不受地层各向异性的影响.

(4) 慢度地层螺旋波受地层各向异性的影响较大，建议实际数据处理时，如考虑地层为各向异性地层，应避免采用依赖正演模型的方法，可以考虑采用基于数据的处理方法.

致谢 美国壳牌国际石油公司黄山博士和中石化石油工程研究院吴金平博士对本文的完成提供了一些帮助，并提出了很好的建议和意见，在此表示感谢.

Chen X L, Wang R J. 2008. Investigating depth of mode waves in the borehole surrounded by transversely isotropic elastic formation.JournalofJilinUniversity(EarthScienceEdition) (in Chinese), 38(3): 502-507.Cui Z W. 2004.Theoretical and numerical study of modified Biot′s models, acousto-electric well logging and acoustic logging while drilling excited by multipole acoustic sources (in Chinese) [Ph. D. thesis]. Changchun: Jilin University.

Geerits T W, Tang X M, Hellwig O, et al. 2010. Multipole borehole acoustic theory: Source imbalances and the effects of an elastic logging tool.JournalofAppliedGeophysics, 70(2): 113-143.

Geerits T W, Tang X M. 2003. Centroid phase slowness as a tool for dispersion correction of dipole acoustic logging data.Geophysics, 68(1): 101-107.

Huang X J, Yin H Z. 2005. A data-driven approach to extract shear and compressional slowness from dispersive waveform data. ∥ SEG Technical Program Expanded Abstracts, 384-387.

Kimball C V. 1998. Shear slowness measurement by dispersive processing of the borehole flexural mode.Geophysics, 63(2): 337-344.

Kinoshita T, Takeshi T, Hiroshi N, et al. 2008. Next generation LWD sonic tool. ∥ 14th SPWLA Formation Evaluation Symposium of Japan, Japan.

Li X Q, Chen H, He X, et al. 2013. Analyses on mode waves of acoustic logging while drilling in transversely isotropic formations.ChineseJournalGeophysics(in Chinese), 56(9): 3212-3222, doi: 10.6038/cjg20130933.

Lu J Q, Ju X D, Qiao W X, et al. 2013. Application of digital signal processor to acoustic LWD tool.WellLoggingTechnology(in Chinese), 37(5): 527-530.

Sinha B K, Simsek E, Asvadurov S. 2009. Influence of a pipe tool on borehole modes.Geophysics, 74(3): E111-E123.

Sinha B K, Simsek E. 2010. Sonic logging in deviated wellbores in the presence of a drill collar. ∥ 2010 SEG Annual Meeting, Expanded Abstracts, Denver US, 553-557

Su Y D, Zhuang C X, Tang X M. 2011. LWD acoustic color mode wave attenuation character research and isolator design.ChineseJ.Geophys. (in Chinese), 54(9): 2419-2428, doi: 10.3969/j.issn.0001-5733.2011.09.026.

Su Y D, Tang X M, Zhuang C X, et al. 2013. Mapping formation shear-velocity variation by inverting logging-while-drilling quadrupole-wave dispersion data.Geophysics, 78(6): D491-D498.

Sun Z F, Fan G M, Meng J. 2011. A method of fitting function to extract phase slowness of dispersive wave from sonic logging data.JournalofJilinUniversity(EarthScienceEdition) (in Chinese), 41(4): 1239-1245.

Tang X M, Wang T, Patterson D. 2002. Multipole acoustic logging-while-drilling. ∥ 72nd Ann. Internat. Mtg., Soc. Explor. Geophys., Expanded Abstracts, 364-368.

Tang X M, Dubinsky V, Wang T, et al. 2003. Shear-velocity measurement in the logging-while-drilling environment: modeling and field evaluations.Petrophysics, 44(2): 79-89.Tang X M, Cheng C H. 2004. Quantitative Borehole Acoustic Methods. San Diego: Elsevier Science Publishing Co. Inc.

Tang X M, Li C, Patterson D J. 2010. A curve-fitting technique for determining dispersion characteristics of guided elastic waves.Geophysics, 75(3): E153-E160.

Wang B, Tao G, Chen T R, et al. 2012. Experimental study of acoustic logging while drilling measurements using an asymmetric source.ChineseJ.Geophys. (in Chinese), 55(1): 327-332, doi: 10.6038/j.issn.0001-5733.2012.01.033.

Wang H, Tao G, Wang B, et al. 2009. Wave field simulation and data acquisition scheme analysis for LWD acoustic tool.ChineseJ.Geophys. (in Chinese), 52(9): 2402-2409, doi: 10.3969/j.issn.0001-5733.2009.09.027.

Wang H, Tao G. 2011. Wavefield simulation and data-acquisition-scheme analysis for LWD acoustic tools in very slow formations.Geophysics, 76(3): E59-E68.

Wang T, Tang X M. 2003. LWD quadrupole shear measurement in anisotropic formations. ∥ Technical Program Expanded Abstracts, Dallas, Texas, 309-312.Wang R J, Qiao W X, Che X H. 2010. A new method of extracting

shear slowness from borehole mode waves. ∥ 2010 3rd International Congress on Image and Signal Processing (CISP), vol. 9, 4308-4312.Wang R J. 2012.Simulation research on acoustic logging in fluid-filled borehole surrounded by anisotropic formations (in Chinese) [Ph. D. thesis]. Beijing: China University of Petroleum.Xiao H B, Yang J Z, Ju X D, et al. 2009. Application of V-system in acoustic logging while drilling data denoising.JournalofChinaUniversityofPetroleum(EditionofNaturalScience) (in Chinese), 33(2): 58-62.

Yang Y, Che X H, Li J, et al. 2009. Sound isolation numerical simulation on isolator of logging while drilling sonic tool using finite difference time-domain method.JournalofChinaUniversityofPetroleum(EditionofNaturalScience) (in Chinese), 33(3): 66-70.Yang J Q, Sinha B, Valero H P, et al. 2011. Estimation of the formation shear and borehole fluid slownesses using sonic dispersion data in the presence of a drill collar. ∥ SEG Technical Program Expanded Abstracts, Vol. 30, 464-468.

Zhang Z X, Mochida M, Kubota M, et al. 2010. Shear slowness estimation by inversion of LWD borehole quadrupole mode. ∥SEG Technical Program Expanded Abstracts, 29: 528-532.

Zhu Z Y, Toksöz M N, Rao M, et al. 2008. Experimental studies of monopole, dipole, and quadrupole acoustic logging while drilling (LWD) with scaled borehole models.Geophysics, 73(4): E133-E143.

附中文参考文献

陈雪莲, 王瑞甲. 2008. 横向各向同性弹性地层井孔中模式波的探测深度. 吉林大学学报: 地球科学版, 38(3): 502-507.

崔志文. 2004. 多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究[博士论文]. 长春: 吉林大学.

李希强, 陈浩, 何晓等. 2013. 横向各向同性地层中随钻声波测井模式波分析. 地球物理学报, 56(9): 3212-3222, doi: 10.6038/cjg20130933.

卢俊强, 鞠晓东, 乔文孝等. 2013. 数字信号处理器在随钻声波测井仪中的应用. 测井技术, 37(5): 527-530.

苏远大, 庄春喜, 唐晓明. 2011. 随钻声波测井钻铤模式波衰减规律研究与隔声体设计. 地球物理学报, 54(9): 2419-2428, doi: 10.3969/j.issn.0001-5733.2011.09.026.

孙志峰, 樊官民, 孟杰. 2011. 一种提取声波测井频散波相慢度的适应函数方法. 吉林大学学报(地球科学版), 41(4): 1239-1245.

王兵, 陶果, 陈天润等. 2012. 非对称声源多极子随钻声波测井实验室测量研究. 地球物理学报, 55(1): 327-332, doi: 10.6038/j.issn.0001-5733.2012.01.033.

王华, 陶果, 王兵等.2009. 多极子随钻声波测井波场模拟与采集模式分析. 地球物理学报, 52(9): 2402-2409, doi: 10.3969/j.issn.0001-5733.2009.09.027.

王瑞甲. 各向异性地层声波测井模拟研究 [博士论文]. 北京: 中国石油大学, 2012.

肖红兵, 杨锦舟, 鞠晓东等. 2009. V 系统在随钻声波测井数据降噪中的应用. 中国石油大学学报(自然科学版), 33(2): 58-62.

杨勇, 车小花, 李俊等. 2009. 基于时域有限差分法的随钻声波测井仪隔声体隔声效果的数值模拟. 中国石油大学学报(自然科学版), 33(3): 66-70.

(本文编辑 胡素芳)

Numerical study on quadrupole acoustic LWD in VTI formations

WANG Rui-Jia1,2, QIAO Wen-Xiao1,2*

1StateKeyLaboratoryofPetroleumResourcesandProspecting,ChinaUniversityofPetroleum,Beijing102249,China2KeyLaboratoryofEarthProspectingandInformationTechnology,Beijing102249,China

Acoustic logging while drilling (LWD) is able to provide real-time acoustic properties of rock formations near bits, and therefore has an incomparable advantage over acoustic wireline logging (WL) in saving wellbore occupation time and avoiding risks. Current quadrupole acoustic LWD is capable of measuring formation shear velocity in arbitrary rock formations. However, the quadrupole acoustic LWD theory is not complete yet, i.e., there is no clear understanding on some fundamentals, which required further study.We derive the dispersion equations for the waveguide consisting of a fluid-filled borehole surrounded by a VTI formation, and numerically calculate the dispersion, amplitude and sensitivity functions of the borehole modes excited by a quadrupole acoustic source. We also synthesize the array waveforms recorded by the receivers in the borehole. The influences of formation anisotropy on borehole quadrupole modes are investigated.Numerical results show that, the formation anisotropy has negligible effects on the collar modes, while it strongly affects the formation modes. Only at a few frequencies, the control factor is simple, such as at the cut-off frequency of screw waves. The formation quadrupole modes of the lowest order show significant response to the formation shear velocity within approximate 2 borehole radii away from the sidewall, and it can be utilized to perform the radial tomography of shear velocity in this radial range. For fast formations, the first arrival includes borehole refracted shear mode, part of F1 and F2 modes, the velocities of which are close to that of shear modes, and it can be utilized to accurately evaluate the formation shear velocity without the influence of formation anisotropy. In slow formations, the formation screw modes are highly influenced by anisotropy.It suggests that, in field data processing, for fast formations, the first arrived wave packet can be utilized to extract shear wave velocity, while for slow formations, the formation screw waves can be processed by data-driven methods to obtain true shear wave velocity of rock formations. Because the operation frequencies for fast and slow formations are different, broadband and high-powered transmitters and high-sensitivity receivers should be adopted in the design of an acoustic LWD tool, to increase the signal-to-noise ratio and to improve application range of the tool.

Quadrupole； LWD； Acoustic logging； Shear waves

国家自然科学基金项目(11204380、11374371、11134011和61102102)，国家油气重大科技专项(2011ZX05020-009)，中国石油科技创新基金(2013D-5006-0304、2014D-5006-0307)和中国石油天然气集团公司项目(2014B-4011、2014D-4105、2014A-3912)联合资助.

王瑞甲，男，山东无棣人，汉族，博士，主要从事地球物理测井方法、检测声学等方面的研究工作.E-mail：wruijia@foxmail.com

*通讯作者乔文孝，男，山东禹城人，博士、博士生导师.研究方向：声波测井、检测声学. E-mail:qiaowx@cup.edu.cn

10.6038/cjg20150820.

10.6038/cjg20150820

P631

2014-06-21，2015-03-25收修定稿

王瑞甲，乔文孝. 2015. VTI地层随钻四极子声波测井数值研究.地球物理学报，58(8):2862-2872,

Wang R J, Qiao W X. 2015. Numerical study on quadrupole acoustic LWD in VTI formations.ChineseJ.Geophys. (in Chinese),58(8):2862-2872,doi:10.6038/cjg20150820.