航空电磁数据主成分滤波重构的噪声去除方法

王凌群， 李冰冰， 林君， 谢宾， 王琦， 程宇奇， 朱凯光

地球信息探测仪器教育部重点实验室，吉林大学仪器科学与电气工程学院， 长春 130026



航空电磁数据主成分滤波重构的噪声去除方法

王凌群， 李冰冰， 林君， 谢宾， 王琦， 程宇奇， 朱凯光*

地球信息探测仪器教育部重点实验室，吉林大学仪器科学与电气工程学院， 长春 130026

主成分分析方法利用低阶主成分重构航空电磁数据，解决了航空电磁探测中噪声与数据在频谱重叠情况下的噪声压制问题，但是参与重构的低阶主成分仍包含高频空间噪声，影响数据成像精度.本文提出的主成分滤波重构去噪方法，根据自适应窗宽平滑算法，设计了主成分低通滤波器组，对参与重构的低阶主成分进行测线滤波，再将滤波后的低阶主成分重构为电磁信号，不仅可以去除低阶主成分中的高频空间噪声，而且去除了高阶主成分包含的不相关噪声.仿真数据的去噪结果表明，主成分滤波重构获得较高的信噪比，较常规测线滤波与主成分重构分别提高了10.96 dB和2.52 dB；电导率深度成像结果证明了主成分滤波重构方法能够提高地下深部异常体的识别能力.最后通过实测数据的成像结果进一步验证了本文研究的主成分滤波重构去噪方法的有效性.

时间域航空电磁； 主成分； 滤波重构； 自适应窗宽； 空间噪声

1 引言

时间域航空电磁探测具有勘查速度快、探测范围广等优势，在我国具有广泛的应用前景.但是其机载的飞行探测方式，能够引起发射线圈、接收线圈晃动，同时飞行速度、飞行姿态等变化都能引起探测系统装置参数的不稳定，而且空中飞行探测过程中气压、温度等变化也能够引入系统电子参数改变，这些系统装置参数以及电子参数的变化都引入系统噪声，严重影响数据质量及成像精度，制约航空电磁探测系统对地下深部异常体及小异常体的反演解释，减小勘探深度.

常规数据处理，如时域叠加、频域滤波(Macnae et al.，1984；Buselli et al.，1998；Ridsdill and Dentith，1999；李楠，2009；吕东伟，2011)可以消除大部分随机噪声，但对于与信号频谱重叠的噪声却有很大的局限性(Lane et al，1998，2000).针对这一问题，20世纪90年代末期，国外学者利用数据的相关性，采用主成分分析法(Principal Component Analysis，PCA)研究数据的去除噪声方法.Jones 和 Levy(1987)利用相关性对数据进行降维压缩，去除了地震数据中的不相关噪声，提高了信噪比；Green(1998)利用主成分对图像信息进行降维压缩，提高了图像质量；主成分分析通过调整噪声的奇异值分解，去除了射线光谱中的噪声(Minty and Hovgaard，2002)；Qian和Fowler(2007)实现了光谱去相关以及光谱降维，提高了信息的保存性；主成分分析法不仅可以压制电磁数据中的噪声，还被运用到反演计算中(Kass and Li，2007；Kass et al.，2010)；2011年，PCA被应用去除心电信号中的伪影和噪声，有效地提取有用的心电信号(Chawla，2011).近年来，我国学者也开始将主成分分析方法引入到数据处理中，利用PCA去除高光谱遥感数据噪声(常威威等，2009)；利用主成分分析法成功地压制了乘性噪声(姚莉丽等，2011)；Zhu等(2012)将主成分引入到航空电磁数据的反演中，在噪声数据的反演解释中，取得了优于其他反演方法的结果；2013年，主成分分析法应用于航空电磁数据的噪声处理中，解决了由于噪声与数据的时频特性重叠而带来的去噪困难的问题(朱凯光等，2013).

上述主成分分析去噪方法，均是将数据转化成一组按方差由大到小排列的不相关的主成分，采用少量低阶主成分重构原数据，从而去除高阶主成分包含的不相关噪声.但是，这些参与重构的低阶主成分中仍然包含一定程度噪声(朱凯光等，2013，图2)，对数据的精细处理与信息提取影响很大.

针对这一问题，本文提出基于主成分滤波重构的航空电磁数据去噪方法，首先分析了参与重构测线数据的低阶主成分中的高频空间噪声特点，研究了自适应窗宽的低通滤波器，设计了主成分低通滤波器组，并详细给出了主成分滤波重构算法，最后通过仿真数据和实测数据的主成分滤波重构去噪实例，结合电导率深度成像结果对比，验证了本文去噪算法的有效性.

2 主成分滤波去噪方法

文献(朱凯光等，2013)给出的主成分噪声去除结果表明，主成分重构去噪方法虽然去除了高阶主成分中的不相关噪声，但是参与重构的低阶主成分仍将其包含的高频空间噪声引入测线数据.

2.1 主成分滤波的去噪原理

基于主成分重构去噪方法，本文首先对参与重构的低阶主成分沿测线低通滤波，再进行航空电磁数据重构，不仅能够去除高阶主成分中包含的不相关噪声，而且能有效地压制低阶主成分中的高频空间噪声.

设航空电磁探测某m道n个测点的测线数据为X(m×n)，利用文献(朱凯光等，2013)中的式(1)—(3)，计算其自相关阵的特征向量矩阵R(m×m)、特征值矩阵λ(m×1)，得到测线数据n个测点的m个主成分Ψ(m×n).根据式(1)计算前p个主成分的累计贡献率δp为

(1)

式中，λk为第k阶主成分对应的特征值.当前p个主成分的累计贡献率高于95%时，选p为重构电磁信号的低阶主成分个数.

(2)

那么，滤波后的第k阶主成分可表示为

(3)

同样，根据式(2)和式(3)可得到低通滤波器组滤波后的前p个低阶主成分的剖面数据，则滤波后的主成分矩阵为

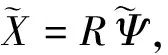
(4)

2.2 主成分滤波器设计

(5)

(6)

根据各测点的自适应窗宽Wk(j)，得到第k阶主成分滤波器的单位冲激响应函数hk(j)为(郑君里等，2000)

(7)

式中j=1,2,…,n.

但是对剖面曲线起始和尾部测点进行滤波时，为避免滤波点数不足，窗宽采用下式计算：

Wk(j)=

(8)

本文采用自适应窗宽平滑算法设计的主成分低通滤波器组，能够根据信号的局部特性自适应地改变滤波器频带，比常规固定带宽的低通滤波器具有明显优势，不仅能够有效去除主成分剖面的高频空间噪声，还可以保证主成分异常的幅度.但是，最佳滤波参数的确定尤为重要，滤波过度导致剖面弱异常被滤掉，而欠滤波会导致噪声过大而形成深部假异常.因此，不仅要根据实测数据处理经验、当地地质条件，还要根据电磁数据剖面异常形态甚至是各测点的off-time段衰减曲线特征，反复调整才能确定最佳滤波参数.

3 仿真数据的去噪实例

3.1 时间域航空电磁探测系统的仿真数据

为评价主成分滤波重构去噪效果，特别是晚期道的噪声水平，本文设计了含有深部异常体的准二维大地模型，如图1所示，在电导率为0.02 S·m-1的均匀半空间模型400 m深处，有一个厚50 m、长1 km的异常体，测点间隔5 m，测线共有1000个测点.

时间域航空电磁探测系统为中心回线方式，发射线圈半径为7.5 m，飞行高度为25 m，发射波形为基频25 Hz的正负方波，电流强度归一化为1 A (实际发射电流一般为300～500 A)，经正演计算(朱凯光等，2010；殷长春等，2013)，得到各测点的17道(0.2～10.76 ms)off-time段电磁响应，剖面曲线如图2中蓝色线所示.为仿真野外实测数据，在正演数据中加入含基频的复杂噪声，形成的剖面曲线如图2中红色线所示.

由图2可以看到，正演数据(蓝色线)的剖面曲线在第400～600测点处存在明显的晚期异常，与理论模型的深部异常体一致；而含噪数据(红色线)晚期道的异常几乎被噪声淹没，无法有效地反映地下深部异常体.

3.2 主成分滤波去噪结果分析与对比

采用文献(朱凯光等，2013)中的式(1)—(3)分别计算正演数据和含噪数据的17个主成分，前两个低阶主成分的累计贡献率约为99%，因此选择第1与第2阶主成分重构电磁数据.正演数据与含噪数据的第1与第2阶主成分如图3中的蓝色线和红色线所示.

可以看到，含噪数据主成分的剖面数据(红色线)包含高频空间噪声，如第1阶主成分噪声幅度的峰峰值约为0.005 nT·s-1.针对主成分剖面中的噪声，本文采用自适应窗宽滤波器，对参与重构的第1、第2阶主成分分别进行测线滤波.设计滤波器的最大窗宽为51，最小窗宽为3，各主成分剖面数据的滤波结果如图3中的绿色线所示.滤波后主成分剖面噪声明显减小，与正演数据主成分剖面基本一致.

图1 准二维大地模型示意图Fig.1 Sketch of a pseudo-2D earth model

为对比去噪效果，本文分别采用常规测线滤波、主成分重构和主成分滤波重构对仿真数据进行去噪处理，图4给出了三种方法去噪后电磁数据的后四道剖面曲线.

对比图4a、4b和4c可以看到，经常规测线滤波处理后的剖面曲线(图4a)的晚期道数据无明显异常，无法反映大地模型的深部异常体；主成分重构去噪处理(图4b)的后四道剖面数据能够基本恢复原剖面数据，但仍有高频残余噪声，影响晚期道异常的

图2 准二维大地模型的17道电磁数据剖面曲线Fig.2 A 17-channel profile of the pseudo-2D earth model

图3 准二维大地模型的主成分剖面曲线(a) 第1阶主成分剖面曲线； (b) 第2阶主成分剖面曲线.Fig.3 Profiles of PCs for the pseudo-2D earth model(a) Profile of PC1； (b) Profile of PC2.

图4 准二维大地模型的后四道剖面曲线去噪结果对比(a) 常规测线滤波结果; (b) 主成分重构结果; (c) 主成分滤波重构结果.Fig.4 Comparison of the last 4-channel profiles denoised by different methods for the pseudo-2D earth model(a) By filtered traditional profile；(b) PC reconstruction；(c) By filtered PC reconstruction.

图5 去噪后的电导率深度成像结果对比图(a) 常规测线滤波结果; (b) 主成分重构结果; (c) 主成分滤波重构结果.Fig.5 CDI comparison for the pseudo-2D model with data processed by three denoising methods(a) By filtered traditional profile；(b) PC reconstruction；(c) By filtered PC reconstruction.

图6 河南野外航空电磁探测的17道剖面曲线Fig.6 Seventeen-channel profiles of field data from airborne time domain electromagnetic survey in Henan Province

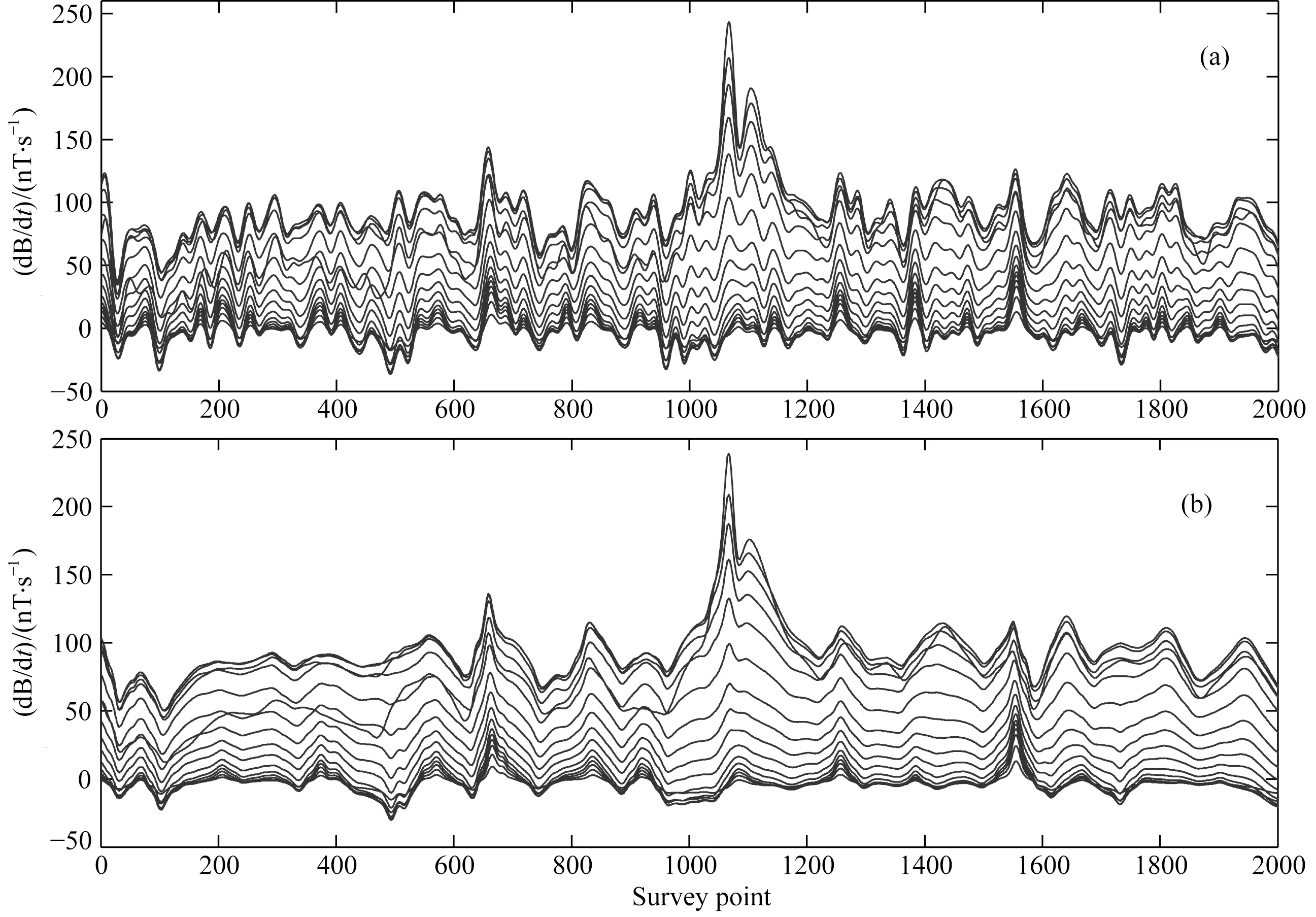
图7 实测数据去噪后电磁数据剖面曲线(a) 主成分重构; (b) 主成分滤波重构.Fig.7 Profiles after noise removal for survey data in Henan Province(a) PC reconstruction; (b) By filtered PC reconstruction.

图8 实测数据去噪后电导率深度成像对比图(a) 常规低通测线滤波; (b) 主成分重构; (c) 主成分滤波重构.Fig.8 CDI comparison for field data denoised by different methods(a) By filtered traditional profile；(b) PC reconstruction；(c) By filtered PC reconstruction.

识别；而主成分滤波重构处理(图4c)后的晚期道数据不仅可以清晰地看到异常位置，而且保证了异常的幅值，噪声幅值明显减小，信噪比较常规测线滤波提高了10.9633 dB，较主成分重构提高了2.5234 dB.3.3 电导率深度成像结果对比

图5分别给出了三种方法处理后的剖面数据的电导率深度成像(Conductivity-Depth Imaging，CDI)结果，常规测线滤波处理的数据CDI结果(图5a)不能有效反映深部异常体位置，异常体沿测线出现横向扩散，甚至有部分区域出现伪异常；主成分重构去噪的CDI结果(图5b)，能够较清晰地看到深部异常体，但同深度由于残余噪声沿测线仍出现小部分异常扩散；而主成分滤波重构去噪的CDI结果(图5c)效果明显，与理论模型接近，表明该方法有较强压制噪声能力，较其他两种方法具有更好的成像精度.可见，本文提出的主成分滤波重构算法能够提高航空电磁探测对深部异常体的识别能力.

4 实测数据的去噪实例

4.1 实测剖面数据的去噪结果对比

2012年4月，国土资源部航空物探遥感中心与吉林大学合作研制开发的我国首套完整吊舱式时间域直升机航空电磁探测系统，在河南省某地勘查测量.该地区地质结构显高阻特性，电阻率约为3000～8000 Ωm，电磁响应幅值较小.本文以河南野外实验中某条测线的17道(0.2～10.76 ms)剖面数据为例，常规测线滤波处理的剖面数据如图6所示，在测点1100附近有幅值约为200 nT·s-1的异常.

对该测线的剖面数据进行主成分重构与主成分滤波重构的去噪处理，结果分别如图7a和图7b所示.对比图6和图7，可以看到本文研究的主成分滤波重构算法取得了最好的去噪结果(图7b)，去除了测线上的高频空间噪声，有助于对深部异常体的识别.

4.2 电导率深度成像结果对比

对三种方法去噪后的电磁数据(图6、图7a和图7b)分别进行电导率深度成像，结果分别如图8a、图8b和图8c所示.可以看到，三种数据去噪方法都能明显显出第1100测点处的异常体，但是常规测线滤波处理的数据成像结果(图8a)还显示，在地下深部450 m处存在几乎连成一层的低阻异常，无法准确的圈定地下异常体位置；主成分重构处理的结果也出现了不同程度的低阻异常扩散现象，与当地的高阻地质情况不符，是测线高频空间噪声所致；但是主成分滤波重构的CDI结果(图8c)显示，本文研究算法有效地压制了测线高频噪声，并保持测线异常幅度，获得清晰的电导率成像结果.

5 结论

(1)本文将航空电磁数据噪声处理变换到主成分域中进行，经主成分分解、去噪、再重构，既滤除了低阶主成分中的高频空间噪声，又去除高阶主成分中的不相关噪声.主成分滤波重构去噪方法不仅可以提高数据晚期道的信噪比，而且增强了航空电磁探测系统对深部异常体的分辨能力，并成为时域、频域噪声处理方法的重要补充，为地球物理探测数据的变换域分解与合成以及噪声处理等方面提供了新思路.

(2)本文采用自适应窗宽滤波算法，设计的低通滤波器组能够根据航空电磁数据各阶主成分剖面数据的局部变化特征，自适应地改变滤波器的带宽，不仅可以有效地滤除主成分的高频空间噪声，而且有效地保持了异常的幅值，具有优于常规低通滤波器的滤波性能.该滤波算法也可有效地用于测线电磁数据的滤波.

致谢 衷心感谢吉林大学地球信息探测仪器教育部重点实验室为本文提供的吊舱式时间域直升机航空电磁探测系统的实测数据，感谢吉林大学时间域航空电磁组的全体成员对此文的帮助和指导.

Buselli G, Hwang H S, Pik J P. 1998. AEM noise reduction with remote referencing.ExplorationGeophysics, 29(2): 71-76.

Chang W W, Guo L, Liu K, et al. 2009. Denoising of hyperspectral data based on contourlet transform and principal component analysis.JournalofElectronics&InformationTechnology(in Chinese), 31(12): 2892-2896.

Chawla M P S. 2011. PCA and ICA processing methods for removal of artifacts and noise in electrocardiograms: A survey and comparison.AppliedSoftComputing, 11(2): 2216-2226.

Green A. 1998. The use of multivariate statistical techniques for the analysis and display of AEM data.ExplorationGeophysics, 29(2): 77-82.

Jones I F, Levy S. 1987. Signal-to-noise ratio enhancement in multichannel seismic data via the karhunen-loéve transform.GeophysicalProspecting, 35(1): 12-32.

Kass M A, Li Y G. 2007. Use of principal component analysis in the de-noising and signal-separation of transient electromagnetic data. The 3rdInternational Conference on Environmental and Engineering Geophysics (ICEEG). Wuhan, China. Kass M A, Li Y G, Krahenbuhl R, et al. 2010. Enhancement of TEM data and noise characterization by principal component analysis. Douglas Oldenburg: Department of Geophysics Colorado School of Mines.Lane R, Green A, Golding C, et al. 2000. An example of 3D conductivity mapping using the TEMPEST airborne electromagnetic system.ExplorationGeophysics, 31(2): 162-172. Lane R, Plunkett C, Price A, et al. 1998. Streamed data—a source of insight and improvement for time domain airborne EM.ExplorationGeophysics, 29(2): 16-23.

Li N. 2009. Research on Airborne time-domain electromagnetic data preprocessing [Master thesis] (in Chinese). Changchun: Jilin University.

Lü D W. 2011. Methods study of helicopter-borne towed bird time domain electromagnetic data processing [Master thesis] (in Chinese). Chengdu: Chengdu University of Technology. Macnae J C, Ltagne Y, West G F. 1984. Noise processing techniques for time-domain EM systems.Geophysics, 49(7): 934-948.Minty B, Hovgaard J. 2002. Reducing noise in gamma-ray spectrometry using spectral component analysis.ExplorationGeophysics, 33(4): 172-176. O′Connell M D. 2010. Adaptive width filters for GEOTEM data. Canada, Ottawa: Consultant to Fugro Airborne Surveys.

Qian D, Fowler J E. 2007. Hyperspectral image compression using

JPEG2000 and principal component analysis.IEEEGeoscienceandRemoteSensingLetters, 4(2): 201-205.

Ridsdill-Smith T A, Dentith M C. 1999. The wavelet transform in aeromagnetic processing.Geophysics, 64(4): 1003-1013.

Yao L L, Feng X C, Li Y F. 2011. Principal component analysis method for muitiplicative noise removal.ActaPhotonicaSinica(in Chinese), 40(7): 1031-1035.

Yin C C, Huang W, Ben F. 2013. The full-time electromagnetic modeling for time-domain airborne electromagnetic system.ChineseJournalofGeophysics(in Chinese), 53(3): 743-750, doi: 10.6038/cjg20130928.

Zheng J L, Ying Q H, Yang W L. 2000. Signals and Systems (in Chinese). Beijing: Higher Education Press.

Zhu K G, Lin J, Han Y H, et al. 2010. Research on conductivity depth imaging of time domain helicopter-borne electromagnetic data based on neural network.ChineseJournalofGeophysics(in Chinese), 53(3): 743-750, doi: 10.3969/j.issn.0001-5733.2010.03.030.

Zhu K G, Ma M Y, Che H W, et al. 2012. PC-based artificial neural network inversion for airborne time-domain electromagnetic data.AppliedGeophysics, 9(1): 1-8. Zhu K G, Wang L Q, Xie B, et al. 2013. Noise removal for airborne electromagnetic data based on principal component analysis.TheChineseJournalofNonferrousMetals(in Chinese), 23(9): 2430-2435.

附中文参考文献常威威, 郭雷, 刘坤等. 2009. 基于Contourlet 变换和主成分分析的高光谱数据噪声消除方法. 电子与信息学报, 31(12): 2892-2896. 李楠. 2009. 时间域航空电磁数据预处理技术研究[硕士论文]. 长春: 吉林大学.

吕东伟. 2011. 吊舱式时间域直升机航空电磁数据处理方法研究[硕士论文]. 成都: 成都理工大学.

姚莉丽, 冯象初, 李亚峰. 2011. 去除乘性噪音的主成分分析算法. 光子学报, 40(7): 1031-1035.

殷长春, 黄威, 贲放. 2013. 时间域航空电磁系统瞬变全时响应正演模拟. 地球物理学报, 56(9): 3153-3162, doi: 10.6038/cjg20130928. 郑君里, 应启珩, 杨为理. 2000. 信号与系统. 北京: 高等教育出版社. 朱凯光, 林君, 韩悦慧等. 2010. 基于神经网络的时间域直升机电磁数据电导率深度成像. 地球物理学报, 53(3): 743-750, doi: 10.3969/j.issn.0001-5733.2010.03.030.

朱凯光, 王凌群, 谢宾等. 2013. 基于主成分分析的航空电磁数据噪声去除方法. 中国有色金属学报, 23(9): 2430-2435.

(本文编辑 张正峰)

Noise removal based on reconstruction of filtered principal components

WANG Ling-Qun， LI Bing-Bing， LIN Jun， XIE Bin， WANG Qi， CHENG Yu-Qi， ZHU Kai-Guang*

KeyLaboratoryofGeo-ExplorationInstrumentation,MinistryofEducation,JiLinUniversity，Changchun130026，China

Airborne electromagnetic data has complex noise due to the flight environment, changes of system parameters and device parameters. The traditional time-frequency approach is difficult to remove noise. PCA (principal component analysis) can remove the noise which overlaps with the signal frequency spectrum. However the low-order components still contain high frequency spatial noise. To solve this problem, this work proposes the reconstruction of filtered principal components which can not only remove the high-frequency spatial noise of low-order components, but also remove uncorrelated noise of high-order components.This approach uses filtered principal components to reconstruct electromagnetic data. Firstly, it computes eigenvectors and eigenvalues matrix of the correlation matrix and the principal component profiles which are uncorrelated. The low-order principal components associated with the big eigenvalues reflect the correlated electromagnetic signals, while high-order principal components associated with the small eigenvalues are corresponding to the uncorrelated noise. It operates by first filtering the principal component profiles with the widest filter. Then according to local variation of each smoothed principal component profile, a group of low-pass filters is designed. Local variation of each smoothed principal component profile is converted linearly into adaptive smoothing filter window width of the measuring point. So each principal component profile is filtered by the corresponding filter. Finally, filtered low-order principal components are used to reconstruct electromagnetic signal.This paper designed a pseudo-2D earth model with a deep target. The noise added to it drowned the target of later channels and the CDI (conductivity depth imaging) cannot reflect the deep target. After PCA processing, principal component profiles of noise-contaminated data have high frequency spatial noise compared with those of the forward data. The peak to peak of noise amplitude of the first principal component is about 0.005 nT/s. With an adaptive window wide filter, noise of the principal component profile is significantly reduced and consistent with the forward data mostly. The data is processed by three de-noising methods. The later channels profiles by the traditional profile filter have no obvious target and CDI cannot reflect the deep target either. The later channels profiles by principal component reconstruction still contain high frequency noise, impacting identification of the deep target. But data by filtered principal component reconstruction not only eliminates high frequency noise, but also ensures the magnitude of the target. It shows the more accurate position and shape. SNR is improved by 10.96 dB and 2.52 dB relative to the other two methods.This work deniosed one survey line measured in Henan Province. The CDI results of other two methods exhibit low-resistance target diffusion phenomenon to different degrees and cannot show exact location of the target for this survey line. But the CDI by filtered principal component reconstruction indicates that the algorithm in this paper can suppress high frequency noise effectively, consistent with real local condition.ATEM data is converted into the principal component domain. A group of low-pass filters is able to change the filter bandwidth adaptively according to local variation of each principal component profile. It can not only filter out high frequency spatial noise, but also maintain the target amplitude. At the same time, it also improves the SNR of latest channel data and enhances the ability to identify the deep target after filtered principal component reconstruction. Filtered principal component reconstruction is an important complement to noise processing of time and frequency domain, providing a new line of thought for decomposition and synthesis of the transform domain and de-noising processing of geophysical data.

Time-domain airborne electromagnetism； Principal component analysis； Reconstruction after filtering； Adaptive width algorithm； Spatial noise

国家高技术研究发展计划项目(2013AA063904),国家自然科学基金项目(41274076)和国家重大科研装备研制项目(ZDYZ2012-1-03)联合资助.

王凌群，女，1988年生，吉林大学博士研究生，研究方向为航空电磁数据处理与噪声压制. E-mail:399127431@qq.com

*通讯作者朱凯光，女，1970年生，吉林大学教授，博士生导师，研究方向为电磁探测技术与信号处理. E-mail:zhukaiguang@jlu.edu.cn

10.6038/cjg20150815.

10.6038/cjg20150815

P631

2014-01-20，2014-10-28收修定稿

王凌群， 李冰冰， 林君等. 2015. 航空电磁数据主成分滤波重构的噪声去除方法.地球物理学报，58(8):2803-2811,

Wang L Q, Li B B, Lin J, et al. 2015. Noise removal based on reconstruction of filtered principal components.ChineseJ.Geophys. (in Chinese),58(8):2803-2811,doi:10.6038/cjg20150815.