含流体孔隙介质中面波的传播特性及应用

张煜, 徐义贤, 夏江海, 张双喜, 平萍6,

1 武汉大学测绘学院, 武汉 430079 2 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079 3 武汉大学地球空间信息科学协同创新中心, 武汉 430079 4 中国地质大学(武汉)多尺度地球成像湖北省重点实验室, 武汉 430074 5 中国地质大学(武汉)地质过程与矿产资源国家重点实验室, 武汉 430074 6 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 武汉 430074



含流体孔隙介质中面波的传播特性及应用

张煜1,2,3,4, 徐义贤4,5, 夏江海4, 张双喜1,2,3, 平萍6,4

1 武汉大学测绘学院, 武汉 430079 2 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079 3 武汉大学地球空间信息科学协同创新中心, 武汉 430079 4 中国地质大学(武汉)多尺度地球成像湖北省重点实验室, 武汉 430074 5 中国地质大学(武汉)地质过程与矿产资源国家重点实验室, 武汉 430074 6 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 武汉 430074

基于单相介质中地震波理论的高频面波法已广泛应用于求取浅地表S波的速度.然而水文地质条件表明，普遍的浅地表地球介质富含孔隙.孔隙中充填的流体会显著地影响面波在浅地表的传播，进而造成频散和衰减的变化.本文研究了地震勘探频段内针对含流体孔隙介质边界条件的面波的传播特性.孔隙流体在自由表面存在完全疏通、完全闭合以及部分疏通的情况.孔隙单一流体饱和时，任何流体边界条件下存在R1模式波，与弹性介质中的Rayleigh波类似，相速度稍小于S波并在地震记录中显示强振幅.由于介质的内在衰减，R1在均匀半空间中也存在频散，相速度和衰减在不同流体边界下存在差异.Biot固流耦合系数(孔隙流体黏滞度与骨架渗透率之比)控制频散的特征频率，高耦合系数会在地震勘探频带内明显消除这种差异.介质的迂曲度等其他物性参数对不同流体边界下的R1波的影响也有不同的敏感度.完全闭合和部分疏通流体边界下存在R2模式波，相速度略低于慢P波.在多数条件下，如慢P波在时频响应中难以观察到.但是在耦合系数较低时会显现，一定条件下甚至会以非物理波形式接收R1波的辐射，显示强振幅.浅表风化层低速带存在，震源激发时的运动会显著影响面波的传播.对于接收点径向运动会造成面波的Doppler频移，横向运动会造成面波的时频畸变.孔隙存在多相流体时，中观尺度下不均匀斑块饱和能很好地解释体波在地震频带内的衰减.快P波受到斑块饱和显著影响，R1波与快P波有更明显关联，与完全饱和模型中不同，也更易于等效模型建立.频散特征频率受孔隙空间不同流体成分比例变化的控制，为面波方法探测浅地表流体分布与迁移提供可能性.通常情况孔隙介质频散特征频率较高，标准线性黏弹性固体可以在相对低频的地震勘探频带内等效表征孔隙介质中R1波的传播特征，特别在时域，可在面波成像反演建模中应用.

流体; 孔隙介质; 面波; 频散; 衰减

The pore fluid behaviors through the free surface make the boundary more complex as fully drained, fully sealed and partially drained conditions. These effects are taken into account in surface wave secular equation derivation and closed-form dynamic response investigation. Complex searching algorithm and fast coverage quadrature are applied in the dispersion and response calculation. Typical near surface earth media are selected. For weakly consolidated media in which the surface wave propagates in an extremely low velocity, the effects of the motion of source are obtained. The partial saturation of mesoscopic loss significant in seismic frequency band is introduced beyond the Biot model. The effective viscoelastic model that has been used for body waves in porous media is extended to solve the boundary value problem of surface wave propagation by coupling body wave representations on the free surface.

For one fluid saturated, R1 mode wave can propagate under each boundary condition, which is similar with classic Rayleigh wave in elastic media. Its phase velocity is a little less than the S wave and amplitude is strong in seismograms. Due to the intrinsic attenuation, R1 wave is dispersive in the homogeneous half space. The velocities and attenuation coefficients are different under different fluid boundary conditions. Biot solid-fluid coupling coefficient controls the critical frequency of dispersion as for the body waves. High solid-fluid coupling can eliminate the differences. Tortuosity affects R1 waves for different fluid boundaries with different sensitivities. R2 mode appears and propagates under sealed and partially drained conditions. Its phase velocity is a little less than P2 wave. In most cases, it is difficult to be observed in dynamic responses. However, when the solid-fluid coupling is low, it may obtain the radiation from R1 wave as a non-physical wave with strong amplitude under partially drained surface. When the velocity of surface wave is low in weak media, the movement of source impulse with regards to the receiver makes remarkable effects on surface wave responses. Radical velocity to the receiver makes Doppler frequency shift. Lateral velocity makes distortions of wave responses in time and frequency domains. For partial saturation with heterogeneous multiphase fluid saturated patches, the mesoscopic flow induced by wave can interpreter wave attenuation in seismic frequency band, which is accordance with the practical data. Because the fast P1 wave is dominantly affected by this strong loss mechanism, R1 wave is more distinctively related to P1 wave considering partial saturation, quite different to the Biot fluid saturated model. The critical frequency for mesoscopic mechanism is controlled by fluid compositions in the patches, which in turn presents the correlation for surface wave signals to subsurface fluid distribution and flowing. Because the Biot critical frequency is always high, standard linear viscoelastic solid can effectively represent R1 wave propagation in porous media in seismic frequency band by the coupling body wave fits and ignoring the slow wave perturbation, especially for the dynamic responses in the time domain. While in patchy saturation model, the P wave propagates under the interactive wave induced flow between the two P wave modes, which also make it simple to effectively represent.

The fluid phase in near surface media can be regarded as an important factor for surface wave data acquisition and processing. The effects of different fluid free surfaces need to be considered for correction in several unconsolidated and high permeability rocks. The low velocity of the surface wave makes the movement of source be an important impact in the frequency responses. For passive surface wave observation usually with low frequency signal extraction, this impact needs to be carefully estimated. The dominated mesoscopic mechanism in seismic frequency band shows obvious attenuation in the P wave, which also dominates the surface wave propagation. For near surface attenuation estimation by surface wave, the P wave must be paid attention to. The developed effective medium saves the storage and time consumption for surface wave in porous media, which can be applied in the inversion modeling for surface wave image in an economic way.Keywords Fluid; Porous media; Surface wave; Dispersion; Attenuation

1 引言

体波(P波和S波)在地表干涉产生沿自由表面传播的面波(Rayleigh波、Love波等).通过反演频散的面波速度，可获得不同尺度地下S波速度(Aki and Richards, 1980).面波方法已广泛地应用于水文、工程、环境、地质和地球物理等科学研究中.但该方法普遍基于弹性介质中面波的传播特性，经典线弹性理论是面波资料采集、处理和反演的理论基础(Song et al., 1989; Misiek et al., 1997; Xia et al., 1999, 2002, 2003, 2004, 2006a, 2006b, 2007, 2008, 2009; Winsborrow et al., 2003; Xu et al., 2006, 2007; Luo et al., 2007, 2008a, 2008b, 2009a, 2009b; Safani et al., 2006; Song et al., 2007; Zeng et al., 2007, 2011)

然而浅地表介质，通常都由富含孔隙的固体构成，孔隙中充填流体.这种介质的不均匀性会使波动传播显示出更复杂的特征.含流体孔隙介质理论较弹性理论更精确地揭示波动在真实介质中的传播规律.Biot提出的多相介质理论(Biot, 1941, 1856, 1962)将固体和流体耦合的宏观效应作为描述波动传播的物理机制.理论预言的慢P波随后被实验证实(Plona, 1980).该理论也成为研究孔隙介质中波动特征的基石.对于孔隙介质中的体波，近几十年已有较充分的论述(Carcione, 2007)，但是面波源于自由表面体波的干涉，传播特征更复杂，研究相对缺乏，限制了实际应用.故研究地震探测频带内孔隙介质中面波频散、衰减，以及动态响应特征是发展顾及含流体孔隙介质特征高精度面波方法的关键.

本文从几个方面回顾我们团队近几年在含流体孔隙介质中面波传播特征以及应用的研究，为进一步在实际面波探测中引入多相孔隙介质模型提供参考.

2 流体自由表面的边界效应

Deresiewicz和Skalak(1963)发现若自由表面存在流相，界面上孔隙疏通性的不同，存在“开放孔隙”，“闭合孔隙”，以及部分疏通多种边界条件.面波传播会受到多种流体自由表面边界效应的影响.基于Biot流体饱和模型的面波有零碎的研究.如Jones(1961)研究开放孔隙下孔隙介质半空间中Rayleigh面波，发现流体无黏性时仅存的一种无频散的面波.Deresiewicz(1962)进一步考虑流体黏滞性，面波发生频散，速度在一定频率下存在局部极小.Paul(1976a, 1976b)分析在自由表面稳态载荷的情况下包含面波的浅地表孔隙介质的位移响应.Tajuddin(1984)也基于无黏性流体，调查自由表面开放孔隙和闭合孔隙对面波传播的影响.Halpern和Christiano(1986)分析自由表面谐振下孔隙介质的动态响应.Philippacopoulos(1988)提出孔隙介质的Lamb问题，通过4个位移势函数获得开放孔隙下三维动态Green函数.Senjuntichai和Rajapakse(1994)研究相应的二维问题.国内学者王立忠等(1996)和杨峻等(1997)简化Biot模型，计算出稳态激振下的半空间孔隙介质的动态响应.夏唐代等(1998, 2004)提出忽略固流耦合的惯性效应的孔隙土力学模型，研究其中面波的频散和应力响应特征.刘凯欣和刘颖(2003)考虑孔隙介质各向异性对面波传播的影响.国内学者仅仅考虑开放孔隙条件.近年来也有学者发现闭合孔隙下，存在两种类型面波(Edelman and Wilmanski, 2002; Edelman, 2004; Albers and Wilmanski, 2005; Gerasik and Stastna, 2014).鉴于浅地表存在疏松土层、沥青路面，对应开放孔隙和闭合孔隙，以及两种极端情况之间更普遍的部分疏通条件，充分研究流体自由表面的边界效应对面波传播的影响很有必要.

除与弹性介质一样的固相应力边界条件(Carcione, 2007)，流体自由表面边界条件可写成(Deresiewicz and Skalak, 1963)

∂twz(x,y,z,t)|z=0-p(x,y,z,t)|z=0=0,

(1)

选取一组典型孔隙介质参数(见表1)，对应典型的含孔隙砂砾或礁石堆积物完全水饱和.其中λ和μ是骨架的拉梅常数，α和M是Biot参数，ρ和ρf分别是介质和流体的密度，η和k分别是流体的动态黏滞度和介质的宏观渗透率.

表1 孔隙介质模型参数Table 1 Model properties of a porous medium

图1 三种流体自由边界下表1孔隙介质中两类面波的相速度和衰减系数频散，速度和衰减都由干骨架中快P波——P1波参数归一化，参照的体波也绘制出(a) R1 波；(b) R2波.Fig.1 Phase velocities and attenuation coefficients of two surface wave modes in porous media corresponding to Table 1 under three fluid free surface boundaries. The velocity and attenuation is normalized by P1 wave in dry frame(a) R1 wave; (b) R2 wave.

2.1 固流耦合系数对流体自由表面边界效应的影响

固流耦合系数b控制孔隙介质的特征频率，随着流体的黏滞度或骨架的渗透率的变化而变化(b=η/k).图2所示R1波在其他参数不变，不同b时的特征.R1波频散随b的增大向高频移动.b较小时，骨架和流体的黏滞摩擦较小.因而体波的衰减会在更低频率下松弛，介质特征频率较低，反之亦然.这一特征也在面波中体现.R1波的衰减系数不随固流耦合系数的增大单调增加(图2右).这由于衰减系数f2和f1频率依赖的转化叠合特征频率增高的综合作用.非物理模式R1波随b增大在更高频出现.R2波随b增大，f1/2耗散频带扩大(图3).当b=9.6×104Pa·s/m2时，部分疏通下R2波在大于约65 Hz出现负衰减，也出现非物理波形式辐射(图3a右).其余条件下R2波的速度和衰减只比闭合孔隙时略小(图3b—3d).与R1波不同的是，R2波随b增大，速度单调降低，衰减系数单调升高.

进一步计算在垂直于自由表面应力源下面波的地震动响应，集中力点震源方程为

τzz(x,y,z,t)|z=0=-F(t)δ(x)δ(y),

(2)

τzz为孔隙介质垂向正应力.震源作用幅度为1N，时间函数F(t)为Ricker子波，主频和时移分别是35 Hz和0.1 s.图4所示表1介质参数，375 m偏移距下，图2—3中对应5种b时面波垂直位移地震动响应.R1波振幅和相位的差异表明其受流体自由边界效应的影响，而快P波——P1波则差异很小.但是随b增大，R1波的差异性减弱.振幅和相位的特征也反映相速度和衰减系数在震源子波频带内的特性.R2波在多数情况下不可见，因为震源频带大部分落入f1/2强耗散区.只有当b=9.6×104Pa·s/m2时，R2波出现.需注意的是，部分疏通时R2波振幅甚至大于R1波.这时R2波衰减系数更小，大于65 Hz甚至出现负衰减(图3a右).可能存在R1波向R2波的辐射，这也可解释闭合孔隙和部分疏通的R1波衰减系数相近(图2a)，但部分疏通时的R1波振幅更弱(Zhang et al., 2011).

2.2 孔隙迂曲度对流体自由表面边界效应的影响

Berryman(1980)给出由孔隙度估计孔隙迂曲度的公式，

C=1-r0(1-1/φ),

(3)

其中r0为固体颗粒形状参数，r0=1/2代表球状颗粒，其他椭球体r0取值0～1.近似地，一般我们取球状颗粒时的迂曲度.圆柱状孔隙且平行于流体压力梯度，C=1，为迂曲度最小值，随机孔隙分布，C=3(Mavko et al., 1998).图5所示R1波在迂曲度为1、2、3时频散的相速度和衰减系数.C较小时R1波频散更明显.这由于流体流动受迂曲度的影响，迂曲度较小时，流体流动受阻碍更小，固流相互作用更大，衰减得以显现.C变化时，开放孔隙时R1波的速度和衰减变化幅度最小，对流体流动变化最不敏感.图6所示R2波在迂曲度为1、2、3时频散的相速度和衰减系数.两种情况下R2波有相似特征，C较大时频散的幅度会减小，类似R1波.随C变大，部分疏通下R2波与闭合孔隙下R2波的衰减系数的分离出现在更低频率，差异也更明显.

图7所示与图4相同震源和接收参数时，迂曲度为1、2、3时面波地震动响应特征.孔隙迂曲度较小时，R1波振幅最弱，随着C的增加，R1波振幅增强.参照P1波，迂曲度变化时，三种流体边界下波形和振幅差异较小，说明P1波受孔隙流体的影响较R1波小.R2波没有观察到.

3 移动震源激发效应

由于浅地表岩石的固结程度低，某些软弱土层中面波速度很低.这时，震源激发的速度会对面波地震动响应造成明显的影响.含流体孔隙介质在移动震源激发下的动态响应是重要的工程问题，如Burke和Kingsbury(1984)给出在地表移动压力下孔隙介质响应的解析解.Siddharthan等(1993)忽略固流耦合，分析平面应变下移动载荷下多层孔隙介质响应.Jin等(2004)获得地表匀速线载荷下的二维介质响应的半解析表达.Theodorakopoulos(2003), Theodorakopoulos等(2004)通过移动线载荷的解析和近似数值方法研究二维土壤介质的响应.Lu和Jeng(2007)首次推导匀速点载荷下的三维孔隙介质的动态响应.Xu等(2008)进一步扩展到多层的情况.Cai等(2007, 2008)研究有限矩形载荷和轨道系统下，骨架不可压缩时三维稳态响应.Cao和Boström (2013)研究加速和减速的火车载荷轨道系统激发的孔隙介质响应特征.Lefeuve-Mesgouez和Mesgouez (2008, 2012)通过波模态分析半空间及多层孔隙黏弹性介质在高速谐振矩形载荷下的地震动传播过程.Li等(2012)分析孔隙介质的波数域近似解表示移动谐振下半空间响应的精度.Beskou和Theodorakopoulos(2011)全面回顾移动激发问题.稳态载荷(单色频率)过于简单，不能有效利用振动响应包含面波传播的有效信号.将移动载荷视为有限频率噪声源，并考虑流体自由表面边界效应，分析激发的面波传播特征可以更充分认识移动震源效应的影响.

图2 不同固流耦合系数时R1波的相速度和衰减系数频散Fig.2 Phase velocity and attenuation coefficient of R1 wave for different solid-fluid coupling coefficients

图3 不同固流耦合系数时R2波的相速度和衰减系数频散Fig.3 Phase velocity and attenuation coefficient of R2 wave for different solid-fluid coupling coefficients

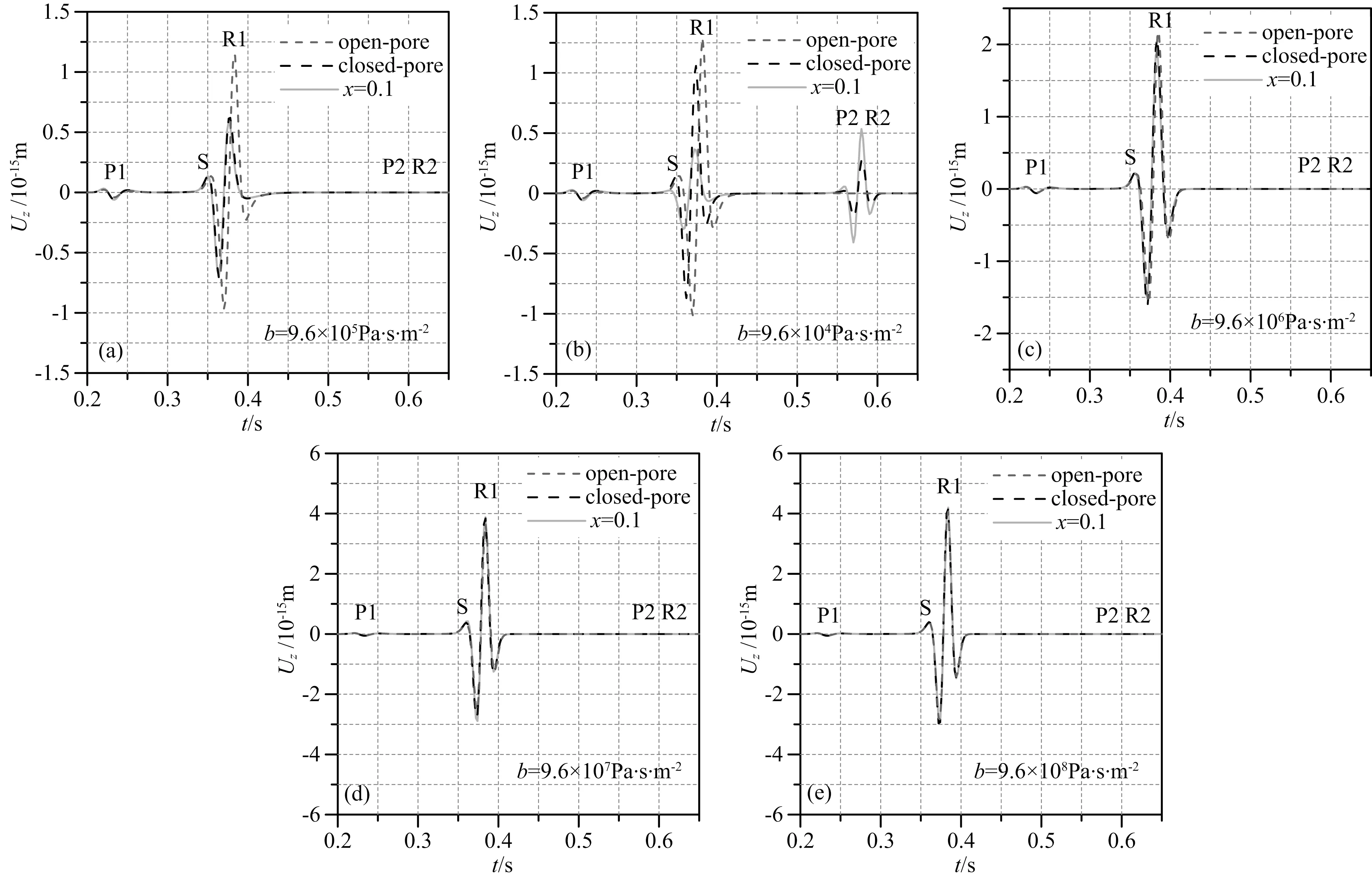
图4 不同固流耦合系数时面波的地震动响应Fig.4 Seismic responses of surface wave for different solid-fluid coupling coefficients

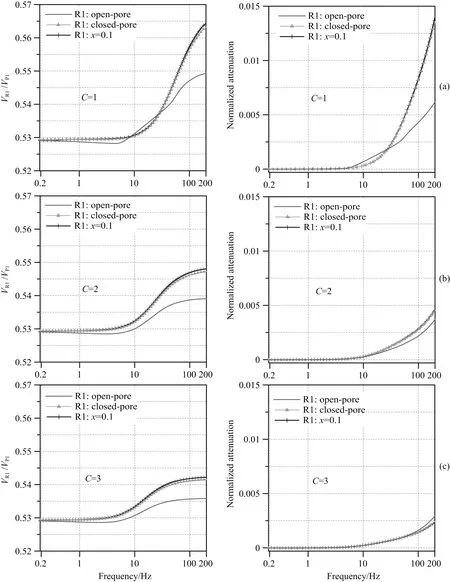
图5 不同孔隙迂曲度时R1波的相速度和衰减系数频散Fig.5 Phase velocity and attenuation coefficient of R1 wave for different tortuosities

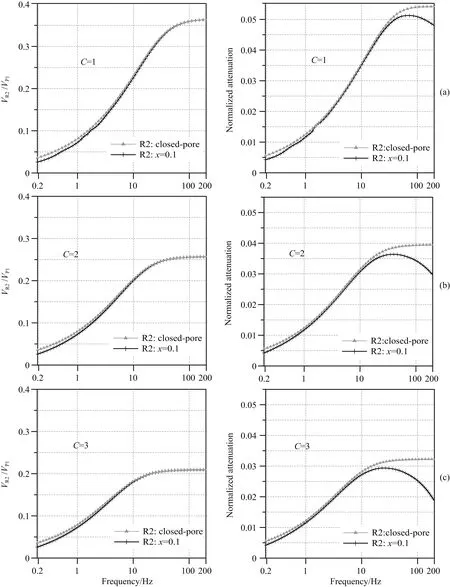
图6 不同孔隙迂曲度时R2波的相速度和衰减系数频散Fig.6 Phase velocity and attenuation coefficient of R2 wave for different tortuosities

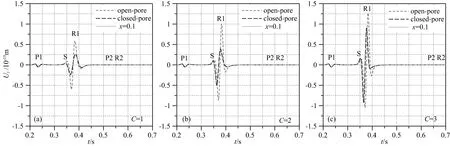
图7 不同孔隙迂曲度下面波的地震动响应Fig.7 Seismic responses of surface wave for different tortuosities

图8 xy平面内以匀速v沿x运动的移动震源和接收点的相对位置Fig.8 The decomposition of the velocity of the moving impulse along x axis related to the receiver on the xy plane

软弱孔隙介质参数见表2，对应某一高速公路施工现场采集的未固结砂岩样本.该样本有较低的剪切模量和较高的渗透率，反映浅表含水层的典型地质条件.流体对应浅地表水的状况.选择沿x轴方向以速度v移动的地表点应力震源，可以写成

τzz(x,y,z,t)|z=0=-F(t)δ(x-vt)δ(y).

(4)

对比方程(3)，加入震源速度的扰动，作坐标参数替换x′=x-vt.震源幅度为100N，震源过坐标原点时开始计时，时间响应仍为Ricker子波，时移0.05s，接收点在(30m, 30m, 1m)处(图8).选择低主频5Hz震源突出震源移动的影响(Zhangetal., 2014a).图9所示三种流体自由表面(开放孔隙、闭合孔隙以及渗透刚度0.1时部分疏通情况)下垂直位移和孔隙流体压力的面波地震动响应.表2对应等效Gassmann介质Rayleigh波速度约为169m·s-1，移动震源速度选择从亚Rayleigh波速度(40m·s-1)到超Rayleigh波速度(200m·s-1).只有P1和R1波可以分辨.震源速度增大到169m·s-1，所有波形明显压缩.震源速度进一步增大到200m·s-1，这些现象更为明显.这源于Doppler蓝移，由径向视速度产生(图8).图10比较开放孔隙时垂直位移和流体压力在震源速度v为40 m·s-1和200 m·s-1时功率谱.相比v=40 m·s-1，v=200 m·s-1时频率成分有明显的上移，无论垂直位移还是流体压力，主频甚至大于10 Hz，比震源原始主频5 Hz大1倍.移动震源的Doppler效应对面波传播频率响应有明显影响.波形扭曲出现，特别是R1波，表现为子波拖长.这源于横向速度(图8).主频较低(5 Hz)，子波时长大概0.2 s(T≈1/5=0.2 s)，移动震源激发时有明显的横向移动.

4 多相流体效应

孔隙中流体的特性会极大地影响介质中波动传

表2 软弱孔隙介质物性参数Table 2 Model properties of a weakly porous medium

播.通常情况，孔隙空间内通常是气体和液体混合充填的，这时在地震频带内Biot宏观固流耦合效应难以解释观测到的衰减.有研究表明(Pride et al., 2004)，中观尺度的流体斑块饱和是造成波动衰减的主要因素.这种机制由于中观尺度下波动激发的流体流动造成.White(1975)最早建立分离的球状气体饱和斑块和液体饱和背景模型来描述这一特征.波动造成的流体压力梯度使气饱和斑块扩散形变，驱动斑块和背景间的流体对流，导致介质的本征衰减(Johnson, 2001; Vogelaar et al., 2010).这一低频的部分饱和效应已在体波研究中得到广泛重视.观测资料和数值模拟也与这种斑块饱和模型一致(Wenzlau and Müller, 2009)，波动激发的对流改变介质整体的频率响应(Saenger et al., 2009).面波由体波干涉而成，斑块饱和这一机制必然会影响面波.进一步理解斑块饱和对面波的影响可以使我们更精确估计面波波速和衰减，建立更精确反演成像模型.

中观尺度(典型值为数十厘米)远大于孔隙尺度，又远小于波长.因此，在中观尺度上，波动激发的流体压力变化在一个波动周期内不能完全平衡.非均匀的斑块饱和经常产生于气液接触区域.在完全气饱和及完全液饱和区域之间，通常会有一转换区域存在.波动激发的对流会在这一区域内造成压力梯度，并驱使气流接触面的扩散效应(Pride and Berryman, 2003).

(5)

整个介质在低频极限下或称之静态极限下的等效体积模量，可以写成

KGW=Km+α2M(Kw),

(6)

其中Km是骨架的体积模量，KGW是等效流体孔隙介质的Gassmann体积模量.

频率足够高，波周期内流体不能完全松弛，造成流体的压力梯度.区域内的流体压力不一致，但仍可假设各个流相中的压力一定.介质的体积模量可以通过Hill理论给出.

(7)

或者Voigt等效流体的Gassmann体积模量给出

KGV=Km+α2M(KV),

(8)

其中

KV=∑SiKfi,

(9)

忽略对流效应，也称之为非流动极限(Mavkoetal., 1998).

在两极限频率之间的转换反映斑块饱和模型中波动的频率响应，体现中观机制的影响.White(1975)的处理方法(Dutta和Seriff(1979)修正)获取这一模型复频率效应.Johnson(2001)推广White模型得到因果性的近似广义解.Vogelaar等(2010)进一步给出精确解.

斑块饱和介质性质如表3所示.同心球壳的外半径为b=20 cm，代表斑块的尺度.整个斑块饱和介质源自XH高速公路附近采集的空气-水饱和未固结含砂粘土样本.

图12a显示多相流体斑块饱和介质中频散的P1波相速度和衰减(1/Q).其中气体占流体比例为0.3.在低频端P1波接近静态极限；在高频端P1波接近非流动极限.两极限之间的转换在地震频带内显现(1～200 Hz)，这也解释了这一频带内波动传播的主要衰减.可以发现方程fm=Kf2k/2πη2φ(b-a)2(图中垂直点线)给出近似的转换特征频率 (DuttaandSerriff, 1979)，这一频率也区分松弛和非松弛状态.但需要注意，这一机制在Biot理论框架内对S波影响较小，因为两种极限对于S波来说相互重合.这一结论，亦被数值模拟验证(Rubinoetal., 2009;Liuetal., 2009a).

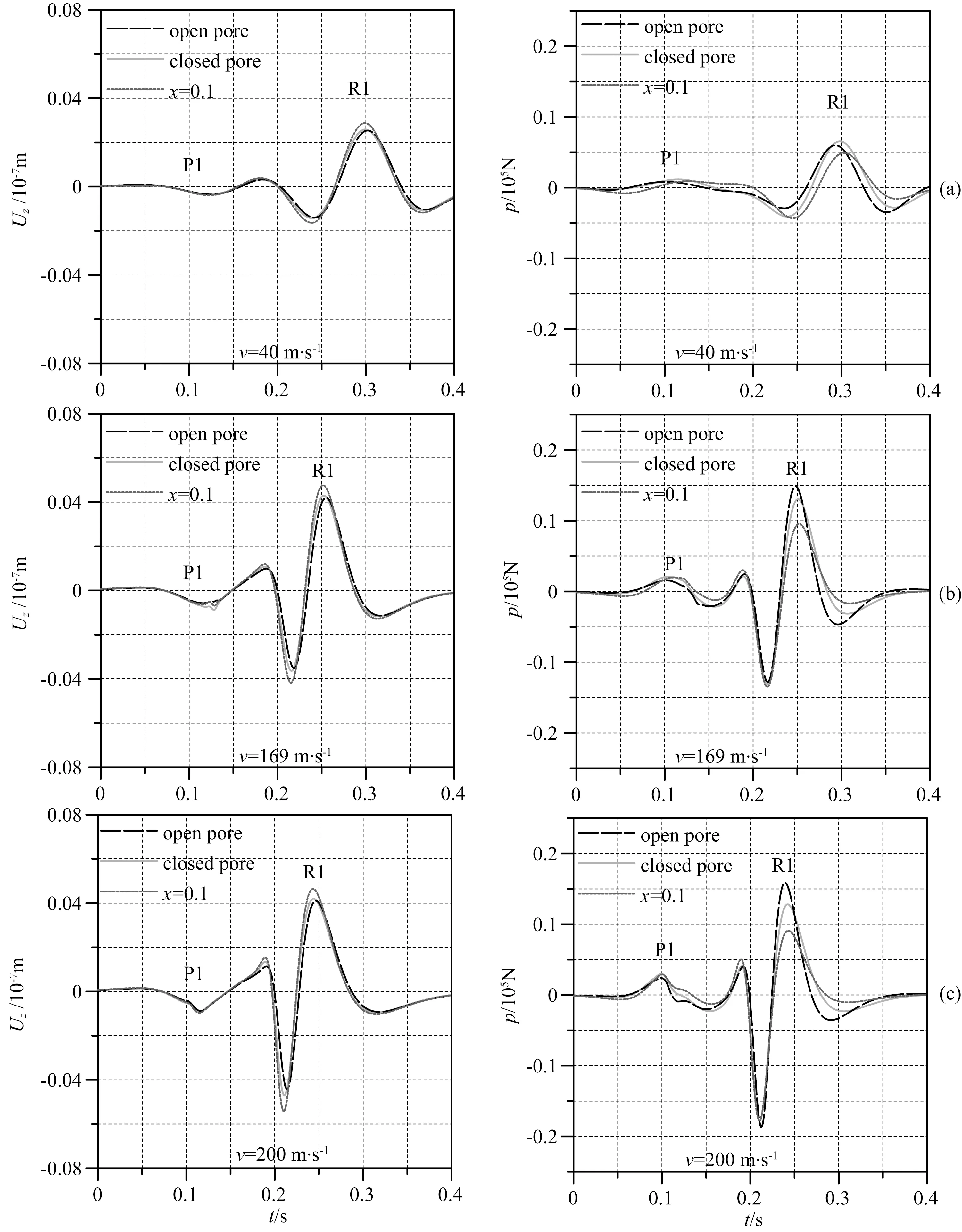
图9 不同震源移动速度下固体垂直位移和孔隙流体压力的面波地震动响应Fig.9 Seismic responses of solid vertical displacement and pore fluid pressure for different source velocities

图10 震源移动速度为40 m·s-1和200 m·s-1时固体垂直位移(a)和孔隙流体压力(b)面波地震动的功率谱Fig.10 Power spectra of solid vertical displacement (a) and pore fluid pressure (b) of surface wave seismic responses for source velocities at 40 m·s-1 and 200 m·s-1

图11 由周期性的半径为a，相隔距离为2b′的球状气体饱和区域构成的立方体格子，改自Vogelaar et al., 2010每一气体饱和区域由一个外半径为b的液体饱和的球壳包围， 所以立方体格子的体积等于同心球体的体积，即Vb′= Vb.Fig.11 Geometry of the cubic lattice of periodic spherical gas pocket with radius a, separated by distance 2b′ (from Vogelaar et al., 2010)Each gas pocket is surrounded by a liquid shell with radius b, so that the volume of the cube equals to the volume of the sphere Vb′=Vb.

宏观上描述该模型的自由表面边界效应，可以用等效复体积模量表征的边界条件来获取Rayleigh面波的久基方程和地震动动态响应(Zhangetal., 2014b).选择和体波分析一致的介质模型，面波频散的相速度和衰减如图12b所示.斑块饱和衰减同样在低频段的面波频散中显现，与P1波类似(图12a).转换也在两个频率极限——静态极限和非流动极限之间出现(图12b左).衰减1/Q较水饱和和气饱和下明显增强.对应最大1/Q转换特征频率在数十赫兹内显现，落入地震频带内，也与P1波类似(图12a右).因为S波受流体分布影响较小，面波的这一趋势主要反映P1的影响.虽然面波相对P1波的敏感性不如S波显著(Xia et al., 1999)，但低频段内P1波的影响不能被忽略.Biot机制特征频率很高，可以推断在低频带内，斑块饱和衰减机制对面波的衰减有显著的影响.因而必须小心建立面波的衰减模型，同时强调频率依赖和P1波的影响.

面波的地震动响应也反映这一特征(图13)，其中震源为Ricker子波，主频35 Hz，时移0.1 s，幅度100 N，偏移距200 m.可以看到顾及斑块饱和机制的面波如P1波一样，比水饱和气饱和仅有Biot宏观机制时振幅明显衰减.

数值实验还发现，这一中观尺度上的面波衰减与气体在流体中的比例有很明显的关系，也为利用面波探测地下流体分布提供可能(Zhang et al., 2014b).

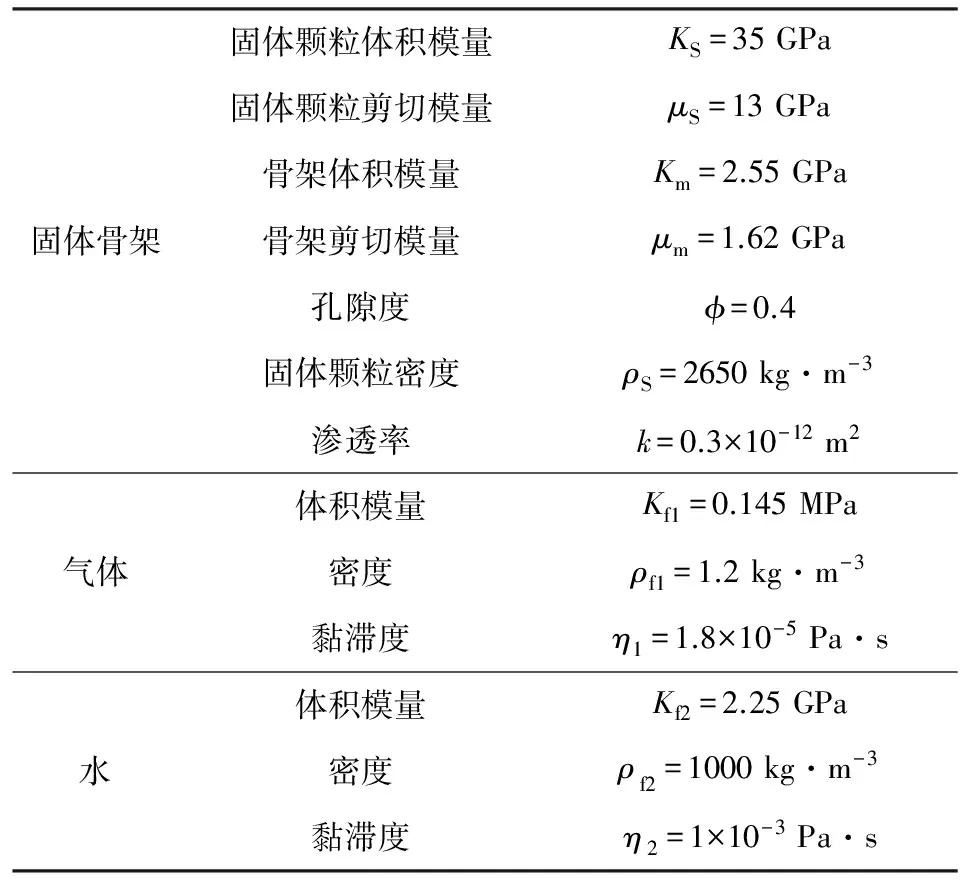
表3 斑块饱和孔隙介质的物性参数Table 3 Model properties of a patchy saturated porous medium

5 面波传播的等效特征

P2波在低频段速度低，且具有很强的扩散性质，造成Biot波动方程数值计算时很不稳定，需要很大的存储量和计算时间(Carcione and Quiroga-Goode, 1995, 1996).为克服这些困难，找到孔隙介质中波动传播的等效解是有效手段.应用黏弹性等效单元模拟宏观固流耦合效应研究体波传播最早见于Geertsma和Smit(1961)的研究.P1波的品质因子(Q)满足Q>5，孔隙介质中的衰减可用一单元的标准线性体(Zener体)等效表示(Ben-Menahem and Singh, 1981).Carcione(1998)成功地应用Zener等效固体表征Biot宏观流和喷流机制(Dvorkin et al., 1994).并成功模拟包含P波和S波的等效波场，建立记忆变量等效代替.虽然Biot的宏观流机制不涉及固体的体形变，但是用Zener模型，可直接匹配每一种波型的频散和衰减(Carcione, 1998).这种等效模型也用来描述波动散射的问题(Morochnik and Bardet, 1996).最近的研究表明，这种等效模型也可以用来表述部分饱和(Rubino et al., 2009; Picotti et al., 2010, 2012a; Carcione et al., 2012)、双孔隙(Liu et al., 2009b, 2010)，以及多相固体等提升Biot模型(Picotti et al., 2012b).这些研究表明，复杂介质可用简单的等效介质表征，等效黏弹性固体中用松弛函数直接匹配每一种波型可以有效地表征孔隙介质中波动传播的宏观特征(Carcione, 2007).由于自由表面的存在，Rayleigh面波的数值计算方法面临更为严苛的不稳定问题，即便是在完全弹性固体中，需要在很小的网格中求解差分方程(Xu et al., 2007; Zeng et al., 2011).流体自由表面会使面波特征更为复杂(Zhang et al., 2011, 2012)，数值计算的稳定性更差.这也为实际面波应用中引入多相孔隙模型带来困难.因此，在前人用等效固体表征体波的同时，我们也需要回答包含自由界面效应的面波是否也可用等效黏弹性固体表征.

图12 P1波(a)和R1波(b)在斑块饱和模型中的相速度和衰减频散特征.S1=0.3，b=0.2 m上下水平线表示两极限频率下的体积模量KGW和KGH.垂直的点线近似表示转换特征频率.R1波衰减的对照组代表气饱和和水饱和时的情况.Fig.12 Phase velocities and attenuation of P1 wave (a) and R1 wave (b) in the patchy saturation model. S1=0.3, b=0.2 m The lower and upper horizontal lines are obtained from limiting modulus KGW and KGH. The vertical dot line is the approximating transition frequency. The control groups for R1 attenuation represent the half space fully saturated by air and water.

图13 面波在斑块饱和模型中的地震动响应.S 1=0.3，b=0.2 m 对照组代表气饱和水饱和时的情况.Fig.13 Seismic responses of surface wave in the patchy saturation model. S1 = 0.3 and b=0.2 mThe control groups represent the half space fully saturated by air and water.

基于含流体孔隙介质模型，等效黏弹性模型可由黏弹性单元替代原本构方程中的复模量实现(Carcione, 2007).在单相的黏弹性模型中，体波可以等效地用速度和衰减相关的松弛模式等效表征.Rayleigh面波也可以用包含两种体波松弛模式的黏弹性固体结合边界条件实现.

使用标准线性体模型(Zener模型)来表征快波(P1波和S波)，Zener黏弹性单元的复模量可以表示成(Carcione, 2007)

(10)

其中M0是介质松弛模量，τε和τσ分别是应力和应变松弛时间.每一种体波，只需一种黏弹性单元就足以表征体波在孔隙介质中的行为.因此，每一体波只需要一组松弛时间τε和τσ来表征.在Zener模型中，松弛时间可表示成

(11)

其中ω0=2πf0对应波动衰减峰值频率，Q0是该频率f0下的品质因子.在等效介质中，孔隙流体的自由表面效应被忽略，整个介质的衰减由黏弹性固体的松弛机制代替.等效的表征可以简单替换(11)中的对应快波的模量，松弛时间以相应P1波和S波的f0i和Q0i,i=P,S求得，同时忽略P2波的影响.等效波动方程可通过Biot方程中对应等效替换并去掉P2波项得到(Zhang et al., 2014c).

面波的等效相速度和1/Q亦可通过求解等效介质中Rayleigh面波的久基方程求得，相应的面波地震动响应可以通过类似的积分变换方法得到.

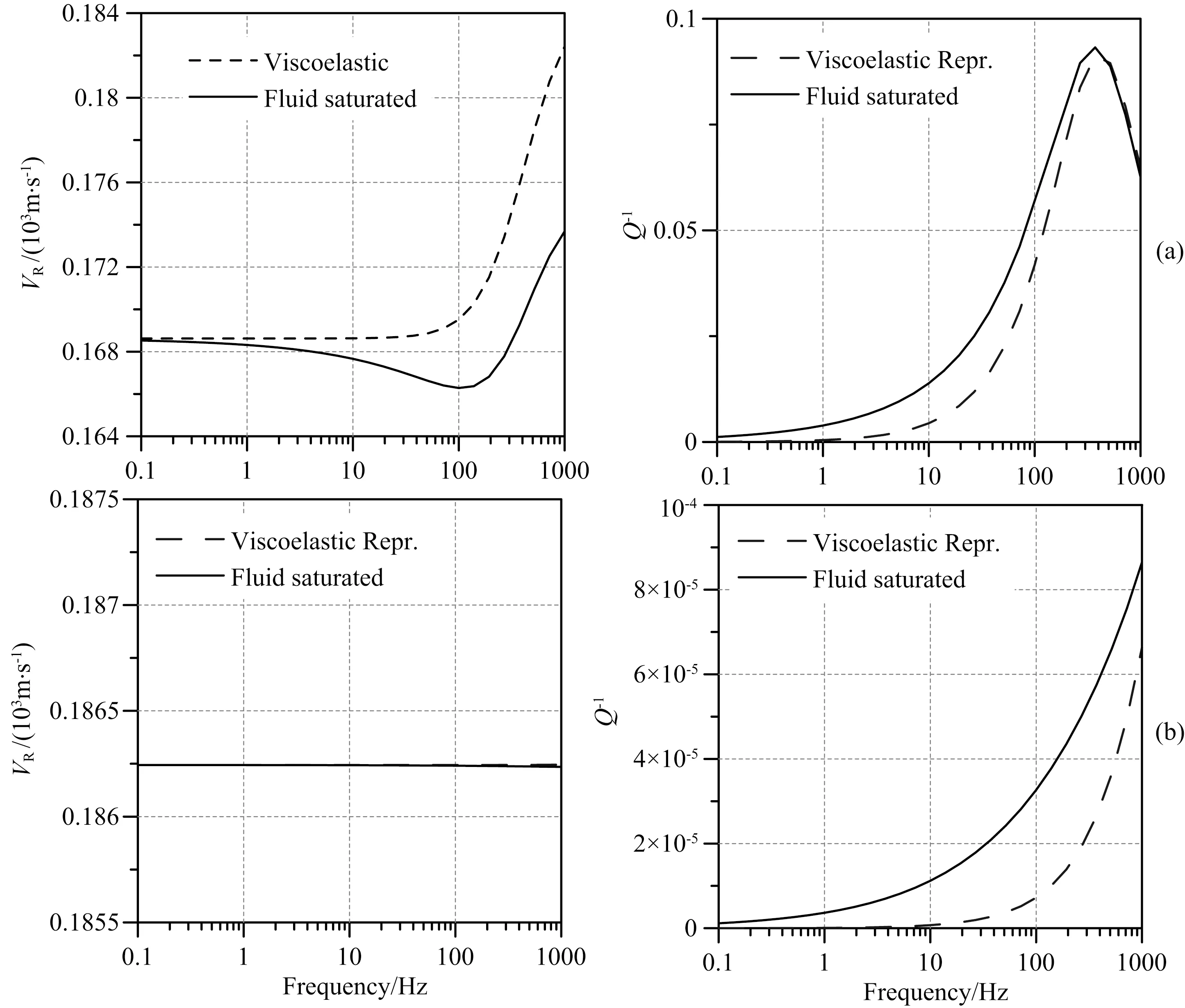
图14 面波在未固结砂岩中相速度(左)和衰减(右)的频散孔隙中充填水(a)和空气(b).两种等效黏弹性固体中快波的衰减峰值频率和品质因子分别为436.9 Hz, 421.0 Hz 和 17.5, 13.3 (a)，以及12488.5 Hz, 5840.9 Hz和4488.5, 9200.6 (b).孔隙含水的情况下，等效介质在低频段低估面波的衰减.Fig.14 The dispersion of phase velocity (left) and attenuation (right) of surface wave in the unconsolidated sand for water (a) and air (b) saturated models The two equivalent-viscoelastic materials have relaxation frequency of 436.9 Hz, 421.0 Hz and quality factor of 17.5, 13.3 for the two body wave modulus for the water case (a), and relaxation frequency of 12488.5 Hz, 5840.9 Hz and quality factor of 4488.5, 9200.6 for the air case (b), respectively. The effective representation underestimated the attenuation for the water case at low frequencies.

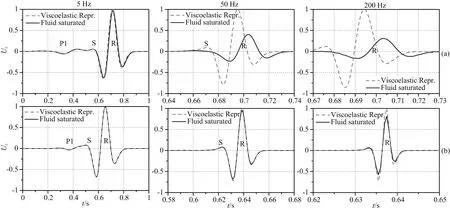
图15 面波在未固结砂岩中的等效地震动响应波形孔隙中充填水(a)和空气(b).震源激发的主频分别为5 Hz(左)、50 Hz(中)和200 Hz(右).除50 Hz和200 Hz孔隙含水时(a)，等效介质中波形显示出与孔隙介质相当好的一致性.Fig.15 Seismic responses of surface wave in the unconsolidated sand for water (a) and air (b) saturated models The source pulses have center frequency of 5 Hz (left), 50 Hz (center), and 200 Hz (right). Except for 50 Hz and 200 Hz for water case (a), the wave forms show a fairly well match with the fluid-saturated model.

图15所示未固结砂岩中面波的垂直位移地震动响应.接收点位于自由表面，偏移距为100 m.时移0.1 s的Ricker子波震源的主频fs分别为5 Hz(左)、50 Hz(中)和200 Hz(右).在孔隙含水时(图15a)，震源主频为50 Hz和200 Hz时，等效黏弹性介质未能拟合孔隙介质中的波形.而在fs=5 Hz则显示出相当好的拟合效果.而在孔隙含空气时(图15b)，所有结果都显示出较好的一致性.

含多相流体的孔隙介质，由于P1、P2波的共同作用造成中观尺度下对流，引起波传播的衰减，也可以直接对等效体积模量以及S波做黏弹性等效替换，得到类似的等效表征模型(Zhang et al., 2014d).

6 结论及展望

精确认识面波在真实介质传播时的速度和衰减特征是提高面波方法勘探精度的基础.本文从面波的几个方面详细讨论了面波在更接近实际介质的孔隙介质模型中的传播特性，获得以下几点认识：

(1)流体在自由表面不同行为造成面波传播的差异使得在面波的数据采集和处理时，根据不同地表条件引入流体自由表面效应的修正.特别是针对浅地表岩石固结程度低、渗透率较高的情况.有些特殊情况甚至要考虑第二模式面波的影响.这种修正的方法和评价标准，需要再结合实际情况进一步的研究.

(2)针对浅地表介质软弱，面波速度较低的情况，震源激发时移动速度有时候也需要评价.相对于观测点的径向、横向移动会造成面波信号频率响应的明显变化，特别是震源激发频率较低时.在有着较高速度移动噪声源的环境中，这种效应的影响需要根据采集观测系统和主要噪声源的方位判断.扰动的影响的大小需要根据实际采集环境谨慎地评价.

(3)当介质部分饱和时，中观尺度多相流体的斑块饱和效应会在地震探测频带内显著影响面波的传播.这一机制主要影响胀缩运动的P波，故而在地震频带内估计面波的衰减，需要重新重视P波的影响.

(4)根据面波的传播特征建立等效黏弹性模型，在地震探测频带内能较好地表征面波在孔隙介质中的传播，这有利于在面波的数值计算中更经济地引入孔隙介质模型，建立更少参数约束的面波反演成像模型.

可以发现，含流体的孔隙介质中面波的传播较弹性介质更为复杂.在面波实际应用中顾及复杂传播特性影响的研究尚在起步阶段，如何更合理有效地引入孔隙介质模型，有更多的理论实际问题需要进一步探讨.

致谢 感谢匿名审稿人对本文的建议.

Aki K, Richards P G. 1980. Quantitative Seismology. San Francisco: Freeman. Albers B, Wilmanski K. 2005. Monochromatic surface waves on impermeable boundaries in two-component poroelastic media.ContinuumMechanicsandThermodynamics, 17(3): 269-285,

Ben-Menahem A, Singh S G. 1981. Seismic Waves and Sources. New York: Springer-Verlag.

Berryman J G. 1980. Confirmation of Biot′s theory.Appl.Phys.Lett., 37(4): 382-384, doi: 10.1063/1.91951.

Beskou N D, Theodorakopoulos D D. 2011. Dynamic effects of moving loads on road pavements: A review.SoilDyn.Earthq.Eng., 31(4): 547-567, doi: 10.1016/j. soildyn.2010.11.002.Biot M A. 1941. General theory of three-dimensional consolidation.J.Appl.Phys., 12(2): 155-164, doi: 10.1063/1.1712886.

Biot M A. 1956. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range.J.Acoust.Soc.Am., 28(2): 168-178, doi: 10.1121/1.1908239.

Biot M A. 1962. Mechanics of deformation and acoustic propagation in porous media.J.Appl.Phys., 33(4): 1482-1498, doi: 10.1063/1.1728759.

Burke M, Kingsbury H B. 1984. Response of poroelastic layers to moving loads.Int.J.SolidsStruct., 20(5): 499-511, doi: 10.1016/0020-7683(84)90015-5.

Cai Y Q, Sun H L, Xu C J. 2007. Steady state responses of poroelastic half-space soil medium to a moving rectangular load.Int.J.SolidsStruct., 44(22-23): 7183-7196, doi: 10.1016/j.ijsolstr.2007.04.006.

Cai Y Q, Sun H L, Xu C J. 2008. Response of railway track system on poroelastic half-space soil medium subjected to a moving train load.Int.J.SolidsStruct., 45(18-19): 5015-5034, doi: 10.1016/j.ijsolstr.2008.05.002.

Cao Z G, Boström A. 2013. Dynamic response of a poroelastic half-space to accelerating or decelerating trains.J.SoundVib., 332(11): 2777-2794, doi: 10.1016/j.jsv.2012.12.015.

Carcione J. 2007. Wave Fields in Real Media: Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnetic Media. 2nd ed. Amsterdam: Elsevier.

Carcione J M, Quiroga-Goode G. 1995. Some aspects of the physics and numerical modeling of Biot compressional waves.J.Comput.Acoust., 3(4): 261-280, doi: 10.1142/S0218396X95000136.Carcione J M, Quiroga-Goode G. 1996. Full frequency-range transient solution for compressional waves in a fluid-saturated viscoacoustic porous medium.Geophys.Prospect., 44: 99-129, doi: 10.1111/j.1365-2478.1996.tb00141.x.

Carcione J M. 1998. Viscoelastic effective rheologies for modelling wave propagation in porous media.Geophys.Prospect., 46(3): 249-270, doi: 10.1046/j.1365-2478.1998.00087.x.

Carcione J M, Gei D, Picotti S, et al. 2012. Cross-hole electromagnetic and seismic modeling for CO2detection and monitoring in a saline aquifer.J.Petrol.Sci.Eng., 100: 162-172, doi: 10.1016/j.petrol.2012.03.018.

Deresiewicz H. 1962. The effect of boundaries on wave propagation in a liquid-filled porous solid. IV. Surface waves in a half-space.Bull.Seismol.Soc.Am., 52(3): 627-638.

Deresiewicz H, Skalak R. 1963. On uniqueness in dynamic poroelasticity.Bull.Seismol.Soc.Am., 53(4): 783-788.

Dutta N C, Seriff A J. 1979. On White′s model of attenuation in rocks with partial gas saturation.Geophysics, 44(11): 1806-1812, doi: 10.1190/1.1440940.

Dvorkin J, Nolen-Hoeksema R, Nur A. 1994. The squirt-flow mechanism: macroscopic description.Geophysics, 59(3): 428-438, doi: 10.1190/1.1443605.

Edelman I, Wilmanski K. 2002. Asymptotic analysis of surface waves at vacuum/porous medium and liquid/porous medium interfaces.ContinuumMechanicsandThermodynamics, 14(1): 25-44, doi: 10.1007/s001610100069.

Edelman I. 2004. Surface waves at vacuum/porous medium interface: low frequency range.WaveMotion, 39(2): 111-127, doi: 10.1016/j.wavemoti.2003.07.004.

Geertsma J, Smit D C. 1961. Some aspects of elastic wave propagation in fluid-saturated porous solids.Geophysics, 26(2): 169-181, doi: 10.1190/1.1438855.

Gerasik V, Stastna M. 2014. Pseudo-interface Rayleigh wave on a permeable porous medium/vacuum interface.J.Acoust.Soc.Am., 135(5): 2625-2633, doi: 10.1121/1.4869692.

Halpern M R, Christiano P. 1986. Response of poroelastic halfspace to steady-state harmonic surface tractions.Int.J.Nemer.Anal.Meth.Geomech., 10(6): 609-632, doi: 10.1098/rspa.2007.0107.

Jin B, Yue Z Q, Tham L G. 2004. Stresses and excess pore pressure induced in saturated poroelastic halfspace by moving line load.SoilDyn.Earthq.Eng., 24(1): 25-33, doi: 10.1016/j.soildyn.2003.09.004.

Johnson D L. 2001. Theory of frequency dependent acoustics in patchy-saturated porous media.J.Acoust.Soc.Am., 110(2): 682-694, doi: 10.1121/1.1381021.Jones J P. 1961. Rayleigh wave in a porous elastic saturated solid.J.Acoust.Soc.Am., 33(7): 959-962, doi: 10.1121/1.1908865.Lefeuve-Mesgouez G, Mesgouez A. 2008. Ground vibration due to a high-speed moving harmonic rectangular load on a poroviscoelastic half-space.Int.J.SolidsStruct., 45(11-12): 3353-3374, doi: 10.1016/j.ijsolstr.2008.01.026. Lefeuve-Mesgouez G, Mesgouez A. 2012. Three-dimensional dynamic response of a porous multilayered ground under moving loads of various distributions.Adv.Eng.Software, 46(1): 75-84, doi: 10.1016/j.advengsoft.2010.09.006.

Li S, Sun H L, Cai Y Q, et al. 2012. Validity of fully drained, fully undrained andu-pformulations for modeling a poroelastic half-space under a moving harmonic point load.SoilDyn.Earthq.Eng., 42: 292-301, doi: 10.1016/j. soildyn.2012.06. 016.

Liu K, Liu Y. 2003. Characteristic of Rayleigh waves in transversely isotropic fluid-saturated porous media.ActaMechanicaSinica(in Chinese), 35(1): 100-104.

Liu X, Greenhalgh S, Zhou B. 2009a. Scattering of plane transverse waves by spherical inclusions in a poroelastic medium.Geophys.J.Int., 176(3): 938-950, doi: 10.1111/j.1365-246X.2008.04026.x.

Liu X, Greenhalgh S, Zhou B. 2009b. Transient solution for poro-viscoacoustic wave propagation in double porosity media and its limitations.Geophys.J.Int., 178(1): 375-393.

Liu X, Greenhalgh S, Zhou B. 2010. Approximating the wave moduli of double porosity media at low frequencies by a single Zener or Kelvin-Voigt element.Geophys.J.Int., 181(1): 391-398, doi: 10.1111/j.1365-246X. 2009.04144.x.

Lu J F, Jeng D S. 2007. A half-space saturated poro-elastic medium subjected to a moving point load.Int.J.SolidsStruct., 44(2): 573-586, doi: 10.1016/j.ijsolstr.2006.05.020.

Luo Y H, Xia J H, Liu J P, et al. 2007. Joint inversion of high-frequency surface waves with fundamental and higher modes.J.Appl.Geophys., 62(4): 375-384, doi: 10.1016/j.jappgeo.2007.02.004.

Luo Y H, Xia J H, Miller R D, et al. 2008a. Rayleigh-wave dispersive energy imaging using a high-resolution linear Radon transform.PureAppl.Geophys., 165(5): 903-922, doi: 10.1007/s00024-008-0338-4.

Luo Y H, Xia J H, Liu J P, et al. 2008b. Generation of a pseudo-2D shear-wave velocity section by inversion of a series of 1D dispersion curves.J.Appl.Geophys., 64(3-4): 115-124, doi: 10.1016/j.jappgeo.2008.01.003.

Luo Y H, Xia J H, Liu J P, et al. 2009a. Research on the middle-of-receiver-spread assumption of the MASW method.SoilDyn.Earthq.Eng., 29(1): 71-79, doi: 10.1016/j.soildyn.2008.01.009.

Luo Y H, Xia J H, Xu Y X, et al. 2009b. Dipping-interface mapping using mode-separated Rayleigh waves.PureAppl.Geophys., 166(3): 353-374, doi: 10.1007/s00024-009-0451-z. Mavko G, Mukerji T, Dvorkin J. 1998. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media. Cambridge: Cambridge University Press.

Misiek R, Liebig A, Gyulai A, et al. 1997. A joint inversion algorithm to process geoelectric and surface wave seismic data. Part II: application.Geophys.Prospect., 45(1): 65-85, doi: 10.1046/j.1365-2478.1997.3190241.x.

Morochnik V, Bardet J P. 1996. Viscoelastic approximation of poroelastic media for wave scattering problems.SoilDyn.Earthq.Eng., 15(5): 337-346, doi: 10.1016/0267-7261(96)00002-4.

Paul S. 1976a. On the displacements produced in a porous elastic half-space by an impulsive line load. (Non-dissipative case).PureAppl.Geophys., 114(4): 605-614, doi: 10.1007/BF00875654.

Paul S. 1976b. On the disturbance produced in a semi-infinite poroelastic medium by a surface load.PureAppl.Geophys., 114(4): 615-627, doi: 10.1007/BF00875655.

Philippacopoulos A J. 1988. Lamb′s problem for fluid-saturated, porous media.Bull.Seismol.Soc.Am., 78(2): 908-923.

Picotti S, Carcione J M, Rubino J G, et al. 2010. A viscoelastic representation of wave attenuation in porous media.Comp.Geosci., 36(1): 44-53, doi: 10.1016/j.cageo.2009.07.003.

Picotti S, Carcione J M, Gei D, et al. 2012a. Seismic modeling to monitor CO2geological storage: The Atzbach-Schwanenstadt gas field.J.Geophys.Res., 117(6): B06103, doi: 10.1029/2011JB008540.

Picotti S, Carcione J M, Santos J E. 2012b. Oscillatory numerical experiments in finely layered anisotropic viscoelastic media.Comp.Geosci., 43: 83-89, doi: 10.1016/j.cageo.2012.02.026.

Plona T J. 1980. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies.Appl.Phys.Lett., 36(4): 259-261, doi: 10.1063/1.91445.

Pride S R, Berryman J G. 2003. Linear dynamics of double-porosity dual-permeability materials. II. Fluid transport equations.Phys.Rev.E, 68: 036604.

Pride S R, Berryman J G, Harris J M. 2004. Seismic attenuation due to wave-induced flow.J.Geophys.Res., 109: B01201, doi: 10.1029/2003JB002639.

Rubino J G, Ravazzoli C L, Santos J E. 2009. Equivalent viscoelastic solids for heterogeneous fluid-saturated porous rocks.Geophysics, 74(1): N1-N13, doi: 10.1190/1.3008544. Saenger E H, Schmalholz S, Lambert M, et al. 2009. A passive seismic survey over a gas field: Analysis of low-frequency anomalies.Geophysics, 74(2): O29-O40, doi: 10.1190/1.3078402.

Safani J, O′Neill A, Matsuoka T. 2006. Full SH-wavefield modelling and multiple-mode Love wave inversion.Exp.Geophys., 37(4): 307-321.

Senjuntichai T, Rajapakse R K N D. 1994. Dynamic Green’s functions of homogeneous poroelastic half-plane.J.Eng.Mech., 120(11): 2381-2404, doi: 10.1007/s00707-012-0720-2. Siddharthan R, Zafir Z, Norris G M. 1993. Moving load response of layered soil. I. Formulation.J.Eng.Mech., 119(10): 2052-2071, doi: 10.1061/(ASCE)0733-9399(1993)119:10(2052).

Song X H, Gu H M, Liu J P, et al. 2007. Estimation of shallow subsurface shear-wave velocity by inverting fundamental and higher-mode Rayleigh waves.SoilDyn.Earthq.Eng., 27(7): 599-607, doi: 10.1016/j.soildyn.2006.12.003.

Song Y Y, Castagna J P, Black R A, et al. 1989. Sensitivity of near-surface shear-wave velocity determination from Rayleigh and Love waves. // 59th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 509-512.

Tajuddin M. 1984. Rayleigh waves in a poroelastic half-space.J.Acoust.Soc.Am., 75(3): 682-684, doi: 10.1007/s10659-012-9388-z.

Theodorakopoulos D D. 2003. Dynamic analysis of a poroelastic half-plane soil medium under moving loads.SoilDyn.Earthq.Eng., 23(7): 521-533, doi: 10.1016/S0267-7261(03)00074-5. Theodorakopoulos D D, Chassiakos A P, Beskos D E. 2004. Dynamic effects of moving load on a poroelastic soil medium by an approximate method.Int.J.SolidsStruct., 41(7): 1801-1822, doi: 10.1016/j.ijsolstr.2003.11.009.

Vogelaar B, Smeulders D, Harris J. 2010. Exact expression for the effective acoustics of patchy-saturated rocks.Geophysics, 75(4): N87-N96, doi: 10.1190/1.3463430.

Wang L Z, Chen Y M, Wu S M, et al. 1996. A solution to saturated elastic half-space under harmonic force of low frequency.ShuiliXuebao(in Chinese), (2): 84-88.

Wenzlau F, Müller T M. 2009. Finite-difference modeling of wave propagation and diffusion in poroelastic media.Geophysics, 74(4): T55-T66, doi: 10.1190/1.3122928.

White J E. 1975. Computed seismic speeds and attenuation in rocks with partial gas saturation.Geophysics, 40(2): 224-232, doi: 10.1190/1.1440520.

Winsborrow G, Huws D G, Muyzert E. 2003. Acquisition and inversion of Love wave data to measure the lateral variability of geo-acoustic properties of marine sediments.J.Appl.Geophys., 54(1-2): 71-84, doi: 10.1016/j.jappgeo.2003.07.001.Xia J H, Miller R D, Park C B. 1999. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves.Geophysics, 64(3): 691-700, doi: 10.1190/1.1444578.

Xia J H, Miller R D, Park C B, et al. 2002. Comparing shear-wave velocity profiles from multichannel analysis of surface wave with borehole measurements.SoilDyn.Earthq.Eng., 22(3): 181-190, doi: 10.1016/S0267-7261(02)00008-8.

Xia J H, Miller R D, Park C B, et al. 2003. Inversion of high frequency surface waves with fundamental and higher modes.J.Appl.Geophys., 52(1): 45-57, doi: 10.1016/S0926-9851(02)00239-2.

Xia J H, Chen C, Li P H, et al. 2004. Delineation of a collapse feature in a noisy environment using a multichannel surface wave technique.Géotechnique, 54(1): 17-27, doi: 10.1680/geot.54.1.17.36326.

Xia J H, Xu Y X, Chen C, et al. 2006a. Simple equations guide high-frequency surface-wave investigation techniques.SoilDyn.Earthq.Eng., 26(5): 395-403, doi: 10.1016/j.soildyn.2005.11.001.

Xia J H, Xu Y X, Miller R D, et al. 2006b. Estimation of elastic moduli in a compressible Gibson half-space by inverting Rayleigh-wave phase velocity.SurveysinGeophysics, 27(1): 1-17, doi: 10.1007/s10712-005-7261-3.

Xia J H, Xu Y X, Miller R D. 2007. Generating an image of dispersive energy by frequency decomposition and slant stacking.PureAppl.Geophys., 164(5): 941-956, doi: 10.1007/s00024-007-0204-9.

Xia J H, Miller R D, Xu Y X. 2008. Data-resolution matrix and model-resolution matrix for Rayleigh-wave inversion using a damped least-squares method.PureAppl.Geophys., 165(7): 1227-1248, doi: 10.1007/s00024-008-0364-2.

Xia J H, Miller R D, Xu Y X, et al. 2009. High-frequency Rayleigh-wave method.J.EarthSci., 20(3): 563-579, doi: 10.1007/s12583-009-0047-7.

Xia T D, Chen L Z, Wu S M, et al. 1998. Characteristics of Rayleigh waves in a saturated half space soil.ShuiliXuebao(in Chinese), (2): 47-53.

Xia T X, Yan K Z, Sun M Y. 2004. Propagation of Rayleigh wave in saturated soil layer.ShuiliXuebao(in Chinese), (11): 1-5.

Xu B, Lu J F, Wang J H. 2008. Dynamic response of a layered water-saturated half space to a moving load.Comput.Geotech., 35(1): 1-10, doi: 10.1016/j.compgeo.2007.03.005.

Xu Y X, Xia J H, Miller R D. 2006. Quantitative estimation of minimum offset for multichannel surface-wave survey with actively exciting source.J.Appl.Geophys., 59(2): 117-125, doi: 10.1016/j.jappgeo. 2005. 08.002.

Xu Y X, Xia J H, Miller R D. 2007. Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach.Geophysics, 72(5): SM147-SM153, doi: 10.1190/1.2753831.

Yang J, Wu S M, Chen Y M. 1997. Steady state response of elastic soil layer and saturated layered half-space.ChinaCivilEng.J. (in Chinese), 30(8): 39-48.

Zeng C, Xia J H, Liang Q, et al. 2007. Comparative analysis on sensitivities of Love and Rayleigh waves. // 77th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1138-1141.

Zeng C, Xia J H, Miller R D, et al. 2011. Application of the multiaxial perfectly matched layer (M-PML) to near-surface seismic modeling with Rayleigh waves.Geophysics, 76(3): T43-T52, doi: 10.1190/1.3560019.

Zhang Y, Xu Y X, Xia J H. 2011. Analysis of dispersion and attenuation of surface waves in poroelastic media in the exploration-seismic frequency band.Geophys.J.Int., 187(2): 871-888, doi: 10.1111/j.1365-246X.2011.05168.x. Zhang Y, Xu Y X, Xia J H. 2012. Wave fields and spectra of Rayleigh waves in poroelastic media in the exploration seismic frequency band.Adv.WaterResour., 49: 62-71, doi: 10.1016/j.advwatres.2012.05.014.

Zhang Y, Zhang S X, Xia J H. 2014a. Transient responses of porous media under moving surface impulses.Int.J.SolidsStruct., 51(3-4): 660-672, doi: 10.1016/j.ijsolstr.2013. 10. 031.

Zhang Y, Xu Y X, Xia J H, et al. 2014b. On dispersive propagation of surface waves in patchy saturated porous media.WaveMotion, 51(8): 1225-1236, doi: 10.1016/j.wavemoti.2014.07.007.

Zhang Y, Xu Y X, Xia J H, et al. 2014c. On effective characteristic of Rayleigh surface wave propagation in porous fluid-saturated media at low frequencies.SoilDyn.Earthq.Eng., 57: 94-103.

Zhang Y, Xu Y X, Xia J H, et al. 2014d. Viscoelastic representation of surface waves in patchy saturated poroelastic media.EarthquakeScience, 27(4): 421-431, doi: 10.1007/s11589-013-0049-5.

附中文参考文献

刘凯欣, 刘颖. 2003. 横观各向同性含液饱和多孔介质中瑞利波的特性分析. 力学学报, 35(1): 100-104.

王立忠, 陈云敏, 吴世明等. 1996. 饱和弹性半空间在低频谐和集中力下的积分形式解. 水利学报, (2): 84-88.

夏唐代, 陈龙珠, 吴世明等. 1998. 半空间饱和土中瑞利波特性. 水利学报, (2): 47-53.

夏唐代, 颜可珍, 孙鸣宇. 2004. 饱和土层中瑞利波的传播特性. 水利学报, (11): 1-5.

杨峻, 吴世明, 陈云敏. 1997. 弹性层和饱和半空间体系稳定动力响应. 土木工程学报, 30(8): 39-48.

(本文编辑 何燕)

Characteristics and application of surface wave propagation in fluid-filled porous media

ZHANG Yu1,2,3,4, XU Yi-Xian4,5, XIA Jiang-Hai4, ZHANG Shuang-Xi1,2,3, PING Ping6,4

1SchoolofGeodesyandGeomatics,WuhanUniversity,Wuhan430079,China2KeyLaboratoryofGeospaceEnvironmentandGeodesy,MinistryofEducation,Wuhan430079,China3CollaborativeInnovationCenterofGeospaceInformationScience,WuhanUniversity,Wuhan430079,China4SubsurfaceMulti-scaleImagingLaboratory,ChinaUniversityofGeosciences,Wuhan430074,China5StateKeyLaboratoryofGeologicalProcessesandMineralResources,ChinaUniversityofGeosciences,Wuhan430074,China6StateKeyLaboratoryofGeodesyandEarth′sDynamics,InstituteofGeodesyandGeophysics,ChineseAcademyofSciences,Wuhan430074,China

High frequency surface wave method based on seismic wave propagation in single-phase media has been widely applied for acquiring near surface shear wave velocity in several fields. However, the near surface earth media, consolidated and unconsolidated, for the general hydrogeological conditions, bear plenty of pores. Fluid in pores affects the surface wave propagation in the media remarkably, which is represented in dispersion in velocity and attenuation.

国家重点基础研究计划(2013CB733303)，国家自然科学基金(41304077, 40974079)，中国博士后科学基金(2014T70740, 2013M531744)，教育部地球空间环境与大地测量重点实验室(12-02-03)和湖北省多尺度地下成像重点实验室(SMIL-2014-01)联合资助.

张煜，1982年生，博士，主要从事浅地表地球物理学相关的研究.E-mail：yuz124@gmail.com

10.6038/cjg20150812

P631

2014-12-22，2015-06-11收修定稿

10.1007/s00161-005-0203-y.

张煜, 徐义贤, 夏江海等. 2015. 含流体孔隙介质中面波的传播特性及应用.地球物理学报，58(8):2759-2778,doi:10.6038/cjg20150812.

Zhang Y, Xu Y X, Xia J H, et al. 2015. Characteristics and application of surface wave propagation in fluid-filled porous media.ChineseJ.Geophys. (in Chinese),58(8):2759-2778,doi:10.6038/cjg20150812.