核磁共振与瞬变电磁三维联合解释方法

李貅， 刘文韬， 智庆全， 赵威

1 长安大学地质工程与测绘学院， 西安 710054 2 中国地质科学院地球物理地球化学勘查研究所， 河北廊坊 065000



核磁共振与瞬变电磁三维联合解释方法

李貅1， 刘文韬1， 智庆全2， 赵威1

1 长安大学地质工程与测绘学院， 西安 710054 2 中国地质科学院地球物理地球化学勘查研究所， 河北廊坊 065000

传统核磁共振地下含水量解释多采用基于均匀半空间或层状导电模型的一维反演，分层给出地下含水信息.然而，这些方法忽略了地下复杂电阻率分布信息对结果的影响，也不能很好地反映局部三维含水构造.本文从三维电介质中核磁共振响应的正演理论出发，提出首先利用瞬变电磁数据进行基于等效导电平面法的快速电阻率成像，然后将成像结果作为核磁共振三维反演的电性模型，进行联合解释.激发磁场的分布采用有限元法直接求解，通过引入伪δ源实现电流源的加载，并强加散度条件排除了三维磁场模拟中“弱解”的影响.针对核磁共振灵敏度矩阵的病态性和数据中存在的干扰信号，提出考虑罚项的非线性拟合目标函数，利用线性化方法进行核磁共振反演.模型数据表明该方法能较准确反映地下三维含水构造，实测算例进一步证明了方法的有效性.本研究将促使核磁共振方法在岩溶、裂隙水、孤立水体等复杂水文地质条件及隧道、矿井灾害水源探测等方面得到有效应用.

核磁共振； 瞬变电磁； 等效导电平面； 三维联合解释

1 引言

核磁共振(Nuclear Magnetic Resonance，NMR)，作为目前世界上唯一直接探测地下水体的地球物理方法(林君等, 2011;潘玉玲和张昌达, 2000)，因具有直接确定含水体的空间分布和水量的能力，近年来得到了广泛的应用(潘玉玲等, 2000;Chalikakis et al.,2008;Legchenko et al.,2010;Lubczynski and Roy,2005;李振宇等, 2003;林君等, 2011;万乐和潘玉玲, 1999).目前核磁共振一维正反演理论已比较成熟(戴苗等, 2009;林婷婷等,2013;Legchenkoand Shushakov, 1998; Guillen and Legchenko, 2002; Weichman et al., 2002; 翁爱华等, 2007)，即假设地下水呈层状分布，分层给出地下含水信息.对于近似水平层状分布的地下水，目前解释方法能取得较好效果，然而对于地下岩溶、裂隙水、孤立水体等局部三维含水构造，由于不满足层状分布，强行将地下含水构造当作一维层状模型来处理往往会产生较大误差，甚至得不到合理的结果(陈斌等,2014).为拓展核磁共振找水的应用范围，实现复杂水文地质环境下的有效探测，应开展NMR技术的三维正反演研究.

对于这一问题，Warsa和Grandis(2012)对均匀半空间下三维含水构造进行了NMR正演，Warsa等(2014)又在之前研究基础上进行了二维、三维含水构造的反演，模型算例表明三维反演能够实现对三维含水构造的较好分辨.此外，国内王鹏(2014)也对均匀半空间下三维含水体进行了NMR正演，并对几种常见三维含水构造响应特征进行了一定讨论.但上述研究均基于均匀半空间模型，没有考虑地下电阻率信息的影响，而实际中地下电阻率信息是影响核磁共振探测效果的一个重要因素(翁爱华等,2007;Braun and Yaramanci, 2011).传统的NMR数据反演方法，通常依据地质情况估计一个等效半空间模型，这导致反演结果受人为因素影响(万玲等, 2013)，对于复杂三维导电模型，这种等效将严重偏离真实地质构造.因此，要进行核磁共振的精确解释，必须首先获得合理的电性模型.

国际上相关研究起步于2002年，Hertrich和Yaramanci(2002)曾利用模拟退火方法实现了核磁共振方法和垂直电测深方法的联合反演，利用电测深法获得了电性模型，但电测深法为了获取与核磁共振相同深度的电阻率一般需要敷设很长的供电导线，且对地形等工作条件要求较高，不利于野外施工.Braun等(2005)，Braun和Yaramanci(2008)尝试了利用核磁共振信号的相位信息进行反演获得电性分布的方法，并在理论模型试验上取得了良好的效果.但在实际工作中，由于仪器和环境干扰的影响，相位信息往往信噪比更低，利用相位信息的反演结果可信度不高.为了克服这些困难，有些学者着手研究了瞬变电磁和核磁共振方法的联合解释技术.

瞬变电磁法(Transient Electromagnetic，TEM)是一种电磁感应方法，它利用不接地回线或接地线源发送一次脉冲电磁场，导电介质内部受感应产生涡旋电流，在一次脉冲电磁场间歇期间，涡旋电流产生的二次磁场不会随一次场消失而立即消失，利用线圈或接地电极观测二次磁场，研究其与时间的变化关系，从而确定介质的电性分布结构及空间形态.瞬变电磁法具有场源灵活、方法多样以及稳定高效等优点，相比于电测深法而言，瞬变电磁法不需要敷设较长的导线即可达到相当的探测深度，对工作环境要求相对较低.Legchenko(2009)研究了核磁共振和瞬变电磁的联合探测方法，结合两种方法各自的优势，较为准确地对地下含水层进行了圈定.万玲等(2013)联用瞬变电磁数据和核磁共振数据进行了一维联合反演，模型测试和实测数据处理结果表明，联合反演方法对于含水层位置和界面的圈定更为准确.但联合反演方法以瞬变电磁法和核磁共振法的正演为基础，而三维瞬变电磁正演相比核磁共振而言，需要时间远远为多.因此目前来看，在三维核磁共振解释中直接进行联合反演，仍是不现实的.

为了综合核磁共振和瞬变电磁法各自的优势，实现核磁共振和瞬变电磁三维联合解释，并避开瞬变电磁三维正演这一极为耗费时间成本的过程，本文提出，在联合解释工作中，可首先依赖基于导电平面法的快速电阻率成像技术从瞬变电磁数据中提取电性信息，以此作为电性模型，利用三维有限元法计算介质中各处激发磁场值，进而实现核磁共振三维正演；然后进行核磁共振三维反演，求取含水率分布；考虑灵敏度矩阵的奇异性和数据包含误差，引入带有罚项的最小二乘目标函数.

2 三维电介质下NMR正演

2.1 NMR信号初始振幅的计算

(1)

(2)其中，M0为氢原子核磁化强度；γ=2.675×108s-1T-1为氢质子磁旋比；n(r)为空间r(x,y,z)位置处的含水率；ρ(r)为空间r(x,y,z)位置处电阻率；q=I0·τ为发射脉冲矩；K3D(q,ρ(r),r)为三维核函数，代表接收线圈对地下r(x,y,z)处含水体的灵敏度大小；B⊥为激发磁场BT垂直于地磁场B0的分量；E0为NMR信号初始振幅，其大小与被激发的地下氢质子数量成正比.

建立如图1a直角坐标系，X轴指向地理正北方向，Y轴指向地理正东，Z轴垂直向下，D为地磁偏角，I为地磁倾角，则B⊥可利用BT进行两次坐标系旋转的方法求得(林君等，2013).记BT在新坐标系下为

B″=B″xex+B″yey+B″zez,

(3)

B″与BT关系可用旋转矩阵RI和RD表示

B″=RIRDBT,

(4)

(5)此时X方向与地磁场方向重合，于是B⊥可表示为

(6)

(7)其中，Δxi,Δyj,Δzk分别为点r(x,y,z)位置剖分单元在X,Y,Z方向上长度；N,M,L分别为X,Y,Z方向剖分单元个数.

选择一系列递增的脉冲矩q，观测初始振幅E0随脉冲矩q的变化，可反映由浅到深不同深度含水量分布.根据(1)—(7)式可知，在观测参数确定的情况下，计算响应信号初始振幅E0的关键是首先获得地下激发磁场的分布.

2.2 激发磁场分布的求取

在仅存在外加电性源、时谐情况下，假定谐变因子为eiω t，电磁场所满足的Maxwell方程组为

(8)

式中，ε为介质的介电常数，σ是电导率，μ是磁导率，ω为激励电性源的圆频率，i为虚数单位，t为时间，E和H分别为电场和磁场矢量，Js为外加电流源的电流密度.利用节点有限元法求解(8)式时，为了规避计算电流密度的旋度或电场法向不连续的问题，常先计算电场或矢量势，然后通过求导来获取磁场值.然而，由于求导运算，计算得出的磁场值将比直接用有限元求解的量精度低.本文拟直接利用有限元法计算磁场值，并引入伪δ源来解决电流密度的旋度计算问题.由于不存在磁荷和面电流密度，磁场在内部电性界面上，同时具有法向和切向连续性.为通用起见，在外边界S2上给定磁场的第三类边界条件为

(9)

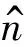
(10)

其中，k2=-iωμσ.

根据变分原理，通过求解泛函(11)的驻点，能够获得满足方程(10)和边界条件(9)的磁场解

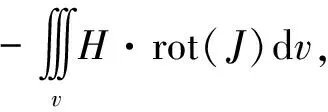
(11)

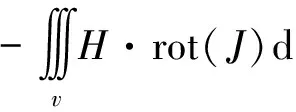
(12)

对求解区域进行剖分以离散(12)式，假定剖分单元内部物性均匀，并设单元节点i上的磁场三个分量分别为Hxi,Hyi,Hzi，则对剖分后的所有单元，求解变分问题(12)的驻点等价于求解方程组

(13)

其中，n为剖分单元个数，e为单元编号.

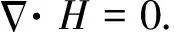
(14)令R=rot(J)，于是在每个小单元内有线性方程组

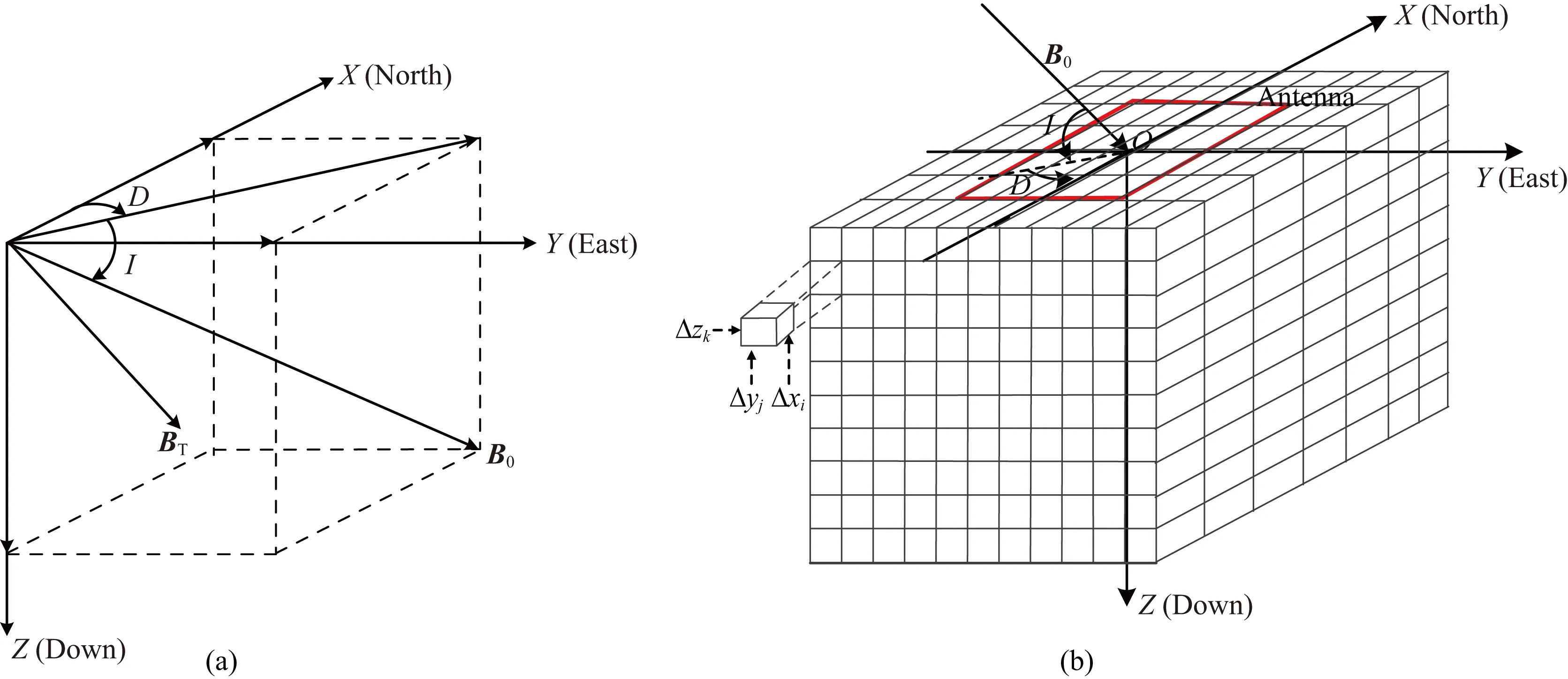
图1 坐标系示意图(a)坐标系与地理方位关系示意图；(b)网格剖分示意图.Fig.1 Diagram of coordinates(a) Relationship between coordinates and the geographic orientation; (b) Mesh subdivision.

图2 均匀半空间模型激发磁场强度有限元解和数字滤波解比较(a) Hx实部; (b) Hz实部;(c) Hx虚部;(d) Hz虚部.Fig.2 Comparison ofFEM solutions and digital filtering solutions of excitation magnetic field for homogenous half space model(a) Real of Hx; (b) Real of Hz; (c) Imag of Hx; (d) Imag of Hz.

(15)

源的加载采用如(16)式Herrmann(1979)提出的伪δ函数来等效场源的作用，将源分布于一定范围内，避免在源点处产生奇异性，直接进行总场的求解.细导线源的效应，可利用伪δ函数进行等效.如空间(x0,y0,z0)处电流强度为I、沿I方向的导线源，其电流密度的分布可写为Jy=Iδs(x-x0)δs(z-z0).式(15)中对电流密度求旋度的运算，可转换为对伪δ函数的导数运算.将四条等效导线源沿着一致电流方向围成一个方形，即完成对NMR工作中常用的方形回线源加载.

(16)

式中，τ是控制源分布宽度和幅值的参数，x为某一空间维度的坐标，x0为源所在位置即奇异点的坐标值.

采用上述方法，计算了边长100m发射线圈在电阻率为100Ωm的均匀半空间上产生的磁场，并在地表沿x轴布置一条测线，与数字滤波解进行对比，计算结果如图2所示，可见除导线附近位置，有限元计算结果与数字滤波解基本一致.最后，激发磁场(磁感应强度)可采用(17)式求得

BT=μH.

(17)

3 介质导电性对核函数的影响分析

核磁共振响应核函数代表接收线圈对地下含水体灵敏度的大小，为研究介质电阻率对核函数的影响，本文对核磁共振响应三维核函数进行了仿真.采用100m单匝方形同一线圈，源中心位于地面(0,0)处，发射脉冲矩范围0.05～15A·s，地磁场强度48000nT，地磁倾角60°N，地磁偏角0°，拉莫尔频率2044Hz.首先分别对电阻率为5、10、50、100、300Ωm和1000Ωm均匀半空间模型进行计算，分别记为a—f模型，图3所示为其三维核函数仿真结果，图中仅列出一个脉冲矩(q=2.5 A·s)的计算结果.从图中可以看出介质电阻率大小直接影响核函数分布，介质电阻率减小时，相同脉冲矩所能激发的影响范围相应减小，这是因为电磁波在低电阻率介质中衰减快，电磁波能量难以穿透到深部.在当前线圈边长(l=100 m)下，对于电阻率小于50 Ωm低阻介质，其对核函数分布的影响尤为明显；而后随着介质电阻率增大，其对核函数的影响逐渐减弱；当电阻率大于100 Ωm时，其对核函数分布的影响从图上几乎难以分辨.

这种特性也直观体现在核磁共振信号初始振幅E0上.假设地下有一水平方向50 m×50 m，厚20 m的含水体，含水体中心位于(0，0，30 m)处，含水率30%，图4a所示即为不同介质电阻率下同一线圈采集得到的核磁共振初始振幅E0的仿真结果.当均匀半空间电阻率小于50 Ωm时，不同介质电阻率下初始振幅信号差别明显，随着介质电阻率减小，初始振幅E0最大值减小明显，最大值出现对应脉冲矩q逐渐增大；随着介质电阻率增大，介质电阻率对初始振幅信号的影响逐渐减小，当介质电阻率达300 Ωm，与1000 Ωm情况进行对比，相同脉冲矩对应的初始振幅之差最大值不足1.5 nV.

可以看出，低阻背景对核磁共振信号影响明显，为进一步讨论局部导电介质对核磁共振响应核函数的影响大小，在100 Ωm均匀半空间介质中，设计三种不同埋深和规模的低阻导电体模型，低阻体电阻率均为5 Ωm，分别记为g—i模型.模型g：低阻导电体尺寸：长50 m，宽50 m，厚20 m；导电体中心位置：(0,0,30 m).模型h：低阻导电体尺寸：长20 m，宽20 m，厚10 m；导电体中心位置：(0,0,30 m).模型i：低阻导电体尺寸：长50 m，宽50 m，厚20 m；导电体中心位置：(0,0,70 m).图5所示为其三维核函数仿真结果，为便于比较也列出脉冲矩q=2.5 A·s的计算结果，与100 Ωm均匀半空间模型对比可以看出，对于浅层低阻异常体，当异常体的规模较大(横向尺寸为线圈边长1/2)时，其对核函数的影响较大，而当异常体的规模较小(横向尺寸为线圈边长1/5)时，其对核函数的影响较小.对于深层低阻异常体，即使异常体较大规模(横向尺寸为线圈边长1/2)，其对核函数的影响也较小.采用上述相同的含水体，对这三种局部异常体模型的初始振幅E0进行仿真计算，结果如图4b，与100 Ωm均匀半空间模型进行对比，同样的特征也体现在初始振幅上，浅层规模较大的局部低阻异常体对初始振幅信号影响显著，而规模较小或位于深部的低阻异常体对初始振幅信号影响较小，这是因为核磁共振信号是来自频域激发磁场对于宏观磁矩的“扳倒”作用，而当局部异常体的规模较小或埋藏较深时，对于频域激发磁场的影响不大.综上，核磁共振响应对低阻背景和规模较大的浅层低阻异常体表现较为敏感，而对高阻背景、规模较小局部低阻异常体或深部的局部异常体表现不敏感.

图3 均匀半空间三维核函数分布 (X-Z方向切片)介质电阻率为 a-5 Ωm； b-10 Ωm；c-50 Ωm； d-100 Ωm； e-300 Ωm； f-1000 Ωm.Fig.3 3D kernel function distribution for homogenous half space model (X-Z slice)Resistivity a-5 Ωm； b-10 Ωm； c-50 Ωm； d-100 Ωm； e-300 Ωm； f-1000 Ωm.

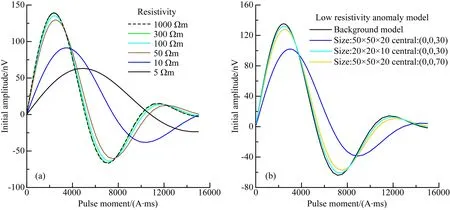
图4 不同介质电阻率下E0-q曲线(含水体参数：长50 m,宽50 m, 厚20 m, 含水率30%，中心点位置(0,0,30 m))(a) 不同均匀半空间模型计算结果对比； (b) 100 Ωm背景介质中不同尺寸低阻异常体模型计算结果对比.Fig.4 E0-q curves of different resistivity(water-bearing parameters: length 50 m, width 50 m, thickness 20 m, water content 30%, central position (0,0,30 m))(a)Results of different homogenous half space models；(b) Results of differentsizes of low resistivity anomaly under 100 Ωm resistivity background.

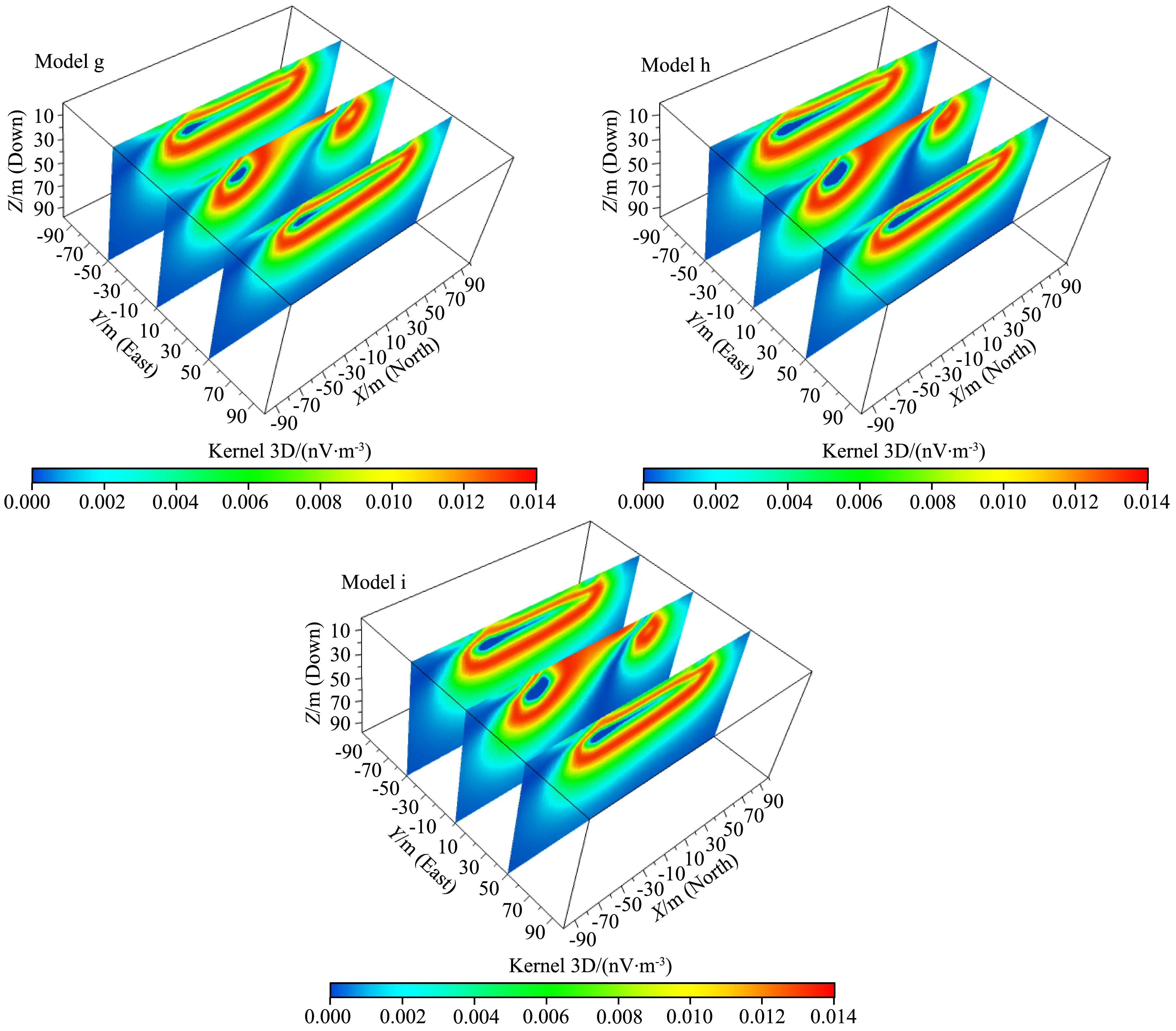
图5 不同尺寸低阻异常体模型三维核函数分布(X-Z方向切片，背景电阻率100 Ωm，低阻体电阻率5 Ωm)g低阻体尺寸：长50 m,宽50 m,厚20 m；异常体中心：(0,0,30 m);h低阻体尺寸：长20 m,宽20 m,厚10 m；异常体中心：(0,0,30 m); i低阻体尺寸：长50 m,宽50 m,厚20 m;异常体中心：(0,0,70 m).Fig.5 3-D kernel function distribution for different sizes of low resistivity anomaly (X-Z slice, background resistivity 100 Ωm, anomalous resistivity 5 Ωm)g-Anomalous model size: length 50 m, width 50 m, thickness 20 m; central position (0,0,30 m); h-Anomalous model size: length 20 m, width 20 m, thickness 10 m; central position (0,0,30 m); i-Anomalous model size: length 50 m, width 50 m, thickness 20 m; central position (0,0,70 m).

4 NMR-TEM联合解释方法

前节指出，低阻背景和浅部规模较大的低阻异常体对核磁共振响应核函数分布较大影响，核磁共振解释中应考虑介质的电性分布的影响.获取地下介质的电性分布可依靠电磁法反演技术，但目前而言电磁法三维正演均需较长的时间，若在核磁共振解释中引入三维电磁法反演，将严重影响解释工作的效率.考虑核磁共振响应对规模不大的局部导电异常体不敏感，并无必要在核磁共振解释中获取完全精确的电性分布.本文采用瞬变电磁法对勘探区域进行电性分布探测，利用基于导电平面的快速电阻率成像技术近似地获取勘探区域的电性分布，然后以此作为电性模型进行核磁共振三维反演，获得地下含水量分布信息.

4.1 等效导电平面快速成像技术基本原理

等效导电平面法是一种瞬变电磁探测的近似解释方法，它是根据视纵向电导曲线进行快速、直观电性介质成像的(Tartaras et al., 2000).在瞬变电磁法中，信号接收装置是由多匝导线绕成的线圈或探头，接收到的是二次磁场随时间的变化率.我们将某一时刻观测的二次场响应信号等同地认为是由某一深度的一个虚拟源(导电薄板)产生的信号，另一时刻观测到的感应信号又可以等同地认为是另外一个深度的另外一个虚拟源所产生的信号，这样，不同时间延迟的观测数据就会对应不同深度的导电薄板.依据等效导电平面理论有

(18)

其中，S为纵向电导，K为与发射接收有关的常数，I为发射电流大小，a为发射回线半径，F为一个与时间和电导都有关的函数.F的表达式为

(19)

h为薄板深度，t为接收时刻.纵向电导S可依(20)式求取

(20)

显见，(20)式是关于纵向电导S的非线性方程，求解该方程即得纵向电导S.根据纵向电导的定义，可得电阻率值ρτ(h)=dh/dS，对应深度为

4.2 核磁共振三维反演方法

如图1b，当按照设定的研究尺度，将研究空间离散化为网格单元，各网格内部物性均匀分布时，核磁共振初始振幅计算公式可用(7)式表示，为便于书写,(7)式也可简写为：

(21)

其中，N为剖分单元的个数，Kj为第j个单元的核函数，nj为第j个单元的含水率值.

在多个脉冲矩激发下，(21)式可以矩阵形式表示：

K·n=E0,

(22)

φ(n)=‖Kn-E‖L2+α‖n‖L2,

(23)

其中，‖‖L2为二范数算子，α为非负正则化参数.使目标函数(23)最小化即可获得矩阵方程(22)在最小范数罚项下的最优解.目标函数极小值本文采用信赖域方法进行求解，反演初值依据电性模型假设电阻率与含水率线性反相关近似给出.

4.3 TEM-NMR联合解释流程

联合解释流程框图如图6所示.其具体操作步骤如下：

(1) 导入NMR、TEM实测数据及工作参数装置；

(2) 对TEM数据采用等效导电平面法获得电性模型，并在电阻率与含水率的线性反相关的近似假设下，给出含水率反演初始模型；

(3) 基于获得的电性模型，采用三维有限元方法计算B⊥，从而实现NMR的正演计算；

(4) 对目标函数采用信赖域方法进行迭代反演，直到目标函数值小于给定值或达到迭代次数，输出反演结果.

图6 TEM-NMR联合解释流程框图Fig.6 Flow of TEM-NMR joint interpretation

5 仿真模型算例

5.1 均匀半空间电性模型

为验证核磁共振三维反演方法的有效性，首先对均匀半空间电性模型下核磁共振数据进行核磁共振单独反演. NMR数据在如下条件下获得：边长100 m的单匝方形线圈，采用收发共线圈方式；均匀半空间电阻率200 Ωm，地磁场强度48000 nT，地磁倾角60°N，地磁偏角0°，拉莫尔频率2044 Hz，最大激发脉冲矩15 A·s；含水体模型(图7a)参数：长60 m，宽60 m，厚25 m，中心位于(0，0,27.5 m)，含水率为30%；地面布置测点25个，测点沿X，Y方向间距均为50 m，对X为-100～100 m，Y为-100～100 m的范围进行核磁共振探测，仿真初始振幅曲线如图7e中实线(以X=0 m测线上5个点为例).

在XYZ方向以10 m×10 m×5 m网格间隔对探测区域进行离散，分别以200 Ωm，50 Ωm，20 Ωm的半空间电性模型，采用NMR数据进行单独反演，结果分别如图7b、7c、7d所示.可见在反演所采用的电性模型与真实电性情况较相符时，反演结果与实际含水体边界和含水量吻合较好(图7b)，说明在给定合理电性模型前提下，本文核磁共振三维反演方法可以取得较好的反演效果.另一方面，从图7c、7d反演结果可以看出，电性模型影响反演结果的准确度，反演时电性模型与真实电性情况相差越大，反演结果与真实含水边界及水量偏离越大.

5.2 单个含水体模型

考虑含水体的电性差异，把5.1节含水体电阻率改为10 Ωm，保持其他模型参数和观测参数不变，核磁共振初始振幅如图8a中实线所示，以X=0 m测线上5个点为例；瞬变电磁采用边长30 m的方形发射线圈，中心回线工作方式，地面布置测点49个，测点X，Y方向间距均为30 m，对X为-90～90 m，Y为-90～90 m的范围进行观测，瞬变电磁仿真数据采用三维时域有限差分方法(孙怀凤等，2013)获得.对瞬变电磁仿真数据进行等效导电平面成像，结果如图8a所示，与含水体模型(图7a)对比可以看出成像结果基本反映出低阻含水体轮廓且视电阻率值与真实电阻率值较为接近，可为核磁共振三维反演提供合理的电性模型.

在XYZ方向以10 m×10 m×5 m网格间隔对探测区域进行离散.首先，采用均匀半空间电性模型进行核磁共振单独反演，电性模型给定为200 Ωm的半空间，反演拟合曲线如图8d虚线所示，可见反演含水率计算的初始振幅与真实初始振幅拟合得很好，但从含水率反演结果来看(图8b)，虽基本反映出真实含水体轮廓，但含水体位置偏深，且浅部出现一个假含水薄层，局部含水率与真实含水率偏差较大.

对于相同的离散网格，采用电阻率成像结果作为电性模型进行核磁共振反演，反演拟合曲线(图8d中点划线)与真实曲线同样吻合很好，含水率反演结果来看(图8c)，反演含水体位置与真实含水体基本一致，与直接采用半空间作为电性模型进行反演的结果对比，可以看出反演精度有较大改善.

5.3 多个含水体模型

为进一步验证联合解释方法进行含水率三维解

图7 均匀半空间模型核磁共振单独反演结果(a)含水体模型；(b)200 Ωm半空间反演电性模型下反演结果；(c)50 Ωm半空间反演电性模型下反演结果；(d)20 Ωm半空间反演电性模型下反演结果；(e)初始振幅曲线对比.Fig.7 Single inversion results of NMR data based on homogenous half space model(a) Water-bearing model； (b) Inversion resultsunder the half space electric model of 200 Ωm； (c) Inversion results under the half space electric model of 50 Ωm； (d) Inversion results under the half space electric model of 20 Ωm； (e) Initial amplitude curves comparison.

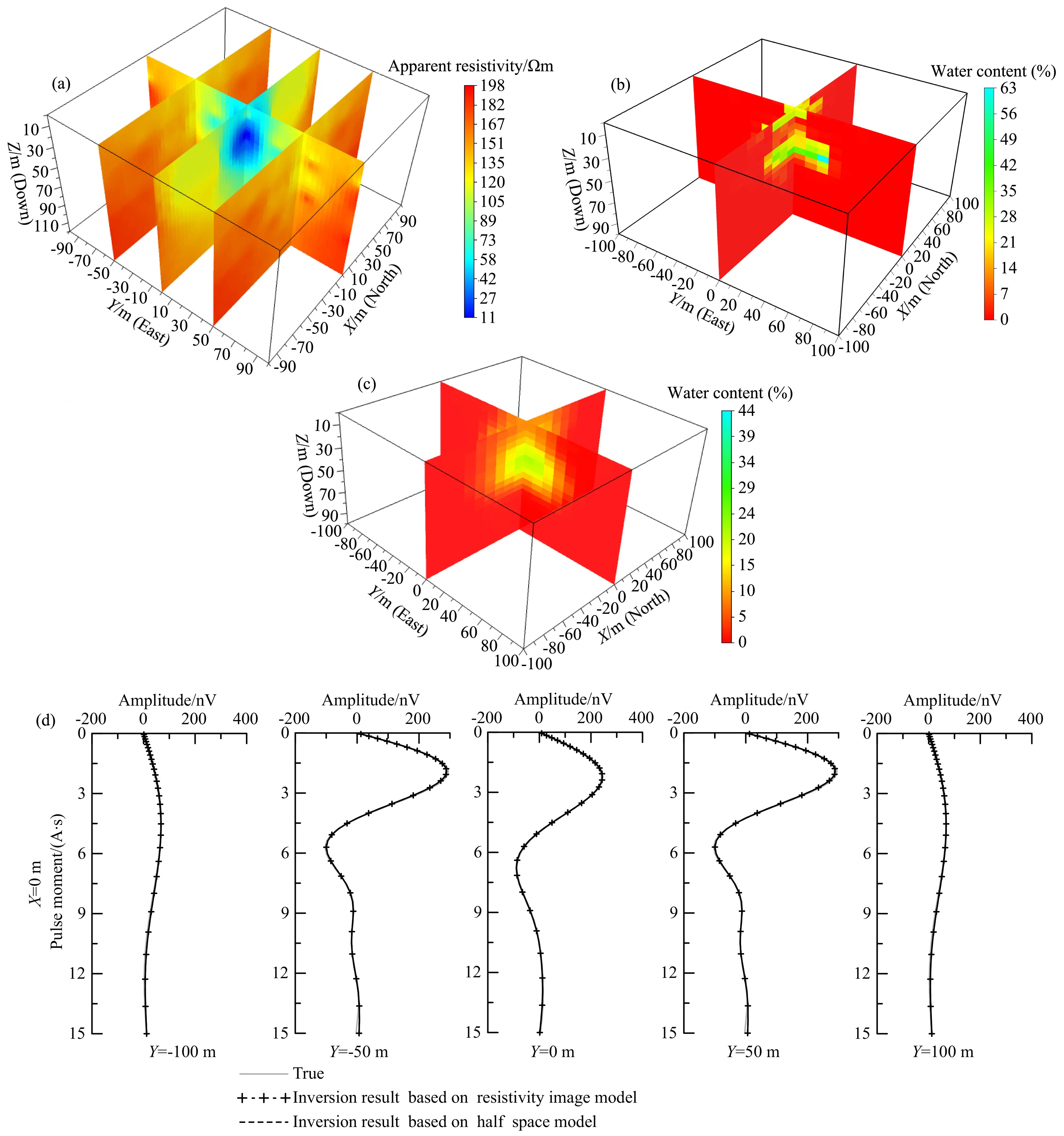
图8 单个含水体模型及其反演结果(a) 电阻率成像结果; (b) 半空间电性模型含水率反演结果; (c) 成像电阻率模型含水率反演结果; (d) 初始振幅曲线对比.Fig.8 Modeling of single water bearing body and inversion results(a) Resistivity image result; (b) Inversion result of water content based on homogenous half space model; (c) Inversion result of water content based on resistivity image model; (d) Initial amplitude curvescomparison.

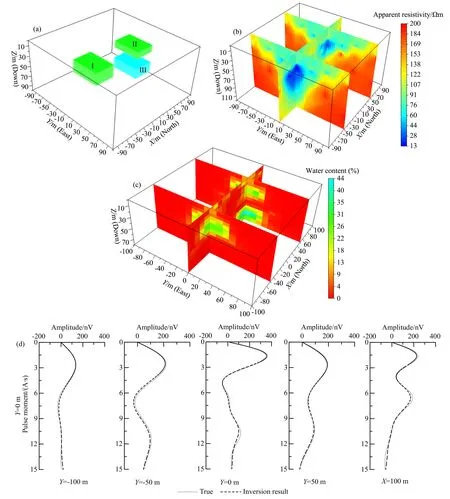
图9 多个含水体模型设定与反演结果(a) 含水体模型图; (b) 电阻率成像结果; (c) 成像电阻率模型含水率反演结果; (d) 初始振幅曲线对比.Fig.9 Modeling of multi-water bearing bodies and inversion results(a) Water-bearing model; (b) Resistivity image result; (c) Inversion result of water content based on resistivity image model; (d) Initial amplitude curvescomparison.

图10 (a)电阻率成像结果;(b)核磁共振反演结果Fig.10 (a) Result of resistivity imaging; (b) Result of NMR inversion

释的效果，设计一个更为复杂的地下含水体模型(图9a)，模型参数如表1，地磁场参数、探测方式及参数保持不变，瞬变电磁仿真数据等效导电平面成像结果如图9b所示，从图中可以看出视电阻率对含水体Ⅰ刻画最清楚，含水体Ⅱ也有较明显的反映，而深部含水体在图中反映不明显，这说明瞬变电磁法随着目标深度增加探测能力逐渐减弱.然而，第3节中指出局部深层低阻体对核磁共振响应核函数的影响很小，对核磁共振初始振幅信号的影响几可忽略，因此该成像结果仍可作为核磁共振反演合理的电性模型.

以成像结果作为电性模型进行核磁共振初始振幅反演结果如图9c所示，含水体Ⅰ的反演结果能够准确反映原始模型，说明合理的电性模型可明显提高反演精度.受电性模型影响，含水体Ⅱ和含水体Ⅲ反演效果比含水体Ⅰ稍差，但也较准确反映出真实含水体位置和水量，且在垂向上两个含水体能清晰可辨，再次说明了联合解释方法的有效性.

表1 多个含水体模型Table 1 Modeling of multi-water bearing bodies

6 实测资料试验

为验证本文提出联合解释技术对于实测数据的有效性，我们以雅砻江锦屏水电站辅助涵洞隧道的探测结果为实例进行模型测试.锦屏水电枢纽工程辅助洞位于四川省凉山彝族自治州的木里、盐源、冕宁三县交界处的雅砻江干流锦屏大河湾上，地形起伏较大.为探测隧道开挖前方充水裂隙的存在，采用中心回线装置进行了瞬变电磁探测，并利用等效导电平面成像技术进行解释，如图10a所示(Z轴绘图缩放比3∶1).根据成像结果可以判断，在掌子面前方20～50 m处范围内存在低阻异常，可能为充水裂隙发育带.以此电性模型为基础进行核磁共振反演，并勾绘含水率为10%的等值面如图10b.由图可见，核磁共振反演的充水带范围和低电阻率异常具有较好的对应关系.同时表明含水率较高的充水带位于35～45 m范围，而20～30 m的低阻异常充水率并不高，可能仅仅是局部电性异常的反映.后期的掘进结果表明，联合解释方法对于含水带的圈定是准确的.

7 结论

(1) 核磁共振响应的计算，需要预先求得频域激发磁场的分布.本文从谐变磁场所满足的变分问题出发，通过求变分的驻点得到了有限元方程.引入伪δ解决了细导线中电流密度的旋度计算问题，实现了电流源的直接加载，避开了二次场算法.对于三维电磁场有限元求解中可能存在的“伪解”问题，采用了在变分中强加散度罚项的方法，以减小“伪解”对计算结果的影响.与数字滤波解对比表明，文中三维频率域正演方法具有较高的精度.

(2) 核磁共振响应核函数代表接收线圈对地下含水体灵敏度大小，通过模型计算研究了介质电阻率对核磁共振响应核函数分布的影响规律.计算结果表明，核磁共振响应核函数对高阻介质不敏感，但低阻背景或浅部较大尺度的低阻体对核磁共振响应核函数的影响是显著的.因此，进行核磁共振解释工作时，应考虑电性分布的影响.

(3) 在分析介质电阻率对核磁共振响应核函数影响的基础上，提出了利用瞬变电磁信号进行电阻率成像并将其作为核磁共振三维反演的电性模型的联合解释方法.考虑到实际核磁共振数据包含干扰信号和空间离散程度带来的误差，采用包含罚项的最小二乘目标函数，利用线性化方法进行核磁共振反演.

(4) 利用仿真模型和实际观测数据进行了瞬变电磁和核磁共振的联合解释，均匀半空间模型验证了核磁共振三维反演方法的有效性，单个含水体模型与多个含水体模型的解释结果均表明，联合解释方法能更好地反映出地下含水率分布，相比传统单独核磁共振反演优势明显.实测资料测试表明本文所提出联合解释方法综合利用了瞬变电磁法的快速成像和核磁共振方法的直接找水特点，低阻异常带和含水带互相印证,实现了对地下含水体较为精确的定位.

Braun M, Hertrich M, Yaramanci U. 2005. Study on complex inversion of magnetic resonance sounding signals.NearSurfaceGeophysics, 3(3): 155-163, doi: 10.3997/1873-0604.2005011.Braun M, Yaramanci U. 2008. Inversion of resistivity in magnetic resonance sounding.JournalofAppliedGeophysics, 66(3-4): 151-164, doi: 10.1016/j.jappgeo.2007.12.004.

Braun M, Yaramanci U. 2011. Evaluation of the influence of 2-D electrical resistivity on magnetic resonance sounding.JournalofEnvironmental&EngineeringGeophysics, 16(3): 95-103.

Chalikakis K, Nielsen M R, Legchenko A. 2008. MRS applicability for a study of glacial sedimentary aquifers in Central Jutland, Denmark.JournalofAppliedGeophysics, 66(3-4): 176-187, doi: 10.1016/j.jappgeo.2007.11.005.

Chen B, Hu X Y, Liu D H, et al. 2014. The development history and new progress of magnetic resonance sounding technique.ProgressinGeophysics(in Chinese), 29(2): 650-659, doi: 10.6038/pg20140224.

Dai M, Hu X Y, Wu H B, et al. 2009. Inversion of surface nuclear magnetic resonance.ChineseJ.Geophys. (in Chinese), 52(10): 2676-2682, doi: 10.3969/j.issn.0001-5733.2009.10.028.Guillen A, Legchenko A. 2002. Inversion of surface nuclear magnetic resonance data by an adapted Monte Carlo method applied to water resource characterization.JournalofAppliedGeophysics, 50(1-2): 193-205, doi: 10.1016/S0926-9851(02)00139-8.

Herrmann R B. 1979. SH-wave generation by dislocation sources—a numerical study.BulletinoftheSeismologicalSocietyofAmerica, 69(1): 1-15.

Hertrich M, Yaramanci U. 2002. Joint inversion of surface nuclear magnetic resonance and vertical electrical sounding.JournalofAppliedGeophysics, 50(1-2): 179-191, doi: 10.1016/S0926-9851(02)00138-6.

Legchenko A, Ezersky M, Camerlynck C, et al. 2009. Joint use of TEM and MRS methods in a complex geological setting.ComptesRendusGeoscience, 341(10-11): 908-917, doi: 10.1016/j.crte.2009.07.013.

Legchenko A, Vouillamoz J M, Roy J. 2010. Application of the magnetic resonance sounding method to the investigation of aquifers in the presence of magnetic materials.Geophysics, 75(6):L91-L100, doi: 10.1190/1.3494596.

Legchenko A V, Shushakov O A. 1998. Inversion of surface NMR data.Geophysics, 63(1): 75-84, doi: 10.1190/1.444329.

Li Z Y, Pan Y L, Zhang B, et al. 2003. Using NMR method research the hydrogeology problems and practical examples.Hydrogeology&EngineeringGeology(in Chinese), 30(4): 50-54, doi: 10.3969/j.issn.1000-3665.2003.04.011.

Lin J, Duan Q M, Wang Y J, et al. 2011. Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and Its Applications (in Chinese). Beijing: Science Press.

Lin J, Jiang C D, Lin T T, et al. 2013. Underground magnetic resonance sounding (UMRS) for detection of disastrous water in mining and tunneling.ChineseJ.Geophys. (in Chinese), 56(11): 3619-3628, doi: 10.6038/cjg20131103.

Lin T T, Hui F, Jiang C D, et al. 2013. Layered multi-exponential inversion method on surface magnetic resonance sounding dataset.ChineseJ.Geophys. (in Chinese), 56(8): 2849-2861, doi: 10.6038/cjg20130833.

Lubczynski M, Roy J. 2005. MRS contribution to hydrogeological system parametrization.NearSurfaceGeophysics, 3(3): 131-139, doi: 10.3997/1873-0604.2005009.

Pan Y L, Zhang C D. 2000. The Theory and Methods of Water Detecting (in Chinese). Wuhan: China University of Geosciences Press.Pan Y L, Li Z Y, Wan L, et al. 2000. Detecting bedrock fissure water with nuclear magnetic resonance (NMR) method.CTTheoryandApplications(in Chinese), 9(1): 22-25.

Sun H F, Li X, Li S C, et al. 2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time.ChineseJ.Geophys. (in Chinese), 56(3): 1049-1064, doi: 10.6038/cjg20130333.

Tartaras E, Zhdanov M S, Wada K, et al. 2000. Fast imaging of TDEM data based on S-inversion.JournalofAppliedGeophysics, 43(1): 15-32, doi: 10.1016/S0926-9851(99)00030-0. Wan L, Pan Y T. 1999. Detecting of karst water in China with nuclear magnetic resonance (NMR) method.CTTheoryandApplications(in Chinese), 8(3): 15-19.

Wan L, Lin T T, Lin J, et al. 2013. Joint inversion of MRS and TEM data based on adaptive genetic algorithm.ChineseJ.Geophys. (in Chinese), 56(11): 3728-3740, doi: 10.6038/cjg20131114.

Wang P. 2014. The MRS response of 3D model in uniformity medium.CTTheoryandApplications(in Chinese), 23(4): 569-578.

Warsa, Grandis H. 2012. Sensitivity study of 3-D modeling for multi-D inversion of surface NMR. ∥ International Conference on Physics and Its Applications: (ICPAP 2011).Bandung, Indonesia: AIP Publishing, 1454: 130-133, doi: 10.1063/1.4730704.

Warsa, Grandis H, Parnadi W W, et al. 2014. Multi-dimensional inversion modeling of surface nuclear magnetic resonance (SNMR) data for groundwater exploration.JournalofEngineeringandTechnologicalSciences, 46(2): 123-140. Weichman P B, Lun D R, Ritzwoller M H, et al. 2002. Study of surface nuclear magnetic resonance inverse problems.JournalofAppliedGeophysics, 50(1-2): 129-147, doi: 10.1016/S0926-9851(02)00135-0.

Weng A H, Wang X Q, Liu G X, et al. 2007. Nonlinear inversion of surface nuclear magnetic resonance over electrically conductive medium.ChineseJ.Geophys. (in Chinese), 50(3): 890-896, doi: 10.3321/j.issn:0001-5733.2007.03.030.

附中文参考文献陈斌, 胡祥云, 刘道涵等. 2014. 磁共振测深技术的发展历程与新进展. 地球物理学进展, 29(2): 650-659, doi: 10.6038/pg20140224. 戴苗, 胡祥云, 吴海波等. 2009. 地面核磁共振找水反演. 地球物理学报, 52(10): 2676-2682, doi: 10.3969/j.issn.0001-5733.2009.10.028.

李振宇, 潘玉玲, 张兵等. 2003. 利用核磁共振方法研究水文地质问题及应用实例. 水文地质工程地质, 30(4): 50-54, doi: 10.3969/j.issn.1000-3665.2003.04.011.

林君, 段清明, 王应吉等. 2011. 核磁共振找水仪原理与应用. 北京: 科学出版社. 林君, 蒋川东, 林婷婷等. 2013. 地下工程灾害水源的磁共振探测研究.地球物理学报, 56(11): 3619-3628, doi: 10.6038/cjg20131103. 林婷婷, 慧芳, 蒋川东等. 2013. 分层多指数磁共振弛豫信号反演方法研究. 地球物理学报, 56(8): 2849-2861, doi: 10.6038/cjg20130833.

潘玉玲, 张昌达. 2000. 地面核磁共振找水理论和方法. 武汉: 中国地质大学出版社.

潘玉玲, 李振宇, 万乐等. 2000. 利用核磁共振方法探查基岩裂隙水. CT理论与应用研究, 9(1): 22-25.

孙怀凤, 李貅, 李术才等. 2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演. 地球物理学报, 56(3): 1049-1064, doi: 10.6038/cjg20130333.

万乐, 潘玉玲. 1999. 利用核磁共振方法探查岩溶水. CT理论与应用研究, 8(3): 15-19.

万玲, 林婷婷, 林君等. 2013. 基于自适应遗传算法的MRS-TEM联合反演方法研究. 地球物理学报, 56(11): 3728-3740, doi:10.6038/cjg20131114.

王鹏. 2014. 均匀介质中MRS方法三维模型的核磁共振响应. CT理论与应用研究, 23(4): 569-578.

翁爱华, 王雪秋, 刘国兴等. 2007. 导电性影响的地面核磁共振反演. 地球物理学报, 50(3): 890-896, doi: 10.3321/j.issn:0001-5733.2007.03.030.

(本文编辑 何燕)

Three-dimensional joint interpretation of nuclear magnetic resonance and transient electromagnetic data

LI Xiu1, LIU Wen-Tao1, ZHI Qing-Quan2, ZHAO Wei1

1SchoolofGeologyEngineeringandGeomatics,Chang′anUniversity,Xi′an710054,China2InstituteofGeophysicalandGeochemicalExploration,ChineseAcademyofGeosciences,HebeiLangfang065000,China

The traditional interpretation methods of nuclear magnetic resonance (NMR) usually use 1D inversion based on homogeneous half space or layered conductive earth model and the information of water amount in each layer will be derived. However, these methods usually ignore the influence of the inhomogeneous underground conductivity to the interpretation results. Meanwhile, these results are easily restricted to local water-bearing structures. For the purpose of avoiding the problems aforementioned, a novel joint interpretation method combining transient electromagnetic (TEM) and NMR data is proposed in this paper, which provides an effective and practical interpretation method for the detection of complex hydrogeological conditions.This paper proposes a novel joint interpretation method combining transient electromagnetic (TEM) and NMR data based on the forward modeling theory of NMR method in 3D conductive media. Firstly, a fast resistivity image is derived from floating plate interpretation results of TEM data. Afterwards, the resistivity imaging data will be used as the electrical model in 3D NMR inversion. The distribution of transmitting magnetic field is calculated by FE method directly. The transmitting current source is loaded by introducing a pseudo-delta source, and the influence of “weak solution” in three dimensional simulation of magnetic field is eliminated by a force introduction of divergence condition. In order to improve the illness of sensitivity matrix and eliminate the noise, a non-linear fitting objective function considering the penalty terms is proposed and the linearized inversion method is used in the inversion process.The results of homogenous half-space model show that solutions of excitation magnetic field are almost the same as FEM solutions and digital filtering solutions and the influence of “weak solution” is eliminated. Results of the distribution of the NMR kernel function in different conductive models show that: (1) The background conductive of a model affects the distribution of the kernel function, especially when it is a low conductive one, and the lower of the conductive, the smaller range of the influence of excitation at the same pulse moment will be; (2) Local low resistive bodies with reasonably scale also have a significant effect on the distribution of the kernel function, lower resistivity and shallower buried depth causing greater influence, vice versa; Several conclusions can be drawn from the inversion results: (1) smaller variation of the geo-electrical model from the real case will lead to more accurate inversion results; (2) The inversion result can deviate from reality when using a homogenous half-space as the electrical model directly while the low conductive body have a certain scale, and the accuracy of the inversion result will see a significant improvement with the introduction of the floating plate interpretation method based on TEM data; (3) Though the accuracy of the floating plate interpretation decreases with increased depth, the impact of low conductive bodies on the distribution of the kernel function also decreases with that. Therefore, the fast resistivity image result based on TEM data, in spite of being an approximate result, can still offer a reasonable electrical model for NMR inversion.This paper proposes a novel joint interpretation method combining transient electromagnetic (TEM) and NMR data based on the forward modeling theory of NMR method in 3D conductive media. Results of the 3D distribution of kernel function show that low resistive bodies have a significant effect on the distribution of the kernel function, and the media conductivity should be considered during the NMR inversion. The floating plate interpretation based on TEM data can provide a reasonable geo-electrical model, and the accuracy of the NMR inversion will be improved significantly after introducing joint interpretation method combining transient electromagnetic (TEM) and NMR data.

Nuclear magnetic resonance; Transient electromagnetic; Equivalent conductive plane; 3D joint interpretation

国家重点基础研究发展计划项目(973项目)(2013CB036002)、国家重大科研设备研制项目(ZDYZ2012-1-05-04)和国家自然科学基金重点项目(51139004)联合资助.

李貅,男,1958年生,教授,博士生导师,主要从事瞬变电磁场的理论与应用方面的研究.E-mail:Lixiu@chd.edu.cn

10.6038/cjg20150810.

10.6038/cjg20150810

P631

2014-12-14，2015-07-08收修定稿

李貅， 刘文韬， 智庆全等. 2015. 核磁共振与瞬变电磁三维联合解释方法.地球物理学报，58(8):2730-2744,

Li X, Liu W T, Zhi Q Q, et al. 2015. Three-dimensional joint interpretation of nuclear magnetic resonance and transient electromagnetic data.ChineseJ.Geophys. (in Chinese),58(8):2730-2744,doi:10.6038/cjg20150810.