零售商部分延期支付下的动态库存和融资策略

温宗良，朱 雁，周优军

（1.广西中医药大学 药学院，广西 南宁 530001；2.徐州医学院 公共教育学院，江苏 徐州 221004；3.广西科技师范学院 数学与计算机科学系，广西 柳州 545004）

零售商部分延期支付下的动态库存和融资策略

温宗良1，朱 雁2，周优军3

（1.广西中医药大学 药学院，广西 南宁 530001；2.徐州医学院 公共教育学院，江苏 徐州 221004；3.广西科技师范学院 数学与计算机科学系，广西 柳州 545004）

在供应商允许零售商部分延期支付的条件下，讨论了风险中性的零售商周期性地订购一种产品以满足不确定性需求的随机动态库存决策问题，建立了优化补货和融资策略的库存模型，目的是最大化零售商计划期末的期望资金水平。零售商订货时可以使用自有资金和/或贷款资金，订货后如果有剩余资金，可通过无风险投资获得无风险收益。分析了给定初始资金和库存时的最优策略，并给出了数值实验。

零售商；动态库存；部分延期支付；订货策略；融资决策；随机需求

1 引言

交易信用是指企业间在产品交易中以延期付款的方式进行购销活动而形成的借贷关系，在实践中得到了广泛的应用。现实中的延期付款合同在执行时往往附带一些支付条件，如供应商要求零售商收到订货时支付部分货款[1]，如果提前期可以忽略不计，也就是要求订货时支付部分货款。供应商为了降低违约风险，允许信用等级高的顾客（或老顾客）完全延期支付，而信用等级低的顾客（或新顾客）只能部分延期支付。在现实商业交易中，由于交易双方财务状况、合作程度、谈判能力等的不同，这种供应商允许零售商在购买商品时只支付一定比例货款而延期支付剩余货款的交易行为广泛存在。比如丰田公司要求他的供应商提供完全的交易信用，但只向其下游经销商提供部分交易信用。

近年来，库存决策中的资金问题备受重视，其中部分延期支付既能刺激下游零售商订货，又能在一定程度上减少其违约的风险，在现实中得到了广泛使用，也引起了学者们的关注。Goyal[2]较早给出了存在延期付款时的EOQ模型，现有考虑部分延期和支付的文献大都在Goyal[2]的基础上放松某些假设进行推广。Huang[1]在Goyal[2]的基础上假定供应商允许零售商在订货量低于某一阈值时部分延期支付，建立了数学模型以确定最优订货周期和订货数量使得零售商的库存费用最小。Ouyang等[3]以及贾涛等[4,5]将Goyal[2]的模型扩展到易腐品。Taleizadeh等[6]则研究了部分延期支付、缺货部分补足的EOQ模型，分析了其最优订货量和缺货量。Zhou和Zhong[7]在EOQ模型的基础上，以零售商年平均费用最小为目标，建立了零售商在短信用期内可以部分付款并获得价格折扣、在长信用期内支付剩余部分货款的库存模型，给出了求解过程。张义刚和唐小我[8]在报童模型的框架下，建立了允许零售商部分延期付款预期利润模型，并用迭代算法确定了零售商不同保留利润下制造商的最优决策。

现有考虑库存和融资联合决策的文献大多研究单周期的问题，少有研究动态的多期问题。Archibald等[9]研究了最大化“自融资”初创企业长远生存率的最优策略。Chao等[10]研究了最大化“自融资”企业期望计划期末资产的最优策略。这两篇文献考虑利用内部资（和收入）的“自融资”，其他学者则考虑银行贷款、债券、增发股票等多种外部融资。Babich和Sobel[11]在固定利率短期债务的条件下，以最大化IPO预期折现所得为目标研究企业的运营和财务决策。Xu和Birge[12]假设企业可通过借款和发行股票获得资金，以最大化企业股东期望折现现金流为目标，立了有限计划期上的库存模型。Hu和Sobel[13]假设企业破产时支付违约惩罚后仍可运作，建立了与Xu和Birge[12]优化目标类似的模型研究企业的运营决策。Gong等[14]在Chao等[10]的基础上假定企业每周期都可以使用自有资金和/或短期借贷资金，以企业期望计划期末资产最大为目标，分析了企业的最优策略。

综上，现有关于部分交易信用的文献大多假设市场需求是确定的，在多周期部分延期支付条件下分析零售商的库存和融资联合决策的研究还未见发表。本文假设风险中性的零售商，在计划期内周期性地从供应商处订购一种产品以满足不确定性需求，订货时需要支付一定比例的货款，其余部分周期末支付，订货时可以使用自有资金和/或贷款资金，订货后如果有剩余资金，可以通过无风险投资获得无风险收益，建立了以计划期末的期望资金水平最大化为目标的随机动态决策模型，在分析模型性质的基础上，通过算例对模型进行了说明。

2 模型假设与记号说明

为了建立模型，引入如下记号与假设：

（1）将计划期分为N个相等的订货周期；第n(1≤n≤N)个周期的需求为Dn，其概率密度函数和分布函数分别为φ(·)和ϕ(·)，各周期的需求独立且同分布；

（2）补货率无限，提前期为零；允许缺货，缺货不补；本文的目标是最大化风险中性的零售商计划期末的期望资金水平，信誉损失并不影响问题的结构和性质，不考虑信誉损失；

（3）bn,xn,yn分别为第n(1≤n≤N)个周期决策前的资金水平和决策前后的库存水平，其中：-∞＜bn＜+∞, yn≥xn≥0;

（4）β为每次订货时立即支付货款的比例，0＜β≤1；

（5）c,p,s分别表示单位产品购买价格、零售价格和计划期末的残值，h为每个周期单位剩余产品的库存持有成本（不含资金成本），r,rf分别为每个周期内的贷款利率和无风险投资收益率，满足：-∞＜s≤c＜p，c(1+βr)＜p;

（6）假设供应商资金充足，零售商有一定的资产且信用良好（如有债务，会如期偿还）；

（7）a为实数，记a+=max{0,a}，a-=max{0,-a}。

3 模型建立

根据假设，零售商根据第n(1≤n≤N)期初的初始库存水平xn和资金水平bn决定订货后的库存水平为yn，即订货量为yn-xn，并立即支付β比例的货款 βc(yn-xn)，剩余部分在本期末支付。零售商如果资金充足，满足约束βc(yn-xn)≤bn，剩余资金将被进行无风险投资以获得无风险收益如果资金不足以支付这部分货款，零售商会通过向银行融资完成订单，并需在本期末偿还本息零售商在期末实现本期需求Dn，可获得收益需要支付库存费用(第N期末可获得残值如果零售商期末现金不足以偿还债务(包括延期支付的货款和贷款本息)，零售商将再次融资，此时资金水平为负。

因此，零售商在第n(1≤n≤N)期末，即第n+1期初的库存水平xn+1和资金水平bn+1分别为：

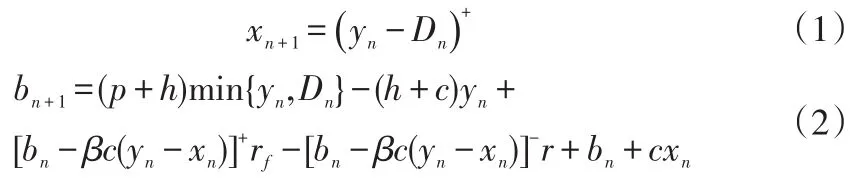
所以，零售商的决策问题是给定计划期初的库存水平x1和资金水平b1确定最优的订货策略，使计划期末的期望现金流最大，决策的优化问题为且需满足（1）、（2）两式及yn≥xn≥0。

记Vn(x,b)(1≤n≤N)为给定初始库存水平x和资金水平b的计划期末期望现金最大值，则最优性方程为：

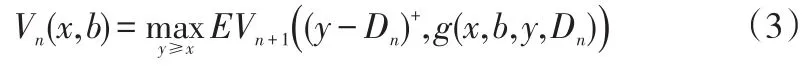
其中，

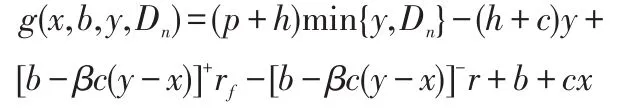
边界条件为：VN+1(x,b)=b+sx。

当β=1时，我们的模型即为Gong等[14]所构建的模型。

4 模型分析与求解

为了得到最优的订货策略，有：

引理1 对任意第n周期，固定x，则Vn(x,b)关于b递增。

引理1是很直观的：零售商期初的资金越多，计划期末的期望现金越多。

引理2 对于任意第n周期,固定A和B,则Vn(A-z,B+(p+h)z)关于z递增。

证明：对于任意第n周期，固定A和B，由式（3），得：

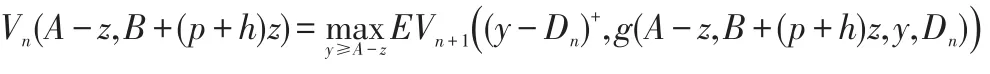
引理2表明在每周期初持有现金比库存更有利。因为通过订货可将现金转化为库存，反之不行，所以期初持有现金比库存更灵活。而持有库存太多且超过必需水平时，会失掉持有现金而获得无风险收益的机会。

定理1 对于任意第n周期，Vn(x,b)是关于(x,b)的凹函数。

证明：使用归纳法进行逆推。

显然，VN+1(x,b)=b+sx是关于 (x,b)的凹函数。假设Vn+1(x,b)是关于(x,b)的凹函数，下面证明Vn(x,b)是关于(x,b)的凹函数。

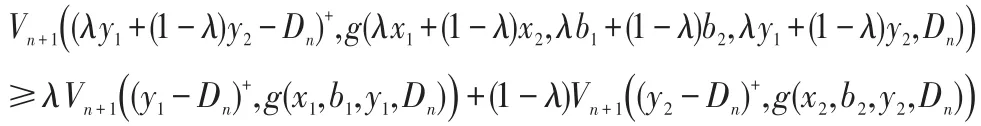
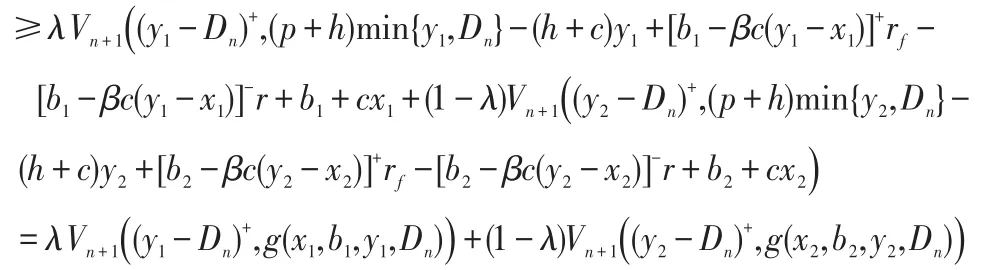
记R=x+b/(βc)表示零售商用尽自有资金但不贷款所能达到的订货后的库存水平，称之为“自有库存资产”。

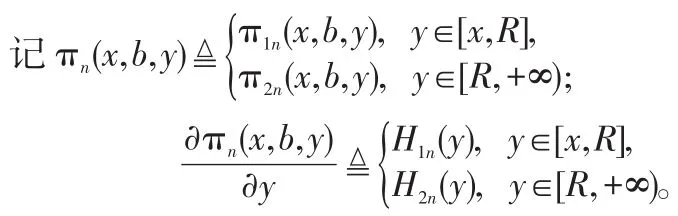
类似定理1的证明可得,对任意第n周期，给定(x,b), πn(x,b,y),π1n(x,b,y)和 π2n(x,b,y)都为关于 y的凹函数，且H1n(R)≥H2n(R)。记π1n(y),π2n(y)和πn(y)分别为给定(x,b)时π1n(x,b,y),π2n(x,b,y)和πn(x,b,y)的函数值。由πn(y)的连续性可知，π1n(R)=π2n(R)。记H1n(y)=0，H2n(y)=0的根分别为 y1n和y2n，由πn(y)的连续性及π1n(y)和π2n(y)的凹性，有：

引理3 若y1n＜R，则y2n＜R。

证明 反证法。假设y2n≥R则H2n(R)≥0。由y1n＜R知H1n(R)＜0，从而H2n(R)＞H1n(R)。这与H1n(R)≥H2n(R)矛盾。因此，若y1n＜R，则y2n＜R。证毕。

定理2 当第n期初状态为(x,b)且b＞0时，零售商的最优订货策略如下：

（1）若y1n≤x，则不订货；

（2）若x＜y1n≤R，则订至y1n;

（3）若y2n＜R≤y1n，则订至R;

（4）若R≤y1n且R≤y2n，则订至y2n。

证明 根据x与y1n,y2n的大小关系，分以下四种情形讨论：

情形1：y1n≤x且y2n≤x。

由y1n≤x知π1n(y)在区间[x,R]上单调递减，则对任意的y∈(x,R)，有π1n(R)≤π1n(y)＜π1n(x)，又由y2n≤x知π2n(y)在区间(R,+∞)上单调递减，则对任意的y∈(R,+∞)，有π2n(y)＜π2n(R)，而π1n(R)=π2n(R)，可得yˉ=x。

情形2：y1n＜x且y2n＞x。

由y1n＜x得y1n＜R及引理2知y2n＜R，此时π2n(y)在区间(R,+∞)上单调递减，则对任意的y∈(R,+∞)，π2n(y)＜π2n(R)。

由y1n＜x知π1n(y)在区间[x,R]上单调递减，则对任意的y∈(x,R]，有 π1n(R)≤π1n(y)＜π1n(x)，再由 π1n(R)=π2n(R)，得yˉ=x。

情形3：y1n＞x且y2n＜x。

显然有y2n＜R，从而π2n(y)在区间(R,+∞)上单调递减，则对任意的y∈(R,+∞)，π2n(y)＜π2n(R)。

当x＜y1n＜R时，由π1n(y)的凹性，知对任意的y∈[x,R]，π1n(y)≤π1n(y1n)，再由π1n(R)=π2n(R)，得yˉ=y1n。

当y1n≥R时，π1n(y)在区间[x,R]上单调递增，则对任意的y∈[x,R)，π1n(y)＜π1n(R)，再由π1n(R)=π2n(R)，得yˉ=R。

情形4：y1n＞x且y2n＞x。

当 x＜y1n＜R时，由引理2知 y2n＜R，此时π2n(y)在区间(R,+∞)上 单 调 递 减 ，则 对 任 意 的 y∈(R,+∞)，有π2n(y)＜π2n(R)。由 π1n(y)的凹性，知对任意的 y∈[x,R]，有π1n(y)≤π1n(y1n)，再由π1n(R)=π2n(R)，得yˉ=y1n。

当 y1n≥R 时，分 y2n＜R 和 y2n≥R 进行讨论。当y1n≥R＞y2n时，π1n(y)在区间[x,R]上单调递增，π2n(y)在区间(R,+∞)上单调递减，则对任意的y∈[x,R)，有π1n(y)＜π1n(R)，对任意的 y∈(R,+∞)，有 π2n(y)＜π2n(R)，由 π1n(R)=π2n(R)，得yˉ=R。当 y1n≥R且 y2n≥R时，π1n(y)在区间[x,R]上单调递增，则对任意的y∈[x,R)，有π1n(y)＜π1n(R)，又由π2n(y)的凹性，知 对 任 意 的 y∈[R,+∞)，有 π2n(y)≤π2n(y2n)，再 由π1n(R)=π2n(R)，得yˉ=y2n。

综上可知，若y1n≤x，则不订货；若x＜y1n＜R，则订至y1n；若y2n＜R≤y1n，则订至R；若R≤y1n且R≤y2n，则订至y2n，证毕。

定理3：当第n个周期期初状态为(x,b)且b≤0时，零售商的最优订货策略为：若y2n≤x，则不订货；否则，订到y2n。

从定理2可以看出，当第n期初资金水平为正时，库存系统存在两个订货的临界值y1n和y2n。当期初库存水平高于或等于临界值y1n时，最优策略为不订货，自有资金全部存入账户获得无风险利息，否则，最优策略取决于两个临界值和“自有库存资产”的大小关系。如果“自有库存资产”大于临界值y1n，则最优策略为订货到y1n，此种情形订货后仍有资金剩余，剩余资金存入账户获得无风险利息；如果“自有库存资产”介于两临界值之间，则最优策略为用尽自有资金，此时没有剩余资金，也无需融资；如果“自有库存资产”不超过两临界值，则最优策略为订货到y2n，此时自有资金不足以使订货达到y2n，零售商需要通过融资来完成订货。

从定理3可以看出，当第n期初资金水平为非正时，库存系统的订货策略相对简单，只有一个订货的临界值y2n，此时库存策略只依赖于期初库存水平和此临界值的大小关系。当期初库存水平高于或等于临界值y2n时，最优策略为不订货；否则最优策略为订货到y2n，此时，零售商需要通过融资来完成订货。

5 数值实验

设计划期分为4个订货周期，零售商每周期初的采购价格c=2，零售价格p=2.5，计划期末的残值s=1，订货时立即支付货款的比例β=0.85，每周期单位剩余产品的库存持有成本h=0.1，每个周期内的贷款利率和无风险利率分别为r=0.2和rf=0.05。每个周期的需求都为独立同分布的截尾正态分布，均值和标准差分别为4和1.5。表1列出了零售商各周期（部分）给定初始状态的最优订货策略。表中第二行表示每周期初的库存水平，第一列表示每周期初的资金水平，表格中数据为行列交叉所表示状态的最优订货策略（订货后达到的库存水平）。3.03。由表1可以看出，对于第4周期策略结构比较简单，存在两个临界值，给定期初状态的最优策略取决于状态与临界值的关系；而对于其他各周期（此处以第3周期为例），由于模型本身的复杂性导致策略结构比较复杂，存在着某些区域，当给定初始库存（资金）而拥有更多的资金（库存）时，订货后达到的库存水平反而会减少，这与第4周期所具有的给定初始库存（资金）时资金（库存）增加则订货后达到的库存水平不减这一性质不同，文献[14]中的模型也有类似的性质。这种反直观的现象来源于多余资金的投资价值。

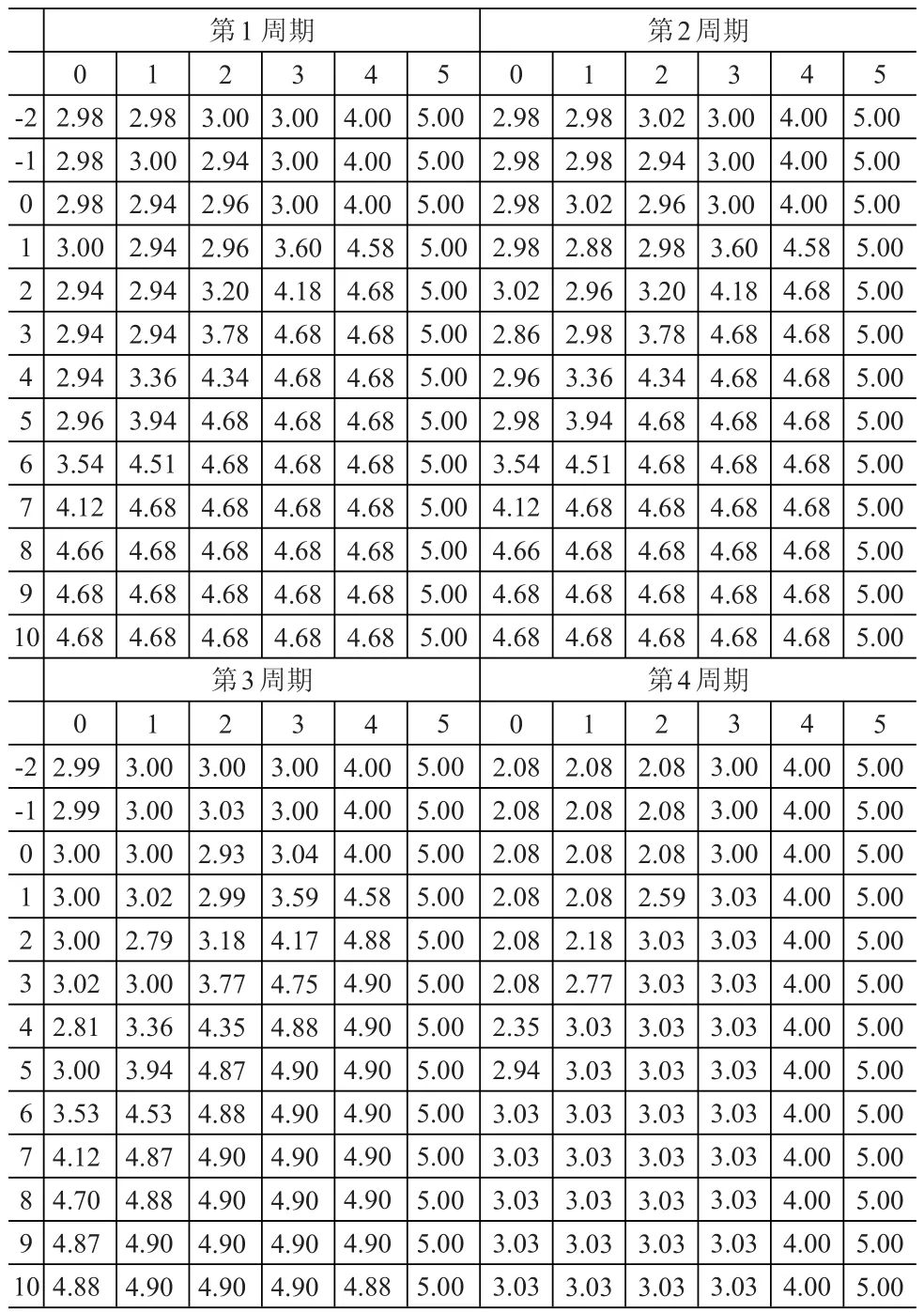
表1 零售商各周期给出初始状态的最优订货策略

6 结论

在现实中，由于交易双方财务状况、合作程度、谈判能力等的不同，部分延期支付广泛存在于交易实践中。本文从实际出发，假设风险中性的零售商存在资金约束，在供应商允许部分延期支付的条件下周期性地订购一种产品以满足不确定性需求，订货时可以使用自有资金和（或）贷款资金，订货后如果有剩余资金，可以通过无风险投资获得无风险收益，以最大化计划期末的期望资金水平为目标，建立了随机动态模型。在分析模型性质的基础上，通过算例对模型进行了说明。本文的研究对于市场需求不确定下实施部分信用交易的订货和融资联合决策具有一定的理论价值。进一步的研究方向，可以考虑零售商的风险偏好、存在破产风险等情形。

[1]Huang Y F.Economic order quantity under conditionally permissible delay in payments[J].European Journal of Operational Research,2007, 176(2):911-924.

[2]Goyal S K.Economic order quantity under conditions of permissible delay in payments[J].Journal of the Operational Research Society,1985, 36:335-338.

[3]Ouyang L Y,Teng J T,Goyal S K,et al.An economic order quantity model for deteriorating items with partially permissible delay in payments linked to order quantity[J].European Journal of Operational Research,2009,194(2):418-431.

[4]贾涛,徐渝,耿凯平.部分延期付款下易腐品联合经济订货批量模型究[J].运筹与管理,2011,20(8):1-9.

[5]贾涛,郑毅,徐渝,等.顾客部分延期付款下两级商业信用易腐品订货策略[J].运筹与管理,2013,22(2):150-158.

[6]Taleizadeh A A,David W P,Mohammad S J,et al.An EOQ model with partial delayed payment and partial backordering[J].Omega,2013,41(2): 354-368.

[7]Zhou Y W,Zhong Y G.How to make the replenishment and payment strategy under flexible two-part trade credit[J].Computers&Operations Research,2013,40(5):1 328-1 338.

[8]张义刚,唐小我.部分延期付款下的制造商决策与供应链协调[J].管理学报,2012,9(10):1 536-1 547.

[9]Archibald T,Thomas L,Betts J,et al.Should start-up companies be cautious?Inventory policies which maximize survival probabilities[J].Management Science,2002,48(9):1 161-1 174.

[10]Chao X,Chen J,Wang S.Dynamic inventory management with cash flow constraints[J].Naval Research Logistics,2008,55(8):758-768.

[11]Babich V,Sobel M J.Pre-IPO operational and financial decisions[J]. Management Science,2004,50(7):935-948.

[12]Xu X,Birge J R.Equity valuation,production,and financial planning: A stochastic programming approach[J].Naval Research Logistics,2006, 53(7):641-655.

[13]Hu Q,Sobel M J.Echelon base-stock policies are financially sub-optimal[J].Operations Research Letters,2007,35(5):561-566.

[14]Gong X,Chao X,Simmchi D.Dynamic inventory control with limited capital and short-term financing[J].Naval Research Logistics,2014,61 (3):184-201.

[15]Heyman D P,Sobel M J.Stochastic models in operations research:stochastic optimizations[M].Courier Dover Publications,2003.

Study on Dynamic Inventory and Financing Strategy with Partial Delay in Payment by Retailer Allowed

Wen Zongliang1,Zhu Yan2,Zhou Youjun3
(1.School of Pharmacy,Guangxi University of Chinese Medicine,Nanning 530001; 2.School of Public Education,Xuzhou Medical College,Xuzhou 221004; 3.School of Mathematics&Computer Science,Guangxi Normal College of Science&Technology,Liuzhou 545004,China)

In this paper,upon the premise that the supplier allows the partial delay in payment of the retailer,we discussed the stochastic dynamic inventory decision-making problem of a risk-neutral retailer that made cyclic ordering of a product to meet the uncertain demand for it,built the inventory model that optimized its replenishment and financing strategies so as to maximize the expected fund level of the retailer at the end of a term,and at the end,presented a numerical example to analyze the optimal initial investment and the optimal inventory level.

retailer;dynamic inventory;partial delay in payment;ordering strategy;financing decision-making;stochastic demand

F715.6；O141.4

A

1005-152X(2015)11-0067-05

10.3969/j.issn.1005-152X.2015.11.020

2015-10-02

国家自然科学基金项目（71261002）；广西高校科学技术研究项目（KY2015YB366）；广西中医药大学项目（QN14006）

温宗良（1981-），男，山东聊城人，博士研究生，讲师，研究方向：库存控制、供应链金融；朱雁（1983-），女，安徽萧县人，讲师，研究方向：优化与管理；周优军(1974-)，通讯作者，男，广西全州人，硕士，副教授，研究方向:物流与供应链管理。