基于光滑粒子流体动力学法单颗磨粒超声辅助磨削陶瓷材料的磨削力仿真研究

米召阳，梁志强，王西彬，周天丰，赵文祥，田梦

(北京理工大学先进加工技术国防重点学科实验室，北京100081)

0 引言

近年来，随着科技的发展，SiC 陶瓷、Al2O3陶瓷、玻璃、蓝宝石等硬脆性材料因其硬度高、耐磨损、抗腐蚀、化学性能稳定，被广泛应用于机械、电子、医疗、化工、光学、航空航天、国防军工等领域［1-3］，然而这些材料往往脆性很大，加工过程中会在工件表面/亚表面形成微裂纹，从而影响工件的使用性能。磨削是目前应用最为广泛的精密加工工艺之一。为了提高加工效率、提高被加工件表面质量，磨削通常用在零件加工的最后一道工序。传统磨削过程中会产生大量的磨削热及较大的磨削力，从而引起工件表面/亚表面损伤、降低被加工件的使用性能、降低砂轮寿命等问题［4］。为了解决这些问题，超声振动被引入到磨削中，国内外广泛的研究证实超声辅助磨削在降低磨削力、提高工件表面加工质量、降低工件表面损伤等方面有着显著的优势［5-7］。

通常对磨削机理的研究是通过实际磨削实验来完成的。实际磨削实验成本高、实验条件要求复杂，因此存在着许多困难。目前，已有很多学者利用有限元仿真的方法对磨削机理进行研究。基于网格划分的有限元仿真在模拟磨削过程中会遇到以下难题:网格由于产生大变形畸变而终止计算、切屑分离准则较难准确定义、刀具与工件之间的摩擦较难处理等［8］。近年来，在切削仿真领域发展起来一种相对新型的数值计算方法，即光滑粒子流体动力学(SPH)法，SPH 法是一种纯拉格朗日无网格算法，由Lucy、Gingold 和Monaghan 开发得到，克服了网格划分法由于产生大变形畸变而终止计算这一难题［9-11］。该方法利用大量具有一定质量的粒子来离散计算域，粒子本身就代表材料，因此通过粒子的运动状态便可以反映出被加工材料的状态［12］。Guo等［13］利用SPH 法模拟车削K9 玻璃的过程，得到K9 玻璃的临界切削深度和不同前角下的车削力以及前角对临界切削深度的影响。Limido 等［14］利用SPH 法仿真车削AISI4340 钢的过程，证明基于SPH法的车削仿真能够准确预测连续切屑的形成过程，并且在不引入修正系数的情况下准确预测切削力。徐世龙等［8］利用SPH 法对磨削机理进行仿真，发现基于SPH 法的磨削仿真能够很好地解释磨削过程中工件材料的弹塑性变形行为和切屑的形成情况，且证明了磨削过程中存在着一个切屑产生的临界磨削深度。宿崇等［15］利用SPH 法进行陶瓷立方氮化硼(CBN)砂轮地貌模型磨削仿真，通过切削层SPH粒子的运动情况，分析了磨粒的切削机理及工件表面的创成机理。SPH 法在研究超声辅助磨削硬脆性材料时能够很好地反映仿真中材料受到冲击而破坏的情况及磨粒的受力，能有效地揭示硬脆性材料的磨削机理。

本文利用SPH 法分别对单颗磨粒超声辅助磨削SiC 陶瓷、Al2O3陶瓷的过程进行仿真，通过分析轴向超声振动对磨削中平均未变形切屑厚度的影响，揭示轴向超声振动对磨削SiC 陶瓷、Al2O3陶瓷的磨削力影响机制。

1 轴向超声辅助磨削系统原理

轴向超声辅助磨削的原理如图1所示，在普通磨削的基础上对砂轮或工件施以轴向的超声振动，磨削过程中，砂轮的磨削深度为ap，工作台以速度vw作进给运动，同时砂轮以线速度vs旋转。

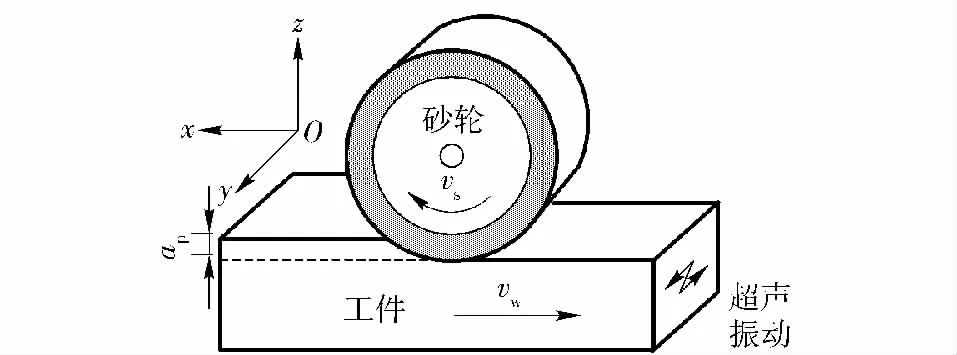
图1 超声磨削原理示意图Fig.1 Processing principle of UAG

磨削是磨粒与工件相互干涉去除材料的过程，因此，研究磨粒与工件之间的相对运动对研究材料去除机理有重要作用。磨削中有无超声作用下单颗磨粒相对于工件的运动轨迹如图2所示。在轴向超声辅助磨削中，由于超声振动的作用，磨粒在工件上的轨迹为一个正弦曲线，不同磨粒的路径相互干涉，使磨粒刻划的沟槽尺寸变宽、变浅，能够减小磨粒的受力，另外由于磨粒的冲击作用，减小了材料的塑性变形，能够降低磨削热，同时磨粒的冲击作用还能促进磨屑与工件基体分离，提高材料去除率。

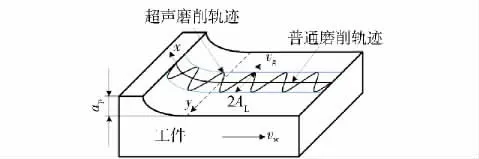
图2 单颗磨粒的加工运动模型Fig.2 Motion trajectory of abrasive grain on workpiece

为了研究磨粒与工件之间的相对运动，在砂轮与工件的接触面上建立Oxy 坐标系，如图2所示，得到轴向超声辅助磨削中单颗磨粒相对于工件的运动轨迹［16］:

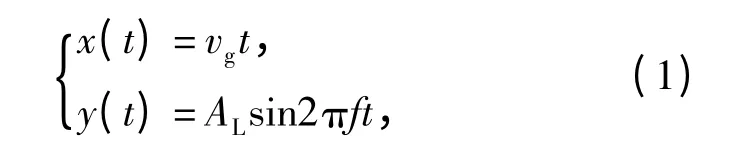
式中:vg为砂轮圆周方向磨粒相对于工件的线速度;AL为超声振动振幅;f 为超声振动频率。

单颗磨粒相对于工件的运动速度

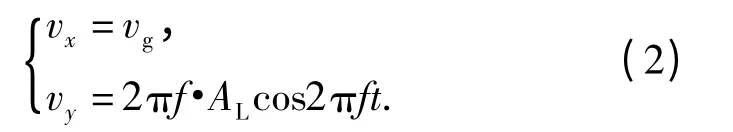
在轴向超声磨削磨粒速度vg=1 m/s，超声振动频率f=50 kHz(周期T=20 μs)，振幅AL=3 μm 时，接触平面内磨粒的位移、速度随时间变化规律如图3所示，由于超声振动的作用，磨粒的位移发生周期性变化，而速度同样发生周期性变化，位移、速度的变化规律相差π/2 相位。

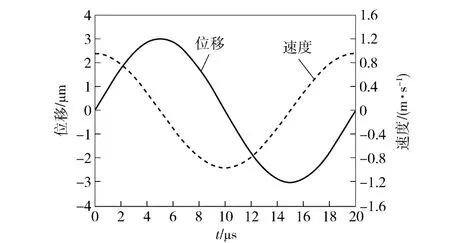
图3 磨削平面内磨粒的运动特性Fig.3 Kinematic characteristics of abrasive in UAG

2 超声辅助磨削中平均未变形切屑厚度分析

在轴向超声辅助磨削中，接触平面内单颗磨粒的切削轨迹是一个正弦曲线，而在普通磨削中磨粒的切削轨迹为一条单向弧线，如图2中所示。在普通磨削中，单颗磨粒在砂轮旋转一个周期内的切削轨迹长度［17］为

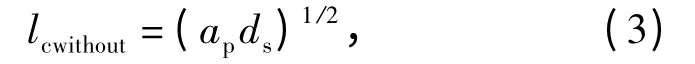
式中:ds为砂轮的直径。

根据(1)式得到，轴向超声辅助磨削中，单颗磨粒的轨迹为

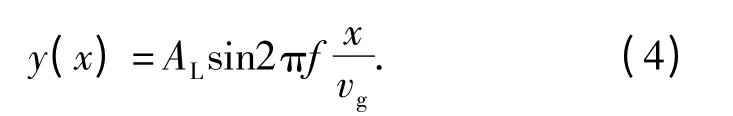
由(3)式、(4)式得到，轴向超声辅助磨削中，单颗磨粒在砂轮旋转一个周期内的切削轨迹长度为

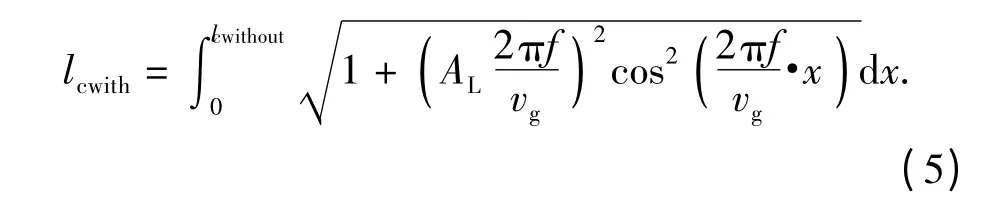
磨削中，砂轮的动态有效磨粒数为N = Cebvs，其中Ce为砂轮表面上单位面积有效磨粒数，b 为砂轮磨削宽度。单位时间内材料的去除体积V 取决于砂轮深度ap、砂轮磨削宽度b 与工件进给速度vw，得到V =apvwb. 单位时间内产生的切屑数和每一切屑体积的乘积等于体积去除率，即［17］

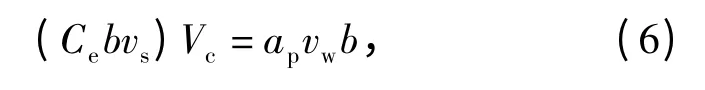
式中:Vc为单个切屑的体积。

由于最大未变形切屑厚度hm≪切屑长度lc［17］，未变形切屑可以近似为一个三菱锥，截面为三角形，如图4所示。假设r 是切削路径任一点处切屑宽度bc与厚度h 的比，即r =bc/h，而磨屑的体积为最大截面积(rh2m/2)和长度lc乘积的1/3，即［17］

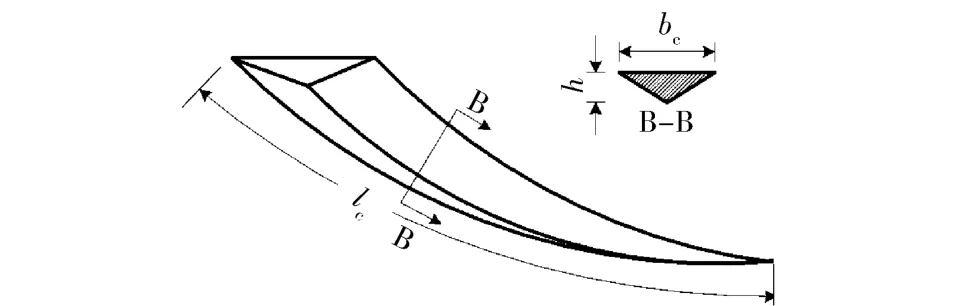
图4 未变形切屑模型Fig.4 Undeformed chip model in grinding

把(7)式带入(6)式得到最大未变形切屑厚度的表达式［17］:

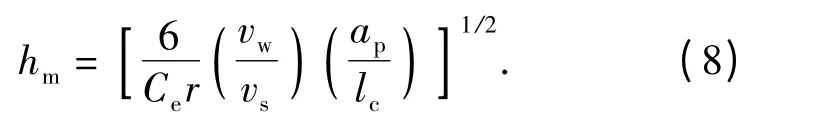
磨削中的平均未变形切屑厚度为ha，单个磨屑的体积为磨屑的平均截面积(rh2a/2)和长度lc的乘积，即

根据(7)式、(9)式得到，磨削中平均未变形切屑厚度与最大未变形切屑厚度之间的关系:

根据(8)式、(10)式得到，磨削中平均未变形切屑厚度的表达式:

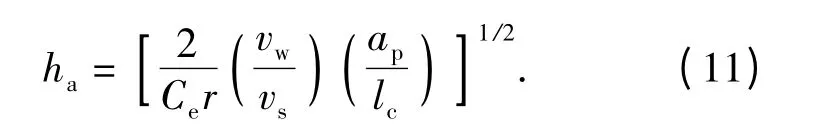
根据(11)式，有无超声作用时平均未变形切屑厚度与磨粒的切削轨迹长度呈如下比例关系:

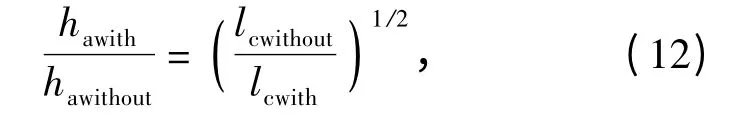
式中:hawith与hawithout分别为有无超声作用时的平均未变形切屑厚度。

把(3)式、(5)式带入到(12)式中得到

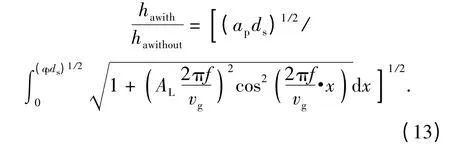
根据(12)式与(13)式，轴向超声的施加，促使超声磨削的磨粒切削轨迹长度明显大于普通磨削，从而导致超声辅助磨削的平均未变形切屑厚度小于普通磨削。由于磨削力与平均未变形切屑厚度呈一定比率关系，超声磨削过程中未变形切屑厚度减小是磨削力降低的重要原因［18］。

为了验证有无超声振动磨削的切屑厚度关系，在一定的磨削参数下，计算了有无超声磨削的平均未变形切屑厚度比值hawith/hawithout，所得结果如图5所示。从图中可以看出，轴向超声磨削的平均未变形切屑厚度hawith小于普通磨削hawithout. 而且在一定磨削速度下，平均未变形切屑厚度的比值随着超声振动振幅的增加而减小。当振幅不变时比值随着磨削速度的减小而降低。这说明增加超声振动振幅、减小磨削速度，能够进一步减小超声磨削中的平均未变形切屑厚度，从而有效降低磨削力。

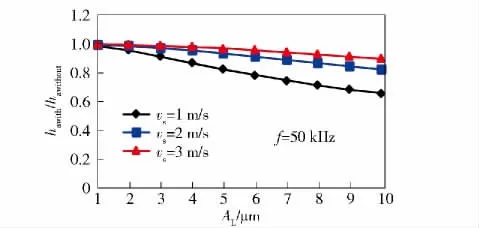
图5 磨削速度与超声振幅对切屑厚度比值hawith/hawithout的影响规律Fig.5 hawith/hawithout ratio vs. cutting speed and vibration amplitude

3 单颗磨粒超声辅助磨削陶瓷仿真条件及仿真模型的建立

基于得到的平均未变形切屑厚度比值hawith/hawithout随超声振动振幅、磨削速度变化而变化的规律，可以进一步推断超声振动磨削力的变化规律。利用SPH 法分别对单颗磨粒超声辅助磨削SiC陶瓷、Al2O3陶瓷的磨削力进行仿真实验验证。仿真中，利用拉格朗日网格对磨粒建模，利用SPH 法对工件建模。磨粒的材料选用金刚石，由于金刚石材料的硬度大于工件材料，因此定义磨粒为刚体。工件材料分别选择SiC 陶瓷、Al2O3陶瓷。本构模型选择JH-2 模型，SiC 陶瓷与Al2O3陶瓷的JH-2 模型参数在表1［19］中给出，其中:A 为初始强度参数;B为断裂强度系数;C 为应变率系数;M 为断裂强度指数;N 为初始强度指数。单颗磨粒磨削陶瓷的SPH模型如图6所示。

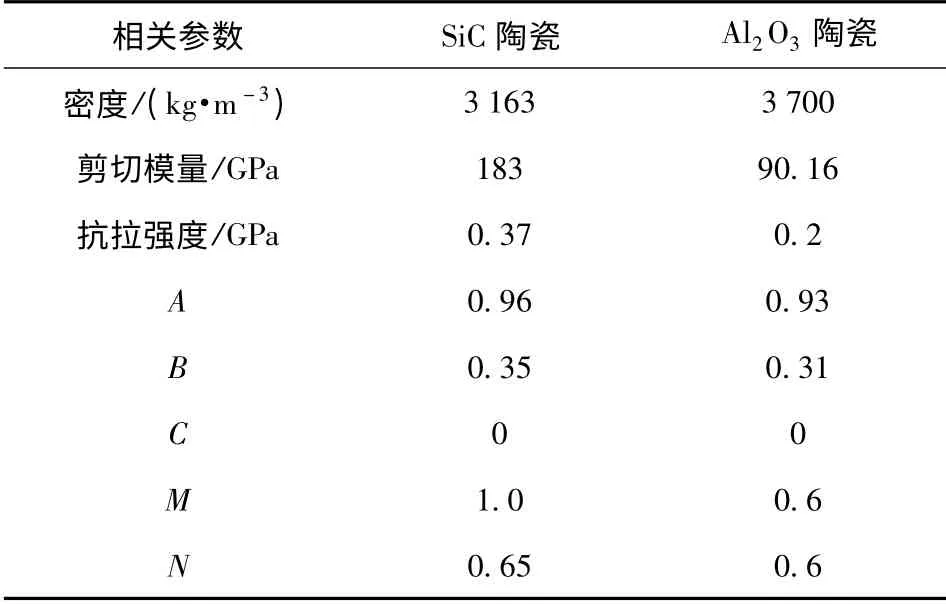
表1 SiC 陶瓷与Al2O3 陶瓷JH-2 模型材料参数Tab.1 Constitutive parameters of SiC and Al2O3 ceramics

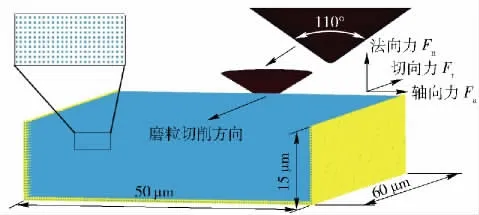
图6 单颗磨粒磨削SiC 陶瓷、Al2O3 陶瓷仿真SPH 模型Fig.6 SPH grinding model for single diamond abrasive grain to grand SiCand Al2O3 ceramics

假设磨粒速度vg为1 m/s，普通磨削平均未变形切屑厚度为1.5 μm，超声磨削的频率定为50 kHz，振幅分别为2 μm、3 μm、4 μm，对应的平均未变形切屑厚度由(12)式计算得到，结果在表2中给出。磨削仿真的其他条件参数也在表2中给出，仿真中磨粒的切深为实际磨削中的平均未变形切屑厚度ha.仿真中的接触类型为CONTACT_ NODES_ TO_SURFACE.

4 仿真结果及分析

单颗磨粒轴向超声磨削(f=50 kHz、AL=3 μm)与普通磨削的仿真结果如图7所示。从图7(a)中可以看出，在轴向超声振动的作用下磨粒的切削路径为一个正弦曲线。图7(b)中所示，普通磨削磨粒的切削路径为一条直线。在图7(a)中，切屑随着磨粒的切削路径，以较分散的形式分离出去。这主要是由于超声磨削时磨粒的切削速度、加速度方向都是随着时间而不断周期变化的，即磨粒在向前切削的过程中不断的左右摆动，导致切屑的飞出方向不断改变。与之相比，在图7(b)中，普通磨削时，磨粒以单一方向进行切削，切屑主要从磨粒的前方和两侧飞出，因此切屑以较为集中的形式分离出去。因此，在超声振动磨削中，磨屑分散有利于切屑与工件的分离，避免了普通磨削中容易产生的切屑堵塞砂轮等问题。图8所示为单颗磨粒磨削SiC 陶瓷时磨粒受到的磨削力。图9所示为单颗磨粒磨削Al2O3

陶瓷时磨粒受到的磨削力。分别对比图8(a)、图8(b)与图9(a)、图9(b)，得到超声磨削中单颗磨粒受到的法向力、切向力均小于普通磨削中磨粒的受力。从图8(a)、图9(a)中可以看出，由于轴向振动的作用，会引入一个周期变化的轴向力，该力有利于切屑与工件的分离，提高了磨削中的材料去除率。

表2 磨削参数Tab.2 Grinding parameters

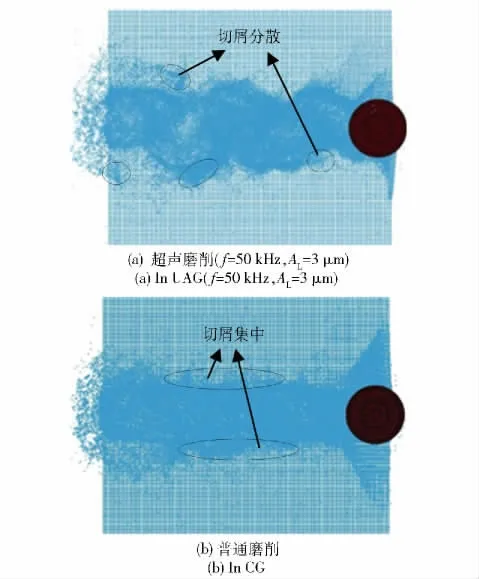
图7 磨削仿真中的材料变形情况Fig.7 The chip deformation in UAG and CG

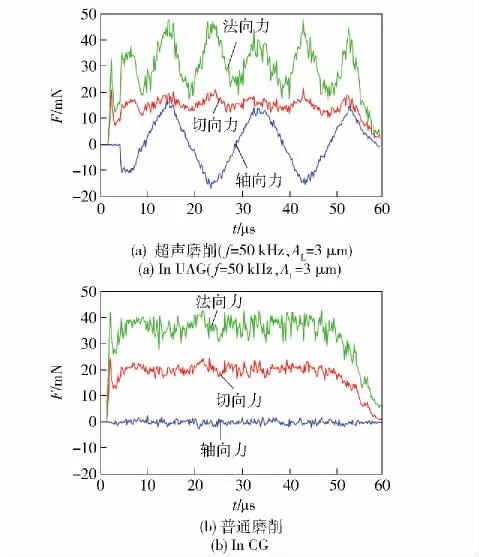
图8 磨削SiC 陶瓷时单颗磨粒磨削力Fig.8 The simulated grinding forces in the grinding of SiC ceramics

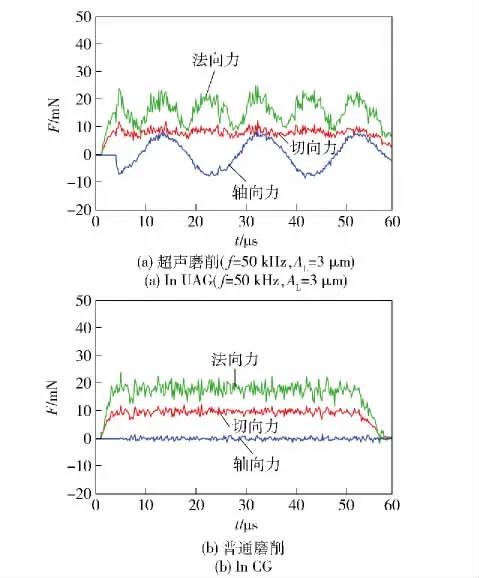
图9 磨削Al2O3 陶瓷时单颗磨粒磨削力Fig.9 The simulated grinding forces in the grinding of Al2O3 ceramics

提取不同振幅条件下磨粒受力的仿真数据并计算一个周期内的平均值，结果如图10 所示。从图10 中可以看出，单颗磨粒磨削两种材料时，不同情况下磨粒受到的切向力均比法向力小，轴向力接近于0. 随着振幅的增加，磨粒受到的法向力、切向力逐渐降低。分别对比图8(a)与图9(a)，图8(b)与图9(b)、图10(a)与图10(b)发现，在相同磨削条件下，单颗磨粒在磨削SiC 陶瓷时受到的磨削力大于磨削Al2O3陶瓷时的磨削力。这是因为SiC 陶瓷的剪切模量、抗拉强度与硬度均大于Al2O3陶瓷，因此在磨粒与工件相互作用去除材料的过程中，磨削SiC 陶瓷材料时磨粒受到的磨削力大。由于SiC陶瓷的屈服强度大于Al2O3陶瓷的屈服强度，磨削中去除等量体积材料时SiC 陶瓷消耗的磨削能大于Al2O3陶瓷消耗的磨削能，从而导致磨粒在磨削SiC陶瓷时受到的磨削力大于在磨削Al2O3陶瓷时的磨削力。

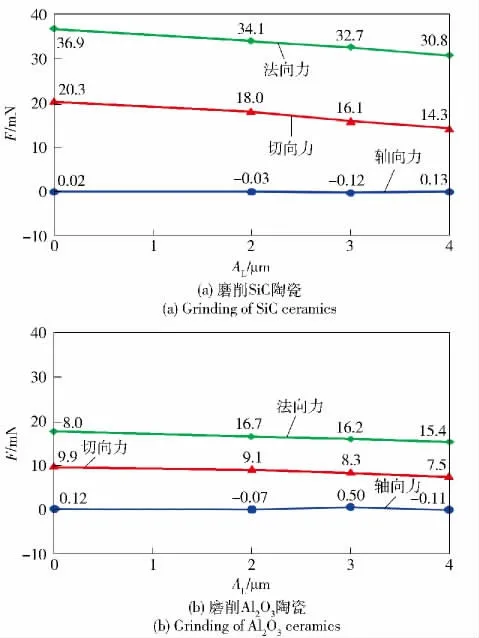
图10 不同振幅时单颗磨粒的平均磨削力(vs =1 μm/μs，f=50 kHz)Fig.10 Relationship between grinding forces and vibration amplitude (vs =1 μm/μs，f=50 kHz)

磨削两种材料时不同超声振幅条件下磨粒受到的法向力、切向力相对于普通磨削时的降低比率如图11 所示。从图11 中可以看出，随着轴向振幅的增加，与磨削法向力相比，磨削切向力降低幅度更大。这表明在较大的超声振幅作用下能够有效减小磨削能消耗，从而降低磨削热量，减小磨削表层热损伤。

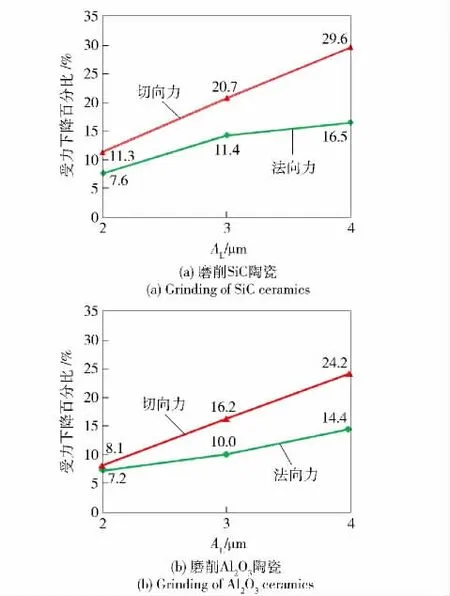
图11 超声磨削仿真中单颗磨粒磨削力下降比率Fig.11 The force decrease ratio in UAG simulation

5 结论

本文建立了一种轴向超声辅助磨削平均未变形切屑厚度数学模型，并基于该模型分析了磨削速度、超声振幅对磨削过程中平均未变形切屑厚度的影响规律。利用SPH 法在不同超声振幅条件下对单颗磨粒超声辅助磨削SiC 陶瓷、Al2O3陶瓷磨粒所受磨削力进行仿真实验，结论如下:

1)与普通磨削的平均未变形切屑厚度相比，超声辅助磨削的切屑厚度较小，而且随着轴向超声振幅的增加，平均未变形切屑厚度进一步降低，随着磨削速度的增加，切屑厚度减小比例降低。

2)单颗磨粒超声辅助磨削SiC 陶瓷、Al2O3陶瓷的磨削力变化规律与平均未变形切屑厚度的变化一致。超声磨削过程的磨削力小于普通磨削，而且随着超声振幅的增加，磨削力显著减小。

3)相同磨削条件下，磨削SiC 陶瓷时的磨削力大于磨削Al2O3陶瓷时的磨削力。

4)超声辅助磨削中，随着超声振幅的增加，磨削切向力降低幅度大于磨削法向力。在较大的超声振幅作用下能够有效减小磨削能消耗，减小磨削表层热损伤。

References)

［1］Ishihara M，Baba S，Takahashi T，et al. Fundamental thermo mechanical properties of SiC-based structural ceramics subjected to high energy particle irradiations［J］. Fusion Engineering and Design，2000，51/52:117 -121.

［2］陈维平，韩孟岩，杨少锋.Al2O3陶瓷复合材料的研究进展［J］.材料工程，2011，21(3):91 -96.CHEN Wei-ping，HAN Meng-yan，YANG Shao-feng. Research progress of Al2O3ceramic composites［J］. Journal of Materials Engineering，2011，21(3):91 -96. (in Chinese)

［3］Saito T，Kawamoto H，Yamamoto T，et al. Lattice strain and dislocations in polished surfaces on sapphire［J］. Journal of the American Ceramic Society，2005，88(8):2277 -2285.

［4］周志雄，毛聪，周德旺，等.平面磨削温度及其对表面质量影响的实验研究［J］.中国机械工程，2008，19(8):980 -984.ZHOU Zhi-xiong，MAO Cong，ZHOU De-wang，et al. Experimental investigation of grinding temperature and its effects on surface quality in surface grinding［J］. China Mechanical Engineering，2008，19(8):980 -984. (in Chinese)

［5］Liang Z，Wu Y，Wang X，et al. A new two-dimensional ultrasonic assisted grinding (2D-UAG)method and its fundamental performance in monocrystal silicon machining［J］. International Journal of Machine Tools and Manufacture，2010，50(8):728 -736.

［6］Tawakoli T，Azarhoushang B，Mohammad R. Ultrasonic assisted dry grinding of 42CrMo4 ［J］. The International Journal of Advanced Manufacturing Technology，2009，42(9/10):883 -891.

［7］Uhlmann E，Spur G. Surface formation in creep feed grinding of advanced ceramics with and without ultrasonic assistance ［J］.CIRP Annals-Manufacturing Technology，1998，47(1):249 -252.

［8］徐世龙，林建忠，杨玉廷.基于SPH 方法的磨削机理仿真研究［J］.制造技术与机床，2012(12):136 -139.XU Shi-long，LIN Jian-zhong，YANG Yu-ting. Simulation study of grinding mechanism based on SPH［J］. Manufacturing Technology＆ Machine Tool，2012(12):136 -139. (in Chinese)

［9］Lucy L. A numerical approach to the testing of the fission hypothesis［J］. Astronomical Journal，1977，82(12):1013 -1024.

［10］Gingold R，Monaghan J. Smoothed particle hydrodynamics:theory and application to non-spherical stars［J］. Monthly Notices of the Royal Astronomical Society，1977，181(3):375 -389.

［11］Monaghan J. An introduction to SPH ［J］. Computer Physics Communications，1988，48(1):89 -96.

［12］Li W，Yin S，Wang X. Numerical investigations of the effect of oblique impact on particle deformation in cold spraying by the SPH method ［J］. Applied Surface Science，2010，256(12):3725 -3734.

［13］Guo X，Wei Y，Jin J，et al. A numerical model for optical glass cutting based on SPH method［J］. The International Journal of Advanced Manufacturing Technology，2013，68 (5/6/7/8):1277 -1283.

［14］Limido J，Espinosa C，Salaun M，et al. SPH method applied to high speed cutting modelling［J］. International Journal of Mechanical Sciences，2007，49(7):898 -908.

［15］宿崇，施志辉，刘元伟.陶瓷CBN 砂轮地貌建模与磨削仿真［J］.中国机械工程，2012，23(14):1742 -1745.SU Chong，SHI Zhi-hui，LIU Yuan-wei. Topography modeling and grinding simulation of vitrified bonded CBN wheel［J］. China Mechanical Engineering，2012，23(14):1742 - 1745. (in Chinese)

［16］Wu Y，Nomura M，Feng Z，et al. Modeling of grinding force in constant-depth-of-cut ultrasonically assisted grinding［J］. Materials Science Forum，2004，471/472:101 -106.

［17］Malkin S. Grinding technology:theory and applications of machining with abrasives［M］. Los Angeles，US:Society of Manufacturing Engineers，1989:35 -45.

［18］任敬心，康仁科，史兴宽. 难加工材料的磨削［M］. 北京:国防工业出版社，1999:20 -22.REN Jing-xin，KANG Ren-ke，SHI Xing-kuan. Grinding of difficult-to-cut materials［M］. Beijing:National Defense Industry Press，1999:20 -22. (in Chinese)

［19］Cronin D，Bui K，Kaufmann C，et al. Implementation and validation of the Johnson-Holmquist ceramic material model in LS-Dyna［C］∥4th European LS-DYNA Users Conference. Ulm，Germany:ARUP，2003.