仅含两个稳定平衡点的4D分数阶系统的动力学与同步

吴然超，赵玉晗

(安徽大学 数学科学学院，安徽 合肥 230039)



仅含两个稳定平衡点的4D分数阶系统的动力学与同步

吴然超，赵玉晗

(安徽大学 数学科学学院，安徽 合肥 230039)

[摘要]本文构造了一个新的四维分数阶混沌系统，与至少含有一个不稳定平衡点的一般分数阶混沌系统不同的是，该系统仅有两个稳定平衡点。首先给出了两个平衡点局部渐近稳定的充分条件，通过数值模拟验证了该系统的混沌吸引子与两个稳定平衡点共存。然后，基于分数阶Lyapunov稳定性理论，在误差系统保留非线性项的情况下，利用反馈控制实现了此系统的同步，数值模拟进一步证实了结论的正确性。

[关键词]分数阶系统；稳定性；混沌；同步

分数阶混沌系统是整数阶混沌系统的推广，相比之下更能描述系统的动力学行为，在物理学和工程学等领域有着广泛的应用[1]。近年来，分数阶混沌系统引起了人们广泛的兴趣，随着研究的深入，构造了许多分数阶混沌系统，例如,分数阶Lorenz系统,分数阶Rssler系统，分数阶Chen系统和分数阶统一系统及其推广形式等。

注意到在这些分数阶混沌系统中，一般都至少含有一个不稳定平衡点。然而，与这些系统不同，本文根据整数阶广义Sprott C系统[2]，构造了一个新的四维分数阶混沌系统，该系统仅有两个稳定平衡点，并且同时能够产生混沌吸引子。本文主要探讨该特殊系统的一些混沌性态，并实现该混沌系统的同步。

由于混沌系统对初值的敏感性和时间上的不可预测性，混沌的同步成为了混沌应用的重要环节，在数字信号、密码安全等方面有着广泛应用。人们提出了许多实现混沌同步的方法，例如，P-C同步法，主动被动分解法，耦合控制法和广义同步法等等。最近，文献[3]基于Lyapunov稳定性理论，实现了带有非线性项的分数阶混沌系统的稳定性。本文利用稳定性理论，在误差系统保留非线性项的情况下，实现了文中所提出的系统的同步，并且通过数值模拟验证了结论的正确性。

1预备知识

1.1分数阶导数定义

分数阶微分有着多种定义[1]，本文采用Caputo分数阶导数。

定义：令f∈Cm,m∈N. 函数f(t)的α阶Caputo导数定义为：

1.2稳定性定理

定理1[4]对于分数阶线性系统：

(1)

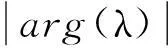
定理2[5]对于分数阶非线性系统：

(2)

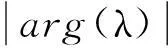
2新分数阶混沌系统

2.1新分数阶混沌系统的提出

文献[2]提出了三维整数阶广义Sprott C系统，其对应的分数阶系统为：

(3)

其中a≠0,b>0,且0<α≤1.

在上述系统(3)中增加一个变量v，构成一个四维新分数阶系统：

(4)

其中a≠0,b>0,d>0,且0<α≤1.

2.2新分数阶混沌系统的动力学分析

2.2.1对称性和不变性

2.2.2平衡点及其稳定性分析

(5)

根据(5)式可得特征方程为：

(6)

由于已知d>0，考虑下面方程的根的情况：

(7)

根据Routh-Hurwitz判别法[6]，如果满足条件：

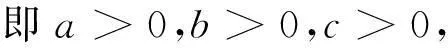
(8)

方程(7)则有三个具有负实部的特征根。根据定理2，此时平衡点E1显然是渐近稳定的。

进一步应用Routh-Hurwitz判别法，如果满足条件：

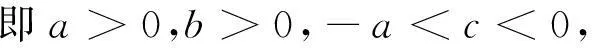
(9)

则方程(7)有一个负实根和一对具有正实部的共轭复根。假设λ1<0和λ2,3=β±γi(β>0)是方程(7)的三个根，那么有

(10)

即

(11)

比较(7)式与(11)式可得：

(12)

解得：

(13)

所以，

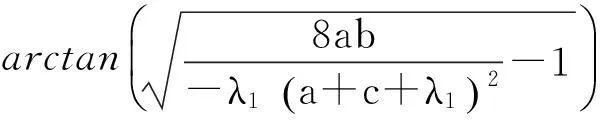
(14)

同理可知，平衡点E2有相同的结论。所以，根据以上分析，有以下定理。

2.3数值模拟

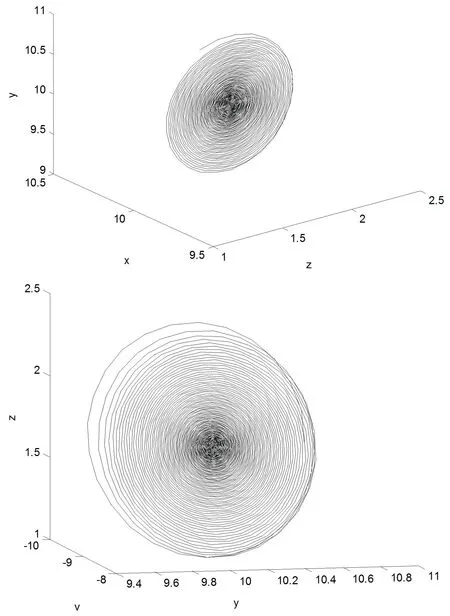
图1　在E1附近取初值

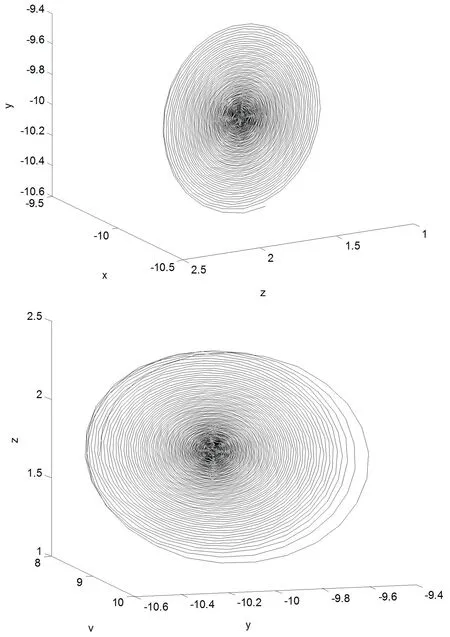
图2　在E2附近取初值

图3　系统(4)的混沌吸引子

3同步

3.1同步分析

设驱动系统为：

(15)

响应系统为：

(16)

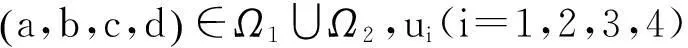
设同步误差为ei=yi-xi,i=1,2,3,4，若取控制器为：

(17)

则有误差系统：

(18)

构造如下的Lyapunov函数：

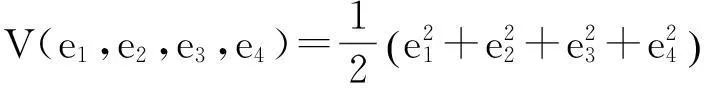
则根据文献[3]中的引理1，有V的分数阶导数为：

(19)

所以，根据分数阶Lyapunov稳定性理论，有以下定理成立。

3.2数值模拟

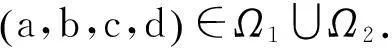
图4　系统(18)与(19)同步时间序列图

4结论

本文构造了一个新的四维分数阶混沌系统，此系统仅带有两个稳定平衡点。首先，分析了两个平衡点局部渐近稳定的充分条件，并通过数值模拟验证了平衡点的渐近稳定性，以及该系统的混沌吸引子可以和两个稳定平衡点共存。随后，基于分数阶Lyapunov稳定性理论，在误差系统保留非线性项的情况下，利用非线性控制器实现了此系统的同步，数值模拟进一步证实了结论的正确性。

[参考文献]

[1]Podlubny I. Fractional differential equations[M]. Academic press, 1998.

[2]Wei Z, Yang Q. Dynamical analysis of the generalized Sprott C system with only two stable equilibria[J]. Nonlinear Dynamics, 2012, 68(4), 543-554.

[3]Aguila-Camacho N, Duarte-Mermoud M A, Gallegos J A. Lyapunov functions for fractional order systems[J]. Commun. Nonlinear Sci, 2014, 19(9), 2951-2957.

[4]Matignon D. Stability results for fractional differential equations with applications to control processing[C]. Computational engineering in systems applications. Lille France, 1996, 2, 963-968.

[5]Diethelm K, Ford N J. Analysis of fractional differential equations[J]. J. Math. Anal. Appl. 2002, 265(2), 229-248.

[6]Barnett S. Polynomials and linear control systems[M]. Marcel Dekker, Inc., 1983.

[7]Diethelm K, Ford N J, Freed A D. A predictor-corrector approach for the numerical solution of fractional differential equations[J]. Nonlinear Dynamics, 2002, 29(1-4), 3-22.

Chaos and Synchronization of a 4D Fractional Order System with only Two Stable Equilibriums

WU Ranchao, ZHAO Yuhan

(SchoolofMathematicScience,AnhuiUniversity,Hefei230039,China)

Abstract：In this paper, a new fractional order four-dimensional autonomous chaotic system is proposed. It is found that it has only two stable equilibriums different from general fraction order chaotic systems, which often has unstable equilibrium points. First, some sufficient conditions for local stability of equilibriums are given. It is confirmed by numerical simulation in which chaotic attractors can coexist with two stable equilibriums. Then synchronization between such systems is analyzed. By Lyapunov stability theory, synchronization is realized while the error system is still kept to be nonlinear. Numerical simulations are performed to verify the theoretical results.

Key words：fractional order system; local stability; chaos; synchronization

[中图分类号]G61

[文献标识码]A

[文章编号]1674-2273(2015)06-0039-04

作者简介][第一 吴然超(1971-)，男，安徽六安人，安徽大学数学科学学院教授，博士生导师，研究方向：微分方程与动力系统。

[基金项目]安徽省自然科学基金(11040606M12)

[收稿日期]2015-04-06