八叉树空间结构投影的射线物体求交方法

魏潇然,耿国华,张雨禾

(西北大学 信息科学与技术学院，陕西 西安 710127)



·信息科学·

八叉树空间结构投影的射线物体求交方法

魏潇然,耿国华,张雨禾

(西北大学 信息科学与技术学院，陕西 西安 710127)

为了提高光线投射算法中射线与物体求交速度,提出一种利用八叉树空间结构在视平面上投影的射线快速求交方法。算法构造平行于视平面的八叉树空间结构,将每个八叉树叶子包围盒沿视点方向投影在视平面上,将视平面划分成若干投影区域。在射线与包围盒求交时,根据射线落在视平面上的位置,确定其所属投影区域,求出与该射线相交的包围盒。实验表明该算法对传统的光线投射算法效率有较大提升。

射线求交；投影；八叉树；光线投射

光线投射是图形学中的常用绘制技术之一,在体绘制中有着广泛的应用。利用光线投射进行绘制的计算开销较大,妨碍了其应用效率。通过实验验证和理论分析可知,这些绘制计算中开销的绝大部分用于光线与构造场景的图元的求交计算。为此,人们研究了大量的技术来加快求交计算,其中,通过建立一定的空间组织结构来加速线面求交是这方面的主要研究内容之一。大量的空间组织结构被应用在线面求交中,如基于物体划分的层次包围盒[1]、基于空间划分的均匀网格[2-3]、八叉树[4]、k-d 树[5-6],以及结合这两种划分方式的混合结构[7]等。这些结构各有特点,需要根据所处理场景的特点及绘制任务进行相应的选用,没有哪一种能最优地处理各种场景。

一般加速空间结构中通常采用包围盒结构划分三维场景,首先用射线与包围盒求交,之后再用射线与包围盒内图元求交。本文选取八叉树空间结构,针对射线求交过程中大量射线与包围盒求交计算进行了优化,将包围盒在视平面上的投影,将射线与包围盒求交计算转换为射线在屏幕上的投影区域的求交计算,减少了射线求交的计算量。

1 八叉树投影的射线求交算法原理

首先对本文出现的一些术语进行定义:视点定义为o,视点坐标为(0,0,0);屏幕所在平面定义为视平面,视平面原点为视点在视平面的投影点,沿屏幕长宽边分别定义视平面的u方向和v方向,u和v方向正交;八叉树结构最外层对整个三维场景的包围盒称为八叉树外包围盒;八叉树某一叶子节点上表面所属平面与八叉树外包围盒相交,相交区域称为八叉树的一个截面,如图1所示。

视点发出的射线定义为r(t)=o+td,其中o代表射线出发点,t代表光线沿z轴行驶距离,d为光线的方向向量,l1为视点到视平面的距离。

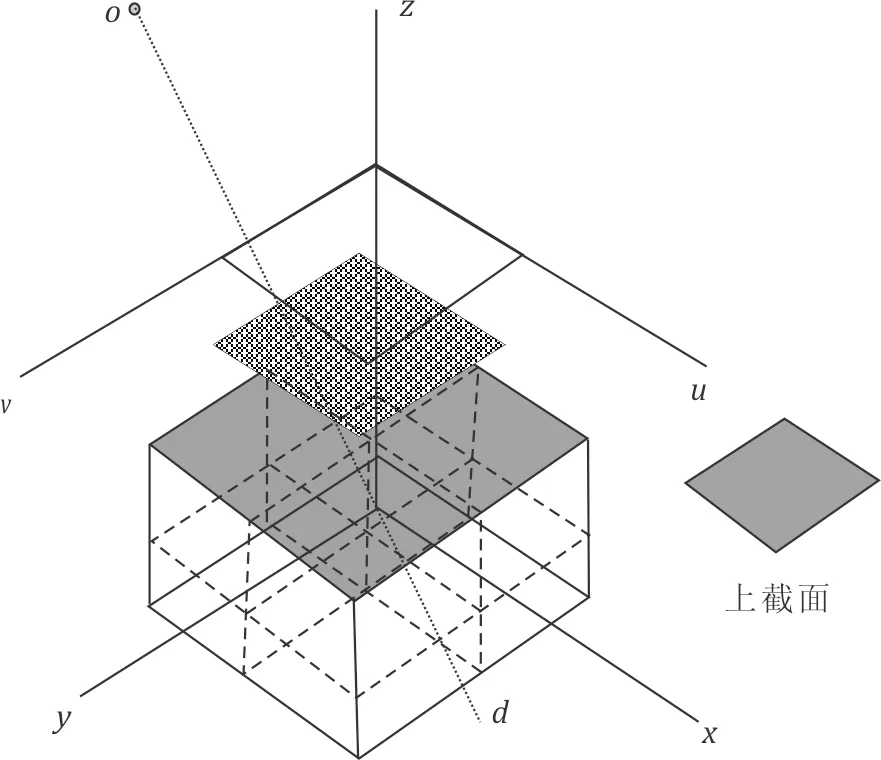
图1 术语说明Fig.1 Terminology illustraion

光线投射原理如图2所示,从视点发出射线到视平面的每个像素,穿过视平面到达场景数据中,对相交图元进行采样,并进一步计算该图元的颜色信息,从而完成绘制过程。

图2 光线投射原理图Fig.2 Principle of ray casting

本文算法对这射线图元求交过程进行了优化,在原有的八叉树空间加速结构基础上,将八叉树每个叶子节点包围盒投影到屏幕上,形成一组投影区域;射线落在屏幕上一点,得到该落点所属的投影区域对应的叶子节点,射线穿过该叶子节点包围盒;若落点属于多个投影区域,则落点对应多个叶子节点,射线按照这些叶子节点与视点的距离,依次穿越这些叶子节点。

下面对原理进行相关证明:

证明1 若长方体包围盒平行于视平面,其上表面在视平面上投影为长方形。

本文构建一个平行于视平面的八叉树外包围盒,以垂直于视平面方向为八叉树外包围盒高方向,视平面上u，v轴方向为八叉树外包围盒长、宽方向。

如图3所示,A2B2C2D2为八叉树叶子节点包围盒的一个上表面,A1B1C1D1区域为A2B2C2D2沿视点方向向视平面的投影。

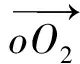
|A1B1|=

|A2B2|=

可知|A1B1|/|A2B2|=l1/l2,同理可证|B1C1|/|B2C2|=l1/l2,|C1D1|/|C2D2|=l1/l2,|D1A1|/|D2A2|=l1/l2。

A2B2C2D2为长方形,故A1B1C1D1也是一个长方形,并且与A2B2C2D2长宽成比例,比例为l1∶l2。

故叶子节点包围盒上表面在视平面上投影为长方形,并且投影长方形的长宽跟上表面所属平面到视点的距离成比例。

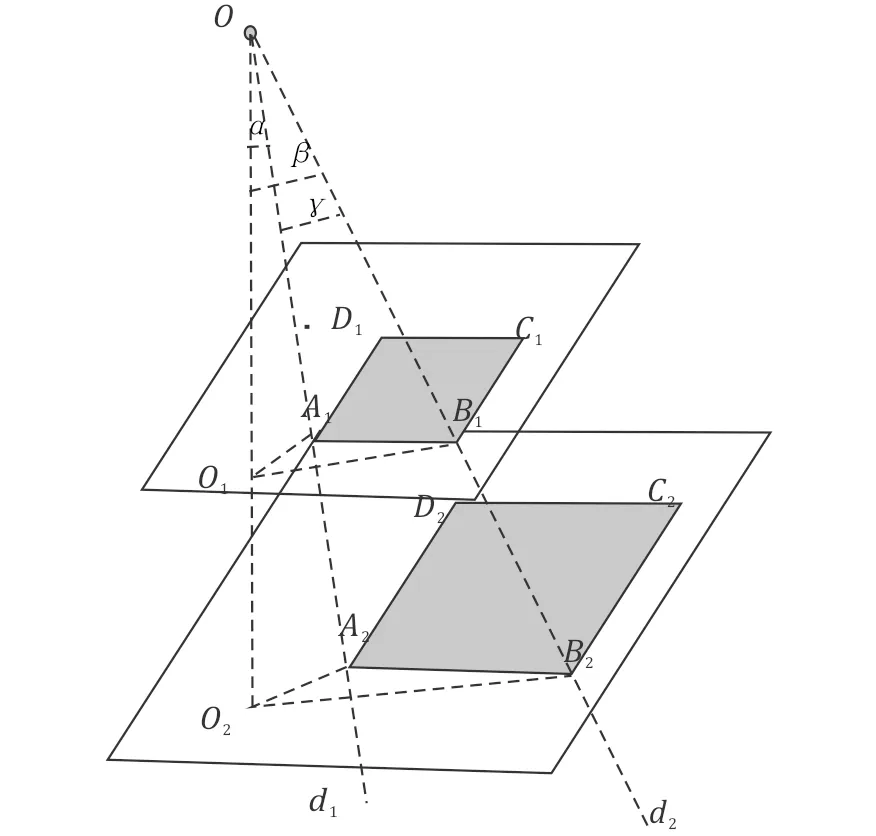
图3 叶子节点包围盒上表面在屏幕投影Fig.3 Top surface of the leaf bounding volume projection on the screen

证明2 八叉树叶子包围盒投影区域连续性

图4a和图4b所示为八叉树一叶子包围盒上下表面到屏幕投影。计算当八叉树空间中任意一点V1(x0,y0,z0)沿z轴移动δc至V2(x0,y0,z0+δc)时,V1和V2点在投影视平面上的位置U1和U2。

根据射线公式V1(x0,y0,z0)=o+z0d1,V2(x0,y0,z0+δc)=o+(z0+δc)d2,得到d1=(x0/z0,y0/z0,1),d2=(x0/(z0+δc),y0/(z0+δc,1),V1,V2在视平面的投影U1,U2可以根据射线公式求得

U1(u0,v0,l1)=o+l1d1=

U2(u1,v1,l1)=o+l1d2=

通过该公式可知,下层一点与上层同位置点(x,y坐标相同)在投影面位移为

δU=U1-U2=

l1*(δc*x0,δc*y0,0)/z0*(z0+δc)。

(1)

八叉树空间结构中一点沿z轴变化时,位移后投影点(u,v)可以计算如下

(u,v)=l1*(x0,y0)/z0+

(2)

根据该公式可得g(u)=(x0/y0)v,g(u)为线性方程,故八叉树任一点V(x0,y0,z0)沿z轴移动,其投影屏幕上的投影点U(u,v)以(x0/y0)的比例向原点以线性连续方式移动。

八叉树叶子节点包围盒可以看做由上表面所有点沿z轴方向向下移动一定距离生成。由于八叉树叶子节点上表面在视平面的投影是一个长宽分别平行于u轴和v轴的长方形,若视平面原点在上表面投影内部,则上表面上所有点沿z轴向下移动的投影均向原点移动,整个包围盒的其他点投影均在上表面内部,如图4a所示,此时投影区域连续。若原点不在上表面内部,上表面中x/y最大最小点的投影必在其两个顶点处。八叉树叶子节点上平面任意一点在该包围盒范围内向下移动,其投影均在其上下表面顶点围成的多边形内,如图4b所示。连接上下表面对应顶点后形成的区域为包围盒在视平面上的投影,该区域连续。

若视点发出的射线落在投影区域内，则该射线与该八叉树叶子节点存在交点。

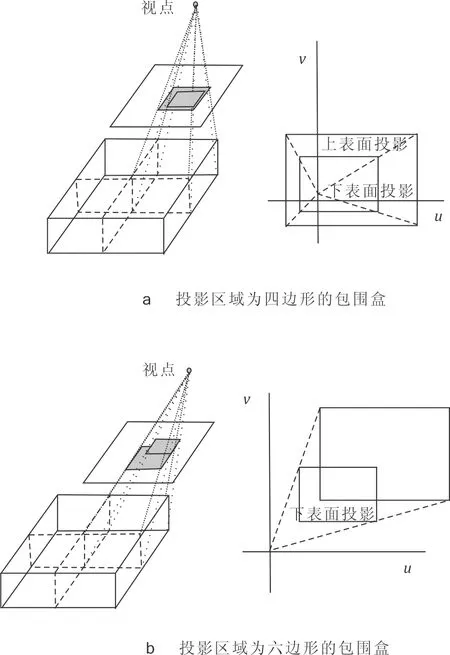
图4 八叉树叶子包围盒上下表面到屏幕投影Fig.4 Surface of the leaf bounding volume projection on the screen

下面对投影区域的快速计算法方法进行说明:

设i为叶子包围盒深度,视点到视平面距离为l1,视点到叶子节点上平面距离为l2。由该叶子节点深度计算得到该叶子节点包围盒长宽高分别为a，b，c,利用射线公式计算出八叉树最上截面上任意一叶子节点上表面左下角点在屏幕上投影坐标U0(u0,v0),上表面在视平面的投影长宽为a*(l1/l2),b*(l1/l2),可知上表面4顶点坐标;下表面在视平面投影长宽为a*(l1/(l2+c/2i)),b*(l1/(l2+c/2i))。上下表面在视平面上的投影长宽比为(l2+c/2i)/l2,故根据上层投影长方形的长宽可以计算得到下层投影长方形的长宽。

利用公式1,由上表面左下角点投影坐标计算在下表面的对应点的坐标,之后根据下表面投影长方形的长宽快速计算投影长方形4顶点。之后根据上下表面的八个投影顶点即可迅速计算出其所围成的投影区域。

2 八叉树投影的射线求交算法实现

本算法实现分为两部分,第一部分为八叉树空间结构初始化及八叉树叶子包围盒投影图预计算,可以细分为构造八叉树数据结构、八叉树叶子包围盒的视平面投影区域计算和生成投影区域图;第二部分为射线图元求交,根据投影图求出与射线相交的包围盒,再求出包围盒内与射线相交的图元。

2.1 构造八叉树数据结构

本文算法采用紧八叉树空间结构,划分的步骤为:

1) 根据第1节所述,构造长宽平行于视平面的u,v轴,高垂直于视平面的场景外接包围盒,计算出该包围盒的最小Vmin和最大Vmax,通过计算Vmin和Vmax得到中间矢量Vinter,Vinter=(Vmax+Vmin)/2;

2)通过Vmin，Vmax，Vinter对场景包围盒进行八等分,获得8个子包围盒;

3)循环判断是否有与子包围盒相交的面片,如果没有则删除该包围盒,如果有则获得指向相交面片集的指针;

4)判断是否达到停止剖分条件,如果没有则继续向下剖分8个子包围盒;

5)满足停止剖分条件后,将该节点记录为八叉树叶子节点,并记录该节点层次数。

终止条件采用两条件共同约束,1)当前包围盒内叶子节点数少于阈值N时停止划分，2)当八叉树层次超过M层时停止划分。

在构造完成后对八叉树叶子节点进行排序编号,以便在后续投影图中确定射线进入八叉树包围盒的顺序。

编号方法如下:

1)首先从八叉树的最上层截面开始排序,因为该截面在任何情况下都存在一点在包围盒中距离视点最近,求出视点在该层上的投影点,寻找距离该投影点最近的叶子包围盒节点;

2)依照该截面其他包围盒距该包围盒的距离排序,同样距离情况下,深度较深的叶子包围盒排序在先;

3)寻找下一待排序截面。首先求出所有未排序叶子节点中上层z坐标最大,该叶子包围盒的上表面为下一待排序截面;然后获取该截面所包含的所有叶子节点包围盒,对新求出的截面所有叶子节点包围盒以步骤2)方法进行排序,序号在之前排序顺序后累加;

4)重复步骤3),直到所有叶子节点均排序完成。

图5所示为八叉树一截面的顺序编码,叶子包围盒0为与视点最接近的包围盒。利用该方法编号后,一条光线穿过一组包围盒时,先进入的包围盒编号必然会小于后进入的包围盒。

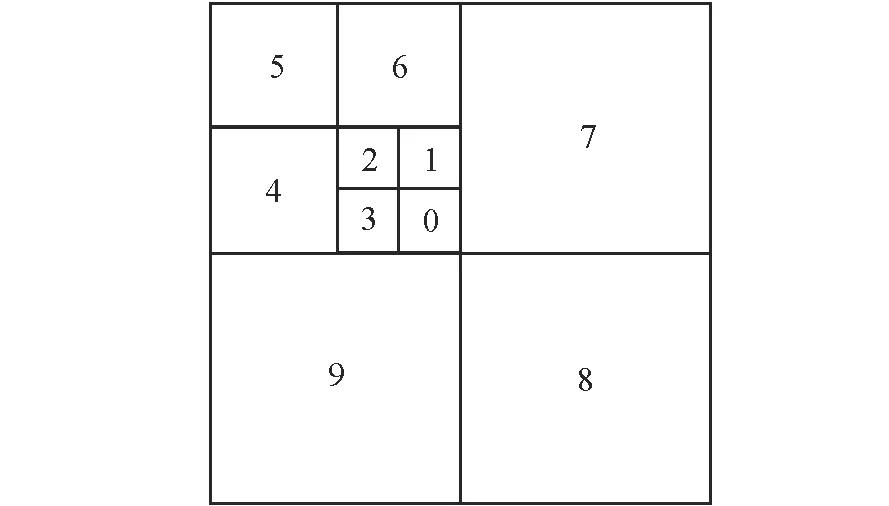
图5 包围盒排序编号Fig.5 Sorting of the bounding volume

2.2 计算八叉树叶子包围盒到屏幕投影

结合第1节中投影八叉树的性质和投影区域的快速计算方法,采用以下步骤,可以迅速求出八叉树所有叶子包围盒到屏幕的投影:

1)计算任意叶子节点包围盒上表面左下角点在屏幕的投影,之后根据该包围盒深度,求出该包围盒长宽高,根据第一节中节推论计算出上表面在视平面上的投影;

2)根据叶子包围盒的高算出和以叶子包围盒上表面的投影,结合第1节中的上下表面长宽比例公式及位移公式,计算得到下表面的投影区域;

3)若视平面原点在上表面投影区域内,则叶子包围盒投影区域为上边面投影区域,如图4a右图;否则,连接上、下表面对应的四顶点,并求外接多边形,可以得到叶子节点包围盒在屏幕的投影区域,如图4b右图;

4)求该叶子的相邻叶子节点的投影平面,利用1)中求得出的端点坐标,寻找这些端点的其他叶子包围盒,之后按照步骤1)～3)求出其投影区域。

最终，自上而下生成所有叶子包围盒的投影。

2.3 生成投影区域图

由于每个叶子包围盒都对应了一块投影区域,整个八叉树空间结构会存在非常多的叶子包围盒投影区域,故需要对这些投影区域作进一步整合,以加快后续的求交运算。

可以将若干投影区域组成一张投影图。现举例说明两类投影图组成方式,其中投影图中坐标与视平面坐标保持一致:

方式1 将所有叶子包围盒的投影区域组成一副图像,以叶子包围盒的编号对每个投影区域编号,若多个叶子包围盒的投影区域存在相交,则将这些包围盒的标号全部赋予相交区域。该方法使用起来比较直接,只需保存一幅图像,适合用在叶子包围盒数量较少的场景。

方式2 将同截面的叶子包围盒的投影区域组成一副图像,以叶子包围盒的编号对每个投影区域编号,若多个叶子包围盒的投影区域存在相交,则将这些包围盒的标号全部赋予相交区域。该方式存储一组图像,射线求交时从上到下的顺序遍历所有图像,即可求出所有相交图元。该方式适合用在叶子包围盒数量较多的场景。

2.4 光线投射算法中的射线图元求交

光线投射算法需要求出射线穿越的图元。利用2.3节生成投影区域图判定射线与包围盒是否相交,之后再求出与射线相交的图元信息,本文采用方式二生成的多幅投影区域图进行求交判断,具体步骤如下:

1)首先获取光线与视平面的交点,之后依次搜索投影图,获取包含该交点的所有投影区域,并按区域中包含的叶子包围盒编号由小到大顺序记录。

2)根据编号获取每个区域对应包围盒,计算包围盒中与射线相交的图元。

获取这些交点信息后,对交点图元的色彩和透明度进行采样,并用色彩合成算子进行色彩的累计,获取该点最终色彩。

按上述方法依次获取所有所有点的绘制,完成数据的绘制。

3 实验结果分析

本文算法所采用的实验环境如下:CPU采用Intel(R)Core(TM)i7X980,显卡采用NVIDIAQuadro4000,内存为16GB。

实验取不同射线数分别进行了测试,并对同一模型八叉树结构用多种深度分割进行了反复测试,最优深度为绘制速度最快时八叉树的深度，表1中仅列举最优深度时的测试信息,实验比较了传统八叉树包围盒算法下绘制速度与使用本文算法的绘制速度。本文所用数据如图6所示。实验结果如表1所示。

图6 实验数据Fig.6 Experiment data

表1 传统光线投射算法和本文算法绘制时间对比Tab.1 The contrast of rendering time of traditional ray casting and the algorithm in this paper

实验结果显示：①利用本文算法,最优层次数增加。这是由于射线包围盒求交的运算量减少,使得可以划分更深层次的八叉树,相应的包围盒内的平均图元数也减少,使得在求包围盒内与射线相交的图元时计算量减少;②在光线跟踪数量增加的情况下,算法效率有了提升,这主要是由于投影区域之间存在关联性,编码时可有效利用这些关联性,减少了计算量;③本文算法所使用的平均绘制时间为传统算法的47.6%,实验证明算法可以有效的提升射线图元求交及光线投射算法的速度。

4 结 语

本文提出了一种射线与包围盒求交的快速算法,与已有求交方法相比,算法对八叉树空间结构进行预处理，预先计算八叉树叶子节点包围盒在屏幕上的投影,再利用投影图进行求交运算,减少了包围盒与射线求交的计算,将算法应用到光线投影中,取得了良好的效果。如何将该算法用在光线跟踪等其他渲染算法中可以作为下一步研究重点。该算法可以推广到k-d树,均匀网格等其他加速空间结构中,这同样也是未来将拓展的工作。

[1] WALD I, BOULOS S, SHIRLEY P. Ray tracing dynamic scenes using deformable bounding volume hierarchies[J]. ACM Transactions on Graphics, 2007,26(1):1-18.

[2] WALD I, IZE T, KENSLER A, et al. Ray tracing animated scenes using coherent grid traversal[J]. ACM Transactions on graphics, 2006, 25(3): 485-493.

[3] IZE T, WALD I, ROBERTSON C, et al. An evaluation of parallel gird construction for ray tracing dynamic scenes[C]//Proceedings of IEEE Symposium on Interactive Ray Tracing, Salt Lake City, 2006: 47-55.

[4] PENG Q S, ZHU Y N, LIANG Y D. A fast ray tracing algorithm using space indexing techniques[C]//Proceedings of Eurographics′87. North Holland: Elsevier Science Publishers, 1987: 11-23.

[5] RESHETOV A, SOUPIKOV A, HURLEY J. Multi-level ray tracing algorithm[J]. ACM Transactions on Graphics, 2005, 24(3):1176-1185.

[6] WALD I, HAVRAN V. On building fast k-d trees for ray tracing, andDOIng that in O(NlogN)[C]//Proceedings of IEEE Symposium on Interactive Ray Tracing. Salt Lake City: IEEE Press，2006: 61-69.

[7] KLIMASZEWSKI K, SEDERBERG T W. Faster ray tracing using adaptive grids [J]. IEEE Computer Graphics and Applications, 1997, 17(1): 42-51.

[8] STEIN C, LIMPER M, KUIJPER A. Spatial data structures for accelerated 3D visibility computation to enable large model visualization on the web[C]//Proceedings of the Nineteenth International ACM Conference on 3D Web Technologies. New York: ACM Press, 2014: 53-61.

[9] 康健超,康宝生,冯筠,等.基于八叉树编码的CUDA光线投射算法[J].西北大学学报(自然科学版)，2012,42(1): 36-41.

(编 辑曹大刚)

A ray intersection method based on octree spatial structure′s projection

WEI Xiao-ran, GENG Guo-hua, ZHANG Yu-he

(Information and Science College, Northwest University， Xi′an 710127， China)

In order to improve ray intersection with the object speed in ray casting. Proposed a fast ray intersection method using octree spatial structure′s projection on the viewing plane. Constructed an octree spatial structure parallel to the viewing plane, then project octree leaves′ bounding volume along the viewing direction to the viewing plane, viewing plane is divided into lots of blocks of the projection area. In the ray intersection with the bounding volume, the ray falls on the viewing plane, determining its respective projection area, and then finding the ray intersects the bounding volume. Experimental results show that the algorithm can speed up the efficiency of the ray intersection compared with the traditional method.

ray intersection; projection; octree; ray casting

2014-11-04

国家自然科学基金资助项目(61373117)

魏潇然，男，博士生，陕西咸阳人，从事计算机图形学、虚拟现实、3D打印等研究。

TP391

：ADOI：10.16152/j.cnki.xdxbzr.2015-03-006