非牛顿流体在变截面管中流动的数值模拟
李玉伟,方小里,李召生,曹丽琴
(1.哈尔滨锅炉厂有限责任公司,哈尔滨150046;2.燕山大学环境与化学工程学院,河北 秦皇岛 066004)
非牛顿流体在变截面管中流动的数值模拟
李玉伟1,方小里1,李召生1,曹丽琴2
(1.哈尔滨锅炉厂有限责任公司,哈尔滨150046;2.燕山大学环境与化学工程学院,河北 秦皇岛 066004)
由于非牛顿流体的粘度随剪切速率而变化,使得其在流动时表现出十分复杂的规律,这给实际应用和研究带来困难。文中应用数值模拟方法对非牛顿流体在二维变截面管中的非稳态流动进行了研究。研究发现,对于非牛顿流体,考虑粘度随剪切速率变化时的工况与考虑粘度为固定值时的工况相比,流动更加复杂,流场也更加紊乱,管道中心区的速度明显增加;同时,在截面突然变化的区域,流体的压力和速度波动也更加剧烈,下游区域往往会形成大量的旋涡,这对流体流动的均匀性产生巨大的影响。在同一周期的不同时刻,流场中的压力和壁面剪切力也表现不同的变化物性。
非牛顿流体;非定常流动;变截面管;旋涡;数值模拟
0 引 言
在工业生产和自然界中,存在着许多剪切应力与剪切速率不呈线性关系的流体,称之为非牛顿流体。人身上的血液、淋巴液,以及油漆、油脂、牙膏、泥浆等都是非牛顿流体。近几十年来,促使非牛顿流体研究迅速开展的主要动力之一是聚合物工业的发展。聚乙烯,涤纶,橡胶溶液,各种工程塑料,化纤的熔体、溶液等都是非牛顿流体[1]。
非牛顿流体力学是上世纪50年代发展起来的一门新兴边缘学科。它主要研究非牛顿流体的流变性质及其运动规律,是现代流体力学的重要分支,同时它也是现代流变学的重要组成部分。在最近的30年里,非牛顿流体力学己经成为了流变学的一个重要的而且十分活跃的分支。在最近几届流变学国际会议中,非牛顿流体力学都成为了会议讨论的主要问题[2]。
由于非牛顿流体的粘度不是定值,使得对其流动的研究十分复杂。应用传统的实验方法对其进行研究时,实验不仅耗时长,而且耗资昂贵;而由于非牛顿流体的控制方程严重的非线性,直接应用理论分析方法求解往往无能为力。随着CFD技术的飞速发展,数值计算方法得到了日益广泛的应用。应用数值计算方法,往往能得到传统研究方法无法获得的结果。
1 计算模型
文中采用简化的二维计算模型如图1所示。在管道的前半部分,上壁面形成了一个尖状缩喉,位于x/L=0的处,长度为2 L,其中L为管道截面高度:6 mm。这个缩喉使得管道截面积缩小了一半,在缩喉的上游区域管道长为5 L,在缩喉的下游区域管道长为15 L。

图1 二维流场模型简图
假定流体为均匀不可压的非牛顿流体,控制方程为2D Navier-Stokes 方程及质量守恒方程。其中流体的密度为1 060 kg/m3,而考虑粘度时,本文采用以图2为基础的通过拟合所得的粘度计算公式。从粘度变化曲线可以看出:在剪切速率很小时,粘度具有很大的数值;但随着剪切速率的增加,粘度迅速减小,并最后趋于定值。
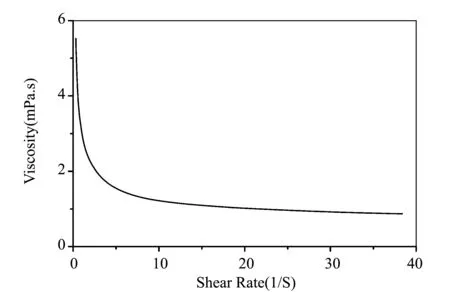
图2 粘度随剪切率的变化
在CFD数值计算中,上下壁面采用无滑移边界条件,入口截面设为速度入口,出口截面采用对流边界条件,设置压力为1.33×104Pa[4-5]。为加快收敛速度、优化计算,本模型采用结构化的四边形网格,并在在靠近壁面处对网格进行了加密,以捕捉近壁面处的流动细节。
入口截面上的速度分布为正弦曲线,同时,对于非定常流动,速度将随时间发生变化,公式如下[5]:
(1)

2 结果与讨论
为了更加清楚的了解此非牛顿流体的流动特性,文中将把计算结果与另一种工况,即假定流体的粘度为一固定值时的结果相比较,其中后者的粘度恒为0.003 71 mPa·S。
图3中显示了同一时刻两种工况下的压力分布特性,其中(a)为变粘度非牛顿流体的压力分布,最大压差为256 Pa;(b)为恒粘度非牛顿流体的压力分布,最大压差为233 Pa。从入口和出口截面上的压力值可以看出,在通过同一管道时,变粘度流体的压降比恒粘度流体的压降大得多,约为后者的两倍。但变粘度流体的最低压力点不仅位于缩喉的顶端(该区域由于管道截面急剧减小,流体速度迅速增加,导致静压降低),而且在其下游约x=2 L处存在一个低压区,这和恒粘度流体的低压区仅仅位于缩喉顶端是不一致的。

图3 压力分布
不同工况下的速度的分布特性在图4中进行了比较。从图(b)中可以看到,对于恒粘度非牛顿流体,其速度峰值区域正好位于尖状缩喉之后并且迅速衰减,长度只有约2.5 L。在此之后,管道中速度逐渐趋向均匀分布。同时,在上壁面紧靠缩喉处存在一个大的负速度场,即流体向左流动,这是因为在该区域形成了一个旋涡。比较图(a)中变粘度非牛顿流体的速度分布,可以看到在管道的中心部分,其流速较大,并且其速度峰值分布的区域更长,约延伸至5 L处。同时,在该区域范围内上下壁面各存在一个旋涡区。对于变粘度非牛顿流体所表现出的这种特性,我们可以从它的粘度值随速度梯度的增大而减小中得到解释(在速度变化更加剧烈的区域,其粘度反而很小,速度的衰减因而更加缓慢)。

图4 轴向速度分布
关于变粘度非牛顿流体的流场中出现的旋涡,我们可以从图5中的速度矢量图中得到进一步了解。可以看到,流场中共有4个大的旋涡:上壁面处有3个,分别位于x/L=1、2、5处;下壁面处存在1个,位于x/L=4处,这和对图4的讨论结果是一致的。

图5 变粘度非牛顿流体速度矢量

图6 上、下壁面上的瞬时压力

图7 上、下壁面上的瞬时剪切应力

3 结束语
文中研究了在二维流场中有关非牛顿流体的非定常流动问题。结果表明, 变粘度非牛顿流体的流动特性与传统的流体有很大的区别。对于非牛顿流体,正是由于其粘度变化的特殊性,导致其在流动方面表示出不同的变化规律。主要表现在:
(1)变粘度非牛顿流体的速度衰减与恒粘度非牛顿流体相比更加缓慢。这是因为,变粘度非牛顿流体的粘度随速度梯度的增大而减小,对流体流动的阻碍减小。
(2)管道截面的突然变化,使流体在下游区域出现剧烈波动,压力和速度大小变化很大。同时,在变粘度非牛顿流体的流场中,更容易出现旋涡。
(3)在一个周期中的不同时刻,流体表现出不同的特性。速度较低时,沿轴向压力可能反而增大。这是由于动压衰减而转化为静压的结果。
[1] 马 倩. 非牛顿流体在环管中流动与换热特性的数值研究[D]. 南京理工大学,2007.
[2] 张明侃. 非牛顿流体在旋转曲线管道内的对流换热研究[D]. 浙江大学,2008.
[3] Barbara M. Johnston, Peter R. Johnston, Stuart Corney, David Kilpatrick. Non-Newtonian blood flow in human right coronary arteries: Transient simulations. JOURNAL OF BIOMECHANICS, 2006, 39: 1116-1128.
[4] 张治国,樊瑜波,邓小燕,等.Guidoin Robert. 一种带有旋动流引导器的新型小口径人造血管流场的数值模拟. 中国科学 C辑:生命科学. 2008,38(9): 807-815.
[5] Manosh C. Paul, Md. Mamun Molla, Giles Roditi. Large-Eddy simulation of pulsatile blood flow. Medical Engineering & Physics, 2009, 31: 153-159.
Numerical Simulation on Non-newtonian Fluid Flow in a Variable Cross-section Tube
LI Yu-wei1, FANG Xiao-li1, LI Zhao-sheng1, CAO Li-qin2
(1. Harbin Boiler Works Co., Ltd. Harbin 150046, China;2. Yanshan University, School of Environmental and Chemical Engineering, Qinhuangdao 066004, Hebei Province, China)
The viscosity of non-Newtonian fluid depends on the shear rate, which makes the flow very complex, and increases the difficulty to practical application and research work. This paper numerically studies an unsteady non-Newtonian flow in a two-dimension tube with variable across-section. It shows that for the non-Newton fluid, the pattern of the flow is more complex and the field is more disordered with a higher velocity at the centre of the tube in the case with the viscosity changing with the shear rate than in the case with a constant viscosity. In the region of the throat, the pressure and the velocity of the fluid fluctuate significantly and many vortices form at the downstream region, which have a significant contribution to the homogeneity of the flow. At different phases in a period, the pressure and wall shear stress performance differently too.
Non-Newtonian fluid; Unsteady flow; Variable cross-section tube; Vortices; Numerical simulation
2015-03-09
2015-03-21
李玉伟,男,工程师,从事压力容器常规设计、SAD压力容器的设计工作。
10.3969/j.issn.1009-3230.2015.04.001
TH138.1
B
1009-3230(2015)04-0001-04

