一种无人机载制导炸弹姿态测量方法
张晓龙,朱平安
(陆军军官学院,合肥 230031)
近年来,研究无人机武器化手段之一的机载制导炸弹成热门趋势,而对于制导炸弹飞行姿态确定是导引控制其飞向指定目标的先决条件。为此,本文在基于GPS制导炸弹上搭载地磁传感器等微型器件来测量弹体在飞行过程中的姿态,通过地磁传感器、角速率传感器确定姿态角后,以气压传感器辅助测高的GPS信号和注入弹体的目标样本参量来确定弹目之间的调整角度,以此来形成导引弹体飞向目标的舵控指令。
1 姿态测量原理分析
1.1 基于GPS的制导原理
由目标样本的地理坐标与弹载GPS提供的弹体质心位置坐标,可以确定弹体与目标之间的空间位置关系,GPS制导的过程就是将弹体导引到弹目连线上,并将弹体头部调整到向目标飞行方向。如图1所示,以弹体质心为原点ob,xb,轴为弹体纵轴线,onhb为xb轴在水平面上的投影,onhm为弹目连线obhm在水平面上的投影。某一时刻弹体姿态由地理坐标系中偏航角ψ和俯仰角θ确定,弹体与目标的相对空间位置关系可以看作是将xb轴经过水平方面偏转α,再经过垂直方向俯仰β,即xb轴与弹目连线onhm重合,这样弹体姿态就调整到目标方向,形成弹体的制导。其中,α为 onhb与onhm的夹角,β为obhm与obh'm的夹角,这两个夹角就是修正弹体飞行轨迹的控制量。
在确定弹体姿态角后,利用空间几何关系可以计算得到α 和 β。
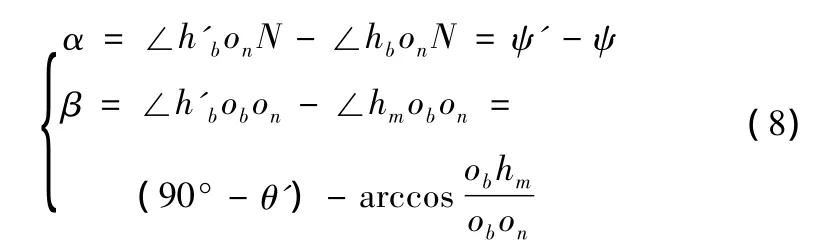
式中:ψ'和θ'分别为弹体经过偏转后的偏航角和俯仰角;obhm可根据弹载GPS和目标坐标确定;obon垂直于地面,可通过气压传感器测得(或是弹载GPS提供)。
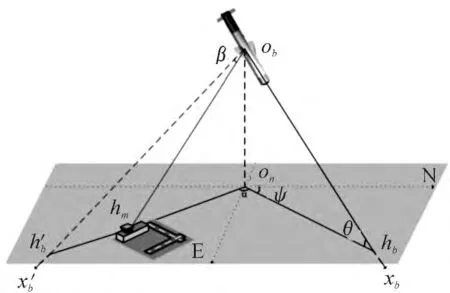
图1 GPS制导原理示意图
1.2 基于地磁传感器的姿态角测量
弹体姿态角即弹偏航角、俯仰角和滚转角,是指弹体在地球空间中的三维参数,通常用弹体坐标系的各个轴与地理坐标系的各个轴之间的夹角表示,利用地磁传感器测得的地磁信号,解算得到弹体的姿态角,也就确定了弹体的自身姿态。要确定弹体的姿态,首先要建立相关的空间坐标系,然后利用空间坐标系来定义姿态角,最后通过推导各个坐标系之间的转换关系即姿态矩阵来解算弹体姿态角[1,2]。
1.2.1 建立坐标系[3]
1)地理坐标系O-xnynzn
地理坐标系原点取在弹体质心,xn轴(N轴)在水平面内指向正北方向,yn轴(E轴)垂直于xn轴指向东,zn(D轴)垂直于xn、yn轴所组成的平面并符合右手定则,方向沿地垂线指向地。地理坐标系的各轴可以有不同的选取方法,上述这个坐标系也可以叫做北东地坐标系,还有以“东、北、天”或“北、西、天”为三轴顺序构成右手直角的地理坐标系。
2)弹体坐标系O-xbybzb
弹体坐标系以在弹体的质心为原点,xb轴沿弹体几何纵轴指向弹头方向,yb指向弹体的右侧,zb垂直于zb轴、yb轴并构成右手坐标系。弹体坐标系与弹体固联,是动坐标系。弹体坐标系相对于地理坐标系的方位即为弹体的姿态。
1.2.2 定义姿态角
弹体的姿态角在坐标系中表示如图2和图3所示。
偏航角ψ:弹体坐标系的xb轴在水平面上的投影与地理坐标系的xn轴之间的夹角,沿着xn轴(正北)向右偏为正,角度范围在(0°,360°);
俯仰角θ:弹体坐标系的xb轴与水平面(即xb轴在水平面上的投影)之间的夹角,Xb轴偏离水平面为正,角度范围在(-90°,90°);
滚转角γ:绕弹体坐标系的xb轴自转形成的夹角,沿着xb轴方向右偏转为正,角度范围在(-180°,180°)。为了能直观地表示,建立弹体横截面坐标系O-y1z1,从弹尾到弹头方向看,弹体横截面坐标系的y1轴到弹体坐标系的yb轴转过的角度即为滚转角。

图2 弹体偏航角与俯仰角的确定
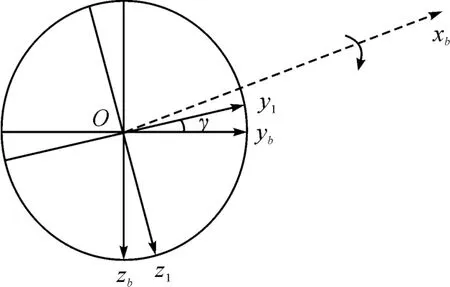
图3 弹体滚转角的确定
1.2.3 推导姿态矩阵
坐标系之间的转换一般包括平移和转动,由于坐标系都是以弹体质心为原点而建立,平移时没有改变坐标系的方向,因此在确立弹体的姿态时不需考虑坐标系的平移,只需做坐标系的转动变换。从地理坐标系转换到弹体坐标系需要方向余弦矩阵,它们之间的关系为
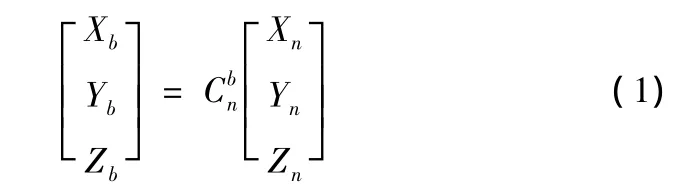
地理坐标系O-XnYnZn转换到弹体坐标系O-XbYbZb可通过以下顺序转换:首先,地理坐标系O-XnYnZn绕Zn轴旋转ψ得到坐标系O-X'nY'nZ'n,然后绕Y'n轴旋转θ得到坐标系 O -X″nY″nZ″n,最后绕 X″n轴旋转 γ 即可得到弹体坐标系。各次基本转换对应的方向余弦矩阵分别为
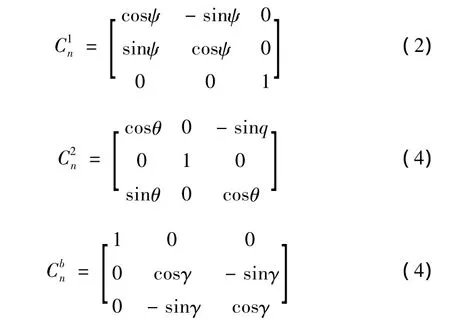

1.2.4 解算姿态角
本文运用三轴地磁传感器进行弹体姿态测量,正是由于地球磁场在地球表面约为0.5~0.6高斯的平行分量始终指向磁北方向,传感器可以输出沿敏感轴上的地磁场强度。将三个敏感轴沿弹体坐标系的三个轴放置,这样对于弹体质心在空间任意位置的磁场矢量,在弹体坐标系上的分量即为传感器敏感轴上的量测值,设为、和。同时,将磁场矢量分解在地理坐标系中,各个坐标轴上磁场分别设为、和。根据地理坐标系与弹体坐标系的关系,结合式(1)与式(5)可以得到弹体姿态角的关系式(6)。
经过计算整理则得出一个关于偏航角、俯仰角和滚转角的方程组如式(7)。从式(7)可以看出,姿态角ψ、θ、γ是关于三角函数的未知数,彼此之间相互关联,所以上式是三个非独立的方程式,该方程组不能直接求解,需要提供其他补充参考,才能求解出弹体姿态角。为此,设计时加入一个角速率传感器来确定弹体滚转角γ,这样在滚转角已知情况下,来计算偏航角和俯仰角[4-6]。
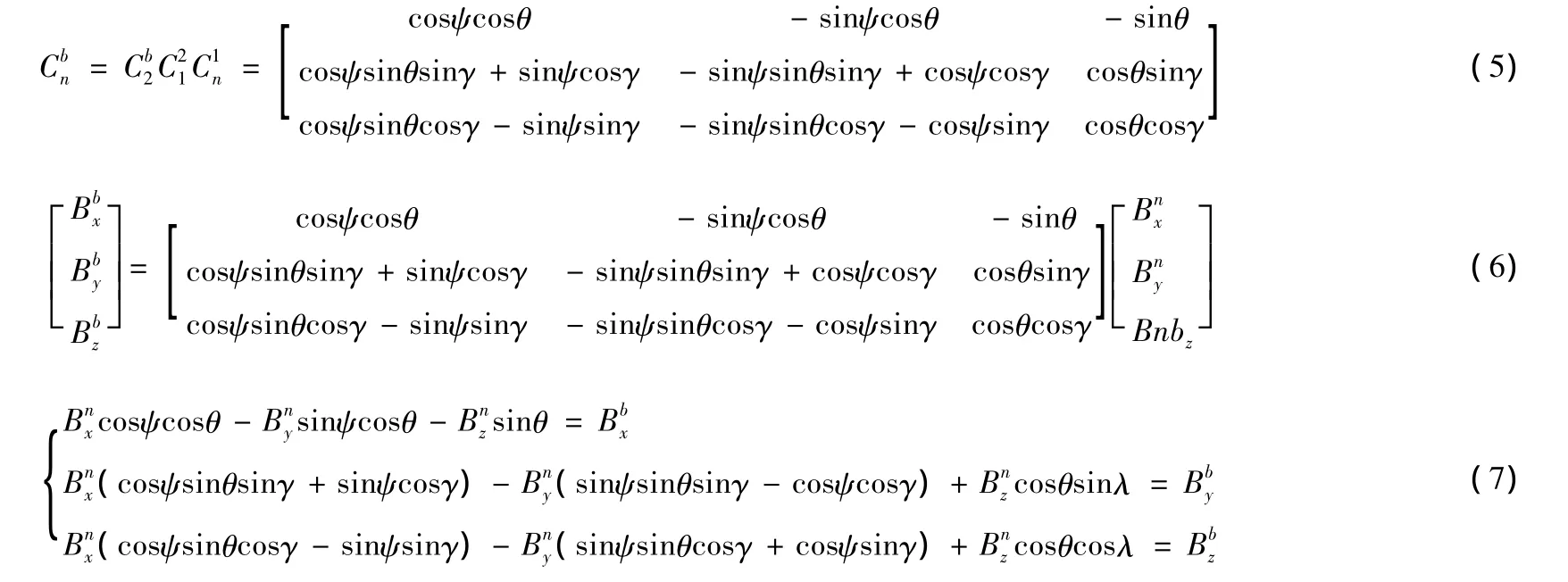
1.3 基于气压传感器的高度测量
制导炸弹的飞行高度在制导控制环节是必不可少参数,虽然可以利用GPS来测量弹体高度,但是在一些封闭(掩体、高架桥下等)环境中,GPS卫星的信号容易被遮挡,导致GPS在垂直方向上的测量精度不高,因而加入气压传感器以提高垂直方向上的制导控制精度。在弹载高度测量方法中,基于气压传感器的数字测量技术应用最为广泛。气压传感器测高的基本原理是根据大气压强随高度变化而变化的关系来测量海拔高度,一般传感器直接感应出来信号的通过敏感元件感测到的压力信号和温度信号,然后利用处理器计算压力、温度与高度的关系式而得到高度值。随着微机电技术与传感器技术的飞速发展与应用,数字式的气压传感器高度集成了感测、处理与温度补偿功能,使用时可以直接运用传感器测出的高度值而不必再额外通过处理器计算,只需简单的外部电路设计即可应用,因此选用气压传感器时一般都偏向于采用数字信号的产品,这种传感器测量范围广,方便移动,可进行绝对高度和相对高度测量[7,8]。
弹载气压传感器测量弹体飞行时高度值,利用气压传感器测量弹体下落过程中不同高度的大气压强和温度,并内部进行温度补偿和计算处理,直接输出弹体实时高度信号,然后通过采集电路将高度信号采集存储,供后续控制弹体姿态时作为参量计算。
2 姿态测量系统设计
本文设计的测量系统是基于弹载GPS和地磁传感器组合来获取相应的参量,其硬件平台按功能机构可划分为不同模块[9,10],如图 4 所示,主要包括主控模块(微处理器)、电源模块、GPS接收模块(接收机+天线)、传感器模块(气压传感器、地磁传感器、角速率传感器),以及通信模块和数据缓存模块组成,微处理器主要通过对量测器件输出量的采集处理,解算出弹体的姿态,并与目标样本参量对比、融合、解算后生成控制指令;GPS接收模块包括弹载GPS接收机和接收天线,提供弹体的实时位置信息,并与目标样本参量对比形成导引弹体飞行的舵控指令;由于GPS高程信息准确度相对较差,因而加入气压传感器来采集弹体所在位置的气压值和温度值,解算输出弹体高度值,主要是辅助提高GPS高程精度;地磁传感器通过敏感轴测得的地磁场,以及角速度陀螺仪测得的弹体滚转角速度,为姿态角的解算提供参量;通信模块构建测量系统和控制系统直接的数据传输通道;数据缓存模块用于对微处理器处理的数据进行实时储存。
在测量器件选型上,以高精度、小体积、低功耗为主要原则,注重器件的高度化集成以减小弹载平台的占用空间,并且满足弹体飞行过程中的测量范围。
测量系统主程序是一个无条件大循环过程,系统上电后,测量系统开始工作。首先进行系统初始化,然后通过多任务调度来实现各个传感器的功能,以分配时间片的形式分时执行程序,不断地采集GPS和各路传感器信号,按照设计的算法进行数据解算,得出弹体的高度、姿态角等参量并储存,最后通过读取注入弹体的目标样本参量,与之前解算出来的参量进行对比分析,计算出需要修正弹体的舵控指令,最终实现整个测量系统的功能要求,如图5所示。

图4 测量系统功能结构框图
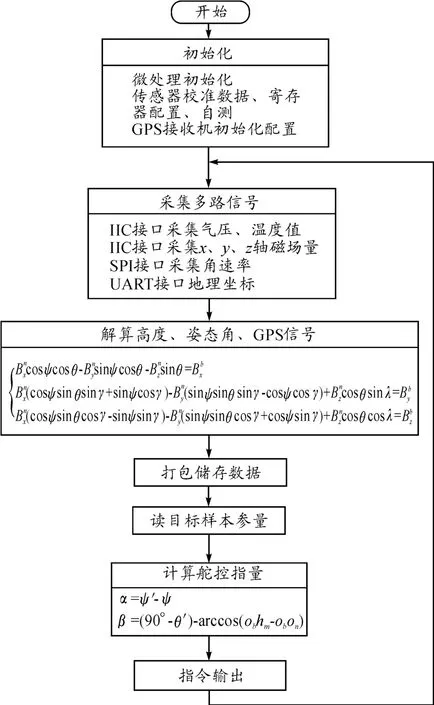
图5 主程序流程
在初始化阶段,系统主要做完成以下工作:①设置微处理器定时器参数,定时时间Tms,中断方式;②将微处理器未使用的引脚设置成上拉电阻输入形式以减小功耗;③ 设置IIC、SPI、UART等串口参数;④ 读取气压传感器校准数据;⑤配置三轴磁场传感器的测量模式、采样平均数、数据传输速率等参数;⑥配置角速率传感器的相关寄存器;⑦初始化化GPS接收机。
完成初始化后,任务调度开始运行,启动定时器工作,以延时中断的形式调用各个子程序运行,系统开始采集各路数据。定义中断int值:
int=0,GPS信号
int=1,气压传感器信号
int=2,地磁传感器信号
int=3,角速率传感器信号
3 结束语
将三轴地磁传感器等搭载至无人机载GPS制导炸弹的微机电测量系统中,用以测量弹体飞行过程中的弹体姿态,经过弹载试验表明,本文提出的方法在一定条件下具备可行性,能够在弹体飞行至5 000~10 000 m(这个地方是不是10 000 m)之间实时修正弹体飞行轨迹,并导引弹体不断向目标逼近,测量结果精度高、可靠性好,满足CEP≤50 m等指标要求。
[1] 周三奇.基于GPS的姿态测量系统研究[D].北京:北京交通大学,2009:11 -19.
[2] 张华强.基于GPS与地磁组合的弹丸姿态解算方法研究[D].南京:南京理工大学,2012:21 -23.
[3] 陶维之.基于磁阻传感器的弹体姿态测量技术研究[D].南京:南京理工大学,2012:10 -14.
[4] 刘晓娜.地磁传感器及其在姿态角测试中的应用研究[D].太原:中北大学,2008:38 -40.
[5] 史震,于秀萍,马澍田.无陀螺捷联式惯性导航系统[M].哈尔滨:哈尔滨工程大学出版社,2005:37-52.
[6] 尹德进,王宏力,刘光斌.捷联惯导系统六加速度计配置方案研究[J].中国惯性技术学报,2003(2):48-51.
[7] 梁胜展,郭雪梅,余晓填.基于BMP085气压传感器及BP算法的高度测量研究与实现[J].传感技术学报,2013(5):654-655.
[8] 马帅旗,史忠科.基于气压传感器的高程测量系统设计[J].测控技术,2010(12):12 -13.
[9] 陈远炫.高精度姿态测量平台的设计与实现[D].广州:华南理工大学,2010:19-24.
[10]杨青,李利锋,范锦彪,等.地磁传感器在弹载测试系统中的应用[J].传感器与微系统,2009(10):108-112.
(责任编辑周江川)

