带炮口制退器的火炮膛口流场三维数值模拟
刘欣宁,岳明凯
(沈阳理工大学装备工程学院,沈阳 110159)
火炮和自动武器发射时会产生大量火药气体,高温高压高速的火药燃气会在膛口附近形成复杂的膛口流场,流场区域内由于火药燃气冲击波的影响而产生有害扰动,如强激波、电磁辐射、膛口焰和膛口烟等等。这些有害扰动非常强烈,不但会暴露阵地,而且会对人员设备造成伤害,同时对射击精度等产生不利影响[1]。为了降低有害扰动对火炮发射的影响,可在火炮膛口加装炮口制退器,以有效降低火炮后坐动能和炮架的射击载荷[2]。因此,如何通过数值模拟的方法对带炮口制退器火炮的膛口流场的形成和发展变化进行仿真,研究炮口冲击现象,减小其对人员设备的影响并提高射击精度是火炮系统研究的重点之一。
早期的相关研究计算主要以实验为主,多采用一维近似算法。进入二十世纪,由于计算机的出现及计算流体力学理论的发展,研究人员开始采用模拟仿真的手段对膛口流场进行研究,但是由于计算机性能的限制,早期的研究对仿真模型多进行较大程度的简化,所得结论并不理想。Cler等[3]分别通过FLUENT软件和DGC代码对不含运动弹丸的膛口流场进行了数值模拟,并将仿真结果与实验阴影进行对比,结果显示在火药气体未喷出之前,计算所得初始流场与实验照片基本相符;而火药气体喷出后,仿真火药气体流场与实验存在出入。Maillie[4]用二维激波捕获法计算了带炮口制退器火炮的膛口流场,为模拟弹丸运动情况,将弹丸在网格中固定令火炮身管以弹丸发射速度向后移动,计算结果显示所采用的格式具有太大的格式粘性,导致膛口冲击波被抹平。
随着大型计算机运算能力的提升,目前对膛口流场的研究逐步向三维、高精度格式、弹丸形状复杂等趋势发展。Sakamoto和 Matsunaga等[5]基于三维可压缩 Euler方程,忽略弹丸的影响,对膛口流场的模拟分析在空间离散上采用Roe方法,在时间离散上釆用3阶 Runge-Kutta法,模拟了膛口冲击波在整个流场的过程。Schmidt等[6,7]研究了炮口制退器的受力情况、炮口冲击波及其传播方向、炮口射流特性等。马大为采用MUSCL差分格式分别计算了有无膛口装置情况下的二维轴对称膛口流场,得到了两种不同情况下膛口流场的参数分布[8]。张焕好、陈志华等人研究了制退器内流场复杂三维瞬态效应的主要特征,并对开腔式制退器的制退效率进行了计算[9]。王仕松,郑坚等在模拟火炮发射过程中的非定常燃气射流流场时,采用分块网格划分的整体运动处理方法和基于动态层变方法的结构动网格技术处理弹丸高速运动造成的网格变化,提高了网格质量和计算速度[10]。
本文应用FLUENT软件,运用结构化动网格技术对弹丸的运动加以处理,建立膛口流场三维数值模型,采用三维非定常Euler方程,使用Roe格式,对某带制退器火炮的膛口流场进行仿真模拟。
1 数值计算方法
由于膛口流场是非定常﹑多相﹑湍流并有方向性和化学反应的复杂流场,因此仿真计算一般都会进行适当的简化。本文在计算之前做了如下简化:流动为准定常等熵流动;火药气体为完全气体,忽略其气体多组分和化学反应的影响;弹丸出膛口后,火药气体射流呈轴对称流动,对称轴为炮口轴线;弹丸从出膛口至后效期为止的过程视为膛口流场模拟全过程。
1.1 控制方程
采用三维非定常Euler方程[11]

其中:ρ为气体密度;u、v、w分别为x、y、z方向上的速度分量;E为总能量,其表达式为
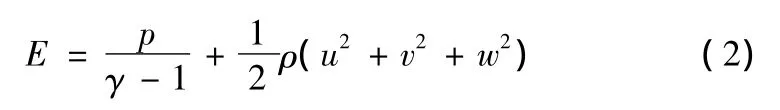
式(2)中γ为理想气体绝热指数。理想气体的状态方程为

式(3)中R为通用气体常数。
1.2 湍流模型
本文使用的湍流模型为单方程(Spalart-Allmaras)模型[12]:
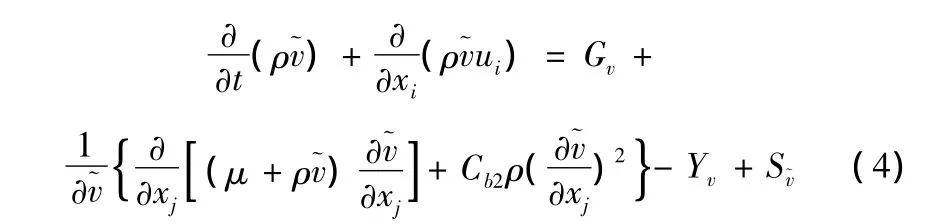
1.3 方程的离散方法
方程的离散采用有限体积法。采用Roe一阶迎风格式将对流项离散为[13]

2 仿真计算模型及网格划分
本文的模拟仿真是在FLUENT软件中进行的,先使用GAMBIT确定几何形状、建立计算模型、划分网格及设定边界条件,然后导入FLUENT中设置具体的边界条件、材料物理属性以及计算模型等,并执行流场的求解。
选用某冲击式炮口制退器为例进行模拟计算,其三维模型及表面网格划分如图1和图2所示,流场计算区域的网格划分情况如图3所示。网格划分在FLUENT前处理软件GAMBIT中进行。为了减少因网格数量过多造成计算量过大,采用分块划分的结构化网格系统,其中静态区域和网格变形区域采用六面体结构化网格,刚体运动区域采用四面体结构化网格。采用动态分层技术生成动网格,用以模拟弹丸飞出炮口后相对炮管的运动过程。

图1 炮口制退器三维模型
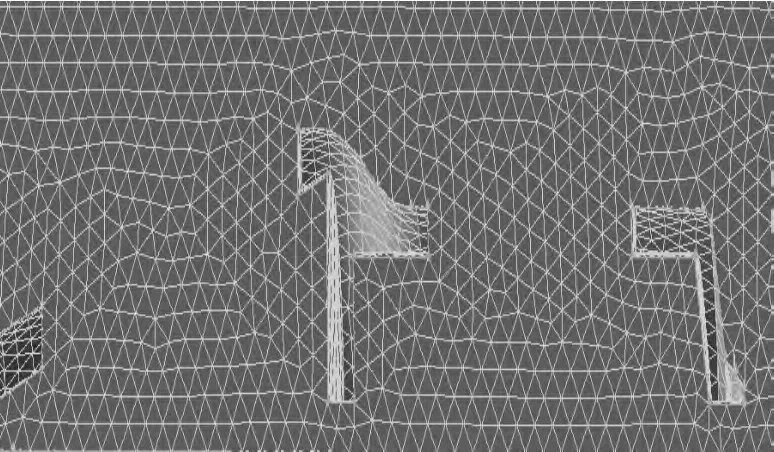
图2 炮口制退器表面网格
考虑弹丸在流场中的运动情况,本文采用结构化网格的动态分层技术,根据相邻运动边界网格层高度的变化,适当增减动态层。该方法的基本思想是:

式(7)、式(8)中:hideal为理想单元高度;αs为网格层的分割因子;αc为网格层的合并因子。
当动边界拉伸毗邻网格层满足式(7)时,可对网格层进行分割;当动边界压缩毗邻网格层满足式(8)时,两网格层将合为一层。该方法模拟过程耗时少,同时结合分块网格技术对炮口流场进行数值模拟。
为了描述膛口处弹丸相对于火炮身管的运动情况,在计算中把整个流场区域划分为静网格区和动网格区,图3中弹丸前后区域为网格变形区,其中前方为网格分裂区,后方为网格合并区,弹丸所处为刚性运动区,而静、动网格区由运动分界面区分开。计算开始后,弹丸以恒定速度沿炮口轴线飞离炮口制退器,动网格相对静网格为滑动,前端网格不断分裂,后端网格不断合并成新网格,以此模拟弹丸的相对运动过程。
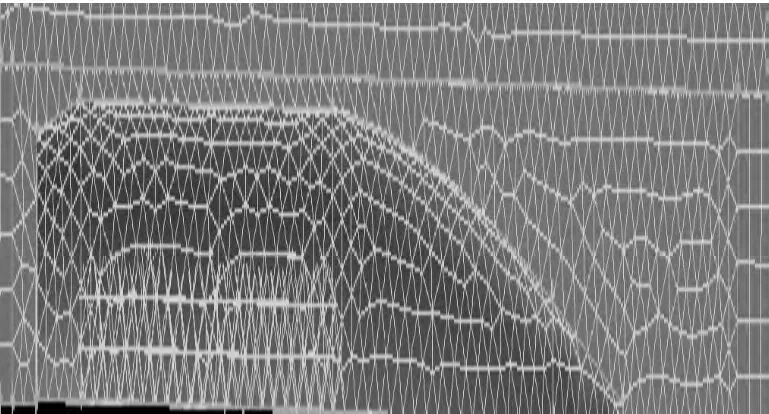
图3 计算区域网格划分情况
3 仿真结果及分析
经三维仿真计算,可得弹丸出膛后膛口流场的发展变化过程。弹丸飞出炮口后,流场的分布及其结构较为复杂。以弹丸飞离炮口瞬间的时刻为界,膛口流场经历了两个阶段的变化,分别为初始流场和火药气体流场。
由于炮口制退器对火药气体的分流作用,使火药气体在喷出炮口后,会在制退器内部形成复杂的流场结构。如图4所示为模拟得到的弹丸出膛后膛口流场在不同时刻发展变化过程的压力云图及等值线图,以及弹丸在膛口流场中的运动变化情况。

图4 不同时刻膛口流场的压力云图
弹丸飞出膛口后,膛内高温高压的火药燃气迅速膨胀流出,进入制退器后继续膨胀。由于炮口制退器的中心孔直径与弹丸直径大小相差较小,所以只有小部分的火药燃气通过弹丸与制退器内壁之间的缝隙,从中心孔流出,大部分的火药燃气则是通过炮口制退器的侧孔流入流场区域(如图4(a)所示)。火药气体推动初始流场空气产生的膛口冲击波首先在弹丸两侧形成,火药气体流动的界面逐渐追上弹丸,弹底压力高于弹尖压力。
弹丸继续沿轴线飞行,火药燃气的流动受到炮口制退器第一对侧孔处挡板的阻挡,会在上下两侧挡板的影响下形成反射激波(见图4(b)),并且在炮口制退器的轴线上膨胀。由于火药燃气与制退器内部反射流场的相互作用,会在制退器内部耦合成一道强激波。
在膛口膨胀的高速火药燃气与制退器内部反射流场的相互作用下,使激波形状发生变化。随着第一对侧孔挡板处反射激波的减弱,膛口高压燃气流的影响逐渐增强,在制退器内高压膨胀使激波变形,并在制退器壁面与强激波间形成二次激波(图4(c))。
弹丸运动到第二队侧孔处,火药燃气受挡板影响形成反射激波,弹底气流膨胀,压力下降(见图4(d))。由于受到高压火药气体的影响,激波在制退器轴向出口处内侧形成斜激波。
弹丸逐渐飞离炮口制退器(如图4(e)、(f)所示),火药燃气分别从炮口制退器的中心孔及两个侧孔向外流出,在流场中不断向四周扩散。制退器侧孔出口处逐渐开始形成复杂的波系结构,并会在持续短暂时间后,最终消失。
图5显示的计算时间内一选定时刻的三维视图,可以更加直观的了解在整个流场区域的压力分布情况。

图5 t=0.3 ms时压力等值线三维分布
4 结束语
膛口流场是包含运动弹丸、强激波、冲击波、电磁辐射等相互作用的复杂流场,流场中流出的高温、高速、高压气体会对火炮炮身和弹丸产生后效作用。加装炮口制退器后,火药燃气流经制退器时会在中央弹孔和各侧孔处分别形成相对独立的火药燃气冲击波和射流,并相互作用合成得到带制退器情况下的膛口冲击波,所以此情况下的膛口流场更为复杂。因此,需要对带制退器的膛口流场进行准确计算分析。
本文基于三维非定常Euler方程,借助Roe格式和结构化网格动态分层技术,同时考虑到炮口制退器对弹丸在膛口流场中运动的影响,对带炮口制退器、含弹丸飞出炮口后在膛口流场的形成、发展过程过程进行了仿真。通过仿真得出以下结论:
1)基于动态分层技术的分块划分网格方法来处理复杂边界的运动情况是可行的,这种方法生成的网格在三维运行环境中质量较高,且运算速度较快,同时可以避免因边界运动而导致网格体积为负的状况出现;
2)虽然计算中有炮口制退器的影响,但是膛口流场仍保留其典型特征不变,在初始流场、火药气体流场和弹丸的相互作用下,仍出现初始激波和膛口冲击波等现象,但火药气体会在制退器内产生高速膨胀,向外扩散时会受到制退器挡板的阻挡,并在制退器内壁面与弹丸相互作用,从而使膛内的波系结构更为复杂。
3)本文忽略了火药燃气化学反应的数值模拟,后续研究可以考虑火药燃气与环境大气之间的热交换,研究二次燃烧对膛口流场的影响。此外,弹丸在含炮口制退器的膛口流场中的数值模拟分析结果,对弹丸以及制退器的结构优化设计有借鉴意义。
通过三维数值模拟分析,可以得出含炮口制退器的膛口流场的形成、发展和衰减的过程,对流场机理研究和制退器的效率计算及结构设计都具有积极的指导意义。
[1] 尤国钊,许厚谦.中间弹道学[M].北京:国防工业出版社,2003.
[2] 高跃飞.火炮反后坐装置设计[M].北京:国防工业出版社,2010.
[3] CLER D L,CHEVAUGEON N,SHEPHARD M S.CFD Application to Gun Muzzle Blast—— a Validation Case Study[C]//41stAerospace Sciences Meeting and Exhibit.AIAA,2003:1142-1147.
[4] MAILLIE F H.Finite difference calculations of the free-air blast field about the muzzle and a simple muzzle brake of a 105mm howitzer[R].Naval Surface Weapons Center,Rept.TR-3002,1973.
[5] SAKAMOTO K,MATSUNAGA K.Numerical analysis of the propagating blast wave in a firing range[J].19th International Symposium of Ballistics,2001:289 -292.
[6] SCHMIDT E,GION E,SHEAR D.Acoustic thermometric measurements of propellant gas temperatures in guns[J].AIAA Journal,1977(15):222 -226.
[7] SCHMIDT E,SHEAR D.Optical measurement of muzzle blast[J].AIAA Journal,1975,13:1086 -1090.
[8] 马大为.含复杂波系的膛口非定常流场的数值模拟[D].南京:南京理工大学,1991.
[9] 张焕好,陈志华,姜孝海,等.膛口装置三维流场的数值模拟及制退效率计算[J].兵工学报,2011,32(5):513-519.
[10]王仕松,郑坚,贾长治,等.带制退器的膛口流场数值模拟[J].火力与指挥控制,2011,36(2):148 -151.
[11]唐家鹏.FLUENT14.0超级学习手册[M].北京:人民邮电出版社,2013.
[12]于勇.FLUENT入门与进阶教程[M].北京:北京理工大学出版社,2008.
[13]张师帅.计算流体动力学及其应用——CFD软件的原理与应用[M].武汉:华中科技大学出版社,2011.
(责任编辑周江川)

