几个易混的条件模型辨析
卞望来
(江苏省南菁高级中学,江苏 江阴 214437)
几个易混的条件模型辨析
卞望来
(江苏省南菁高级中学,江苏江阴214437)
具体情况具体分析是科学思维方法的精髓.在物理问题解决中,各种条件往往对物理过程起到很重要的制约作用,学生在学习中往往不注意分析,常常在解题中不得其法.一根绳子、一根杆、一个斜面,从不同的方向制约了物体的运动,对物理过程形成了一定的约束条件.条件模型就是将巳知条件模型化,剔除条件中的次要因素,突出条件的本质因素,化难为易,为问题的求解铺平道路.以下是中学阶段经常出现但却容易混淆的几个条件物理模型.
1弹簧与细绳
例1:如图1所示,一质量为m的物体系于长度分别为L1、L2的两根细线上,L1的一端悬挂在天花板上,与竖直方向夹角为θ,L2水平拉直,物
体处于平衡状态.现将L2线剪断,求剪断瞬时物体的加速度.
(1) 以下是某同学对该题的解法:设L1线上拉力为T1,L2线上拉力为T2,重力为mg,物体在三力作用下保持平衡,有:T1cosθ=mg,T1sinθ=T2,T2=mgtanθ.剪断线的瞬间,T2突然消失,物体即在T2反方向获得加速度.因为mgtanθ=ma,所以加速度a=gtanθ,方向与T2反向.
你认为这个结果正确吗?请对该解法作出评价并说明理由.
(2) 若将图1中的细线L1改为长度相同、质量不计的轻弹簧,如图2所示,其他条件不变,求解的步骤和结果与(1)完全相同,即a=gtanθ,你认为这个结果正确吗?请说明理由.

解析:(1) 错.因为在L2被剪断的瞬间,L1上的张力大小瞬间发生了变化.物体在重力和L1的拉力作用下运动,因而剪断瞬间物体的加速度为a=gsinθ.
(2) 对.因为L2被剪断的瞬间,弹簧L1的长度来不及发生变化,其弹力大小和方向都不变.
点评:弹簧与细绳产生的弹力属于不同形变范畴产生的,弹簧产生的弹力属于宏观形变产生的,其形变量需要一定时间运动才能改变;细绳产生的弹力属于微小形变量产生的,其形变量可瞬间改变.在教学时,老师要提醒学生注意这两者间的区别,这样学生才能把握这类问题.
2轻杆与细绳
例2:如图3所示,轻杆长L,质量可忽略不计,杆的一端连接着一质量为m的小球,另一端装在固定转轴上.设小球在竖直平面内作圆周运动.(1) 当它在圆周的最低点,速率为v时,求其对杆作用力的大小和方向;(2) 当它在圆周最高点,速率为v时,求其对杆作用力的大小和方向.
解析:小球在竖直平面内作的圆周运动并不是匀速圆周运动.但在最低点和最高点这两个特殊位置,我们仍可用求解匀速圆周运动的方法和公式求解,因为在这两个位置.小球受的外力都在圆周半径方向上,它们沿半径方向上的合力就是向心力.
在最低点:此位置杆对球作用力N的方向只可能向上,并且N>mg,故有:N-mg=mv2/L,N=mg+mv2/L.




3活结与死结
例3:如图4所示,长为5m的细绳的两端分别系于竖立在地面上相距为4m的两杆的上端A、B,绳上挂一个光滑的轻质挂钩,其下连着一个重为12N的物体,平衡时,问:
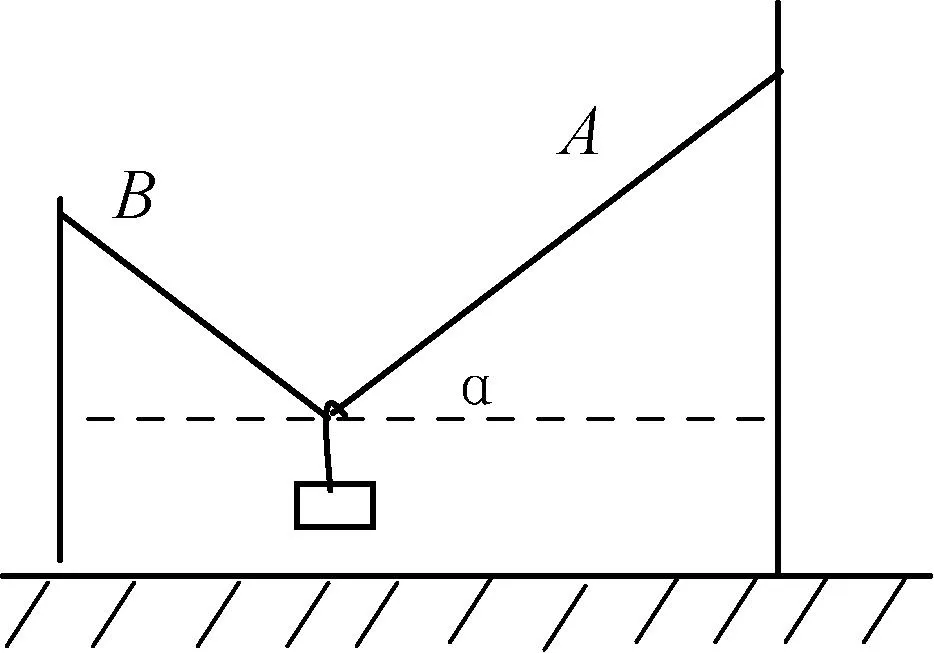
图4
(1) 绳中的张力T为多少?
(2)A点向上移动少许,重新平衡后,绳与水平面夹角,绳中张力如何变化?

图5
解析:(1) 因为是在绳中挂一个轻质挂钩,所以整个绳子处处张力相同.轻质挂钩的受力如图5所示,由平衡条件可知,T1、T2合力与G等大反向,且T1=T2,所以T1sinα+T2sinα=T3=G,即T1=T2=,而AOcosα+BOcosα=CD,所以cosα=0.8,sinα=0.6,T1=T2=10N.
(2) 同理:把A点向上移动少许,重新平衡后,由于绳中挂一个轻质挂钩,整个绳子张力仍相同.由绳子长度与杆之间的距离均不变,可推导绳与水平面夹角保持不变,因而绳中张力保持不变.
例4:如图6所示,AO、BO和CO三根绳子能承受的最大拉力相等,O为结点,OB与竖直方向夹角为θ,悬挂物质量为m.求:
(1)OA、OB、OC三根绳子拉力的大小.
(2) 把A点向上移动少许,重新平衡后,绳中张力如何变化?

解析:(1) 节点O的受力如图7所示,由平衡条件可知,T1、T2合力与G等大反向,但T1不等于T2,所以:T1=T2sinθ,G=T2cosθ.
(2) 把A点向上移动少许,重新平衡后,由于绳OA、OB与竖直方向均发生变化,因而绳OA、OB中的张力均要发生变化.
点评:在例3中绳中挂一个轻质挂钩,钩的两端同属一根绳子,两端绳子的张力相同,简称为活结.在例4中O点是AO、BO和CO三根绳子的结点,它们分属不同的绳子,产生不同的张力,可称为死结.在教学中,老师要指出看上去相似的模型,其实有着本质的不同,关键在于活结与死结的区别.
4活杆与定杆
例5:如图8所示,质量为m的物体用细绳OC悬挂在支架上的O点,轻杆OB可绕B点转动,求细绳OA中张力T和轻杆OB受力N的大小.
解析:由于轻杆OB可绕B点转动,悬挂物体质量为m,绳OC中拉力大小是mg,将重力沿杆OB和细绳OA方向分解,可求得:T=mg/sinθ,N=mgcotθ.

例6:如图9所示,水平横梁一端A插在墙壁内,另一端装有小滑轮B,一轻绳一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量为m=10kg的重物,则滑轮受到绳子作用力为().

解析:由于杆AB不可转动,是定杆,杆所受弹力的方向不沿杆AB方向.由于B点处是滑轮,它只是改变绳中力的方向,并未改变力的大小,滑轮两侧绳上拉力大小均是100N,夹角为120°,故而滑轮受绳子作用力即是其合力,大小为100N,正确答案是C.
点评:在解这2道题时,学生往往不得其法,不入其门,弄不清楚为什么在例5中杆的弹力沿杆的方向,而在例6中杆的弹力不沿杆的方向.例5、例6中的二杆之所以所受弹力方向有这样大的区别,是因为二杆一方面分属活杆与死杆,另一方面也与杆所受外力不同有关,在例5中的绳子为死结,例6中的绳子为活结.
总之,在高中物理教学中,老师不能停留在就事论事上,一定要将物理问题的约束条件说清楚,特别是看似相似的问题,其约束条件的不同要指出来.然后将不同约束条件转化为不同物理模型,让学生知其然知其所以然.,这样我们教学才能收到事半功倍的效果.

