如何确定带电粒子在磁场中运动轨迹的圆心

如何确定带电粒子在磁场中运动轨迹的圆心

翟雪雅

(江苏省泰州中学，江苏泰州225300)

对近几年高考题目的分析，不难看出，带电粒子在磁场中的运动一直是高考考查热点，不但占有的分值较大，而且难度也较大，让很多学生感到非常棘手.怎样画出带电粒子在磁场中的运动轨迹呢？关键是确定带电粒子在磁场中运动的圆心.下面结合例题谈一谈确定圆心的几种方法.

例1在真空条件下，匀强磁场限定在一个圆形区域内，该圆的半径为r，磁感应强度大小为B，方向如图1所示.一个初速大小为v0的带电粒子(m，q)沿磁场区域的直径方向从P点射入磁场，粒子在洛伦兹力的作用下，在磁场中以半径R绕O′点做匀速圆周运动，从Q点射出磁场时，速度大小仍是v0，但速度方向已发生了偏转，设粒子射出磁场时的速度方向与射入磁场时相比偏转了θ角度，请画出带电粒子的运动轨迹并找出圆心O′.

图1

解析：此题是研究带电粒子在磁场中的运动的经典题，对于已知条件的处理我们可以有多种方法，因此解决问题的途径也就有多种.比如我们可以找出确定圆心的三种方法：

方法1：如图1所示，过入射点P和出射点Q作圆O的两条切线，两条切线的交点就是圆心O′.以O′为圆心，以︱PO′︱为半径画弧PQ，即为带电粒子在磁场中运动的轨迹.然后利用相关的几何知识进行相应的求解.

方法2：先过P点作圆O的一条切线，连接PQ并作PQ的中垂线，两条线的交点也是圆心O′，即入射速度方向的垂线和一条弦的中垂线的交点必是圆心.

方法3：入射速度方向的垂线和圆心角∠POQ的角平分线的交点必过圆心O′.

另外，根据已画出的轨迹我们还可以看出带电粒子在有界匀强磁场中的运动轨迹具有对称性，因此我们还可以利用对称性画出带电粒子在磁场中的运动轨迹.如图2所示，带电粒子在单边界磁场中的运动轨迹.从图中可以看出相同带电粒子(不计重力)从同一位置进入磁场区域内经历一段圆弧后离开磁场区域，由于带电粒子进入时的速度方向不同，造成它在磁场中运动的圆弧轨道各有不同，从磁场区域边界射出的方向也不同.

图2

但是轨迹圆心都在速度方向垂线上，从而入射方向和出射方向与边界的夹角相同，即入射角和出射角具有对称性.

图3

例2如图3所示，垂直于纸面向里的有界匀强磁场，MN是磁场的上边界，磁场宽度足够大，磁感应强度B0=1×10-4T.现有一比荷为q/m=2×1011C/kg的正离子以某一速度从P点水平向右射入磁场，已知P点到边界MN的垂直距离d=20cm，不计离子的重力，试求：

(1) 若离子以速度v1=3×106m/s水平射入磁场，求该离子从MN边界射出时的位置到P点的水平距离s.

(2) 若要使离子不从MN边界射出磁场，求离子从P点水平射入的最大速度vm.

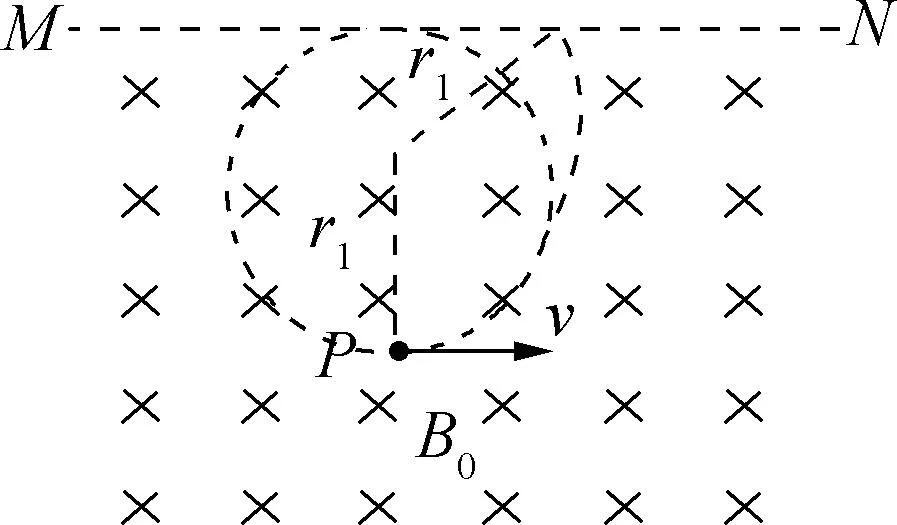
图4

解析：该题主要考查了带电粒子在磁场中的运动，要求能正确画出带电粒子的运动轨迹，并根据几何关系求出半径，能用向心力公式和周期公式进行计算.

(1) 离子在磁场中做匀速圆周运动，由向心力公式可求得轨道半径大小，已知过P点的速度方向和半径大小，圆心的位置可确定，自然可以画出如图4所示的运动轨迹.利用几何关系求解水平位移s.

(2) 由题意，离子刚好不从边界射出的最大半径为r=d/2(如图4)，根据向心力公式可求得最大速度.

例3如图5所示，在第一象限的矩形区域内，有方向垂直于纸面向里的匀强磁场B1，磁场的左边界与y轴重合，第二象限内有互相垂直正交的匀强电场与匀强磁场，其磁感应强度B2=0.5T.一质量m=1×10-14kg，电荷量q=1×10-10C的带正电的粒子以速度v=1×103m/s从x轴上的N点沿与x轴负方向成60°角方向射入第一象限，经P点进入第二象限内沿直线运动，一段时间后，粒子经x轴上的M点并与x轴负方向成60°角的方向飞出，M点坐标为(-0.1，0),N点坐标(0.3，0)，不计粒子重力.求：

(1) 匀强电场的电场强度E的大小与方向；

(2) 匀强磁场的磁感应强度B1的大小；

(3) 匀强磁场B1矩形区域的最小面积.

解析：本题是速度选择器与匀速圆周运动的综合，分析受力情况、确定运动情况是解题的基础,画出轨迹，根据几何知识确定磁场最小区域是解题的关键.

(1) 由已知条件知带电粒子在第二象限内仅受电场力和洛伦兹力，微粒必做匀速直线运动，根据平衡条件，电场力和洛伦兹力大小相等，方向相反，可求出匀强电场的电场强度E的大小与方向.

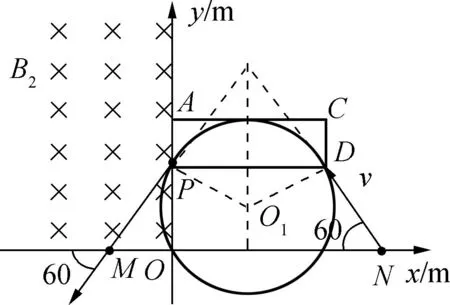
图6

(2) 由已知条件知第一象限内带电粒子仅受洛伦兹力运动轨迹为一段圆弧，根据对称性可判断，圆弧过P点但不过N点.过N点和P点分别作入射方向和出射方向的延长线相交与一点，作夹角的角平分线，角平分线一定过运动轨迹的圆心，在过P点作出射方向的垂线，两条线相交于一点即是带电粒子运动轨迹的圆心O1(如图6).利用几何知识可求得运动轨迹的半径，从而解得B1的大小.

(3) 由图6可知，磁场B1的最小区域应该分布在图示的矩形PACD内由几何关系易得所求磁场的最小面积.

事实上,关于带电粒子(不计重力)在磁场中的运动的题目，解题步骤可概括为“定圆心,画轨迹,根据几何知识求解”.不管考题多么新颖、多么巧妙，关键还是要能够正确地画出带电粒子在匀强磁场中的运动轨迹，而画出运动轨迹,关键在于能确定粒子做圆周运动的圆心.