线性调频信号低旁瓣脉压窗函数的优化设计

时维元，林正英，陈希信

(1. 金陵科技学院 机电工程学院， 南京 211169； 2. 福州大学 机械工程及自动化学院， 福州 350108) (3. 南京电子技术研究所, 南京 210039)



·信号/数据处理·

线性调频信号低旁瓣脉压窗函数的优化设计

时维元1，林正英2，陈希信3

(1. 金陵科技学院 机电工程学院， 南京 211169； 2. 福州大学 机械工程及自动化学院， 福州 350108) (3. 南京电子技术研究所, 南京 210039)

由于线性调频(LFM)信号的幅度谱不是标准的矩形形状，常用的窗函数有时无法将脉压旁瓣降得足够低，因此提出了LFM信号低旁瓣脉压窗函数的优化设计方法。首先，将频域窗函数的求解表示为一个最优化问题，即在保证设计窗函数下的脉压主瓣与期望主瓣的差别小于给定值的条件下，使设计窗函数下的脉压旁瓣尽可能低；然后，将问题表示为标准二阶锥规划形式并求解。仿真实例表明，设计窗的脉压旁瓣显著低于海明窗的脉压旁瓣，设计窗脉压主瓣的无约束部分有所展宽，两个窗函数下脉压信噪比相同。

线性调频信号；脉冲压缩；窗函数；二阶锥规划

0 引 言

线性调频(LFM)信号是雷达中常用的一种脉冲压缩信号，其突出优点是匹配滤波器对目标回波信号的多普勒频率不敏感，大大简化了雷达信号处理系统。但是目标回波信号通过匹配滤波器后的输出具有较高的距离旁瓣(第一旁瓣约13 dB)，因此需要采用加锥削窗的方式来降低旁瓣，代价是分辨率下降和信噪比损失[1]。当LFM信号的时宽带宽积较大时采用目前的窗函数可以将旁瓣降至-40 dB左右，但是难以进一步降低以满足某些实际需要，特别是时宽带宽积较小时-40dB的旁瓣也难以达到。从降低脉压旁瓣的角度来看，常用的锥削窗有时不够理想。文献[2-3]在最小二乘准则下通过迭代搜索方式降低旁瓣，但是迭代系数和收敛性不易控制；文献[4]提出了抑制旁瓣的时域滑窗法，该方法仅适用于脉压旁瓣具有逐点倒相特性的信号，并且旁瓣仍然不能降得很低；文献[5-6]在时域上设计窗函数，获得了令人满意的低旁瓣。实际中LFM信号的脉压经常需要在频域上实现，因此本文采用优化方式在频域上设计窗函数以降低脉压旁瓣，并且考察设计窗下的脉压主瓣展宽和信噪比损失等指标。

1 低旁瓣脉压的优化问题

雷达发射的LFM信号表示为

u(t)=exp(jπγt2), -Tp/2≤t≤Tp/2

(1)

式中：γ=B/Tp为调频斜率，B为带宽，Tp为脉宽。

记u(t)的频谱为U(f)。设距离R0处有一多普勒频率为fD的运动点目标，易知其回波信号的频谱为Ur(f)=a·U(f-fD)·exp(-j2πfτ0)，这里a为回波幅度，τ0=2R0/c，c为光速，则匹配滤波器的输出为

(2)

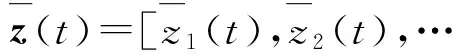
(3)

式中：z(ts)(s=1,2,…,S)是待设计脉压旁瓣，z(tm)(m=1,2,…,M)是待设计脉压主瓣，zd(tm)是期望脉压主瓣；λm为主瓣内不同时间点的误差加权系数，系数越大，设计波瓣与期望波瓣的拟合越接近；ε是设计波瓣偏离期望波瓣的上限，δ对窗函数的范数进行约束，以保证脉压滤波器对随机误差的稳健性；TSL是旁瓣区域上的S个离散时间点的集合，TML是主瓣区域上的M个离散时间点的集合；‖·‖表示范数运算。

式(3)的优化问题是凸的，可以转化成标准的二阶锥(SOC)规划形式，然后利用Matlab的Sedumi工具箱求解[7-8]，下一节将给出详细描述。

2 基于二阶锥规划的窗函数求解

二阶锥规划的对偶标准形式为

(4)

式中：y是包含待求解变量的向量，A是任意矩阵，b和c是任意向量，R是由基本锥(每一个对应一个约束)构成的对称锥集合。A，b和c可以为复数，具有适当的维数。基本锥可以是二阶锥和非负集。

q维二阶锥定义为

SOCq‖x2‖

(5)

式中：R是实数集，C是复数集。

将非负集表示为R+，如果优化问题可以表示成

(6)

则很容易通过Sedumi求出其数值解。式(6)中的对称锥集合表示向量c-ATy的前q1个元素不小于零，后面的q2个元素位于一个二阶锥内。

为了将式(3)的优化问题转化成标准的二阶锥规划形式，首先引入非负变量ξ和εm(m=1,2,…,M)，同时考虑式(2)，我们将式(3)变成

(7)

定义：y=[ξ,ε1,ε2,…,εM,w1,w2,…,wN]T，b=[-1, 01×(M+N)]T，将式(7)中的约束条件写成如下标准形式

y

(8)

m=1,2,…,M

(9)

y，

s=1,2,…,S

(10)

(11)

给定式(1)的LFM信号，期望脉压主瓣zd(tm)，参数ε和δ，以及离散时间点tm(m=1,2,…,M)和ts(s=1,2,…,S)，离散频率点fn(n=1,2,…,N)，代入以上各式，即可应用Sedumi工具箱求解出y，y的最后N个元素构成窗函数w。

3 设计实例与分析

设LFM信号的时宽为10 ms，带宽为20 kHz，采样频率为40 kHz。在优化设计中，采用海明窗的脉压主瓣作为期望主瓣。利用文中方法优化设计窗函数，考察设计窗的脉压旁瓣电平、主瓣展宽和信噪比损失等指标，如图1和图2所示。

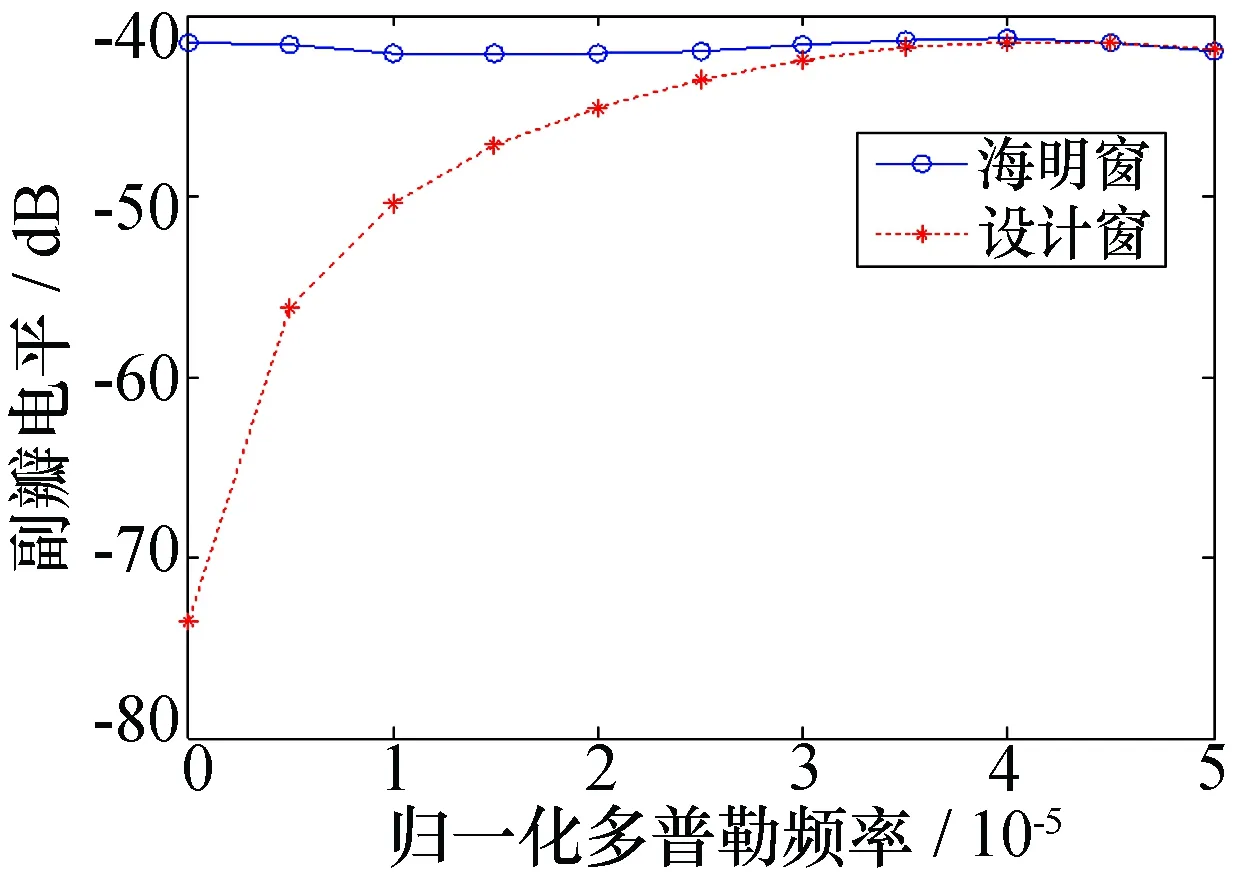
图1 脉压旁瓣电平随多普勒的变化

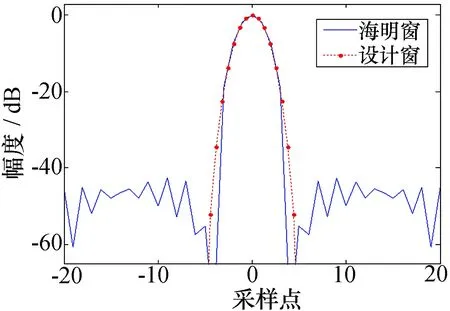
图2 脉压的主瓣

脉压旁瓣电平随多普勒频率的变化如图1所示，多普勒频率为零时约-74 dB，随着多普勒增加，设计窗的脉压旁瓣不断抬高，在归一化多普勒频率(多普勒频率/信号带宽)为0.004时趋近于海明窗的脉压旁瓣，可见设计窗下的脉压对多普勒不敏感，即使多普勒较大，旁瓣电平也不超过海明窗下的旁瓣电平。图2比较了设计窗与海明窗的脉压主瓣，可见-20 dB以上的约束部分两者重合，但是-20 dB以下的无约束部分设计窗脉压主瓣有所展宽，是降低旁瓣而付出的代价。

在LFM信号中添加高斯白噪声，经加窗脉压处理后信号分量和噪声分量分别如图3和图4所示，可见在设计窗和海明窗下两个脉压主瓣高度相同，噪声输出也高度重合，因此两个窗函数下脉压的输出信噪比相同。

图3 脉压后信号的比较

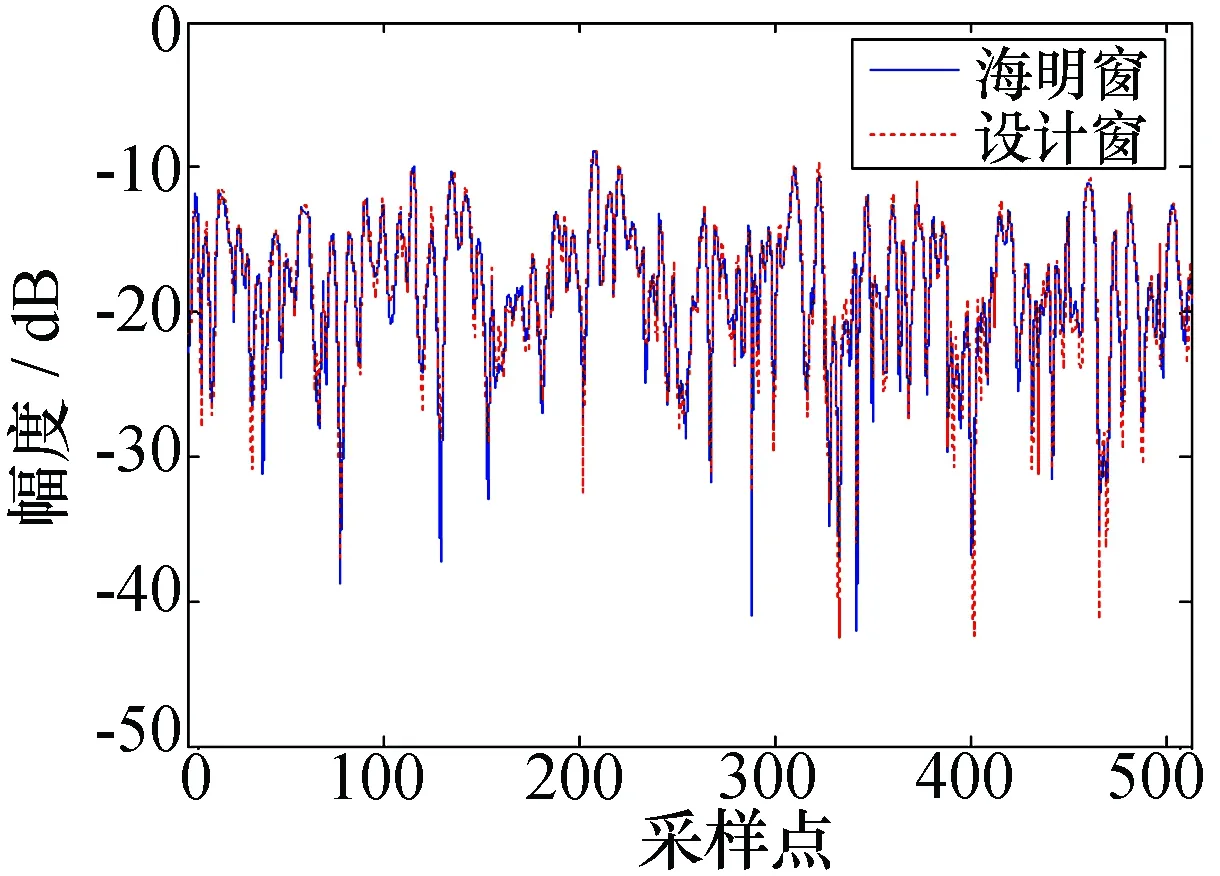
图4 脉压后噪声的比较

4 结束语

常用的窗函数有时无法将脉压旁瓣降得足够低以满足某些实际需要，本文采用优化方式设计窗函数以期进一步降低LFM信号的脉压旁瓣，即在保证设计窗函数下的脉压主瓣与期望主瓣的差别小于给定值的条件下，使设计窗函数下的脉压旁瓣尽可能低。同时，给出了具体的设计实例，并与常用的海明窗比较。结果表明，设计窗的脉压旁瓣显著低于海明窗的脉压旁瓣，两个窗函数下脉压信噪比相同，设计窗脉压主瓣的无约束部分有所展宽，是旁瓣降低的代价。另外，设计窗下的脉压对多普勒频率不敏感，即使多普勒较大，旁瓣电平也不超过海明窗下的旁瓣电平。

[1] 林茂庸, 柯有安. 雷达信号理论[M]. 北京: 国防工业出版社, 1984: 128-130. Lin Maoyong, Ke Youan. Radar signal theory[M]. Beijing: National Defense Industry Press, 1984: 128-130.

[2] Zrnic B M, Zejak A, Petrovic A, et al. Range sidelobe suppression for pulse compression radars utilizing modified RLS algorithm[C]// IEEE Spread Spectrum Techniques and Applications.[S.l.]: IEEE Press, 1998(3): 1008-1010.

[3] 杨 斌, 向敬成, 刘 晟. 一种数字脉压旁瓣抑制滤波器设计方法[J]. 电子科学学刊, 2000, 22(1): 124-129.

Yang Bin, Xiang Jingcheng, Liu Sheng. A method to design digital pulse compression filters for sidelobe suppression[J]. Journal of Electronics, 2000, 22(1): 124-129.

[4] 张砾坪, 彭应宁, 王秀坛. 滑窗式线性调频及衍生多相码旁瓣抑制滤波器[J]. 清华大学学报, 2001, 41(1): 20-23. Zhang Liping, Peng Yingning, Wang Xiutan. Slide-window sidelobe suppression filter for LFM and LFM-derived polyphase coded waveforms[J]. Journal of Tsinghua University, 2001, 41(1): 20-23.

[5] Cilliers J E, Smit J C. Pulse compression sidelobe reduction by minimization of Lp norms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 1238-1247.

[6] 丁淑娟, 刘子龙, 孙广俊. 线性调频信号数字脉压滤波器优化设计[J]. 数据采集与处理, 2012, 27(5): 602-606. Ding Shujuan, Liu Zilong, Sun Guangjun. Digital pulse compression filter optimization design for LFM signal[J]. Journal of Data Acquisition & Processing, 2012, 27(5): 602-606.

[7] Sturm J F. Using Sedumi 1.02, a MATLAB toolbox for optimization over symmetric cones[J]. Optimization Methods and Software, 1999, 11(12): 625-653.

[8] Boyd S, Enberghe L V. Convex optimization[M]. UK: Cambridge University Press, 2008.

时维元 男，1972年生，博士，讲师。研究方向为数字化设计与制造、机电检测与控制。

林正英 女，1968年生，博士，副教授。研究方向为数字化设计与制造、机电检测与控制。

Optimal Design of Window Function for LFM Signal Low-sidelobe Pulse Compression

SHI Weiyuan1，LIN Zhengying2，CHEN Xixin3

(1. College of Mechanical and Electrical Engineering, Jinling Institute of Technology, Nanjing 211169, China) (2. School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350108, China) (3. Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)

The sidelobes of pulse compression (PC) of linear frequency-modulated (LFM) signal sometimes cannot be lowered sufficiently via the usual window functions because the amplitude spectrum of LFM signal is not of the standard rectangular shape. An optimal design approach to the window function of LFM signal low-sidelobe PC is presented in this paper. In this approach the window function making the PC sidelobes as low as possible is found via the standard second-order cone programming under the constraint that the difference between the PC mainlobe of designed window and that of the desired window is less than some given value. The simulation example shows that the PC sidelobes of designed window are remarkably lower than those of Hamming window, the constrained part of PC mainlobe of designed window is widened, and the PC SNRs of two window functions are almost same.

linear frequency-modulated signal; pulse compression; window function; second-order cone programming

10.16592/ j.cnki.1004-7859.2015.10.005

金陵科技学院科研基金资助项目(40610049)

时维元 Email：shiweiyuan@jit.edu.cn

2015-06-27

2015-09-08

TN957

A

1004-7859(2015)10-0018-03