一种对MIMO雷达正交QPSK信号的参数估计方法

李昀豪，王 佩，唐 斌

(电子科技大学 电子工程学院, 成都 611731)



·信号/数据处理·

一种对MIMO雷达正交QPSK信号的参数估计方法

李昀豪，王 佩，唐 斌

(电子科技大学 电子工程学院, 成都 611731)

针对多输入多输出雷达所采用的正交四相编码信号，提出了基于循环自相关函数的参数估计方法。文中首先对正交四相编码信号模型的循环自相关函数和循环谱密度函数进行了推导；然后，依据推导结果，通过对循环谱密度函数最大模值位置的搜索完成了对信号载频的估计；最后，对不同延时条件下循环自相关函数在相位修正后进行累积，实现了对码速率的估计。仿真表明，文中算法在信噪比优于1 dB后，可以较好地完成对正交四相编码信号的调制参数估计。

正交四相编码信号；参数估计；循环自相关；MIMO雷达

0 引 言

近年来，多输入多输出(multiple input multipl output Radar, MIMO) 雷达系统由于其具有灵活的结构、良好的动目标和弱目标检测能力、低截获概率的信号等优势受到了诸多学者的广泛关注[1-2]。MIMO雷达系统为在接收天线中对雷达回波信号进行正交处理，要求其所发射的信号由多个相互正交的信号组成，每个正交信号经过频域或者编码域的正交调制后[3]，由各自对应的发射天线向监视空域发射。因此，区别于传统单载波雷达信号，电子侦察接收机所接收到的MIMO雷达信号由多个相互正交的信号组成，对这类信号的参数估计算法亟待研究。

MIMO雷达研究的初期，四相编码(quadrature phase shift keying，QPSK)信号由于其良好的匹配滤波主副比、灵活多变的码元序列等优势，被学者们引入作为MIMO雷达的发射信号，每个发射天线采用与其他天线信号正交的QPSK信号，即正交QPSK信号。国内外学者对正交QPSK编码信号波形设计的研究使得其编码序列已经能够较好地满足不同天线发射信号间良好正交性的要求[4-6]，本文所研究的主要内容就是针对这一信号的参数估计方法。

国内外针对MIMO雷达信号的电子侦察研究都不完善，文献[7]提出了基于机载平台侦察接收机的MIMO雷达载波数估计方法，该方法通过在空间上的多处采样，得到秩等于载波数的导向矩阵；文献[8]依据多载波信号的高阶统计性质，完成了对多不同MIMO雷达信号的调制类型识别。文献[9]以多天线侦察接收机为背景，研究了对MIMO雷达信号的检测及载波数估计算法。针对正交QPSK信号调制参数估计算法的研究目前尚未见于公开文献。

基于循环自相关函数能体现信号的周期调制特性，文献[10-11]分别提出了基于循环自相关的正弦调频信号和锯齿波线性调频连续波信号的参数估计算法。本文依据正交QPSK信号相位调制点周期性出现这一特性，对其循环自相关函数及循环谱密度函数进行了推导，提出针对正交QPSK信号载频和码速率的估计方法。

1 信号模型

在采用正交QPSK信号的共址MIMO雷达系统[1,3]中，第m个天线所发射的四相编码信号可如下表示[4,6]

(1)

其中

(2)

式中：t∈[t,T),T为脉冲长度；m=0,1,…,M-1，M为MIMO雷达发射天线数；Tc为各编码码元长度，L代表子脉冲个数，TcL=T；编码信息由φm(l)表示，φm(l)∈{0,0.5 π, π, 1.5 π}。假设侦察接收机使用单天线进行侦收，所截获的正交QPSK信号具有如下形式

(3)

式中：b为接收到的信号幅度；θm为各子正交信号间的相位差，这个相位差值由MIMO雷达与以T接收机相对位置及MIMO雷达阵列结构[12]所决定。式(3)表明s(t)由多个载频相同、编码序列及初相不同的QPSK信号组成。

在正交QPSK信号进行波形设计时，最重要的准则是设计能使各天线发射信号的自相关旁瓣峰值及不同天线发射信号的互相关峰值最小化的正交编码序列[3,13]。当子脉冲个数L足够长时，上述要求并不苛刻，所以在完成波形设计后，自相关旁瓣峰值及互相关峰值都远小于自相关主瓣峰值，对信号进行整体分析时可认为下式成立

(4)

对正交QPSK信号参数估计的目标为获得对信号载频f0和码速率fc=1/Tc这两个调制参数的估计。

2 参数估计算法原理

2.1 正交QPSK信号循环自相关函数

对无限长时间连续信号x(t)的循环相关函数定义为[14]

(5)

对于脉冲长度为Tp的正交QPSK信号，其循环自相关函数可通过下式计算

(6)

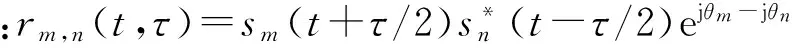
所有数据录入SPSS20.0统计学软件。计数资料以相对数表示，χ2检验。以P＜0.05，为差异有统计学意义。

(7)

uk(t-τ/2)ejφm(l)-jφm(k)-j2παtdt

(8)

结合各QPSK信号自相关旁瓣峰值远小于其主瓣峰值这一特点，不难推导出

(9)

(10)

图1及本节后续仿真中，发射天线数为4，信号载频及码速率分别为20 MHz和5 MHz，离散采样频率为100 MHz，SNR为10 dB。信号能量定义为各天线信号能量之和，即SNR为

(11)

图1 ||仿真结果

2.2 载波频率f0估计

(12)

图(τ)数据选择仿真

(13)

于是通过式(13)可以得到载频f0的估计值，任意信号x(t)的循环谱密度函数定义为[14]

(14)

(15)

(16)

图3 ||仿真结果

(17)

2.3 码速率fc估计

结合式(7)和式(9)，正交QPSK信号的循环自相关函数可近似为

(18)

(19)

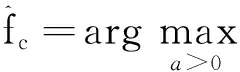
(20)

3 算法仿真

为验证本文算法的有效性，采用两组不同参数的正交QPSK信号(表1)，即sa和sb进行计算机仿真。

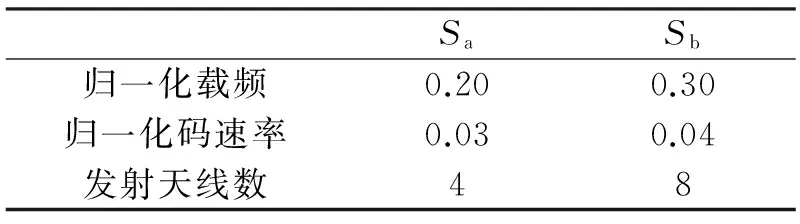
表1 仿真信号调制参数

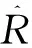
图4 f0估计归一化均方根误差

图4表示，对两组参数的正交QPSK信号的载频估计的NRMSE，都在有SNR优于1 dB后稳定在-22 dB左右，其差别小于1 dB。由此可见，本文算法在估计信号载频时，受不同调制参数影响很小。

图5 fc估计归一化均方根误差

对码速率fc的参数估计误差变化规律类似于对载频fc的估计结果，在SNR优于1 dB后其NRMSE开始稳定。稳定后对两信号fc估计的NRMSE差距在2 dB内，这是由于Sb码速率较大，包含更多的码元信息。

综上，本文算法能较好地完成对正交QPSK信号的载频及码速率估计。

4 结束语

为在单通道电子侦察接收机中完成对MIMO雷达所采用的正交QPSK编码的调制参数估计，本文分析了正交QPSK编码信号的循环自相关函数和循环谱密度函数特点。搜索循环谱密度函数最大模值点，得到信号载频的估计，并在对不同延时值对应的循环自相关函数进行累积时，使用估计到的载频值进行相位补偿，完成对码速率的估计。仿真表明，信噪比优于1 dB时，文中算法能够对不同调制参数的QPSK编码信号进行较精确的调制参数估计。

[1] Li Jian, Stoica P. MIMO radar signal processing[M]. New Jersey ：John Wiley & Sons Inc., 2008.

[2] Wang P, Li H B, Himed Braham. Moving target detection using distributed MIMO radar in clutter with nonhomogeneous power[J]. IEEE Transactions on Signal Processing, 2011, 59 (10), 4809-4820.

[3] 刘 波. MIMO雷达正交波形设计及信号处理研究[D]. 成都: 电子科技大学, 2008. Liu Bo. Research on generation of orthogonal waveform and signal processing for MIMO radar[D]. Chengdu: University of Electronic Science and Technology of China, 2008.

[4] Sharma G V K, Rajeswari K R. Four-phase orthogonal code design for MIMO radar systems[C]// National Conference on Communications (NCC). [S.l.]: IEEE Press, 2012.

[5] Deng H. Poly-phase code design for orthogonal netted radar system[J]. 2004 IEEE Transactions on Signal Processing, 2004, 52(11), 3126-3135.

[6] Liu B, et al. Poly phase orthogonal code design for MIMO radar systems[C]// Internal Conference Radar. [S.l.]: IEEE Press, 2006.

[7] Tang Xiaowei, Tang Jun, Tang Bo, et al. A new electronic reconnaissance technology for MIMO radar[C]// Proceedings of the IEEE CIE International Conference on Radar. [S.l.]: IEEE Press, 2011.

[8] Wang Xiongjing, Xiong Ying, Li Yunhao. Modulation recognition of MIMO radar signal based on joint HOS and SNR algorithm[J]. 2014 Journal of Systems Engineering and Electronics, 2014, 25 (2): 226-236.

[9] Howard S, Sirianunpiboon S, Cochran D. Detection and characterization of MIMO radar signals[C]// International Conference on Radar. [S.l.]: IEEE Press, 2013: 330-334.

[10] 黄 浩，李昀豪，祝 俊. 基于循环自相关的正弦调频信号参数估计新方法[J]. 电讯技术, 2013, 53(9): 1180-1185. Huang Hao, Li Yunhao, Zhu Jun. A new sinusoidal FM signal parameters estimation algorithm based on cyclic autocorrelation[J]. Telecommunication Engineering, 2013, 53(9): 1180-1185.

[11] 朱文涛, 郑纪彬, 苏 涛,等. 锯齿波线性调频连续波信号的检测与参数估计[J]. 西安: 西安电子科技大学学报, 2013, 40(2): 135-142. Zhu Wentao, Zheng Jibin, Su Tao, et al. Detection and parameter estimation of sawtooth linear frequency modulation continuous wave signal[J]. Xi′an: Journal of Xidian University, 2013,40(2): 135-142.

[12] 彭珍妮, 贲 德, 张 弓. MIMO雷达的最小冗余线性阵列配置与优化[J]. 现代雷达, 2014, 36(6): 22-25. Peng Zhenni, Ben De, Zhang Gong. Using minimum redundancy linear array of MIMO radar array optimization[J]. Modern Radar, 2014, 36(6): 22-25.

[13] 李宏伟. MIMO雷达波形设计方法综述[J]. 现代雷达, 2013, 35(6): 12-14. Li Hongwei. Overview of waveform design methods for MIMO radar[J]. Modern Radar, 2013, 35(6): 12-24.

[14] 张贤达, 保 铮. 非平稳信号分析与处理[M]. 北京：国防工业出版社, 1998: 324-326. Zhang Xianda, Bao Zheng. Signal analysis and process of non-stationary signal[M]. Beijing: National Defense Industry Press, 1998: 324-326.

李昀豪 男，1987年生，博士。研究方向为数字信号处理，电子侦察等。

A Method of Parameters Estimation for MIMO Radar Orthogonal QPSK Signal

LI Yunhao，WANG Pei，TANG Bin

(School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

Based on cyclic autocorrelation, a method of parameters estimation for orthogonal QPSK signal used by MIMO radar is proposed in this paper. Firstly, cyclic autocorrelation function and cyclic spectrum density of orthogonal QPSK signal are deduced. According to the deduction, estimation of carrier frequency is accomplished through searching the cyclic spectrum density for the location of the maximal value. Then, cyclic autocorrelation functions of different time delay are accumulated to complete estimation of code frequency. Simulation results verify that the proposed method could achieve accurate parameters estimation when SNR is better than 1 dB.

orthogonal QPSK signal; parameters estimation; cyclic autocorrelation; MIMO radar

10.16592/ j.cnki.1004-7859.2015.10.008

国家自然科学基金资助项目(61172116)

李昀豪 Email：kalec_li@sina.com

2015-06-22

2015-09-01

TN957

A

1004-7859(2015)10-0029-05