无杆飞机牵引车夹持举升机构的运动学分析
王立文,吴志恒,张威,3
(1.中国民航大学地面特种设备研究基地,天津300300;2.中国民航大学航空自动化学院,天津300300;3.中国民航大学机场学院,天津 300300)
0 前言
飞机牵引车是一种通过外加动力移动飞机的地面特种保障设备,它具有“车身低矮、车辆自重较大、牵引力大”等特点[1]。飞机牵引车分为有杆牵引车和无杆牵引车。同有杆牵引车相比,无杆飞机牵引车借助了飞机的部分质量来增加牵引车车轮与地面附着力,达到对牵引飞机的牵引力和制动力的要求,其车身低矮,车辆自重小,更加灵活、安全、高效[2-4]。夹持举升机构是无杆飞机牵引车与飞机直接相连的部分,是飞机牵引车的关键机构之一[5]。飞机与无杆牵引车对接时,通过液压缸的提升与伸出动作,使得飞机前轮进入夹持举升机构并带动相关装置将前轮抱紧并抬离地面100~150 mm,该机构不仅承受前轮承载的飞机质量,传递轴向力及侧向力,还可以保持一定范围内的回转自由度[3,5-7]。
本文作者利用Kutzbach-Grübler公式分析了市面上常用两种夹持举升机构的自由度,并利用机器人学相关知识,计算位姿矩阵,进行相关的速度分析,为理论创新提供了依据。
1 夹持举升机构
夹持举升机构分为夹持机构和举升机构。夹持机构可分为4种类型,分别是回转夹持式、非对称轨道式、对称轨道式、轨道弹簧式[3]。市面上常用的两种为回转夹持式 (图1)和对称轨道式 (图2)。文中据此计算两种夹持举升机构的自由度以及正向运动学分析。

图1 回转夹持式

图2 对称轨道式
2 运动学分析
2.1 回转夹持式
2.1.1 自由度的计算
根据图1所示机构画出回转夹持式的机构简图如图3所示。
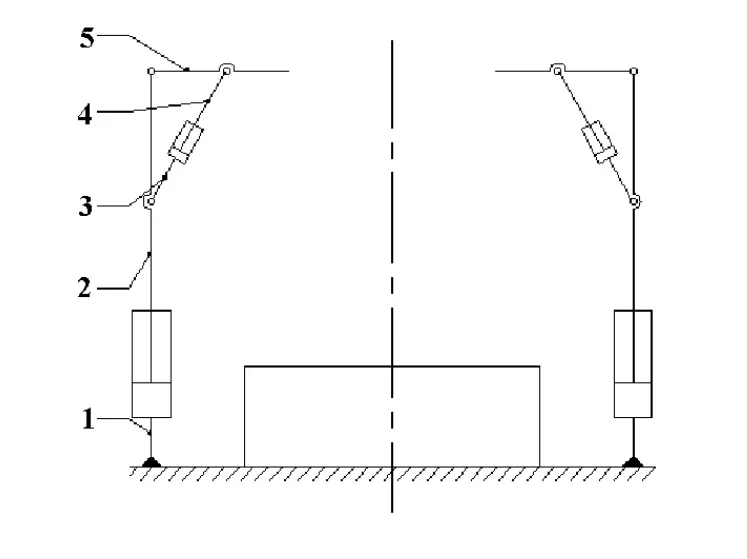
图3 回转夹持式机构简图
由于机构整体是一个完全对称结构,则自由度的计算只考虑一边即可。根据Kutzbach-Grübler公式M=∑fi+3(n-g-1)[8],fi表示第i个运动副的相对自由度数,n为构件数,g为运动副数。图中有5个构件,5个运动副,每个运动副都只含有一个自由度,故机构的自由度数M1=5+3×(5-5-1)=2,与机构简图中主动件数相同,所以符合条件。
2.1.2 齐次坐标的变换
利用Denavit-Hartenberg法建立回转夹持机构的坐标系如图4所示。

图4 回转夹持式D-H坐标
将初始坐标原点建立在飞机前轮中心的位置,设飞机前轮的外径为r,各点的距离如图所示。坐标变换矩阵包含4个,分别为:

手部位姿矩阵可以用如下矩阵来表达:
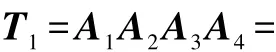

2.1.3 速度分析
回转夹持臂的手部坐标 (x,y)相对于各关节变量有

求偏微分有
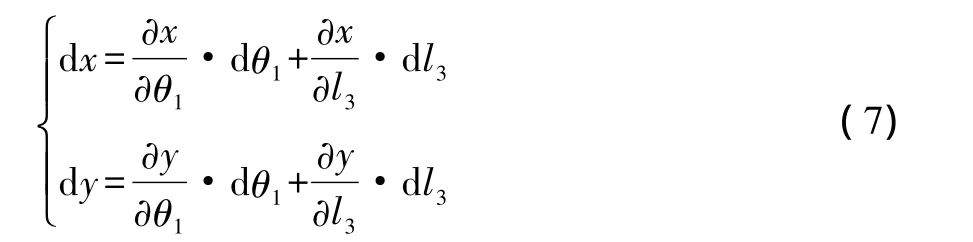
将其写为矩阵形式有
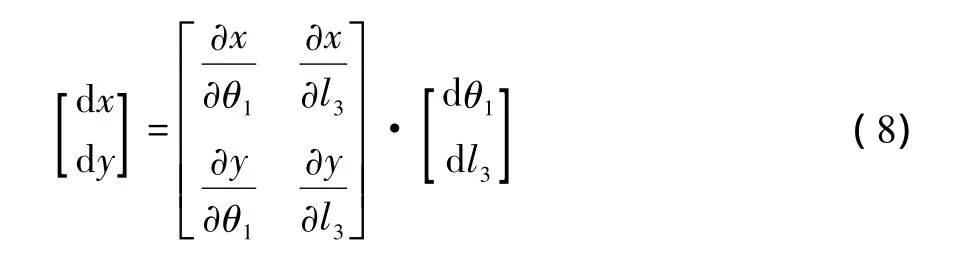
令


将式子两边同时除以dt,得

式中:v为机器人末端在操作空间中的广义速度,v=;J(q)为速度雅克比矩阵;为机器人关节在关节空间中的关节速度。
则手部速度为

2.2 对称轨道式
2.2.1 自由度的计算
根据图2所示机构画出对称轨道式的机构简图如图5所示。

图5 对称轨道式机构简图
由于机构整体是一个完全对称结构,则自由度的计算只考虑一边即可。根据Kutzbach-Grübler公式M=∑fi+3(n-g-1)[8],fi表示第i个运动副的相对自由度数,n为构件数,g为运动副数。图中有5个构件,5个运动副,每个运动副都只含有一个自由度,故机构的自由度数M2=5+3×(5-5-1)=2,与机构简图中主动件数相同,所以符合条件。
2.2.2 齐次坐标的变换
利用Denavit-Hartenberg法建立回转夹持机构的坐标系如图6所示。

图6 对称轨道式D-H坐标
将初始坐标原点建立在飞机前轮中心的位置,设飞机前轮的外径为r,各点的距离如图6所示。坐标变换矩阵包含4个,分别为:
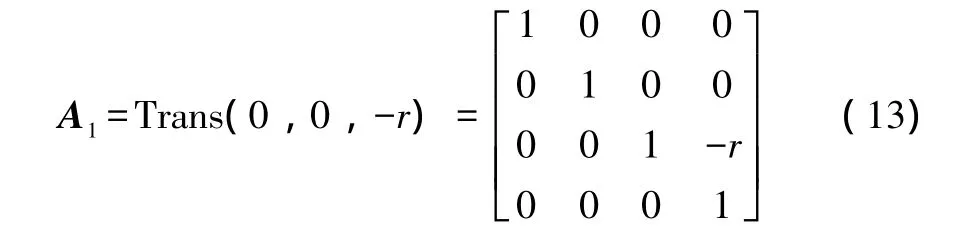

可以得到手部坐标相对于各关节变量的方程:

2.2.3 速度分析
根据公式 (9)得出对称轨道式手臂的速度雅可比矩阵

则手部速度为


图7 回转臂三维模型
3 仿真分析
建立回转夹持式的回转臂三维模型,利用Motion进行仿真,并将仿真结果同理论结果相对比,得出手臂位置的两个方向的运动。
图7给出回转臂的三维模型。
图8给出θ1的速度变化曲线。图9给出l3的速度变化曲线。

图8 θ1的角速度
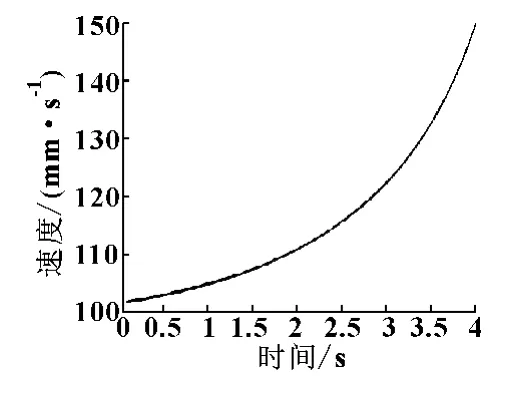
图9 l3速度
设l3的初始长度为1 921 mm,θ1的初始角度为33.6°。由公式 (12)可以分别算出x方向及y方向的速度,如图10、11所示。

图10 回转臂x方向的速度
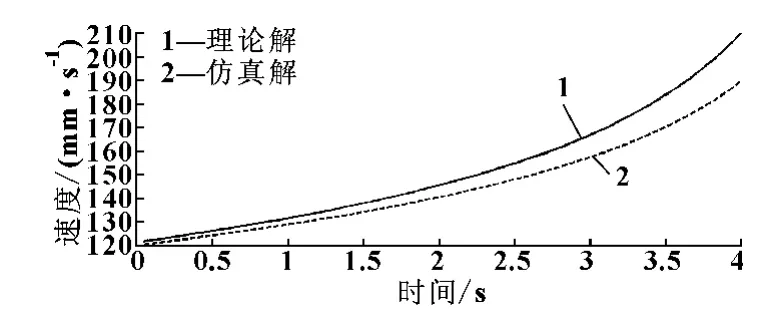
图11 回转臂y方向的速度
根据图10和图11可知,基于D-H变换矩阵的数学模型同三维实体模型计算结果逼近程度较高,x方向的速度最大误差不超过3 mm/s,y方向速度最大误差不超过15 mm/s。通过数学模型得到的理论公式可以较为正确的得出实体模型的实际运动。
4 结论
(1)以D-H变换矩阵为建模工具所建立的运动学模型较为精确,可以得到其正向运动学方程及飞机机轮中心同坐标原点的理论位置变化关系。
(2)利用Solidworks对夹持举升机构进行了三维实体建模并进行运动学仿真,将理论速度计算公式输入到Matlab中并代入各参数,将所求得理论解与仿真结果进行对比。由结果可以看出二者结果逼近程度很高,文中的理论公式及推导以及三维模型的建立均是正确的,为进一步的动力学分析提供了理论基础。
[1]任文轶.浅析有杆式和无杆式飞机牵引车[J].江苏航空,2007(2):25-27.
[2]王志,包小光,齐向阳,等.新型无杆飞机牵引车总体设计[J].起重运输机械,2006(1):27-29.
[3]洪振宇,许致华.无杆飞机牵引车机轮夹持举升机构[J].起重运输机械,2012(4):13-15.
[4]ZHAO Wenzhi.System Analysis of Towing Aircrafts for Taxiing Out[C].2012 International Conference on Information Management,Innovation Management and Industrial Engineering,2012:303-306.
[5]张积洪,李国勇.基于Pro/Engineer的飞机牵引车夹持机构的运动仿真[J].起重运输机械,2008(4):46-49.
[6]毛小馨,刘贵明.基于SolidWorks的无杆飞机牵引车驱动桥结构设计仿真分析[J].机械设计,2010(2):67-70.
[7]许致华,焦永涛,洪振宇.新型无杆飞机牵引车夹持机构[J].起重运输机械,2012(1):76-80.
[8]黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.

