往复走丝线切割电极丝恒张力控制系统研究

陆程，时伟

(中州大学工程技术学院，河南郑州 450015)

0 前言

电火花线切割加工为一种非接触式热蚀除电加工方式，适合加工各种硬度导电材料，由于其具有较高精度、效率、能够加工复杂异面零件等优良特性［1］，广泛应用于模具、仪器、汽车、航空航天等高端制造领域。随着现代制造业对零件的精度和质量要求越来越高，提高加工设备的性能迫在眉睫。针对此情况，许多研究人员做了大量的研究，丁红珍等［2］提出改进电极丝贮丝系统步进电机的方法来提高加工形位误差和表面粗糙度;楼月明、杨蕾等人［3－4］从加工参数角度出发，采用优化算法，从而获取更高的材料去除率和表面质量，狄士春、尚婕等［5－6］研究高性能的高频脉冲电源，采用新的设计思路，优化脉冲电源的设计来提高线切割加工的性能。上述研究在一定程度上减少了加工零件的形位误差，提高表面加工质量。

在往复走丝方式的线切割加工过程中，电极丝张紧力对于电极丝的运动特性影响最大，且难以被实时精确的控制，导致电极丝发生较大的挠曲变形和振动，严重影响加工的效率、精度和稳定性，具体表现在工件表面条纹、形位误差和切口宽度等，因此开发一个能够控制电极丝张紧力的系统很有必要。本文作者提出一种新的中速线切割电极丝往复走丝的走丝方式，引进伺服电机、张力马达和张紧力传感器等，采用自适应控制算法，开发一套闭环往复走丝电极丝恒张紧力控制系统，能够实时的测量电极丝张紧力，并与设置的张紧力进行比较，智能补偿其大小，系统响应速度5 ms，张紧力调整时间在1 s以内。大量的实验数据加工显示，该闭环控制系统对电极丝张紧力的控制效果显著，有效地减少了电极丝换向传输的张紧力波动，且明显减少电极丝运转时产生的挠曲变形和振动现象。

1 电极丝受力分析

在电火花线切割加工过程中，电极丝受力非常复杂，可以分为宏观力和微观力。宏观力主要为电极丝张紧力，微观力主要分为:脉冲放电力、静电力、电磁力和流体黏性力等［7］。本部分对电极丝进行受力分析，如图1所示。

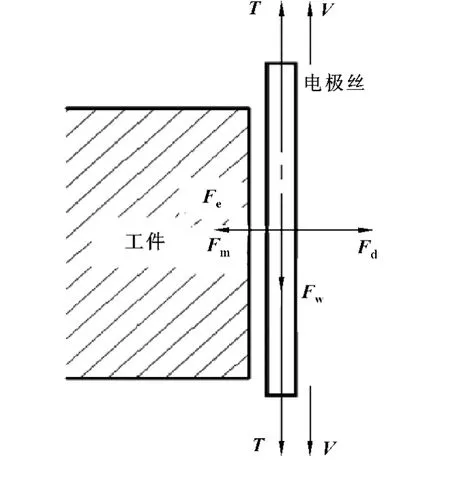
图1 电极丝受力分析示意图

张紧力 (T)是为了使电极丝顺利地在丝筒和导轮之间往复运转，使得导轮之间的电极丝在加工过程中尽量保持为直线，人为的给电极丝增加一个预紧力，其方向如图1所示，其幅值的数量级为10 N。脉冲放电力 (Fd)为加工中，由于电极丝和工件之间的高势差，引起强烈的火花超高温热物理蚀除过程，工件表面的材料在短时间内被熔化、汽化、冲刷走或者再结晶;与此同时，电解液中的泡沫被破裂，许多专家将此类力的合力称为脉冲放电力，该力难被精确测量，其幅值的数量级为10－3N/J［8］，方向与加工进给方向相反。静电力 (Fe)是在脉冲放电间隙中，由于电极丝和工件之间的电势之差，产生一种相互吸引的作用力，对电火花加工电极丝运动特性影响不大。电磁力 (Fm)是由于脉冲电流通过电极丝，在阴极与阳极之间产生电磁感应现象，从而产生相互的电磁力，其幅值的数量级0.01 N/m。流体黏性力(Fd)为电极丝与高速冲击的电解液之间黏性力，其大小跟电极丝传输速度、电解液黏度系数、电解液压力和脉冲放电通道的宽度相关，方向与张紧力方向一致，但幅值远小于张紧力。

2 电极丝张紧力变化原因及其引起的问题

在一般的往复走丝线切割加工中，电极丝的张紧力在8～12 N范围内波动，这个幅度的波动将会对高精度高效率的中速电火花加工造成致命的影响。引起张紧力变化主要由以下3个方面的原因:

(1)丝筒和导轮等机械结构的振动;

(2)电极丝由于放电加工的腐蚀变得更细长;(3)电极丝在传输换向过程中张紧力波动;

较大幅值的张紧力波动严重制约线切割加工的高性能发展，其负面影响主要体现在以下几个方面:

(1)直接影响:导致电极丝产生较大的挠曲变形和振动，挠曲变形分为导轮处和导轮间的挠曲变形［10－11］，图2为电极丝导轮之间的挠曲变形图，公式 (1)为电极丝弦振动方程。

图2 电极丝受合力作用下的挠曲变形

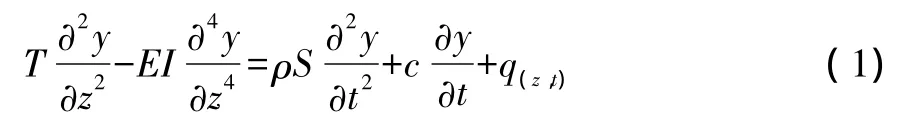
式中:T为张紧力，N;E为弹性模量，N/m2;I为惯性矩，m4;S为横截面积，m2;c为阻尼系数，Ns/m2;q(z，t)为均布脉冲放电力，N/m。当张紧力发生较大波动时，根据弦振动方程，电极丝的运动特性将发生较大的变化，甚至可能出现共振现象。

(2)间接影响

在电火花加工中，控制系统的插补精度和电极丝的运动特性决定加工零件的形位精度，主要体现在拐角误差、切口宽度和上下异性加工面，图3为加工拐角误差示意图;放电蚀除机制、电极丝运动特性共同决定加工零件的表面质量，主要体现在表面粗糙度、表面条纹和裂纹。

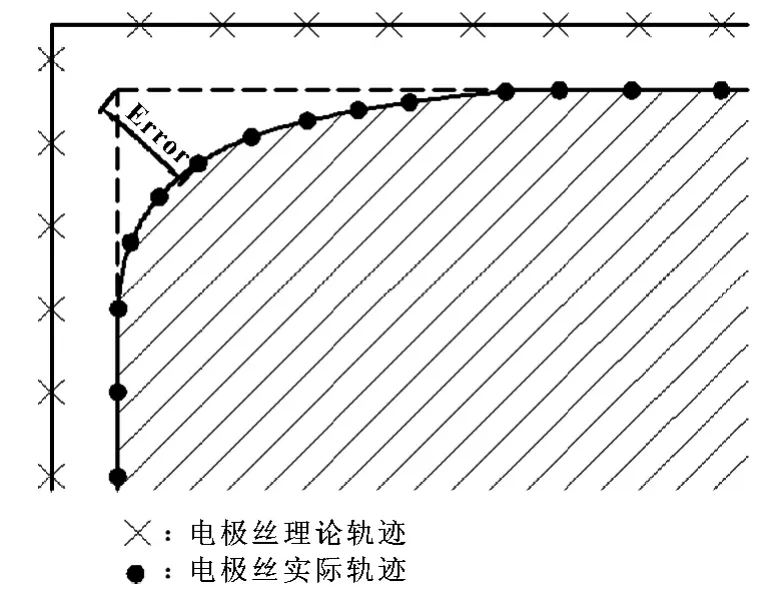
图3 拐角误差示意图

3 电极丝恒张力自适应控制系统

3.1 自适应控制系统

所谓自适应控制系统，一般指具有一定的适应环境的能力，当处于一种初始不稳定的、自身不稳定或者工作环境变化时，能够在线识别种种变化，通过一定的控制算法进行自动校正，已达到预期的控制效果的闭环控制系统。在功能上分为三部分:

(1)在线识别:通过传感器，实时地测量系统中的信号或者参数，并加以处理，识别出系统当前处于的状态;

(2)决策部分:根据系统识别出的当前状态，将其与系统设置的特征值或者参数进行比较，运用控制算法，指导系统下一步的运行;

(3)在线修改:根据决策部分所计算出来的控制参数值，传递信号给执行机构，使得控制系统的状态与设置状态无限接近。

文中研究开发的恒张力控制系统的控制流程图如图4所示。

图4 自适应控制系统控制流程图

自适应控制算法采用直接自适应控制系统，其控制算法如下:

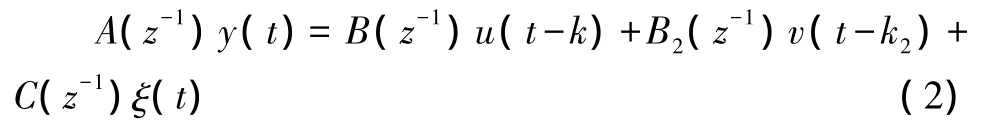
式中:y，v，u分别为系统的输出、输入和可测干扰信号;ξ(t)表示零均值的白噪声序列;k和k2是与u、v相关的传输延时;A，B，B2和C是z－1的多项式，其中C的零点在单位圆内。

引入性能指标:

式中:w表示已知的参考输入信号;P，Q，R，S是z－1的加权多项式。

3.2 恒张力控制系统

文中提出一种全新往复走丝的走丝方式，电极丝传输路线如图5所示。

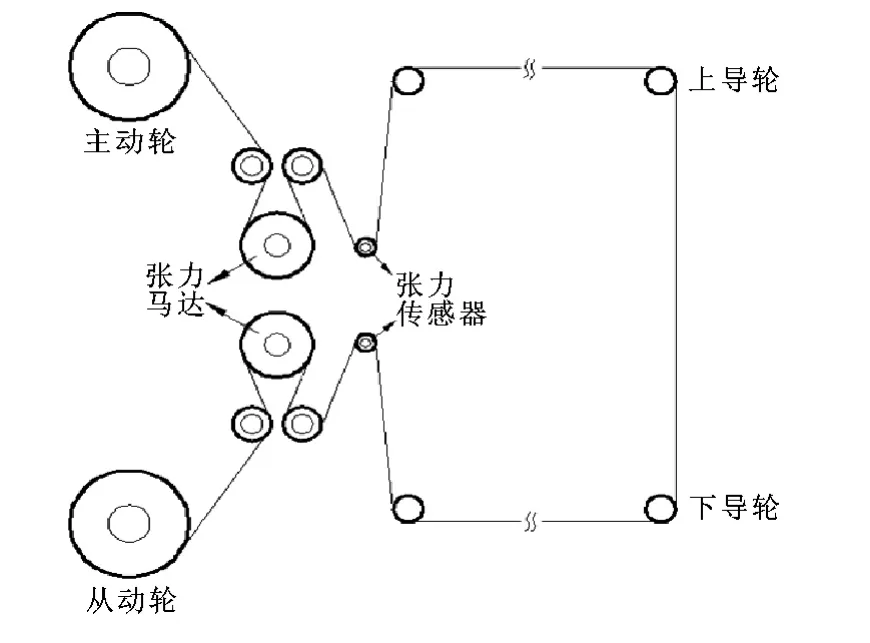
图5 恒张力控制系统电极丝走丝方式

将传统的一个丝筒贮丝循环走丝方式改为主动轮和从动轮贮丝方式，丝筒贮丝一次能够缠绕300～400 m的电极丝，主从动轮贮丝一次能够缠绕3 000～4 000 m，该走丝方式同一时间内的换向次数为原来的1/10，大大减少不必要的停顿时间，且不存在压丝的问题。主动轮为电极丝传输提供源动力，使得电极丝以一定的速度在上下导轮间传输;张力传感器为自适应控制系统的在线识别机构，能够实时测量电极丝的张紧力，并将信号传送给控制系统;张力马达为自适应控制系统的执行机构，根据控制器给出的控制信号，实时调整电极丝的张紧力。

图6为电极丝张紧力测量数据图，由图可知，当控制系统给出10 N张力值的控制信号，该系统张力值的波动在±0.4 N以内，传统走丝系统的张力值波动在±1 N以内;本系统换向瞬间电极丝张紧力波动为1 N，传统走丝系统张紧力波动为4 N，由此可见文中研究开发的恒张力闭环自适应控制系统对张紧力的控制效果显著。此外本控制系统的响应时间为5 ms，张力调节时间为1 s。

图6 张紧力测量数据图

4 控制系统实验数据验证

将文中研究开发的控制系统应用到工程实践中，与原系统进行对比，得到的性能参数如表1。

表1 文中系统与原系统性能参数对比

加工速度的提高主要是由于走丝系统的换向时间减少了90%，且电极丝的张紧力比较稳定，放电状态中正常放电的比例增加，使得材料去除率加快;表面粗糙度和形位公差的降低主要是张紧力比较稳定，电极丝的挠曲变形和振动幅度大幅降低，导轮之间的电极丝更加趋近于一条直线;断丝时间的延长主要是因为电极丝的运动特性控制得比较稳定，使得电极丝磨损降低，且放电通道内的冷却效果增加。上述性能参数对比表明，本次开发的电极丝恒张力自适应控制系统在很大程度上提高了电火花线切割机床的加工性能，对中速循环走丝线切割的发展有很大的推进作用。

5 结论

在分析电极丝的受力情况、电极丝张紧力波动原因及其对加工过程中产生的负面影响基础上，将丝筒贮丝改为主从动轮贮丝，提出一种新的走丝方式，使得走丝换向暂停时间降低为原系统的10%;增加张紧力传感器，采用自适应控制算法，研发一套闭环往复走丝电极丝恒张力控制系统，此外，该控制系统的响应时间为5 ms，张力调节时间为1 s。大量实际加工试验数据表明，该系统对电极丝的张紧力幅值波动控制在±0.4 N，并且在线切割机床的性能上 (加工速度、表明粗糙度、形位公差和断丝时间)有很大程度上的改善，对中速循环走丝线切割领域的发展有很大的指导意义。

［1］任福君，姜永成.空间曲面电火花线切割CAD/CAM系统［J］.机械工程学报，2007，43(5):214－218.

［2］丁红珍，朱敏.提高电火花线切割机床加工精度的方法［J］.机床与液压，2010，38(16):99－100.

［3］楼乐明，李明辉，彭颖红.快走丝电火花线切割加工工艺参数的优化选取［J］.上海交通大学学报，2000，34(10):1442－1443.

［4］杨蕾，蔡安江.电火花线切割加工参数对加工速度和表面粗糙度影响的研究［J］.机床与液压，2011，39(15):45－47.

［5］狄士春，黄瑞宁，于滨，等.慢走丝电火花线切割脉冲电源的研究现状及发展趋势［J］.航空精密制造技术，2004，40(6):12－16.

［6］尚婕，姜文刚，李建华，等.非对称加工电火花线切割可编程高频电源设计［J］.机床与液压，2011，39(22):24－26.

［7］TOMURA S，KUNIEDA M.Analysis of Electromagnetic Force in Wire-EDM［J］.Precis.Eng，2009，33(3):255－262.

［8］HAN F，ZHANG J，SOICHIRO I.Corner Error Simulation of Rough Cutting in Wire EDM［J］.Precision engineering，2007，31(4):331－336.

［9］BELTRANFI Ivano，BERTHOLDS Axel，DAUW Dkk.A Simplified Post Process for Wire Cut EDM［J］.Journal of Materials Processing Technology，1996，58(4):385－389.

［10］陈志，李贺，张臻，等.往复走丝线切割导轮处电极丝的挠曲变形分析［J］.机械设计与制造，2014，9(9):99－101.

［11］冯冉，蔡长韬.线切割机床电极丝振动及其有限元分析［J］.机床与液压，2010，38(23):127－130.