关于数字9的另外神奇特征

王仲才

（南昌理工学院,江西 南昌 330044）

关于数字9的另外神奇特征

王仲才

（南昌理工学院,江西 南昌 330044）

本文证明了：同一位正整数之和与其中9字打头与结尾的数之和都是9的整数倍。

正整数；9；打头；结尾；之和；之积

［引理1］［1］9的整数倍乘以任何有限位数的数之积的各位之和都是9的整数倍。

［引理2］［2］设m≥1为正整数，则m位正整数的总个数是

［定理1］ 同一位数的正整数之和都是9的整数倍

证明：设m≥1为正整数，则m位正整数是公差为1的等差数列，且首项为

由［引理2］得知尾项为

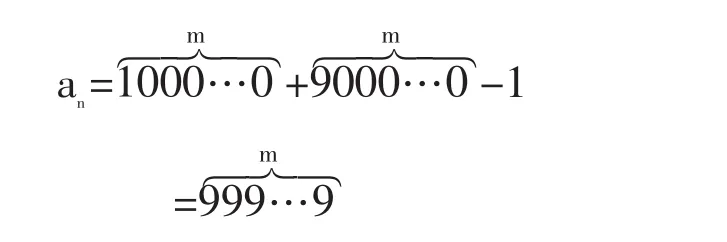
那么，总和为

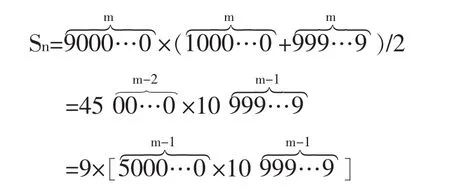
这显然是9的整数倍。

证毕。

［定理2］ 同一位正整数之和乘以任何有限位数的数之积的各位数之和都是9的整数倍。证明 由［定理1］与［引理1］即得结论。证毕。

［定理3］ 接连的9个正整数、偶数、奇数之和都是9的整数倍。

证明：设n≥1为正整数，以n开头的接连的9个正整数是公差为1的等差数列，且a1=n,与

以2n开头的9个偶数是公差为2的等差数列，且

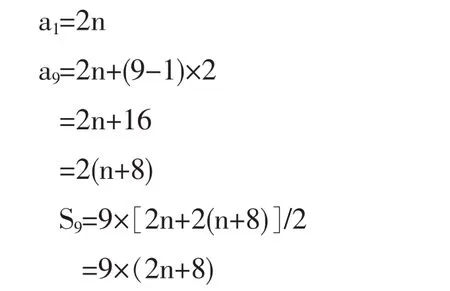
以2n-1开头的9个奇数是公差为2的等差数列，且

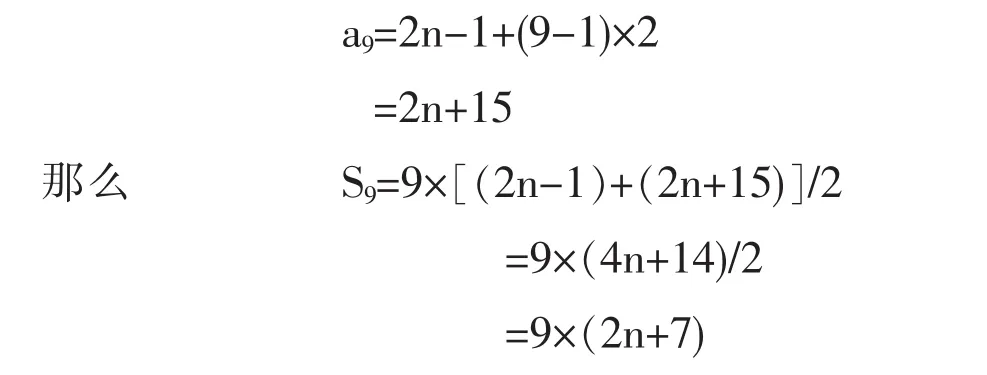
它们显然是9的整数倍。

证毕。

［定理4］ 接连的9个正整数、偶数，奇数之各之和乘以任何有限位数的数之积的各位数之和都是9的整数倍。

证明：由［定理3］和［引理1］即得结论。

［定理5］ 设m≥2为正整数，则m位正整数中，9字打头的数之和是9的整数倍。

证明 m位正整数中，9字打头的数是公差为1的等差数列，且首项为

它显然是9的整数倍。

证毕。

［定理5］ 设m≥2为正整数，则m位正整数中，9字打头的数之和乘以任何有限位数的数之积的各位数之和都是9的整数倍。

证明 由［定理4］与［引理1］即得结论。

证毕。

［定理6］ 设m≥2为正整数，则m位正整数中，9字结尾的数之和是9的整数倍。

证明：9字结尾的数是公差为 10的等差数列。

当m=2时，首项为

它显然是9的整数倍。证毕。

［定理7］ 设m≥2，为正整数，则m位正整数中，9字结尾的数之和乘以任何有限位数的数之积的各位数之和都是9的整数倍。

证明 由［定理6］和［引理1］即得结论。

［1］王仲才.关于数字9的神秘特征的数学解读的一般推广［J］.南昌理工学院学报（号外）,2009(8).

［2］王仲才.同一位数的正整数总个数其因子的整数倍的个数占总个数的比率的神奇特征 ［J］.江西广播电视大学学报，2014(4).

责任编辑：罗 义

O1

：A

1008-3537（2015）04-0095-02DOI：10.13844/j.cnki.jxddxb.2015.04.021

2015－07－27

王仲才（1939-），男，辽宁辽阳人，原南昌大学教授，硕士生导师，研究方向：几何与微分拓扑学。

http://www.cnki.net/kcms/detail/36.1211.G4.20151209.1123.042.html