移动荷载作用下加筋路堤的三维动力响应

曹周阳,杨凤云

(郑州航空工业管理学院a.土木建筑工程学院; b.继续教育学院，河南郑州　450015)



移动荷载作用下加筋路堤的三维动力响应

曹周阳a,杨凤云b

(郑州航空工业管理学院a.土木建筑工程学院; b.继续教育学院，河南郑州450015)

摘要：利用半解析方法研究移动荷载作用下加筋路堤的动力响应问题。基于Biot多孔弹性介质的波动理论，建立三维横观各向同性弹性加筋地基模型。在忽略土颗粒压缩和自重的情况下，利用Fourier变换将土体波动方程转化为常微分方程。通过数值计算研究加筋与不加筋时，速度、筋材弹性模量和加筋率等对路面竖向位移的影响。计算结果表明：在一定范围内，速度越大加筋效果越显著；速度相同时，加筋后的路面竖向位移明显小于加筋前；筋材弹性模量和加筋率在一定范围内增大时，加筋后的路面竖向位移均呈减小的趋势。

关键词：加筋路堤；动力响应；Biot方程；横观各向同性

近年来，国内高速交通快速发展，贯穿软弱土地区的高速公路路基沉陷问题不断出现，提高道路的整体稳定性是急需解决的问题。路堤加筋的主要目的是提高路堤的稳定性和承载力，减小道路的沉降，因此有必要研究加筋技术在道路工程中的应用。虽然已有学者对加筋道路的性能进行了研究，但以研究加筋路堤的静力特性为主，对移动荷载作用下加筋路堤的动力响应问题，仍停留在试验方面，理论分析很少。

目前，对动荷载作用下饱和土体的动力响应问题和二维情况下加筋路堤的响应问题进行研究[1-4]。文献[5]将移动车辆荷载简化成4个大小相等的矩形荷载，研究移动矩形荷载作用于下卧饱和土体的动力响应问题。文献[6]研究动荷载作用下加筋土的动力响应，得出加筋材料的弹性模量对土体强度有很大影响的结论。文献[7]采用有限元的方法研究了加筋层数、加筋位置、加筋间距、软基模量及路堤填筑速度等因素对加筋效果的影响。文献[8]通过分析加筋率、筋材模量、荷载移动速度等因素对路面竖向位移的影响，研究移动线荷载作用下加筋道路的动力响应问题。文献[9]将加筋路堤层简化Pasternak模型，分析速率、阻尼以及土颗粒的压缩性对加筋路堤系统的影响。文献[10]采用线弹性模型分析循环荷载作用下加筋路基的动力特性。文献[11]采用离心试验法研究地震荷载作用下土工合成材料加筋路堤的特性。文献[12]采用FLAC对土工格栅加筋路堤不同铺设位置进行数值模拟，得出格栅材料、路堤材料、填土高度、过渡段模量比和格栅铺设范围是加筋路堤的5个影响因素。文献[13]通过对路堤与软土地基之间铺设土工格栅的加筋道路和不加筋道路的动力特性的对比，得出加筋对软弱土的道路有明显影响的结论。文献[14]通过对柔性路基、带接缝板的混凝土路基以及加筋路基三者的对比研究，得出聚合物土工格栅在道路系统应用中的可行性结论。文献[15]采用有限元分析荷载形式、荷载频率、加筋位置、加筋层数、软土层厚度等因素对加筋效果的影响。上述文献大多都是基于二维情况下的加筋地基的研究，迄今为止尚很少见到针对三维弹性半空间上加筋路堤的动力响应问题的研究成果。

1动力方程及求解

1.1加筋复合土体横观各向同性参数

加筋复合道路地基一般采用分层填筑方法压实地基，填筑的材料一般等间距布置，由此，可将土体及加筋材料看作横观各向同性层的复合土体来进行研究。

加筋复合土体的加筋率[16]

式中：Vr、Ar、Hr分别为加筋单元层中筋材的体积、横截面面积和筋材的截面厚度；Vs、As、Hs分别为加筋单元层中土体的体积、横截面面积和土体的截面厚度。

由文献[8]可知：

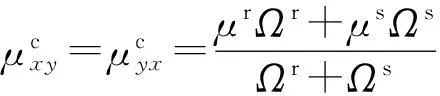
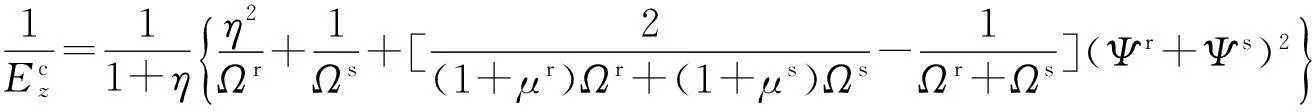
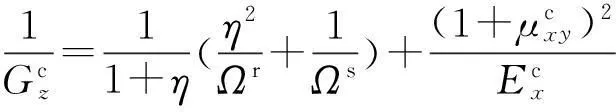
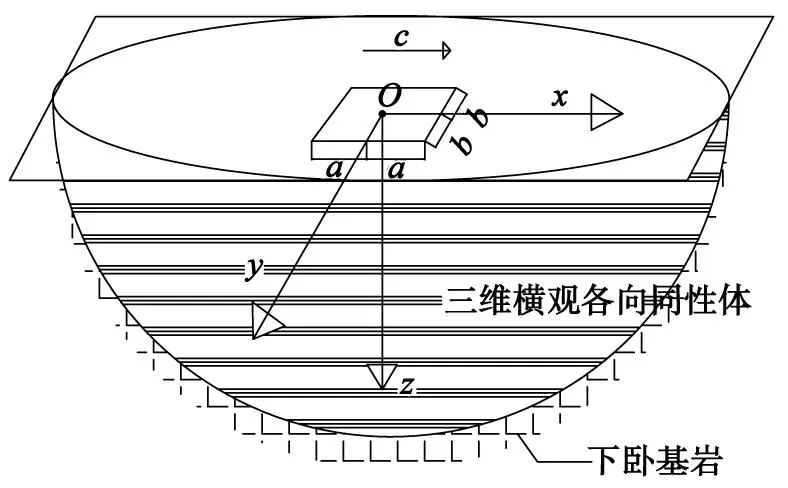
图1　三维横观各向同性弹性加筋路堤

式中：Ωr=ηEr/[1-(μr)2]，其中Er为加筋单元层中筋材的弹性模量，μr为加筋单元层中筋材的泊松比；Ωs=Es/[1-(μs)2];其中，Es为加筋单元层上体的弹性模量，μs为加筋单元层中土体的泊松比；Ψr=ημr/(1-μr);Ψs=μs/(1-μs);Ecx为加筋复合土体水平方向的弹性模量；μcxy为复合土体水平方向应力在水平方向的泊松比；μcxz为复合土体水平方向应力在竖直方向的泊松比；Ecz为复合土体竖直方向的弹性模量;Gcz为复合土体竖直方向的剪切模量。

1.2三维横观各向同性弹性体的动力方程及求解

建立如图1所示的三维横观各向同性弹性加筋路堤模型，假设三维横观各向同性弹性体位于下卧基岩上，忽略土体自重，上部为路面，忽略路面的厚度及路面自身的变形。

根据土介质中波的传播理论，在不考虑土颗粒压缩性和渗透系数的条件下，三维横观各向同性弹性体的控制方程为：

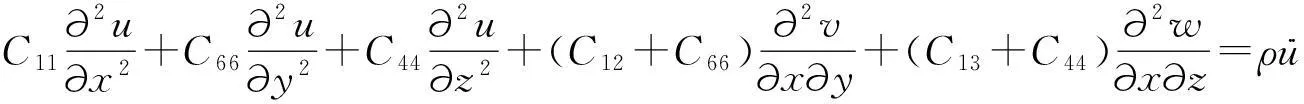
(1)

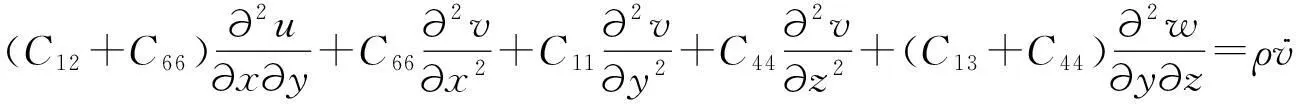
(2)

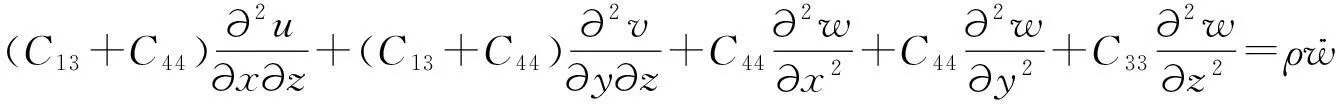
(3)

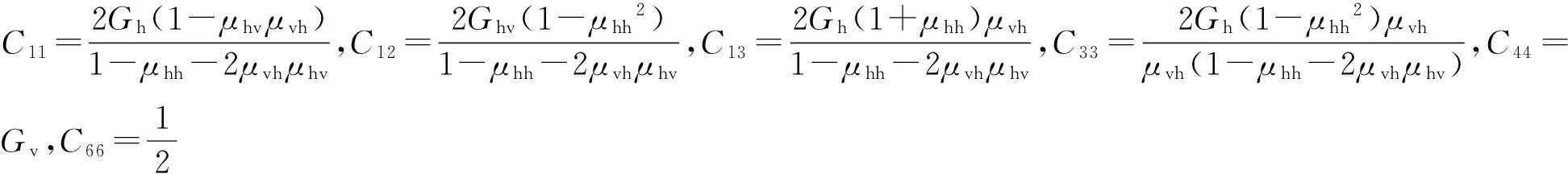
对无量纲自变量τ的Fourier变换和逆变换定义为

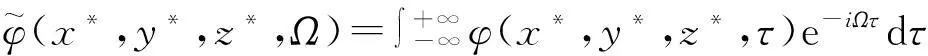
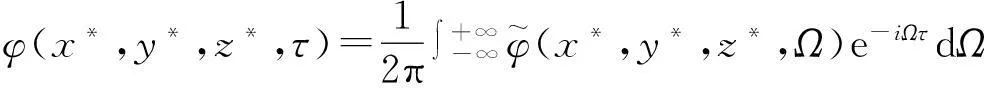
对无量纲自变量x*,y*的Fourier变换和逆变换定义为：

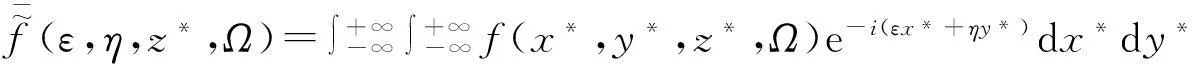
将式(1)～(3)进行Fourier变换，可得：

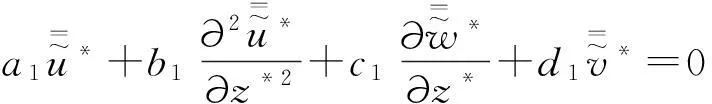
(4)

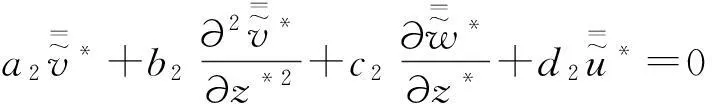
(5)

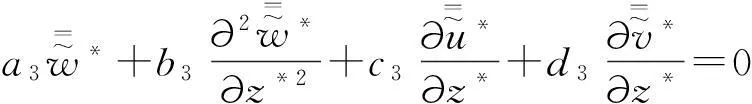
(6)

式(4)～(6)解的基本形式为：

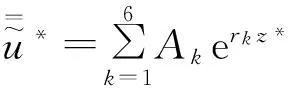
(7)

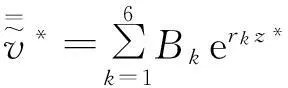
(8)

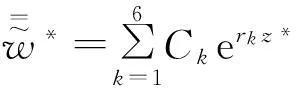
(9)

分别将式(7)～(9)代入式(4)～(6)，得：

(a1+b1r2)A+d1B+c1rC=0，

(10)

d2A+(a2+b2r2)B+c2rC=0，

(11)

c3rA+d3rB+(a3+b3r2)C=0，

(12)

要A、B、C使有非零解，则式(10)～(12)的系数行列式的值必为零，即：

(13)

设rk为式(13)的解，将rk代入式(10)～(12)得Bk、Ck的表达式：

Bk=RkAk，Ck=MkAk，

为满足半空间无限远处土体动力为零的辐射条件[17]，忽略实部为正的rk，则：

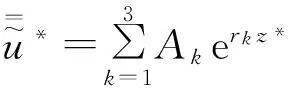
(14)

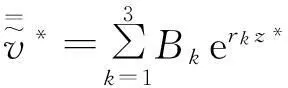
(15)

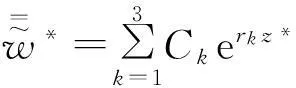
(16)

对式(14)～(16)求一次偏导，可得：

(17)

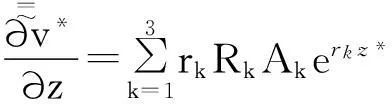
(18)

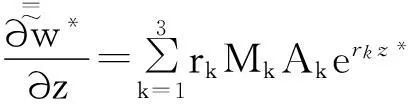
(19)

三维横观各向同性弹性介质中的应力-应变关系为：

σz=C13εx+C13εy+C33εz，

(20)

τxz=C44γzx，

(21)

τyz=C44γyz。

(22)

土动力学的几何方程为

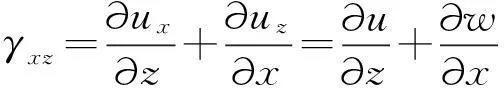
(23)

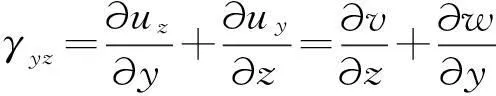
(24)

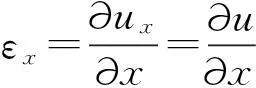
(25)

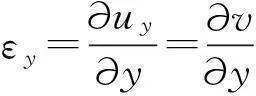
(26)

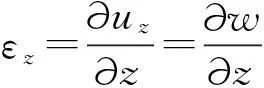
(27)

将式(23)～(27)代入式(20)～(22)可得：

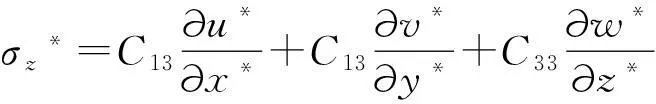
(28)

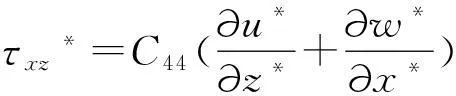
(29)

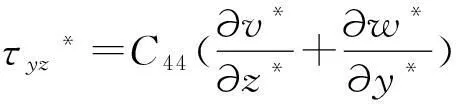
(30)

对式(28)～(30)进行三重Fourier变换(x*,y*,τ)～(ξ，η，Ω)，可得：

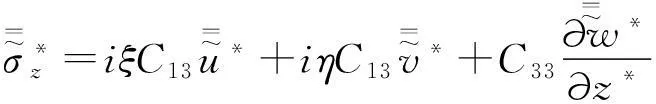
(31)

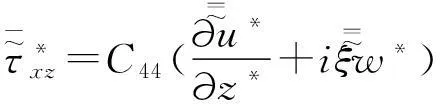
(32)

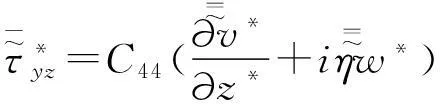
(33)

将式(17)～(19)代入式(31)～(33)中，得：

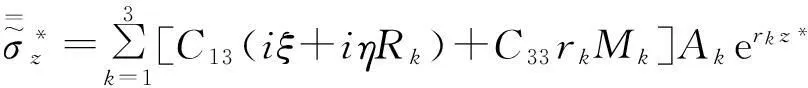
(34)

(35)

(36)

1.3模型边界条件及求解

为了求解AK1、AK2、AK3、AK4、AK5、AK6，在加筋层上表面(z=0)引入如下边界条件：

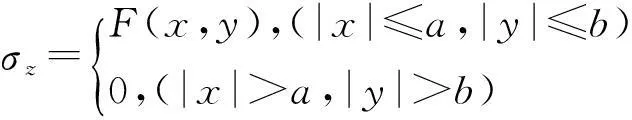
(37)

τxz=0，

(38)

τyz=0，

(39)

式中：F(x,y)为荷载集度的函数；a、b分别为荷载的长度和宽度。

对式(37)中F(x,y)应用双重Fourier变换得其变换域内的荷载表达式

式中Q为荷载幅值。

对式(37)～(39)进行Fourier变换后得：

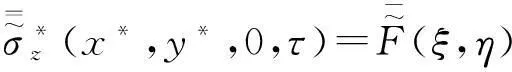
(40)

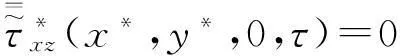
(41)

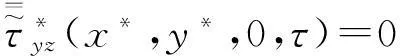
(42)

在z*=0,erkz*=1时，将式(34)～(36)代入式(40)～(42)，得：

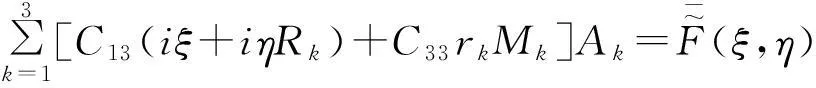
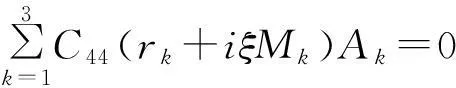
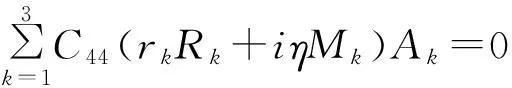
引用空间辅助坐标xt*=x*-cτ后，得三维横观各向同性弹性体的位移表达式为：

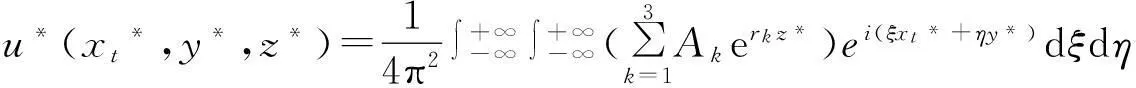
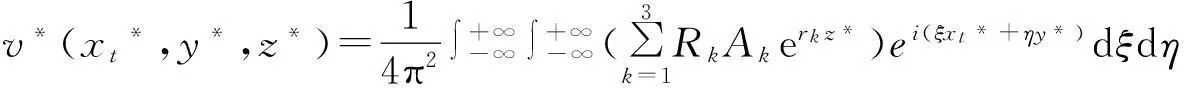
2数值计算及讨论

本文所用的计算参数见表1[5，18]。本文使用快速傅里叶变换(Fast Fourier Transform，FFT)来计算Fourier逆变换。为了使计算所得结果足够精确，按照文献[5]将-16m-1<ξ<16m-1和-16m-1<η<16m-1的区间分割为 2 048×2 048个区间进行计算，以确保足够的精度。

令Er=0，本文的计算模型退化为文献[18]中的模型，并令计算荷载强度与文献[18]相同，将本文的计算结果与文献[18]给出的土体位移进行对比，如图2所示。从图2可以看出，计算结果与文献[18]计算结果吻合较好。

表1　加筋路堤及荷载计算参数

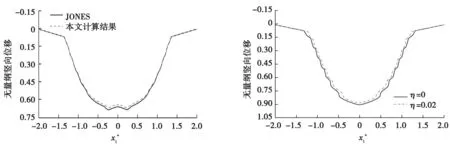
图2　本文结果与JONES结果对比　　　　　　　　　　　　图3　 速度为20 m/s时的路面竖向位移

图4　速度为150 m/s时的路面竖向位移　　　　　　　　　　　　图5　筋材模量对路面竖向位移的影响

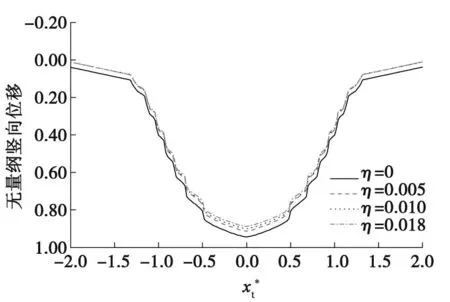
图6　加筋率对路面竖向位移的影响

3结论

本文主要研究了移动荷载作用下加筋路堤的三维动力响应，通过数值计算结果分析了加筋与不加筋时，速度对路面竖向位移的影响，以及筋材弹性模量和加筋率等对路面竖向位移的影响。计算结果表明：

1)在一定范围内，速度越大，加筋效果越显著；同一速度作用下，加筋后的路面竖向位移小于未加筋时，超过这个范围后，加筋与未加筋对路面竖向位移的影响不再显著。

2)在一定范围内，路面竖向位移随着筋材弹性模量的增大而减小，超过这一范围后，加筋模量的变化对路面竖向位移的影响不显著。

3)在一定范围内，路面竖向位移随着加筋率的增大而减小，与未加筋时相比，加筋后的路面位移明显小于未加筋时的路面竖向位移。

参考文献：

[1]BRIANCON L,SIMON B.Performance of pile-supported embankment over soft soil:full-scale experiment[J].Journal of Geotechnical and Geoenvironmental Engineering,2011,137(4):324-331.

[2]SADREKARIMI A,OLSON S M.Shear band formation observed in ring shear tests on sandy soils[J].Journal of Geotechnical and Geoenvironmental Engineering,2010,136(2):366-375.

[3] HATZIGEORGIOU G D,BESKOS D E.Dynamic inelastic structural analysis by the BEM:A review[J].Engineering Analysis with Boundary Elements,2011,35:159-169.

[4]RAJESH S,VISWANADHAM B V S.Centrifuge modeling of landfill covers[J].Journal of Geotechnical and Geoenvironmental Engineering,2011,137(4):332-342.

[5]CAI Y Q,SUN H L,XU C J.Steady state responses of poro-elastic half-space soil medium to a moving rectangular load[J].International Journal of Solids and Structures,2007,44:7183-7196.

[6]JAMSHIDI R,TOWHATA I,GHIASSIAN H,et al.Experimental evaluation of dynamic deformation characteristics of sheet pile retaining walls with fiber reinforced backfill[J].Soil Dynamics and Earthquake Engineering ,2010,30(6):438-446.

[7]朱逢斌，缪林昌，王月香.土工格栅加筋路堤的非线性数值分析[J].公路交通科技,2013,30(2):19-25.

[8]刘飞禹,赵国兴,蔡袁强，等.移动荷载下加筋道路系统的动力响应[J].浙江大学学报(工学版),2007,41(1):57-64.

[9]PRITI MAHESHWARI,KARUPPASAMY K.Nonlinear response of Infinite beams on reinforced earth beds under moving loads[C]//Geo-Frontiers 2011.Alexander,USA:American Society of Civil Engineers,2011:4683-4692.

[10]BARKSDALE R D,BROWN S F.CHAN F,Report No.315[R].Washington D C:Transportation Research Board,National Research Council,1989.

[11]WANG L P,ZHANG G,ZHANG J M.Centrifuge model tests of geotextile-reinforced soil embankments during an earthquake[J].Geotextiles and Geomembranes,2011,29(3):222-232.

[12]孙旭,冯卫江，邓永锋，等.土工格栅加筋路堤影响因素的数值模拟研究[J].交通标准化,2013(6):50-54.

[13]蔡袁强,刘飞禹,徐长节，等.交通荷载下加筋道路弹黏塑性有限元分析[J].浙江大学学报(工学版),2006,40(10):1743-1749.

[14]KELVIN C P WANG,LI Qiang.Gray clustering-based pavement performance evaluation[J].Journal of Transportation Engineering,2010,136(1):38-44.

[15]刘飞禹,蔡袁强,徐长节,等.交通荷载作用下软基加筋道路加筋效果分析[J].岩土工程学报,2007,29(11):1659-1664.

[16]CHEN T C,CHEN R H,LIN S S.A homogenized trans-versely isopropicmodel for cyclic behaviors of reinforced soil[J].Journal of the Chinese Institute of Engineers,2000,23 (1):31-40.

[17]刘飞禹，杨凤云.移动荷载作用下加筋路堤和轨道系统的三维动力响应[J].土木建筑与环境工程,2013,35(4):101-120.

[18]JONES D V,HOUEDEC D L,PEPLOW A T,et al.Ground vibration in the vicinity of a moving harmonic rectangular load on a half-space[J].European Journal of Mechanics A/Solids,1998,17(1):153-166.

(责任编辑：郎伟锋)

3-D Dynamic Response of Reinforced

Embankment Subjected to Moving Load

CAOZhouyanga，YANGFengyunb

(a.InstituteofCivilEngineeringandArchitecture;b.SchoolofContinuingEducation,

ZhengzhouInstituteofAeronauticalIndustryManagement,Zhengzhou450015,China)

Abstract:An analytical approach was used to research the 3-D dynamic response of reinforced embankment subjected to moving load. Based on Biot′s dynamic poro-elastic theory, 3-D transversely isotropic dynamic analytical model of elastic reinforced pavement were established. In the case of the hypothesis of an incompressible solid grain and neglecting the density of soil quality, the governing equations of motion were reduced to a system of ordinary differential equations by the Fourier transform. By using the numerical method, the speed of moving loads, the elastic modulus of reinforcement and the reinforced ratio were investigated. Numerical results showed that the vertical displacement of road increased with the increase of load speed in a certain range. The displacement of road with reinforced embankment was lesser than the ones without reinforced embankment. The displacement of road decreased with the increase of the elastic modulus and ratio of reinforcement.

Key words:reinforced pavement; dynamic response; Biot′s equation; transversely isotropic

文章编号：1672-0032(2015)04-0040-07

中图分类号：U416.12

文献标志码：A

DOI：10.3969/j.issn.1672-0032.2015.04.009

作者简介：曹周阳(1982—),男,河南济源人，讲师,工学博士, 主要研究方向为岩土工程与公路路基工程.

基金项目：国家自然科学 (50808119)

收稿日期：2015-09-16