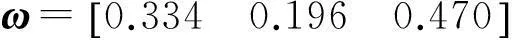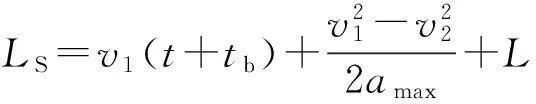基于驾驶员状态的高速公路安全车距模型

吕长民，谭德荣，于广鹏，于　洋

(山东理工大学交通与车辆工程学院，山东淄博　255049)



基于驾驶员状态的高速公路安全车距模型

吕长民，谭德荣*，于广鹏，于洋

(山东理工大学交通与车辆工程学院，山东淄博255049)

摘要：为进一步完善高速公路环境下的安全车距模型，通过道路模拟驾驶试验，确定不同车速、驾驶员不同疲劳状态下的制动反应时间域，同时根据驾驶员的眼睛状态确定驾驶员的疲劳度，基于模糊隶属函数建立驾驶员的制动反应时间与疲劳状态、车速之间的对应关系，并对高速公路环境下的安全车距模型进行实时修正。通过MATLAB仿真验证了不同驾驶员状态下车距模型的可靠性。

关键词：高速公路；隶属函数；反应时间；安全车距

截止到2014年底，我国高速公路总里程达到11.19万km，高居世界第一位[1-2]。高速公路给人们的生活带来方便的同时也带来了严重的安全隐患。据美国高速公路驾驶安全管理委员会统计，79%的汽车追尾事故是由驾驶员注意力分散造成的，如果驾驶员能够提前0.5 s发现前方车辆，追尾事故的发生率即可减少60%[3-4]。因此，高速公路环境下的安全车距准确性直接影响到汽车防追尾预警系统的有效性，对于提高人车安全有着重要意义。

文献[5]提出一种高速公路安全跟车距离的确定方法，但是没有考虑到制动反应时间(即驾驶员从发现紧急情况到右脚移动到制动踏板上的时间)的变化对安全距离的影响。文献[6]对制动反应时间进行研究，忽略了驾驶员疲劳状态的影响。本文通过高速公路模拟驾驶试验，研究不同车速、不同疲劳度下驾驶员制动反应时间的变化范围，同时根据驾驶员的眼睛状态确定驾驶员的疲劳度，建立高速公路环境下驾驶员的制动反应时间与疲劳状态、车速之间的关系，对安全车距模型实时修正，以期提高修正后安全车距模型的可靠性。

1安全车距理论模型

前后两车紧急制动情况下最小安全车距[6]

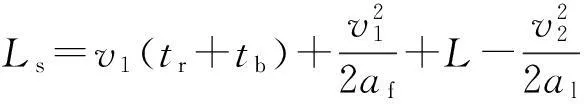
(1)

式中：L为两车完全静止时的安全车距，一般为2～5 m[7]，本文取3 m；Ls为最小安全车距；v2、v1分别为前后两车的车速；al、af为前车制动加速度与后车制动加速度；tr、tb为驾驶员制动反应时间和制动器的制动协调时间。

由式(1)的安全车距理论模型(简称模型(1))可以看出：车速与制动加速度是车辆的运动参数，tb与车辆制动性能有关，一般为200～900 ms，驾驶员制动反应时间tr是表征驾驶员特性的变量，是影响行车安全的最重要因素之一[8-9]，特别是高速公路环境下，车速较高，tr对行车安全尤为重要。

图1是驾驶员制动反应时间分别为0.6、0.8、1.0、1.2、1.4 s时高速公路环境下所需的安全车距。

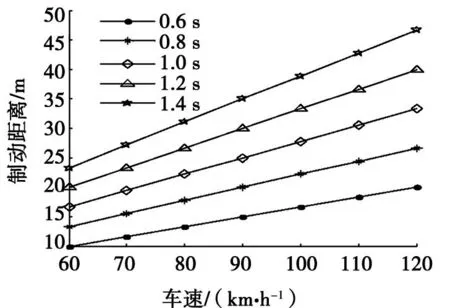
图1　不同反应时间所对应的安全车距

由图1可以看出，同一车速下，制动反应时间越长，所需的安全车距越大，车速越高，不同制动反应时间的安全车距差距就越大。模型(1)中的驾驶员制动反应时间tr采用的是固定值(1.2 s)，而实际驾驶中，制动反应时间随着驾驶员疲劳状态和车速的不同而变化，模型(1)不能反应真实驾驶状态下的安全车距。因此，本文通过分析驾驶员疲劳度和当前实际车速对制动反应时间的影响，从而对模型(1)进行修正。

2制动反应时间的确定

2.1模拟试验

通过试验模拟得出随车速及驾驶员疲劳状态变化的制动反应时间域，为三者模糊规则的建立奠定基础。试验在集成化固定驾驶模拟器上进行，通过模拟器的视景系统生成高速公路驾驶环境，进行跟车试验。通过模拟器内摄像装置记录驾驶员的操纵反应，统计驾驶员从发现紧急情况到右脚移动到制动踏板上的视频播放帧数，然后换算成驾驶员的制动反应时间。

选取身体健康、驾驶熟练的12名驾驶员为研究对象，其中男性7名，女性5名，包括5名研究生、4名中年教师、3名老教师；12名驾驶员平均年龄36岁，驾龄2～22 a，平均驾龄13 a。测试每名驾驶员不同状况(正常状况与疲劳状况)、不同车速下的应急制动反应时间。为了保证测试数据的真实性，每种状况下反复进行5次试验，剔除2次误差大的数据(表1中阴影数据为剔除数据)，对剩余3次数据求平均，共获得测试样本60例，部分数据如表1所示。

表1　不通车速、不同驾驶员状态下的制动反应时间　单位：s

1)正常状态

确保被测者睡眠充足，身体状况良好，近期内各方面均处于正常状态，上午8：00—11:00进行测试。

2)疲劳状态

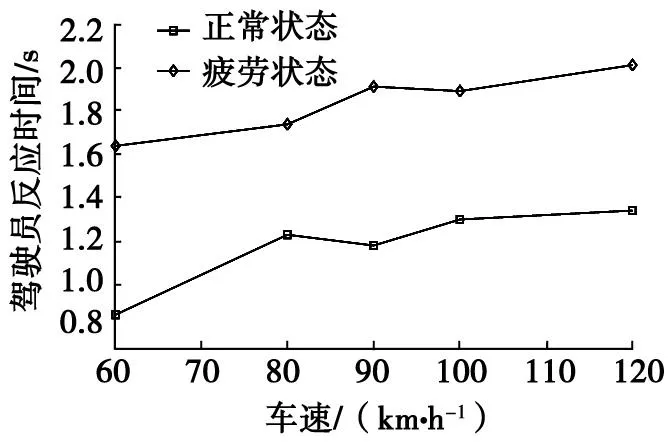
图2　两种驾驶员状态下反应时间与车速关系

被测者连续工作学习1 d后，在第2天中午进行疲劳问卷调查，符合要求的人员于下午2:00—4:00进行疲劳状态下的测试。

驾驶员在两种状态下制动反应时间与车速的关系如图2所示。由图2可以看出，相同车速时正常状态下驾驶员的制动反应时间远远小于疲劳状态下的制动反应时间。两种状态下驾驶员的制动反应时间随着车速的增加而增加，驾驶员的制动反应时间t域为[0.8，2]。

2.2驾驶员疲劳度的确定

驾驶员疲劳状态的确定可以根据驾驶员的眼部特征进行判断，人的眼部特征可以有效反映驾驶员的疲劳状态[10]。通过眼动仪选取眨眼频率、眼睛闭合率和眨眼持续时间3个眼部特征指标，通过建立的眼部特征与疲劳度之间的模糊关系获取其对应的疲劳度指标ui，并通过疲劳度评估模型综合评价驾驶员的疲劳度。

疲劳度评估模型为：

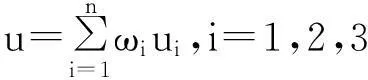
(2)

式中：u为疲劳度；u1、u2、u3分别为眨眼频率、眼睛闭合率与眨眼持续时间对应的疲劳度；ωi为ui的权重系数，其中∑ωi=1。

1)ui的确定

设驾驶员眨眼频率d域为[1,20](即每30 s的眨眼次数)，d域上包含5个模糊集合，分别代表眨眼频率低(S1)、眨眼频率偏低(M1)、眨眼频率正常(L1)、眨眼频率偏高(M2)和眨眼频率高(S2)5个状态。设疲劳度u1域为[20，100](指标值得分，分值越大表示驾驶员状态越好)，u1域上有3个模糊集合，分别代表疲劳(S)、一般疲劳(M)和正常(L)3个状态。利用典型函数法，可得驾驶员眨眼频率和疲劳度指标值的隶属函数如图3、4所示，并建立眨眼频率与疲劳度指标的模糊规则。

图3、4中，隶属度表示隶属的程度[11]，取值区间为[0，1]，其值越接近于1，表示隶属程度越高。例如图3中，S1表示模糊集“眨眼频率低”，当眨眼频率d≤2时隶属度为1，表明此时眨眼频率完全属于模糊集合“眨眼频率低”，当2

图3　眨眼频率隶属函数　　　　　　　　　　　　　　　图4　疲劳度隶属函数

建立模糊规则为IfdisS1orS2ThenuisS；IfdisM1orM2Then u isM；IfdisL1ThenuisL。

通过模糊计算，可得眨眼频率分别为4、6、8、10、12、14、16次/(30 s)时，其对应的驾驶员疲劳度u1分别为40.7、70.0、70.0、90.0、88.1、70.0、42.0。

同理，可以求出眼睛闭合率和眨眼持续时间对应的驾驶员的疲劳度u2、u3。

2)权重系数的确定

采用模糊层次分析法(AHP)确定权重系数[12]，首先通过专家打分对评价因素两两对比获取3个评价因素的权值向量。

式中ω1、ω2、ω3分别为x1、x2、x3的权重系数。

在某一眨眼频率下，例如眨眼频率为6次/(30 s)时，u1=70.0，同理某一眨眼闭合率与眨眼持续时间分别对应一个u2、u3值，代入式(2)，即可求得某一眨眼频率、眼睛闭合率与眨眼持续时间时驾驶员的疲劳度u。

2.3制动反应时间的确定

设v域为[60，120](车速小于60 km/h计为60 km/h，车速大于120 km/h计为120 km/h)，v域上有3个模糊集合，分别代表慢速(vS)、中速(vM)和高速(vL)3个状态。模拟试验得到驾驶员的制动反应时间t域为[0.8，2],t域上包括3个模糊集合，分别代表反应快(TS)、反应一般(TM)和反应慢(TL)3个状态。车速与反应时间的隶属函数曲线如图5、6所示。

图5　车速的隶属函数　　　　　　　　　　　　　　　图6　反应时间的隶属函数

基于图4～6建立车速v、疲劳度u与制动反应时间t的模糊推理规则(见表2)，如ifvisVSanduisSThentisTM[13]。根据车速与驾驶员疲劳度确定对应的驾驶员制动反应时间。

通过Matlab所建立的fuzzy模型，根据表2的模糊规则，推理出驾驶员制动反应时间、疲劳度指标和车速三者的对应关系，如图7所示，图7较图2更清晰地反应了t、u、v三者的一一对应关系。

表2　模糊推理规则

图7　驾驶员制动反应时间与疲劳度及车速的关系

3安全车距模型的修正

实时采集驾驶员眼部特征信号并综合评价驾驶员的疲劳度，根据驾驶员疲劳度、车速与制动反应时间三者间的对应关系，实时获取制动反应时间t，以该动态制动反应时间t取代模型(1)中的固定制动反应时间tr，制动器协调时间tb取0.4 s。

假设前后两车的制动加速度相等，高速公路环境下最大制动加速度为amax=6 m/s2，则安全车距模型(1)变为

(3)

将安全车距模型(1)与修正后的安全车距模型(3)进行仿真对比，不同前车车速、不同驾驶员状态下的安全车距如图8、9所示。图8、9中实线为固定反应时间的驾驶员驾车的车速与安全车距的关系(原始)，星线、点线、三角线分别为安全车距模型修正后驾驶员正常状态、疲劳状态与一般疲劳状态下驾车的车速与安全车距的关系。

由图8可以看出：当后车车速低于77km/h时，驾驶员处于正常状态下，修正模型的安全车距小于传统安全车距，原因是驾驶员的实际反应时间小于固定反应时间，因此采用传统安全车距模型得到的安全车距增加了车辆防撞预警系统的错误报警率；当车速大于77km/h时，不论驾驶员处于何种状态，修正模型的安全车距都大于传统模型安全车距，从而提高了车辆的行驶安全性。由图9可知：当两车车速都达到100km/h，且驾驶员处于正常状态时，修正模型与原始模型安全车距相差约10m，若驾驶员处于疲劳状态时，二者的安全车距相差达到18m，说明驾驶员制动反应时间的修正对于安全车距的影响很大。因此，实时判断驾驶员和车辆状态从而修正驾驶员的制动反应时间，对高速公路行车安全有重要影响[14]。

图8　前车车速60 km/h时的仿真图　　　　　　　　　　图9　前车车速100 km/h时的仿真图

4结语

1)原始安全车距模型中的驾驶员制动反应时间采用固定值，只能适用于一般情况下的安全车距。在车速较高、驾驶员状态差时安全车距偏小，行车安全性差；车速较低、驾驶员状态好时安全车距偏大，从而增加了车辆防撞预警系统的误报率。

2)通过模拟试验得到考虑车速与驾驶员疲劳度时的制动反应时间域，基于模糊隶属函数建立驾驶员的制动反应时间与疲劳状态、车速之间的对应关系，并对安全车距模型实时修正。

3)通过对比分析，验证了修正后安全车距模型的可靠性，对于提高车辆防撞预警系统安全性，降低其预警率有重要意义。

参考文献：

[1]王洪明.我国公路交通事故的现状及特征分析[J].中国安全科学学报，2009，19(10)：121-126.

[2]应世杰.高速公路汽车防撞预警系统的开发研究 [D].西安：长安大学, 2005.

[3]胡铁红.高速公路追尾及侧向碰撞预警系统模型的研究[D].西安:长安大学，2004.

[4]FRANCESCOBellaa，ROBERTARussoa.Acollisionwarningsystemforrear-endcollision:adrivingsimulatorstudy[J].ProcediaSocialandBehavioralSciences，2011，20: 676-686.

[5]杨伟，徐杰.高速公路上跟随车安全距离的一种确定方法[J].四川工业学院学报，2002，21(1)：20-22.

[6]葛如海，张伟伟.基于隶属函数的高速公路安全距离模型研究[J].中国安全科学学报，2010，20(10)：101-105.

[7]边明远.考虑驾驶员个体特性的汽车安全行驶间距模型[J].中国机械工程，2010，21(12)：1502-1506.

[8]吕集尔，朱留华，郑容森，等.驾驶员反应时间对行车安全的影响[J].交通运输系统工程与信息，2013，14(2)：80-86.

[9]于广鹏，谭德荣，田厚杰，等.基于模糊推理的驾驶员反应时间修正研究[J].广西大学学报(自然科学版), 2014, 39(6): 1234-1239.

[10]胡卓.基于人眼检测的疲劳驾驶监测技术研究[D].北京：北京交通大学, 2009.

[11]张路，王红蕾.一种适用于疲劳驾驶员的行车防追尾报警模型[J].电气技术，2014(11)：21-24.

[12]张广祥.基于驾驶行为的汽车主动防撞预警系统的安全车距研究[D].长春:吉林大学，2011.

[13]商强，谭德荣，高松，等.基于驾驶倾向性辨识的避撞-报警算法[J].科学技术与工程，2014，14(13)：282-285.

[14]KHANW,KLETTER.Stereoaccuracyforcollisionavoidanceforvaryingcollisiontrajectories[C]//IntelligentVehiclesSymposium(IV),2013IEEE.GoldCoastCity,Australia：IEEE， 2013: 1259-1264.

(责任编辑：杨秀红)

Safe Interval Model on Expressway Based on Driver State

LYUChangmin，TANDerong*，YUGuangpeng，YUYang

(SchoolofTransportationandVehicleEngineering，ShandongUniversityofTechnology，Zibo255049，China)

Abstract:In order to improve the accuracy of safe interval model on expressways, driver′s reaction time in different driving speeds and fatigue status is researched through experiments on vehicle driving simulator. And driver′s fatigue status is determined based on driver′s eye characteristics. Then the relationship of the driver′s reaction time, fatigue status and driving speed can be determined by the theory of membership function and correct safe interval model in real time. Simulations have been carried out in different driving conditions to demonstrate the reliability of vehicle safe interval.

Key words:expressway；membership function；reaction time；safe interval

文章编号：1672-0032(2015)04-0029-05

中图分类号：U491

文献标志码：A

DOI：10.3969/j.issn.1672-0032.2015.04.007

作者简介：吕长民(1989—)，男，山东泰安人，硕士研究生，主要研究方向为道路交通安全；*谭德荣(1963—)，男，山东淄博人，教授，工学博士，硕士生导师，主要研究方向为智能交通和载运工具.

基金项目：山东省自然科学基金资助项目(ZR2011EEM034、ZR2014EL036)

收稿日期：2015-09-15