高中数学中导数几何意义的妙用

苏怀堂 韩静波

（北京市第二中学亦庄学校）

在高中数学中，导数的几何意义是从“形”的角度对导数本质的定性解释，它在解决某些函数问题时能起到重要作用.本文将从以下两个角度探究导数几何意义的应用.

一、导数几何意义的应用

导数f′（x0）从代数上表示函数f（x）在x=x0处的瞬时变化率，其几何意义是曲线y=f（x）在点（x0，f（x0））处切线的斜率.因此，我们可以利用导数求切线的斜率，也可将导数转化为切线的斜率.

【例1】（2014 北京大兴一模文）给出下列函数：①f（x）=；②f（x）=x2；③f（x）=2x；④f（x）=log2x.则满足关系式f ′（2）＞f（3）-（f2）＞f′（3）的函数的序号是.

【解析】f′（2），f′（3）可分别看作函数y=f（x）在点（2，f（2）），（3，f（3））处切线的斜率，f（3）-f（2）=可看作连接（2，f（2）），（3，f（3））两点直线的斜率.

易知，①④函数图象具有共同特点：图象在（0，+∞）上都是递增且向上凸的，如图1 所示；②③函数图象具有共同特点：图象在（0，+∞）上都是递增且向下凸的，如图2 所示（其中l1表示函数在点（2，f（2））处的切线，l2表示连接（2，f（2）），（3，f（3））两点的直线，l3表示函数在点（3，f（3））处的切线）：

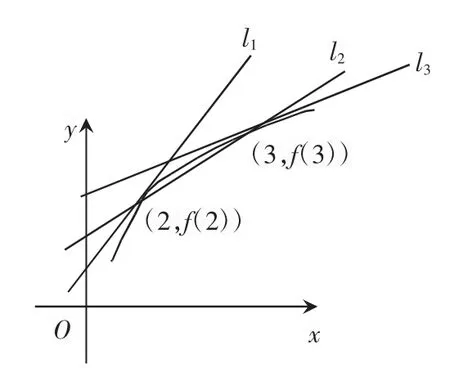
图1

图2

直线的斜率k 和倾斜角θ 的函数关系为k=tanθ（0≤θ＜π 且θ≠），其在（0上单调递增.在图1 中，l1，l2，l3三条直线倾斜角θ1，θ2，θ3均为锐角，且θ1＞θ2＞θ3，所以kl1＞kl2＞kl3，即f ′（2）＞f（3）-f（2）＞f′（3）；在图2 中，l1，l2，l3三条直线倾斜角θ1，θ2，θ3均为锐角，且θ1＜θ2＜θ3，所以kl1＜kl2＜kl3，即f′（2）＜f（3）-f（2）＜f′（3）.

所以答案为②③.

【评注】由本题可以看出，导数的本质可从数和形两个角度理解，数的角度理解为瞬时变化率，形的角度理解为切线的斜率。在数学教学中，既要帮助学生从两个角度准确理解导数的本质，又要引导学生将数和形结合起来，能灵活地进行转化。

二、导数几何意义在运动变化问题中的应用

导数f′（x0）的几何意义是曲线y=f（x）在点（x0，f（x0））处切线的斜率.它可以理解为一个运动变化过程中的一个极限，即当点P（x，f（x））沿着曲线f（x）趋向于点P0（x0，f（x0））时，割线PP0趋近于确定的位置，即y=f（x）在点（x0，f（x0））处切线，而割线的斜率趋近于y=f（x）在点（x0，f（x0））处切线的斜率f ′（x0）.因此导数的几何意义可以帮助我们解决某些图形中的运动变化问题.

【例2】（2014 年高考北京卷理数）已知函数f（x）=xcosx-sinx，x∈

（1）求证：f（x）≤0；

【说明】对于本题只解析第（2）问，并且方法更适合解决填空题.

由图可知，当P（x，sinx）从O 移动到P0时，kPO=逐渐减小，一方面，易知kP0O=，所以kPO=＞kP0O=；另一方面，当P逐渐接近O，即x→0 时，割线PO 逐渐接近于y=sinx 在O（0，0）处的切线，由导数的几何意义可知，kPO=逐渐增大到y=sinx 在O（0，0）处切线的斜率（sinx）′x=0=cos0=1，所以kPO=＜1.

【评注】由此题可知，在高中数学教学中，不但要引导学生从数和形两个角度理解导数的概念，还要帮助学生经历概念的形成过程，即从平均变化率到瞬时变化率的极限过程，也是从割线到切线的极限过程，这都是运动变化的过程。

综上所述，导数作为高中数学中的一个重要概念，教师要帮助学生从数和形两个角度理解其本质，并要重视在数和形两个方面概念的形成过程。