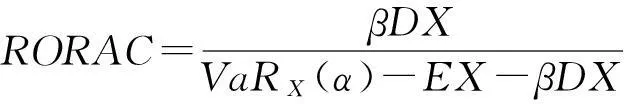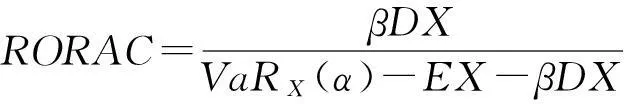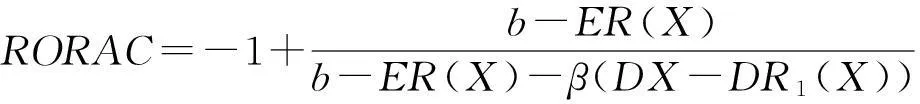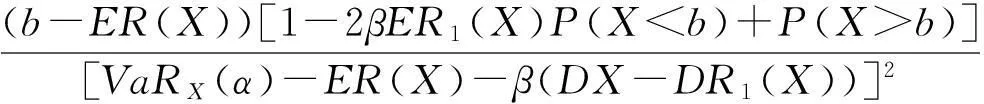风险调整资本收益率下的最优再保险策略

曹玉松

(许昌学院 信息工程学院，河南 许昌 461000)

风险调整资本收益率下的最优再保险策略

曹玉松

(许昌学院 信息工程学院，河南 许昌 461000)

摘要：在均值-方差保费计算原理下给出了最优比例再保险和停止损失再保险策略，从保险人的角度，给出了基于风险调整资本收益率最大的自留风险比率和额度， 使得保险人的风险调整资本收益率最大.

关键词：期望-方差计算原理；风险调整资本率；比例再保险；停止损失再保险

再保险指保险公司分散风险的重要途径，保险公司通过购买再保险可以有效的进行风险规避，一般地，保险人通过支付一定的保费购买再保险人的再保险，相应的将一部分风险进行转移，当索赔一旦发生，再保险人根据再保险合同的预定，承担相应的风险.

再保险过程中面临着两个重要问题，一是再保险合同衡量标准，Pesonen.M[1]讨论了原保险人的方差风险的最小，本文讨论了风险调整收益率最大下的最优再保险，20世纪70年代，美国信孚银行提出利用风险调整收益率衡量银行投资风险，此后风险调整资本收益率被广泛应用在绩效评估和风险测算中，其计算公式为

第二个问题是保费原则，即如何计算再保险的保费.Kaluszka[2]研究了在π(R)=(1+β)ER(Y)保费计算原理下的方差风险最小的停止损失再保险.Young[3,4]基于Wangs保费计算原理下，讨论了使得期末效用最大的最优比例再保险，更一般地情况参见文献[5-7].

本文的保费计算原理采取期望值保费计算原理，即

P(R)=ER(Y)+βDR(Y).

(1)

1模型

设Y原保险人在最初签订合同的整个索赔，Y为随机变量，非负；R为再保险人承担的风险，即整个索赔分为

Y=R(Y)+R1(Y)，

R(Y)为保险人的自留风险，R1(Y)为保险人的分出风险.

则保险人从保单持有人针对风险X收取的保费为EX+βDX，针对转移风险R1(X)，再保险保费为

ER1(X)+βDR1(X).

通过再保险后，保险人的剩余保费收入为

PR1=EX+βDX-ER1(X)-βDR1(X)=ER(X)+β(DX-DR1(X)).

签订再保险合同后，保险人的期末期望利润为

期望利润=PR1-ER(X)=β(DX-DR1(X)).

为了获得期望收益，保险人需要额外补入资本以提高偿付能力，根据巴塞尔II协议，我们采用给定置信水平下的风险价值来计算保险公司的偿付能力.则对自留风险R(X)，置信水平α，偿付能力要求资本为

VaRR(X)(α)=inf{y:P(R(X)>y)<1-α).

从概率论的角度而言，VaRR(X)(α)为自留风险的α分位点.因此保险人的风险调整资本为偿付能力要求资本减去剩余保费部分，即：

风险调整资本=VaRR(X)(α)-PR=VaRR(X)(α)-ER(X)-β(DX-DR1(X)) .

风险调整资本收益率定义为

(2)

本文的目的就是找到最优的比例再保险和停止损失再保险使得(2)式最大.

对于VaRR(X)(α)，我们给出如下引理

引理1如果R(X)是一个连续的单调非减函数，则

VaRR(X)(α)=R(VaRX(α)).

2最优再保险策略

目前，最常用的两种再保险策略是比例再保险和停止损失再保险，本文我们对这两种常见的再保险策略分别来讨论如何选取自留风险的比例和自留风险的额度，使得保险人的风险调资本收益率最大.

2.1最优比例再保险

设保险人的自留风险比例为1-q，即再保险函数为

R(x)=(1-q)x.

保险人的自留风险为R1(x)=qx，相应地我们通过选择合适的自留风险比例1-q使得风险调整资本收益率最大.对于比例再保险，可得结论：

定理1

若再保险合同为传统的比例再保险，则保险人的风险资本调节收益率与自留风险比率无关，其值为

证明

2.2停止损失再保险

停止损失再保险是另外一种常用的再保险函数，若自留额度为b，则原保险人承保不超过b的损失，超过b的部分由再保险人承担.即

相应地我们通过选择合适的自留风险额b使得风险调整资本收益率最大.对于该问题，我们又如下结论.

定理2保险人采用停止损失再保险

(1)当VaRX(α)

(2)VaRX(α)>b时， 此时知RORAC是b的增函数，b越大，RORAC越大，所以在b=VaRR(X)(α)时，取得最大.

(1)当VaRX(α)

(2)VaRX(α)>b时，

此时知RORAC是b的增函数，b越大，RORAC越大，所以在b=VaRR(X)(α)时，取得最大，最大为

3结语

本文的构建了风险调整资本收益率最大下的最优比例再保险和停止损失再保险模型，主要考虑了再保险过程中比例再保险和停止损失再保险，在保费采取方差计算原理的假设下，得到了比例再保险函数的自留风险比例及停止损失再保险中的自留风险额度.根据上述论证可得如下结论，若选择比例再保险，保险人自留风险越多，风险调整资本收益率越大，保险人应该根据自己的资本尽可能多的保留风险.

参考文献：

[1]PESONEN M L. Optimal reinsurances[J]. Scandinavian Actuarial Journal, 1984, 84(1): 65-90.

[2]KALUSZKA M. Optimal reinsurance under mean-variance premium principles [J]. Insurance:Mathematics and Economics, 2001, 28(1): 61-69.

[3]YOUNG V R. Optimal insurance under Wang’s premium principle[J]. Insurance: Mathematics and Ecomonics, 1999, 25(2): 109-122.

[4]YOUNG V R. Discussion of Christofides’ conjecture regarding Wang’s premium principle [J]. ASTIN Bulletin, 1999, 29(2): 191-195.

[5]GAJEK L, ZAGRODNY D. Insurer’s optimal reinsurance strategies[J]. Insurance:Mathematics and Economics, 2000, 27(1): 105-122.

[6]BUHLMANN H. Mathematical Methods in Risk Theory [M]. New York： Springer, 1970.

[7]DAYKIN C D, PENTIKAINEN T, PESONEN M. Practical Risk Theory for Actuaries [M]. London： Chapman&Hall, 1993.

Optimal Reinsurance Strategies under Return

On Risk Adjusted Capital

CAO Yu-song

(SchoolofComputerScience&Technology,XuchangUniversity,Xuchang461000,China)

Abstract:The paper addresses to the question of how to purchase proportional reinsurance and stop-loss reinsurance in order to get the insurer’s maximum risk-adjusted capital rate. In the paper, the contract is priced according to the mean-variance principle. The paper obtains the optimal retention ration and the optimal retention level respectively.

Key words:mean-variance principle; risk-adjusted capital rate; proportional reinsurance; stop-loss reinsurance

责任编辑：赵秋宇

中图分类号：O211.6

文献标识码：A

文章编号：1671-9824(2015)02-0019-04

作者简介：曹玉松(1981—)，女，河南濮阳人，副教授，硕士，研究方向：应用概率统计.

基金项目：河南省科技厅基础与前沿研究计划资助项目(132300410323)；河南省高等学校重点科研项目(15A11041);许昌市科技局基础与前沿项目(1404016)

收稿日期：2014-03-22