合理创设数学课堂情境

郑慧峰

初中生的心理发展特点决定了其数学学习在很长一个时段内需要相对具体形象的生活经验材料，因此，创设恰当的情境可以帮助学生主动学习。

一、创设生活化情境

从生活情境人手，把需要解决的问题有意识地巧妙地寓于符合学生实际的基础知识之中，把学生引入一种与问题有关的情境之中，激发学生的探究兴趣和求知欲。

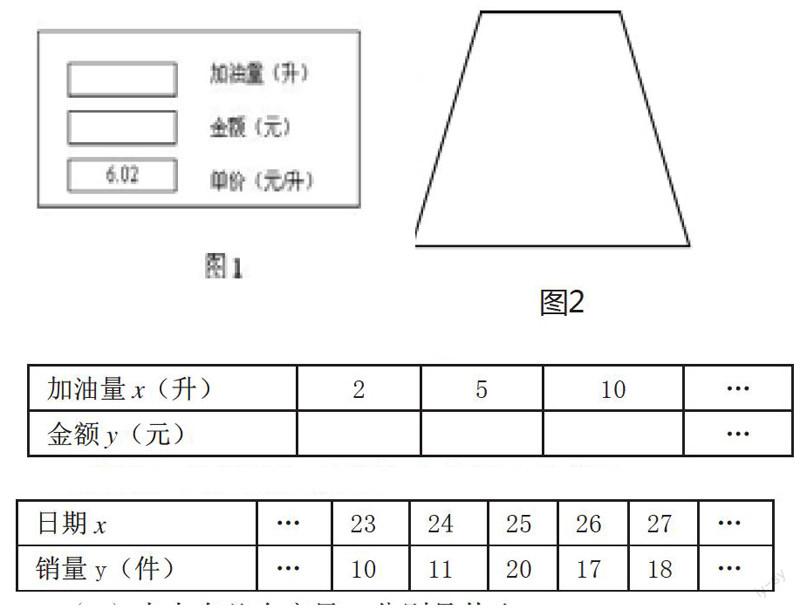
设计1：如图1

请观察加油机为汽车加油过程中能给我们哪些信息。

设计2：在此次加油过程中，加油量确定时，金额能确定吗？

设计3：观察加油机为汽车加油过程中金额y（元）和加油量（升）的变化，并填写下表：

设计4：你能用含x的代数式来表示y的值吗？

本设计从学生在身边的情境中探究新知识，引导学生把生活中体验到的量与量之间的相依关系抽象成函数中变量间的对应关系，通过这样的情境创设，让学生充分体会到数学来源于生活，又服务于生活。

二、创设活动化情境

数学活动起着引导学生经历学习过程、发展学生数学素养的重要作用，学生在数学学习活动中不仅有观察操作活动，还充满着猜想、分析、推断、迁移等探索性活动。教师要积极创设这类活动情境，让学生获得更高层次的数学活动体验，促进数学思维发展。

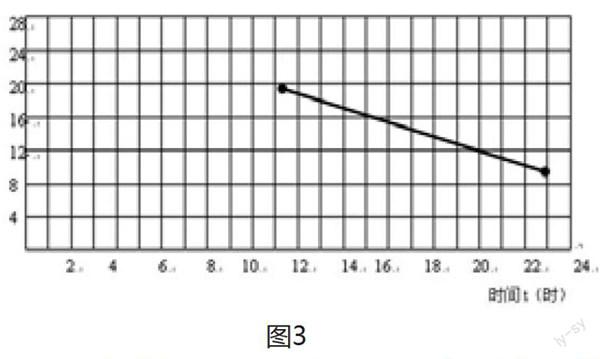
如图2：一个梯形，只剪一刀，。能否拼成一个三角形？平行四边形？矩形？若不能，至少需要剪几刀？

（1）实验器材：普通的梯形纸片若干

（2）提示问题：若要拼接，需要相等的线段，应如何剪？

本设计让学生经历“动手操作——观察——猜想——探索——论证”的全过程，学生在动手实践过程中培养了提出问题、分析问题、解决问题的能力，并积累起解决数学问题的情感体验。

三、创设问题情境

创设问题情境的核心是引导学生通过问题情境深入到数学学科的本质，超越数学概念的表面理解，真正在数学教学中实现“过程和结果并重”。

问题1：据气象台报告，25日11：00至23：00间，气温下降的速度为每小时0.7℃，假设经过时间t小时，温度下降了h℃。

（1）这个问题中，哪些是常量，哪些是变量？

（2）你能用含t的代数式来表示h吗？

（3）计算：当t分别为5，8，11时，相应的h是多少？

问题2：气温下降，国商大厦冬装旺销。下表是23日-27日某品牌冬装的销量情况。

（1）表中有几个变量？分别是什么？

（2）25日该品牌冬装的销量是多少？

问题3：如图3是25日11：00至23：00气温变化图，则图中有几个变量？如果t确定了某一个值，温度y的值是否也确定了？此时温度y的值有几个？

教师指出上面三个问题有两个共同点：其一，有两个变量；其二，当一个变量取一个值时，另一个变量有唯一确定的值，从而引出“函数”的概念。

本设计中让学生经历了分析、类比、归纳、抽象、概括等思维活动，引导了学生对函数概念进行剖析，学生真正体验到数学概念的产生过程。

合理创设数学课堂情境有助于帮助学生主动学习，促进概念的理解，引导学生把现实背景中各要素间的关系与学生已知的数学模型进行类比，促进知识迁移。