P91钢高温热损伤的非线性超声检测

孙锦中

(上海电力学院电子与信息工程学院，上海 200090)

P91钢高温热损伤的非线性超声检测

孙锦中

(上海电力学院电子与信息工程学院，上海 200090)

基于非线性超声理论，对经过不同温度热处理的P91钢试样进行了非线性超声检测试验.分析了相同激励条件下基波和二次谐波信号的频谱特性，计算出了不同温度P91钢试样的非线性系数.结果显示，随着热处理温度的升高，非线性系数逐渐增大.逐级加大激励电压，基波幅度的平方和二次谐波幅度显示了良好的线性关系，同时也表明实验测得的超声非线性系数仅与试样本身的性质有关.试验结果证明，通过对非线性系数的测量，可以对材料早期的高温损伤进行无损评价.

非线性超声;二次谐波;热损伤;P91钢

金属材料在高温环境下运行会产生高温损伤，使得材料内部晶体结构发生变化，从而导致材料晶粒增大、晶粒间产生位错等微观结构损伤.随着时间的积累，这些微观结构损伤会进一步发展，导致材料的抗拉强度、屈服强度等力学性能逐渐下降，进而有可能造成锅炉和管道爆裂等重大安全生产事故.因此，建立材料早期的高温热损伤检测和评价方法具有重要的实际价值.

目前，常规的无损伤检测方法主要有超声检测、射线检测、磁粉检测、渗透检测和涡流检测等.其中，超声检测具有灵敏度高、穿透力强、指向性好、检测速度快、成本低、设备相对简单、对人体无害等优点，因此在电站、机械制造、冶金、航空航天、航海、石油化工、铁路运输等众多工业领域中得到了广泛的应用.

近年来，非线性超声检测技术受到了越来越多的关注.大量研究表明，金属材料早期的微损伤与超声波的非线性效应关系非常密切.［1-5］与传统超声检测技术相比，非线性超声在检测由于位错等引起的材料早期弹性或塑性形变及疲劳损伤等方面有其独特的优势.传统超声检测技术测量的是时域信号，受激励探头频率的限制，其检测精度最高只能达到微米级别，而位错等材料晶体内部的变化多处于微米级至纳米级，超出了传统超声检测的能力.［6］非线性超声测量的是频域信号，通过测量基波和高次谐波的幅度可以反演出材料的非线性系数，进而借助该系数分析材料的损伤特性.

本文采用非线性超声检测方法，选用目前广泛使用于电厂锅炉主蒸汽管道及石油裂化装置中高温炉管的P91钢，对经过不同温度热处理的P91钢试样进行超声纵波无损检测，探索了不同温度下非线性系数与材料高温损伤之间的关系.

1 非线性超声检测的理论基础

一般来说，固体介质都具有非线性的特征.由于固体介质的非线性，单频正弦超声波将与固体介质间发生非线性相互作用，从而产生高频谐波.［7-8］基于这一特点，BREAZEAL等人从连续介质模型出发，建立了一维纵波非线性波动方程:

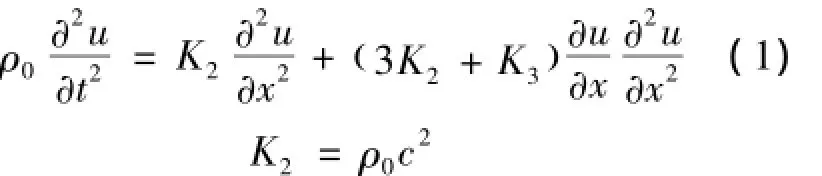
式中:ρ0——介质密度;

u——质点位移;

x——声波传播距离;

t——声波传播时间;

K2——二阶弹性常数;

K3——三阶弹性常数;

c——纵波波速.

根据式(1)定义非线性系数为:

若式(1)的初始条件为:

则可求得波动方程的近似解为:

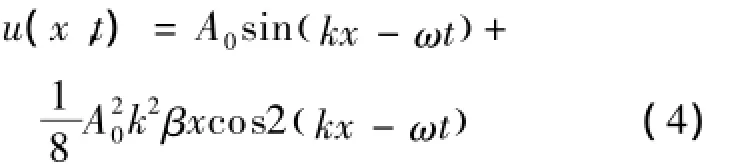
式中:ω——声波初始频率;

A0——声波初始振幅;

k——波数，k=ω/c.

由式(4)可知，基波幅度为:

二次谐波幅度为:

则联立式(5)和式(6)可得材料的非线性系数为:

若给定超声波的频率和试样长度，即k和x保持不变，则非线性系数β只与基波幅度A1和二次谐波的幅度A2相关，即:

超声波与固体介质间的非线性作用主要来自于两个方面:一是固体介质本身的晶格非谐和性;二是由固体介质晶体缺陷(如位错、微裂纹等微缺陷)引起的非线性.而研究表明，由位错等微缺陷引起的非线性要比晶格非谐和性引起的非线性大得多，在高温载荷作用下，金属材料内部的微观结构(如位错密度、位错弦长、位错组态等)都会发生变化，从而使非线性系数产生较明显的变化.因此，超声非线性系数可以作为表征材料内部疲劳损伤的重要声学特征参量，利用非线性系数可以对材料进行早期高温损伤的无损检测.［9］

2 试样的制备和实验系统

2.1 试样制备

试样材料选用P91钢，P91(9Cr1MoVNb)钢是一种改良的9Cr1Mo钢.它是在9Cr1Mo钢的基础上降低含碳量，在限制碳含量上下限、更加严格控制P和S等有害元素含量的同时，添加了一定量的N，以及微量的强碳化物形成的元素V和Nb，以达到细化晶粒、提高钢管持久强度的要求，从而形成的新型铁素体型耐热合金钢，其化学成分如表1所示.

将从同一块P91钢板上切下的6个相同尺寸的试样S0～S5作为试验用材，模拟锅炉管道的高温工作过程，对试样进行不同温度条件的热处理，热处理工艺为随炉加热至预定温度，然后保温一定时间，拿出空冷至室温.热处理后对各个试样表面进行磨削加工，使超声换能器与被测表面能够充分接触，确保对不同试样的超声测试是在相同表面状态和接触条件下进行.表2为最后得到的6个被测试样.

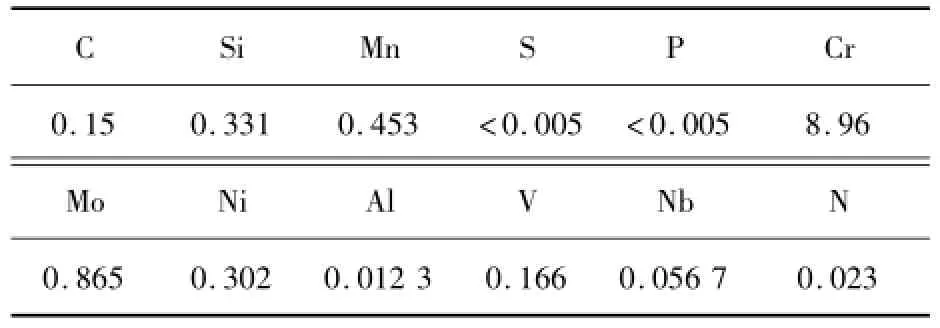
表1 P91钢的化学成分 %

热处理完毕后，采用苦味酸试剂进行腐蚀，获得了6个试样的金相组织显微照片，如图1所示.由图1可以看出，随着加热温度的升高，各个试样的内部组织发生了明显变化.原始试样的回火马氏体组织较为均匀细小，随着温度的升高，晶粒不断长大、亚晶界发生合并，组织不断增大，造成马氏体板条的粗化.其他晶内细小弥散的碳化物以及不稳定的第二相随着温度的升高很容易聚集长大，并会溶解和向其他结构碳化物转化，从而失去应有的强化作用.这些都会导致材料的组织结构发生退化，其性能也会逐步劣化，如强度降低、脆性增大等，从而导致材料的力学性能降低、使用寿命缩短.

表26 个P91钢试样的热处理规范

图16 个试样的金相显微组织

2.2 实验系统

试验所用非线性超声测试系统如图2所示.该系统由美国Ritec公司的RAM-5000 SNAP非线性超声测试系统构成，包括衰减器、放大器和滤波器组等.实验中，激励信号来源于RAM-5000 SNAP非线性超声测试系统产生的脉冲串，经衰减器、低通滤波器，激励中心频率为5 MHz的窄带铌酸锂纵波换能器产生超声波进入待测试样，接收端采用中心频率为10 MHz的宽带铌酸锂纵波换能器，接收信号经过高通滤波器和放大器返回至RAM-5000 SNAP非线性超声测试系统进行信号提取和处理.换能器和P91钢试样间采用Sonotech公司的ULTRAGELⅡ耦合剂，用一个特定的夹具来保证测试时换能器和试样之间的耦合充分稳定.同时，在测试过程中使发射换能器和接收换能器始终保持在同一轴线上，以避免能量损失，影响测试结果.

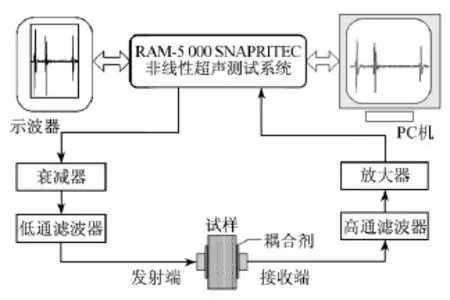
图2 非线性超声测试系统

3 实验测量

实验中为了减少仪器和随机因素产生的谐波干扰，激励信号不能在试样厚度方向上与接收信号重叠，也就是说，激励信号的脉冲宽度不能大于超声波穿过试样所需要的时间，经反复对比测试，确定激励信号的正弦脉冲串的周期数为5，脉冲宽度约为1 μs.在对不同温度损伤试样的测试过程中，保持测试系统各衰减器、放大器、滤波器等工作参数设置不变，试样厚度为20 mm，激励信号频率为5 MHz，接收到的信号包含频率为5 MHz的基波信号和频率为10 MHz的二次谐波信号.将采集到的信号传送给示波器后，利用示波器对其进行16次平均，以有效抑制测试过程中的一些随机因素的影响，提高信号的信噪比.实验所测得的基波和二次谐波的时域信号如图3所示.

对基波和二次谐波的时域信号做FFT变换，在5 MHz频率位置上可以得到基波的幅度A1，在10 MHz频率位置上得到二次谐波的幅度A2.单次测试6个试样所得到的基波幅度和二次谐波幅度的数值如图4所示.

对于基波来说，只要保持激励条件不变，基波的幅度基本就能保持不变.而对于二次谐波来说，其数值本身非常小，每次测试环境稍有不同，如超声探头与试样表面的接触情况、耦合剂的耦合程度等，都会对所测得的数值造成较大影响.本文实验中，对每个试样在同一激励信号下进行10次测量，取10次测量结果的平均值作为实验结果来进行分析和讨论.

图3 基波和二次谐波时域信号

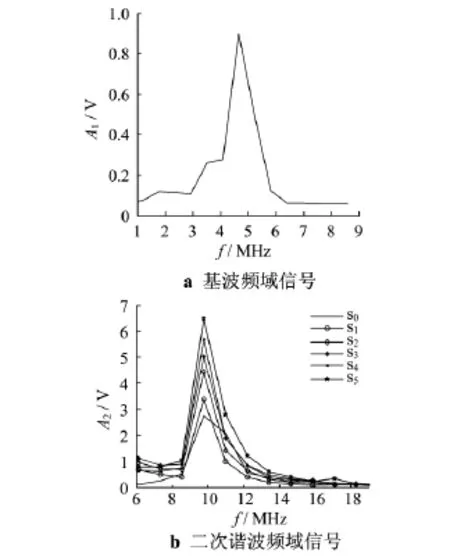
图4 基波和二次谐波的频域信号

4 实验结果分析

4.1 基波幅值与二次谐波幅值的关系

由式(7)可知，若超声发射频率和试样厚度固定不变，则二次谐波幅值和基波幅值的平方之间存在线性关系.对6个试样采用逐级增加激励信号强度的方法，测得不同的基波和二次谐波信号，再进行FFT变换，求得相应的基波幅值A1和二次谐波幅值A2，绘制出基波幅值的平方与二次谐波幅值的关系曲线图，如图5所示.

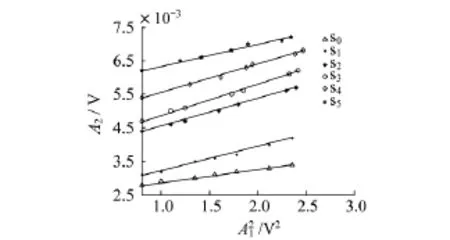
图5 基波幅度的平方与二次谐波幅度的关系

由图5可以看出，随着激励电压的增加，二次谐波幅值A2与基波幅值的平方A21存在很好的线性关系.同时也说明，实验所测得的二次谐波信号不是来源于测量系统本身的电信号，验证了实验的可靠性.

4.2 非线性系数与加热温度间的关系

对6个试样采用相同的激励信号，在试样厚度、耦合等条件均相同或相似的情况下测量10次，取平均值作为基波和二次谐波的幅度，由β=A2/A21可计算出各个试样的非线性系数.由于在试样制备过程中，只有加热温度不同，加热过程和保温时间都一样，因此可以认为本实验中非线性系数的变化只与加热温度有关.非线性系数与加热温度之间的关系如图6所示.

由图6可以看出，非线性系数随加热温度的升高而逐渐增大，加热过的试样比常温试样变化要快，后逐渐趋缓，这样的变化是因为经过不同高温损伤后P91钢内部微观结构发生了变化，位错弦长和位错密度增大，增加了材料的非线性.因此，超声非线性系数可以用于表征材料非线性的相对变化，通过对高次谐波的检测，可以对材料早期的力学性能退化和微损伤进行无损检测和评价.

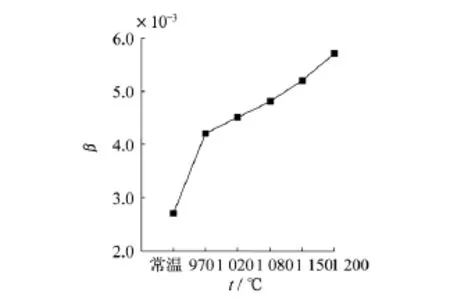
图6 非线性系数与加热温度的关系

5 结语

本文基于非线性超声波动理论，搭建了非线性超声测试系统，对P91钢的高温热损伤进行了实验研究，获得了P91钢不同温度损伤试样的基波幅度和二次谐波幅度.实验结果表明，二次谐波幅度和基波幅度的平方存在很好的线性关系.由此计算出P91钢不同温度损伤试样的非线性系数，结果显示非线性系数随加热温度的升高而逐渐增大，这说明高温损伤改变了P91钢内部的晶体结构，增加了P91钢材料的非线性，非线性系数作为一个重要参量可以用来对材料早期的高温热损伤进行无损评价.本文的研究结果对运用非线性超声纵波对材料进行高温热损伤评价具有一定的实用意义.当然，本文的实验研究是对采用非线性超声对P91钢的高温热损伤进行定性研究，接下来进一步的工作主要侧重于采用非线性超声检测手段对P91钢进行疲劳损伤超声检测、蠕变损伤超声检测，并结合电站退役的P91钢管材进行对比分析，以期建立P91钢非线性超声检测的数学模型，实现P91钢非线性超声检测在实际工程中的应用.

［1］CANTRELL J H，YOSTWT.Nonlinearultrasonic characterization of fatigue microstructures［J］.International Journal of Fatigue，2001(23):487-490.

［2］CANTRELL J H.Ultrasonic harmonic generation from fatigueinduced dislocation substructures in planar slip metals and assessment of remaining fatigue life［J］.Journal of Applied Physics，2009(9):1-6.

［3］KIM J，JACOBS L，QU J.Experimental characterization of fatigue damage in nickel-base super alloy using nonlinear ultrasonic waves［J］.The Journal of the Acoustical Society of America，2006(3):1 266-1 273.

［4］KUMAR A，TORBET C J，JONES J W，et al.Nonlinear ultrasonic for in situ damage detection during high frequency fatigue［J］.Journal of Applied Physics，2009(2):1-9.

［5］NAGY P B.Fatigue damage assessment by nonlinear ultrasonic materials characterization［J］.Ultrasonics，1998(36): 375-381.

［6］周正干，刘斯明.铝合金初期塑性变形与疲劳损伤的非线性超声无损评价方法［J］.机械工程学报，2011，47(8): 41-46.

［8］税国双，汪越胜，曲建民.材料力学性能退化的超声无损检测与评价［J］.力学进展，2005，35(1):52-68.

［9］吴斌，颜丙生，李佳锐，等.镁合金疲劳早期非线性超声在线检测实验研究［J］.声学学报，2011，36(5):527-533.

(编辑 白林雪)

Nonlinear Ultrasonic Detection of Thermal Damage of P91 Steel

SUN Jinzhong
(School of Electronics and Information Engineering，Shanghai University of Electric Power，Shanghai200090，China)

A nonlinear ultrasonic testing is implemented on P91 steel specimens thermal treated at different temperatures based on the theory of nonlinear ultrasound.The nonlinear parameter is calculated by analyzing spectrum of fundamental and second-harmonic at the same excitation conditions.The result shows that the nonlinear parameter increases with heat treatment temperature.The square of the fundamental amplitude and the second-harmonic amplitude have a good linear relationship.It is shown that the experimentally measured properties of the ultrasonic nonlinear only concerns with the nature of the sample itself.The test results show that the nonlinear parameter can be used for material nondestructive evaluation.

nonlinear ultrasonic;second-harmonic;thermal damage;P91 steel

TG115.285

A

1006-4729(2015)02-0278-05

10.3969/j.issn.1006-4729.2015.02.018

2014-09-04

孙锦中(1981-)，男，硕士，讲师，河南信阳人.主要研究方向为超声无损检测方法及信号处理.E-mail:benima2001@sina.com.