单域时滞电力系统的滑模负荷频率控制

刘永娟，米 阳，吴 晓

(上海电力学院电气工程学院，上海 200090)

单域时滞电力系统的滑模负荷频率控制

刘永娟，米 阳，吴 晓

(上海电力学院电气工程学院，上海 200090)

针对包含时滞不确定性和参数不确定及负荷扰动的单域电力系统，提出了滑模负荷频率控制策略.通过Matlab/Simulink平台，搭建仿真算例，检验所提出的控制器在时滞电力系统不同工作点运行且考虑发电机变化约束(GRC)的情况下的鲁棒性和控制性能.仿真结果显示，与不含滑模控制的时滞电力系统相比，采用滑模控制器使时滞系统的响应速度快，并且具有更好的鲁棒性.

负荷频率控制;时滞系统;滑模控制;电力系统

频率是电力系统运行最重要的参数之一.［1］频率稳定是电力系统安全稳定运行的重要因素，一个系统的频率依赖于有功功率的平衡，有功功率在某一点上的需求变化可以通过频率的变化反映到整个系统.当负荷快速变化时，发电机来不及应对而会产生频率波动，特别是当负荷变化较大时，频率偏差可能就会超过允许的范围.［2］频率波动的实质就是负荷功率和发电机输出有功功率之间的不平衡，因此需要通过频率的3次调整控制，即电力系统负荷频率控制(LFC)使得频率保持在电力工业允许的范围之内.［1-3］

随着现代电力系统的解除管制和电力市场的发展，传统的专用封闭的通信网络越来越无法满足电力系统通信发展的需要，而随着开放型的通信网络结构的引入，LFC中不可避免地存在固定和随机的通信延迟，时滞的引入会降低控制系统的控制效果甚至引起整个闭环系统不稳定，因此设计考虑时滞影响的控制器成为时滞电力系统控制的一个关键问题.实际中，在AGC控制信号获取和通信过程中必然产生AGC信号的延时问题，现仅简化考虑AGC指令通信所造成的延时对系统AGC控制效果的影响.

国内外学者对LFC问题进行了大量的研究，传统的LFC方法主要是利用现代控制论中的PI控制方法来实现的，［2-3］但控制器的参数优化严重依赖系统的分模型结构及参数.随着电力系统的发展，其结构日趋复杂，系统的结构与参数都存在不确定性，并且系统受到多样负荷扰动的影响，电力系统中包含大量的非线性和不确定环节，使得传统的PI控制调节效果变差，很难实现预期的控制目标.为此，研究人员不断地改进PI负荷频率控制策略，并且将模糊控制、神经网络、预测控制和自适应控制等先进控制理论应用到电力系统的负荷频率控制设计中.［4-8］这些方法在一定程度上解决了系统不确定性的影响，但也存在控制复杂、鲁棒性差等不足.

滑模控制作为典型的非线性控制，具有响应速度快、对系统参数不确定和外部干扰呈现不变性的优点，并且算法简单，易于工程实现.因此，现在许多电力系统负荷频率控制设计中应用了滑模控制理论.文献［9］针对阶跃负荷变化情况下的电力系统，设计了常规的滑模负荷频率控制器，仿真结果显示该控制器比PI控制器具有更好的鲁棒性.文献［10］中滑模变结构控制参数Tp变化20%时，系统的动态特性几乎不受影响，但在考虑GRC及死区非线性的影响时，系统不收敛且有时还会引起不稳定.文献［11］结合了基于ACEN的PI控制和滑模控制二者的优点，提出了一种多域互联电力系统PI滑模综合LFC的方法，采用积分滑模控制思想，使系统一开始就进入滑模状态，滑模存在于整个控制过程中.以上方法均未考虑通信时滞对电力系统稳定性的影响.

基于以上研究分析，本文针对非匹配不确定电力系统，设计了针对时滞电力系统的滑模负荷频率控制器.其优点主要包括3个方面:一是在常规的电力系统模型中加入了由于通信延迟造成的时滞环节，系统模型更贴切电力系统的实际运行状态;二是设计滑模负荷频率控制器时，对于所研究电力系统中的时滞不确定性和参数不确定项及负荷扰动没有匹配条件的要求，因此更具有一般性;三是分别对发电系统在不同工作点和发电机受限(GRC)的情况下进行分析和仿真研究，证明了所设计的滑模控制器对系统中的不确定性干扰和非线性死区具有较好的抑制效果.

1 带有时滞的电力系统负荷频率控制模型

电力系统是复杂的非线性动态系统.由于电力系统在正常点运行时负荷变化很小，因此可以用线性化模型来表示正常工作运行点附近的系统动态过程.［12］在常规LFC电力系统模型的基础上，考虑通信延迟的影响，加入了时滞环节e-sτ，［13］得到单域系统时滞模型如图1所示.

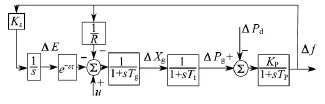
图1 单域时滞LFC系统动态模型

考虑电力系统满足如下数学模型:

式中:Δf(t)——频率偏差，Hz;

ΔPg(t)——发电机输出功率的变化量;

ΔXg(t)——调速器阀门位置的变化量;

ΔPd(t)——负荷扰动量;

Tg——调速器时间常数，s;

Tt——汽轮机时间常数，s;

Tp——电力系统模型时间常数，s;

Kp——电力系统增益;

R——调速器的调节参数;

τ——时滞常数，此处取正实数，τ＜τd，τd表示时滞裕度.

为了对频率偏差进行有效调节，增加了频率偏差Δf(t)的积分控制项为:

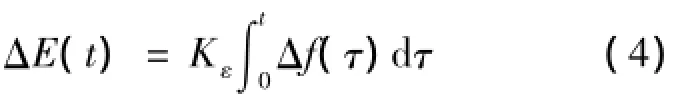
则有:

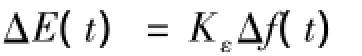
式中:ΔE(t)——积分控制增量;

Kε——积分控制增益.

由于电力系统中的负荷是不断变化的，因此电力系统的工作点也随之不断调整，使得电力系统中存在由于不同工作点变化而产生的参数不确定项.为了更准确地描述实际的电力系统，将模型(1)至模型(4)重新定义为如下不确定状态向量模型为:

式中:

ΔA，ΔAd，ΔB，ΔH均为电力系统参数的变化量.

2 滑模负荷频率控制器的设计

滑模控制器的设计原理可以参考文献［9］和文献［14］.滑模控制器的设计包括切换面设计和控制器设计两个部分.设计的控制器需要保证系统的状态轨迹可以从任意初始值到达切换面，并且保持在滑动模态附近.

为了方便滑模控制器的设计，定义如下集结不确定项:

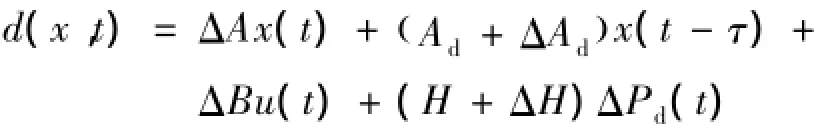
则式(5)可以表示为:

为了证明的需要，首先给出如下假设.

假设1:存在已知的正函数β(x，t)，使‖d(x，t)≤β(x，t)‖，‖＊‖表示欧几里德范数.

在实际电力系统中，负荷会在一定范围内发生波动变化，所以集结的参数不确定项是一个有界函数，假设1在实际系统中是满足的.

假设2:系统矩阵(A，B)是可控的.

2.1 切换面设计

针对式(6)设计切换面s(t)满足如下方程:

式中:C——切换增益矩阵，由极点配置［9］得到，且CB非奇异.

当系统达到滑动模态时满足s(t)=0.因此通过使.s(t)=0，即:

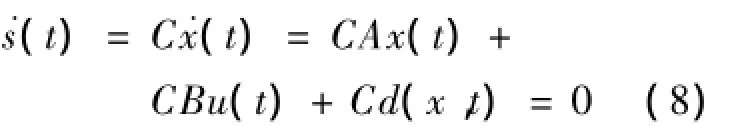
可得到等效控制:

将式(9)代入式(6)，得到系统滑动模态下的等价方程为:

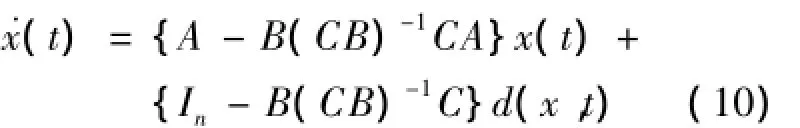
定理1如果条件‖~D(x，t)‖≤β1(x，t)成立，则存在:

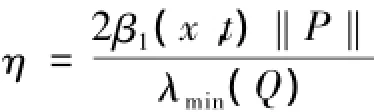
使得对于所有的t和x∈Bc(η)不确定电力系统在滑模面s(t)=0上保持稳定.

证明令:

则式(10)可表示为:

构造李雅普诺夫函数:

对v(t)求导并将式(12)代入，得:

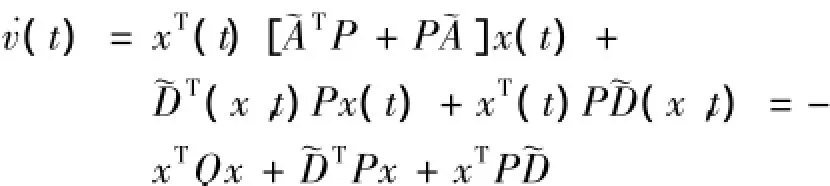
式中:P——李雅普诺夫方程~ATP+P~A=-Q的解.

对于给定的正定对称矩阵Q，可以证明式(14)可归纳为:

由于λmin(Q)＞0，所以对于所有的t，当x∈Bc(η)时，系统是稳定的.其中Bc(η)是以x=0为球心，η为半径的封闭球面B(η)的补.

2.2 控制器设计

式(6)中的不确定系统满足假设，利用如下趋近律［9］设计变结构控制器，即:

式中:n，m——正常数;

sgn——符号函数.

定理2设计滑模控制器满足如下方程:

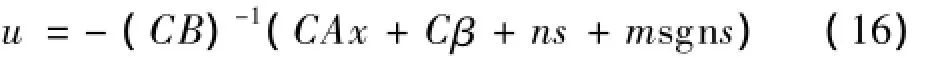
则系统满足到达条件.

证明由式(7)和式(15)可得:

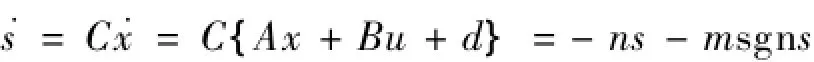
则s·.s＜0，系统满足到达条件.

综上，控制器能够使系统的运动轨迹保持在滑动模态附近.

3 数例仿真

3.1 系统参数变化对系统的影响

为了验证所设计滑模负荷频率控制器的有效性，下面进行仿真研究.本文采用与文献［12］相同的算例模型，系统参数取值见表1.

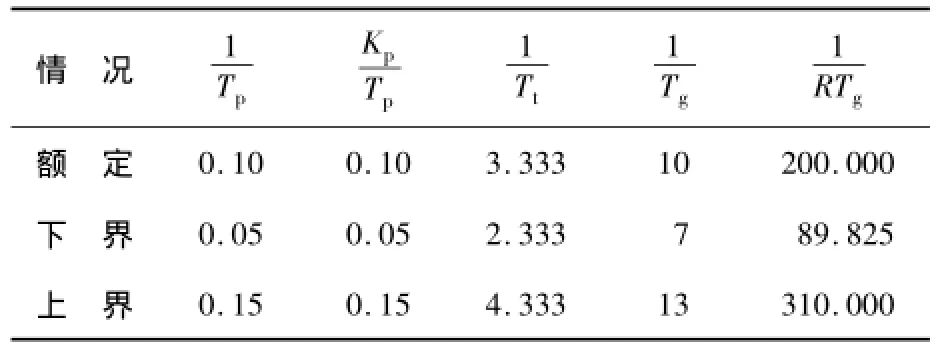
表1 电力系统的模型参数值

由于电力系统中负荷的波动性引起工作点的变化，使得电力系统存在参数不确定和负荷扰动.其中，电力负荷呈1%的阶跃变化，如图2所示.

系统参数Tt和Tg的变化范围是相对其标准值变化量的30%，其他参数取相对其标准值变化量的50%.［12］仿真参数的取值情况如表1所示.

当系统参数为额定参数时，系统频率偏差如图3所示.

当系统参数经过ΔA1，ΔB1，ΔH1，ΔAd1调整至下界时，系统频率偏差如图4所示.

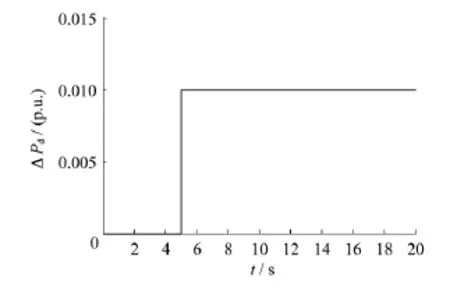
图2 负荷扰动模型

图3 额定参数时频率偏差Δf的响应

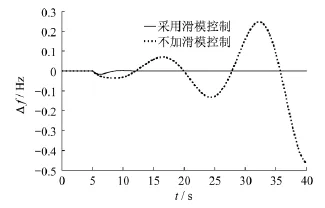
图4 下界参数时频率偏差Δf的响应

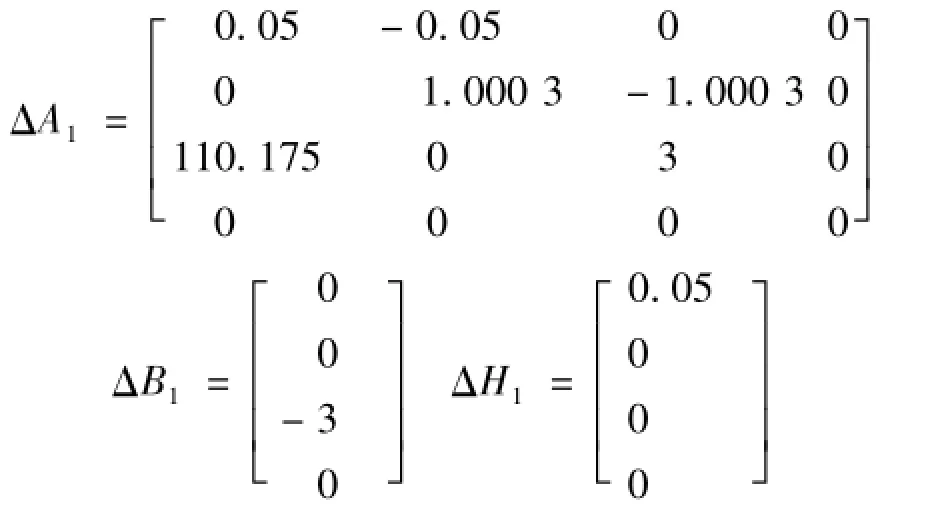
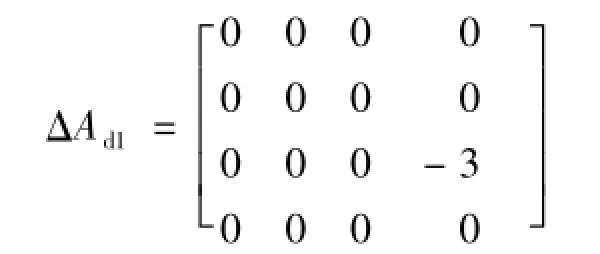
当系统参数经过ΔA2，ΔB2，ΔH2，ΔAd2调整至上界时，系统频率偏差及发电机输出功率响应如图5所示.其中:

图5 上界参数时频率偏差Δf的响应

由仿真结果可知，在1%阶跃负荷扰动下，当系统参数为额定参数时，两种控制策略都能将系统频率偏差控制在工况要求的±0.2 Hz以内.但采用滑模控制(SMC)的模型在t=10 s后频率偏差保持为零，而不加滑模控制的模型的频率偏差曲线呈衰减震荡趋势，经过一段时间后才能为零.当系统参数为下界时，采用滑模控制(SMC)的模型在t=10 s后频率偏差保持为零，响应速度快，超调量小.而不加滑模控制的模型的频率偏差曲线呈渐扩震荡趋势，系统无法达到稳定状态.当系统参数为上界时，两种控制模型都能将系统频率偏差控制在工况要求的±0.2 Hz以内.采用滑模控制(SMC)的模型在t=10 s后频率偏差保持为零，响应速度快且超调量小.不加滑模控制的模型的频率偏差曲线呈衰减震荡趋势，t=80 s时系统频率偏差才为零，且函数及控制器的切换增益均大幅降低.综合上述3种情况可以得出，相比于不加滑模控制的模型，采用滑模控制(SMC)的模型在系统存在参数不确定项和时滞不确定性时，系统仍能保持较快的响应速度，且超调量小，系统本身具有较强的稳定性.

3.2 考虑发电机变化率约束(GRC)的影响

在讨论上述3种情况时，并没有考虑发电机变化率约束(GRC)的影响.在实际的电力系统中，发电机输出功率的变化率是存在最大限值的，并且GRC对系统的动态响应具有不可忽略的影响.［15］受GRC作用的电力系统模型见图6.

图6 考虑GRC的电力系统动态模型

为了深入验证本文提出的时滞单域滑模控制(SMC)，同时考虑GRC与参数变化对系统响应的影响，分以下两种情况来讨论标称系统的响应情况.

若系统参数为标称参数，在不同GRC约束下，频率偏差曲线如图7所示.

图7 标称参数时不同GRC约束下频率偏差Δf的响应

由仿真结果可知，GRC越小，系统的超调量越大，振荡时间越长.

若保持GRC恒定为δ=0.01(p.u.)，在不同系统参数情况下系统频率偏差的响应如图8所示.

由以上仿真结果可以看出，针对不同的GRC情况，所设计的DOB-SMC控制器都能有效控制电力系统的频率偏差.

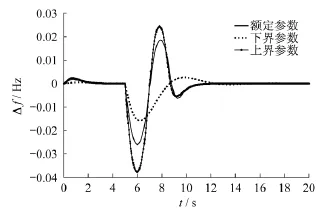
图8 相同GRC下不同系统参数的频率偏差Δf响应

4 结论

(1)本文设计了考虑电力系统通信延迟的滑模负荷频率控制器，检验其在不同工作点运行和考虑发电机变化约束(GRC)的情况下的鲁棒性和控制性能.文中所利用的系统模型加入了时滞环节，更符合实际电力系统运行状态.

(2)考虑受到负荷扰动、系统参数变化及GRC的情况下，将采用滑模负荷频率控制器和不加控制的负荷频率控制模型效果进行对比，仿真结果显示，本文所设计的控制器具有更快的响应速度和更高的精度，能更加有效地抑制频率偏差.

［1］高翔，严正，李瑞超，等.现代电网频率控制应用技术［M］.北京:中国电力出版社，2009:25-60.

［2］FOSHA C E，Elgerd O I.The megawatt-frequency control problem:a new approach via optimal control theory［J］.Power Apparatus and SystemsIEEE Transactions on，1970(4): 563-577.

［3］ANDERSON P M，FOUAD A A.Power system control and stability［M］.John Wiley＆Sons，2008:3-366.

［4］BIRCH A P，Sapeluk A T，Ozveren C S.An enhanced neural network load frequency control technique［C］//Control，1994.Control＇94.International Conference on.IET，1994:409-415.

［5］HA Q P.A fuzzy sliding mode controller for power system loadfrequencycontrol［C］//Knowledge-BasedIntelligent Electronic Systems，1998.Proceedings KES＇98.1998 Second International Conference on.IEEE，1998:149-154.

［6］罗兵，章云，黄红梅.小波神经网络与PID相结合的负荷频率控制［J］.电力自动化设备，2006，26(1):25-28.

［7］MUYEEN S M，HASANIEN H M，TAMURA J.Reduction of frequency fluctuation for wind farm connected power systems by an adaptive artificial neural network controlled energy capacitor system［J］.IET Renewable Power Generation，2012，6(4): 226-235.

［8］ANNAKKAGE U，HUGHES F M.Load frequency control using self-tuning techniques［J］.International Journal of Control，1987，46(2):423-439.

［9］高为炳.变结构控制理论基础［M］.北京:中国科学技术出版社，1990:90-149.

［10］AL-Hamouz Z M，ABDEL-Magid Y L.Variable structure load frequencycontrollersformultiareapowersystems［J］.International Journal of Electrical Power＆Energy Systems，1993，15(5):293-300.

［11］孟祥萍，薛昌飞，张化光.多区域互联电力系统的PI滑模负荷频率控制［J］.中国电机学报，2001，21(3):6-11.

［12］WANG Y，ZHOU R，WEN C.New robust adaptive loadfrequency control with system parametric uncertainties［C］∥Generation，Transmission and Distribution，IEE Proceedings.IET，1994(3):184-190.

［13］LI Jiang，YAO W，WU Q H，et al.Delay-dependent stability for load frequency control with constant and time-varying delays［J］.Power SystemsIEEE Transactions on，2012，27(2): 932-941.

［14］刘金琨.滑模变结构控制Matlab仿真［M］.北京:清华大学出版社，2005:22-108.

［15］米阳，吴晓，楚瀛，等.基于滑模控制的单域电力系统负荷频率控制［J］.控制与决策，2012，27(12):1 881-1 884.

(编辑 白林雪)

The Sliding Mode Load Frequency Control of Single Area Time Delay Power System

LIU Yongjuan，MI Yang，WU Xiao
(School of Electrical Engineering，Shanghai University of Electric Power，Shanghai200090，China)

The strategy of a single area power system load frequency sliding mode control is proposed for the single area power system with parameter uncertainties and load disturbance.Through the platform of Matlab/Simulink，its robustness and control performances of the proposed controller are examined when the power system is at different operating points and under GRC.The simulation results show that time delay system with sliding mode controller has a quicker response and better robustness than the one without sliding mode controller.

load frequency control;time delay system;sliding mode control;power system

TM715;TM921.51

A

1006-4729(2015)02-0293-06

10.3969/j.issn.1006-4729.2015.03.021

2014-09-24

刘永娟(1989-)，女，在读硕士，河北邢台人.主要研究方向为电力系统负荷频率控制.E-mail: liuyjuan89@163.com.

国家自然科学基金(61403246);上海绿色能源并网工程技术研究中心项目(13DZ2251900).