一类非自治Birkhoff系统的梯度表示

张毅

（苏州科技学院土木工程学院，江苏苏州215011）

一类非自治Birkhoff系统的梯度表示

张毅

（苏州科技学院土木工程学院，江苏苏州215011）

研究非自治Birkhoff系统的梯度表示。给出一类非自治Birkhoff系统和非自治广义Birkhoff系统成为梯度系统的条件，并举例说明结果的应用。

非自治Birkhoff系统；梯度系统；势函数；稳定性

1 梯度系统

如果存在函数V=V（x1，x2，…，xm），使系统的微分方程表示为

则该系统称为梯度系统[1]，其中V=V（x）称为势函数。

梯度系统是一个数学系统，具有重要性质[1]：对所有x，有，当且仅当x是平衡点有；在平衡点处特征根是实的。利用这些性质研究力学系统的平衡位置及其稳定性，可先将力学系统化为梯度系统。

下面，研究非自治Birkhoff系统和非自治广义Birkhoff系统的梯度表示。

2 非自治Birkhoff系统的梯度表示

Birkhoff系统的运动微分方程为[10]

小学生天性活泼、好玩，如果在练习听力的过程中，让他们进行简单、单一的练习，他们肯定会觉得很枯燥，进而产生讨厌听力的学习，甚至对英语学习失去兴趣。皮亚杰说过：“所有智力方面的工作都要依赖于兴趣。”可以说，要想真正提高学生听力技能，培养兴趣是非常重要的。所以，为了让学生进行有趣的听力练习，教师在听力教学中要开展灵活多样的听力活动。

其中B=B（t，a）为Birkhoff函数，Rμ=Rμ（t，a）为Birkhoff函数组。如果Birkhoff函数B和Birkhoff函数组Rμ都显含时间t，则称为非自治的[10]。

假设系统非奇异，则方程（2）可表为

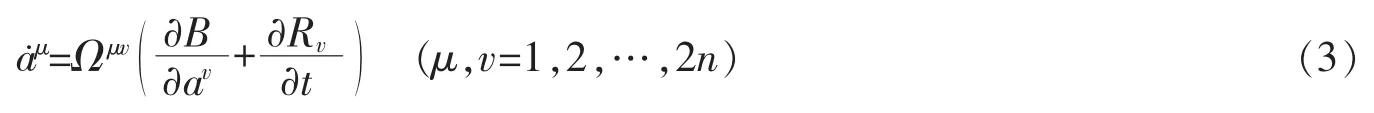
一般而言，非自治Birkhoff系统不是一个梯度系统。

如果满足条件

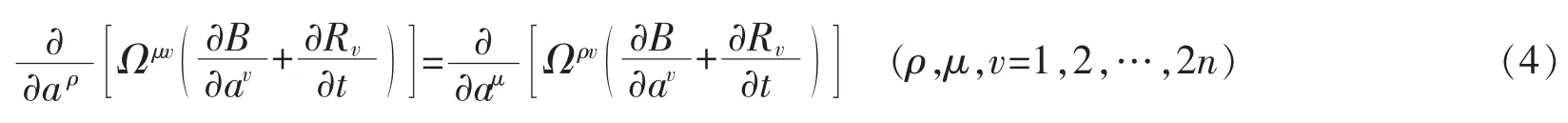
以及

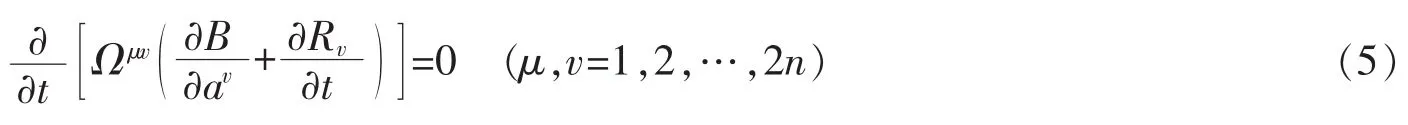
则方程（3）是一个梯度系统。此时，可找到势函数V=V（a），使得

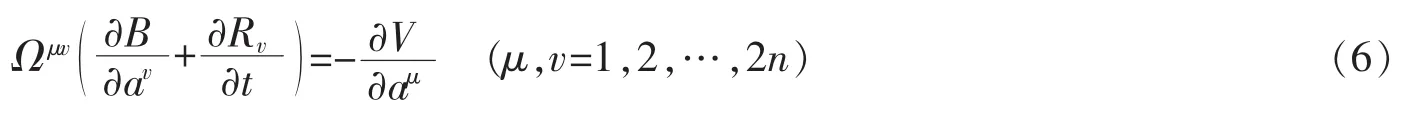
例1某二阶Birkhoff系统的Birkhoff函数和Birkhoff函数组为

这是一个非自治Birkhoff系统。

由式（7）得

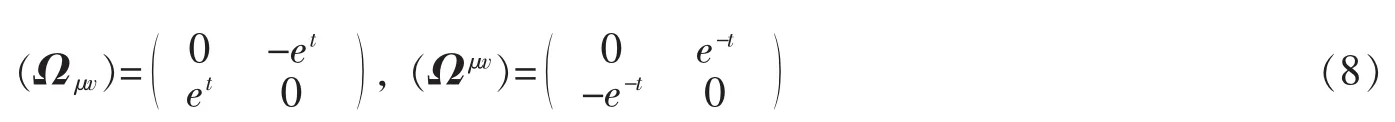
方程（3）给出

容易验证，条件（4）和（5）满足。因此，系统（7）是一个梯度系统，其势函数为

显然，V相对于变量a1是负定的，相对于变量a2是正定的。将式（10）对时间求导，并考虑到方程（9），有

3 非自治广义Birkhoff系统的梯度表示

广义Birkhoff系统的运动微分方程为[11]

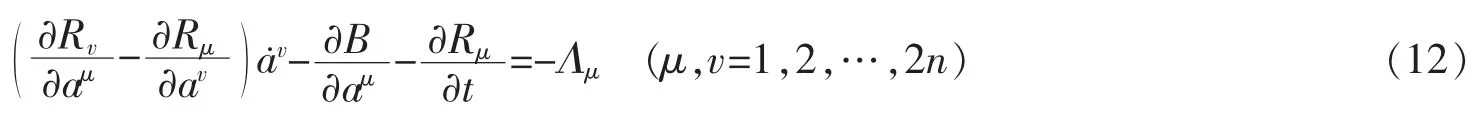
如果Birkhoff函数B，Birkhoff函数组Rμ以及附加项Λμ都显含时间t，则称为非自治的。

假设系统非奇异，则方程（12）可表为

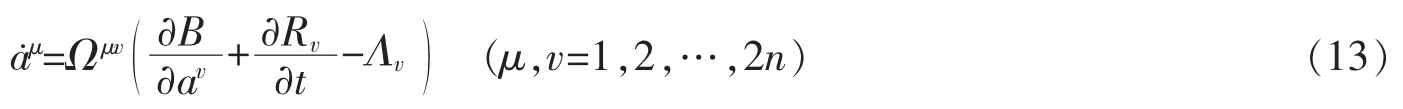
一般而言，非自治广义Birkhoff系统也不是一个梯度系统。

如果满足条件

以及

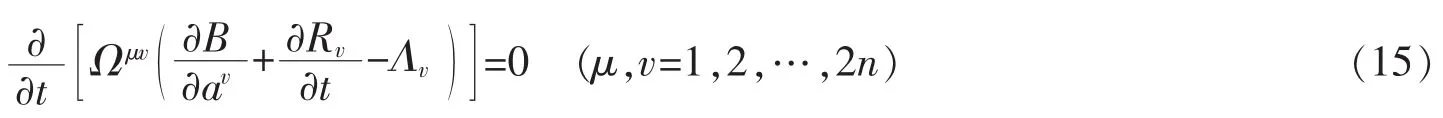
则方程（13）是一个梯度系统。此时，可找到势函数V=V（a），使得

例2二阶广义Birkhoff系统的Birkhoff函数和Birkhoff函数组为

附加项为

这是一个非自治广义Birkhoff系统。

由式（17）得

方程（13）给出

容易验证，条件（14）和（15）满足。系统（17）和（18）是一个梯度系统，由式（16）求得势函数为

求导得

由Lyapunov定理可知，零解a1＝a2＝0是渐近稳定的。

4 结语

Birkhoff系统和广义Birkhoff系统在一定条件下可化为梯度系统，这样便可利用梯度系统的性质来研究Birkhoff系统的积分和稳定性问题。以往的研究限于自治情形。文中讨论了一类非自治Birkhoff系统和非自治广义Birkhoff系统的梯度表示，算例也表明了结果的有效性。

[1]Hirsch M W，Smale S，Devaney R L.Differential Equations，Dynamical Systems and An Introduction to Chaos[M].Singapore：Elsevier，2008.

[2]梅凤翔.关于梯度系统[J].力学与实践，2012，34（1）：89-90.

[3]梅凤翔，吴惠彬.一阶Lagrange系统的梯度表示[J].物理学报，2013，62（21）：214501.

[4]楼智美，梅凤翔.力学系统的二阶梯度表示[J].物理学报，2012，61（2）：024502.

[5]梅凤翔，李彦敏.弱非完整系统的梯度表示和分数维梯度表示[J].商丘师范学院学报，2011，27（9）：1-3.

[6]梅凤翔，崔金超，吴惠彬.Birkhoff系统的梯度表示和分数维梯度表示[J].北京理工大学学报，2012，32（12）：1298-1300.

[7]梅凤翔，吴惠彬.广义Birkhoff系统的梯度表示[J].动力学与控制学报，2012，10（4）：289-292.

[8]Mei Fengxiang，Wu Huibin.Bifurcation for the generalized Birkhoffian system[J].Chinese Physics B，2015，24（5）：054501.

[9]梅凤翔，吴惠彬.广义Hamilton系统与梯度系统[J].中国科学：物理学力学天文学，2013，43（4）：538-540.

[10]梅凤翔，史荣昌，张永发，等.Birkhoff系统动力学[M].北京：北京理工大学出版社，1996.

[11]梅凤翔.广义Birkhoff系统动力学[M].北京：北京理工大学出版社，2013.

A gradient representation for a type of non-autonomous Birkhoffian systems

ZHANG Yi
（School of Civil Engineering，SUST，Suzhou 215011，China）

A gradient representation for a type of non-autonomous Birkhoffian systems is studied.The conditions under which the non-autonomous Birkhoffian system or the non-autonomous generalized Birkhoffian system can be considered as a gradient system are obtained.Two examples are given to illustrate the application of the results.

non-autonomous Birkhoffian system；gradient system；potential function；stability

O316

A

1672－0687（2015）04－0001－03

责任编辑：谢金春

2015－06－29

国家自然科学基金资助项目（10972151；11272227）

张毅（1964-），男，江苏吴江人，博士，教授，博士生导师，研究方向：分析力学，力学中的数学方法。