基于模糊模型的一类不确定非线性系统协调优化控制
郝万君,乔焰辉,李泽,许洪华,马洁明
(1.苏州科技学院电子与信息工程学院,江苏苏州215009;2.苏州科技学院机械工程学院,江苏苏州215011)
基于模糊模型的一类不确定非线性系统协调优化控制
郝万君1,乔焰辉2,李泽1,许洪华1,马洁明1
(1.苏州科技学院电子与信息工程学院,江苏苏州215009;2.苏州科技学院机械工程学院,江苏苏州215011)
以典型的不确定非线性系统——发电单元机组为例,提出了基于模糊模型的协调优化控制新方案。首先建立该系统的模糊状态空间模型,然后依据此模糊模型和极点配置技术设计了具有渐进跟踪性能的状态反馈控制器。针对此系统的非线性、参数时变、多变量耦合等特征所导致的极点配置最佳参数难以确定的问题,提出了基于改进粒子群算法(PSO)的多目标优化极点配置参数新策略,进而实现了系统的协调优化控制。仿真研究表明:依据该方法设计的协调控制系统在大范围工况下具有良好的调节品质、抗干扰能力和对参数变化的鲁棒性。
不确定非线性系统;T-S模糊模型;协调控制;多目标优化;粒子群算法
发电单元机组协调控制系统是典型的具有多输入多输出的非线性时变系统,系统参数随着运行工况的改变有较大的变化,且各变量之间存在严重的耦合,其准确模型难以建立,以PID控制为基础的常规协调控制难以获得理想的控制效果[1]。
文献[2]直接利用Bell-Astrom非线性模型中控制量与被控量之间的映射关系,分别基于粒子群优化,研究了单元机组的负荷、压力设定点跟踪问题。但当单元机组的运行偏离特定工况时,系统的瞬态性能和稳定性将无法保证。文献[3-4]基于系统典型工况点下的局部线性化模型,通过数据(或模糊)插值和极点配置方法设计了状态反馈控制律。文献依据经验或试凑法给出了一组标称工况点附近的极点配置参数,但当系统运行工况点发生变化时,依据这组参数设计的控制器不能保证具有良好地控制品质。文献[5]根据系统的I/O信息,建立机组负荷对象逆系统的模糊模型,并依据该模型提出了一种自适应解耦控制方法。文献[6]利用H∞/混合灵敏度方法设计出多个H∞局部鲁棒控制器以覆盖单元机组的负荷变化区间,然后利用免疫遗传算法对模糊增益调度准则的结构参数进行优化设计。但当机组对象的动态特性发生明显变化时该控制系统的自适应能力和鲁棒性还有待考察。
文中以笔者和前人的研究成果为基础,针对一类不确定非线性系统的控制问题,将多目标优化算法与状态反馈控制、模糊控制相结合,提出了一种基于模糊模型的协调优化控制的新方案,最后通过仿真研究验证了该方法的控制效果。
1 系统的模糊状态空间模型
1.1 系统的非线性动态描述
被控对象模型是单元机组协调控制系统分析与设计的基础。Bell-Astrom模型是一种很具有代表性的模型,该模型已被国内外的研究广泛引用[7],其动态方程组表示如下

式中:αcs为蒸汽品质系数;qe为蒸汽消耗率,kg·s-1。它们由下式计算

汽包蒸汽压力x1,kg·cm-2;输出电功率x2,MW;蒸汽水流体密度x3,kg·m-3是状态变量。汽包蒸汽压力y1;输出电功率y2;汽包水位y3,m是系统的输出。
系统输入u1、u2、u3分别是燃料门、汽轮机和给水门的调节阀开度,其幅值和变化速率受下列条件约束

uj(j=1,2,3)的上下限0、1代表阀门关死和开足。
1.2 系统的T-S模糊模型描述
考虑从该非线性系统的一组观测数据中辨识获得系统的模型参数,并转化为T-S模糊模型描述

其中,z1(t),…,zp(t)为前件变量,Mij代表模糊集合,r是规则数;x=[x1,x2,x3]T,u=[u1,u2,u3]T,y=[y1,y2,y3]T分别为系统的状态、控制、输出变量,式中A、B、C、D均是3×3维的系数矩阵。
系统的全局T-S模糊模型为
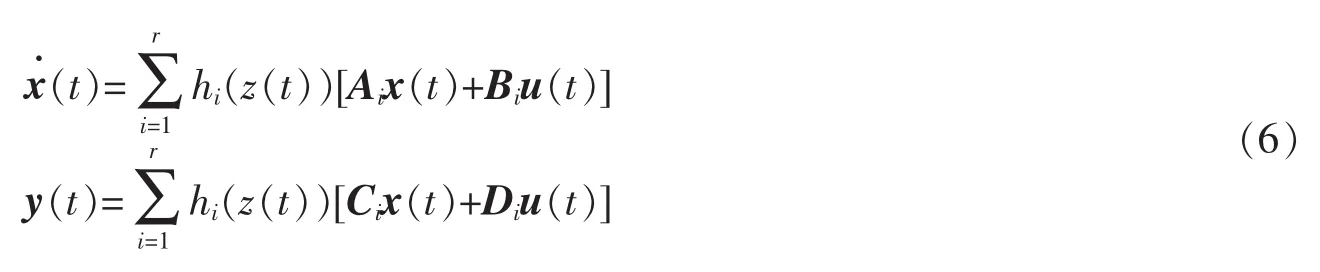
1.3 系统的增广T-S模糊模型
系统的设定值和外部扰动通常不为常值,具有阶跃信号性质,为克服给定或外部阶跃扰动影响,实现系统的无差控制,引入含积分环节的设定值跟踪控制结构,如图1所示。y、r、e分别为系统的输出、设定和偏差,η为新增的状态变量;ui为积分控制输出,uf为状态反馈控制,K1为反馈控制增益,K2为积分器增益。

图1 设定值跟踪PDC控制系统结构框图
设系统的跟踪误差为:e(t)=r(t)-y(t),对跟踪误差积分可得到
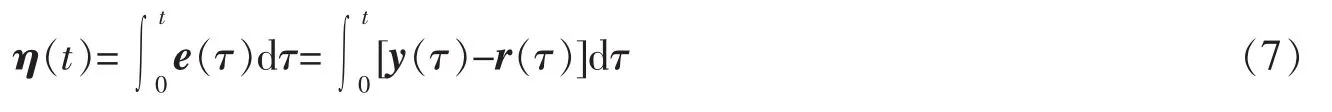
令y′(t)=η(t),将η作为附加的状态向量引入式(5),进而构造增广系统的状态方程

经过fuzzy推理,增广系统的最终输出为

笔者在前期工作中,基于模糊自适应竞争聚类和最小二乘递推算法,利用单元机组的实验数据,以汽包蒸汽压力为前提变量,建立了系统在70%、80%、90%、100%、110%、120%、130%等7个典型工况点下的T-S模糊子空间模型,具体模型及参数可参见文献[8]。
2 协调优化控制器设计
2.1 并行分布补偿(PDC)控制器设计
设Ci表示第i个子系统对应的控制器,即:

ui是根据式(9)对第i个线性化模型进行极点配置得到的渐近跟踪控制器的输出。
全局控制输出为各个局部控制器模糊加权
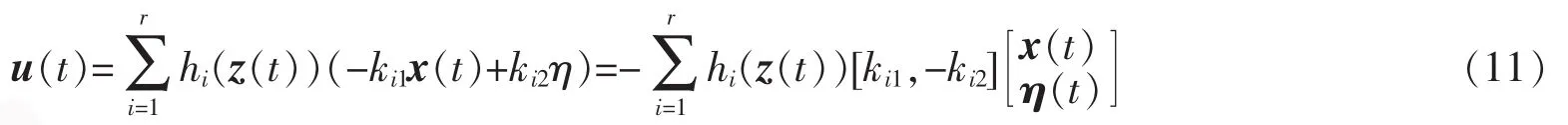
2.2 系统的稳定性分析
对于式(9)所建立单元机组协调系统的T-S模糊控制模型,利用式(11)所设计模糊状态反馈控制律,针对此系统进行稳定性分析。
定理1对于式(9)所述的模糊控制系统,闭环大范围渐近稳定的条件是存在共同的正定矩阵P,满足
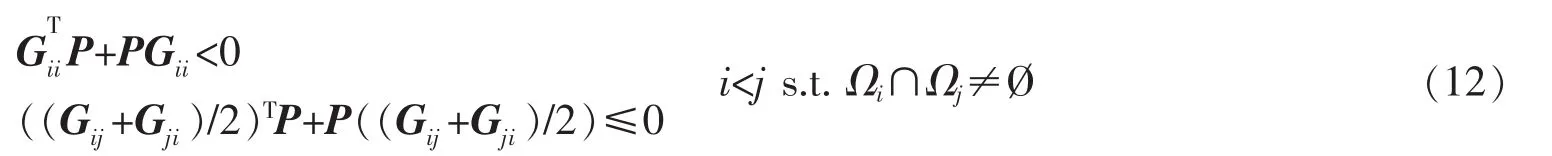
3 控制器参数的多目标优化
3.1 控制系统的多目标优化函数定义
控制系统的极点配置参数优化本质上是基于给定目标函数的参数寻优问题。目标函数和约束条件的选择是决定算法优化效果的关键因素。为此,笔者提出了在满足稳定性和控制量约束前提下的控制性能多目标优化函数
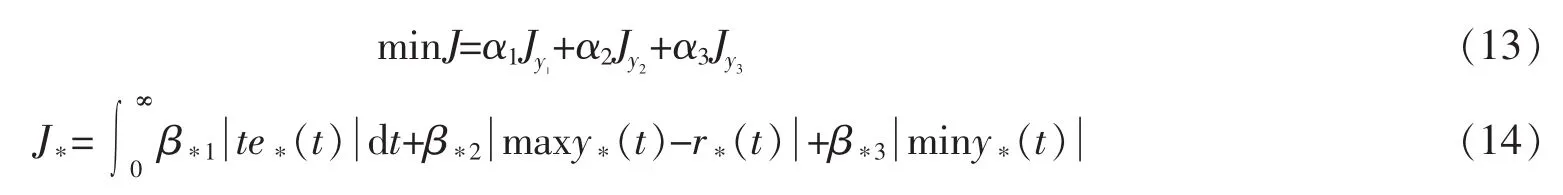
3.2 改进的PSO寻优算法
PSO优化算法[10]中,每个优化问题的解都是N维目标搜索空间中的一个粒子,共有m个粒子组成一个群体。每个粒子性能的优劣程度取决于待优化问题目标函数,每个粒子由一个速度决定其飞行的方向和速率的大小,粒子们追随当前的最优粒子在解空间中进行搜索。PSO初始化为一群随机粒子(随机解),然后通过迭代找到最优解。在每次迭代时,粒子通过跟踪两个最优解来更新自己,最终达到从全空间搜索最优解的目的。在第k次迭代时粒子i的位置、飞行速度可以分别表示为

第一个就是粒子本身所找到的最优解,即个体极值pBest,可以表示为

另一个极值是整个种群目前找到的最优解,即全局极值gBest,可以表示为

在第k+1次迭代计算时,粒子i根据下列规则来更新自己的速度和位置

c1,c2是学习因子,为非负常数;r1、r2是介于[0,1]之间两个独立的随机数;n=1,2,…,N;Xin∈[xminn,xmaxn],根据实际问题来确定粒子取值范围;vin∈[-vmaxn,vmaxn],单步前进的最大值vmaxn根据粒子取值区间长度来确定。
w是惯性权值,是影响粒子全局或局部搜索能力与速度的关键参数。文中提出的改进算法区别于常规PSO算法,惯性权值w不随迭代次数k的线性变化,而是与PSO寻优收敛速度相关的函数,计算公式为

式中w(k)、wmax、wmin分别为当前时刻的惯性权重、最大权重、最小权重;Jopt、Jmean是当前时刻全局最优粒子的适应度函数及所有粒子适应度函数的平均值。
如此设计的目的是为了使惯性权值w能够随着PSO寻优进程而自适应调整,而与迭代次数k无关,这样即提高PSO算法收敛速度,保证算法的实时性,不容易陷入局部最优,同时避免了通常按迭代次数线性减小w的方法中,因不适当地选取最大迭代次数(kmax)造成对w的不合适的选择。
3.3 极点配置参数寻优和反馈控制律求解
4 仿真研究
PSO的参数设置:种群总数60,微粒维数为6(对应δ1,δ2,…,δ6,6个极点配置参数),最大迭代次数100,c1=c2=1.5,wmax=0.95,wmin=0.1。
通过PSO多目标优化最终获得的极点配置参数为

对所设计的单元机组控制策略进行仿真检验,假设在t=0时刻系统稳定地工作在标称工作点,参考输入采用文献[4]中给定的信号

即在t=200 s时,汽包压力的参考输入由108 kgf/cm2阶跃到120 kgf/cm2;在t=600 s时,输出功率的参考输入由66.65 MW阶跃到120 MW;汽包水位的参考输入保持在0 m;式中1(t-t0)是单位阶跃函数。
图2为文中方法与文献[4]方法的比较曲线。从对比曲线可以看出,在系统调解的快速性方面,文中方法的汽包压力(P)、功率输出(P0)和汽包水位(L)参数都能以比文献[4]更快的速度跟踪设定值变化,使系统的动态调节过程大大缩短;在超调量方面,对于汽包压力和功率输出2个参数两种方法在都基本没有超调。在汽包水位超调方面文中方法比文献[4]略大,两个最大超调点的数值分别为-0.018 2 m和0.033 2 m,也都在系统允许范围内。若按汽包水位偏差小于0.001 m算作进入稳态,经过汽包压力和功率输出两次设定值扰动后文中方法比文献[4]分别提前68 s和153 s进入稳态;在稳定性和鲁棒性方面,随着输入信号的阶跃变化,系统的状态和输出已经大大地偏离了原先的工况点,此时单元机组的参数已经发生很大的改变,但控制系统的输出依然能够很快达到稳定,体现了该控制策略具有很好的鲁棒稳定性;应用文献[4]方法仿真,其总目标函数J的数值为5.479 3e+004,完全相同的实验条件下,文中方法的总目标函数值仅为3.050 2e+004,可见性能远优于比较文献。
由图3可知,燃料门调节阀开度(u1)、汽轮机调节阀开度(u2)和给水流量调节阀开度(u3)等3个控制量的变化过程平稳,其变化速率满足式(4)所示的约束条件。

图2 系统输出响应曲线

图3 调节阀开度变化曲线
5 结语
文中针对一类不确定非线性系统的控制问题,通过构建评价系统动态、稳态性能等项指标的多目标函数,提出基于模糊模型的协调优化控制策略,具有良好的无差跟踪、参数变化鲁棒性和抗干扰能力。但应注意到,由于需要优化的参数较多,且每组参数的单步仿真时间较长,导致整个优化过程耗时较多,因此,如何简化参数的优化过程,提高优化算法的实时性将是未来研究的重要课题。
[1]栾秀春,李士勇,吴建军,等.基于模糊状态观测器的单元机组T-S模糊协调控制系统[J].中国电机工程学报,2006,26(4):76-81.
[2]Jin S Heo,Kwang Y Lee,Raul Garduno-Ramirez.Multi-objective control of power plants using particle swarm optimization techniques[J].IEEE Transactions on Energy Conversion,2006,21(2):552-561.
[3]Huang Zuyi,Li Donghai,Jiang Xuezhi,et al.Gain scheduled servo system for boiler-turbine unit[J].Proceedings of the CSEE,2003,23(10):191-198.
[4]栾秀春,李士勇,张宇.单元机组的T-S模糊协调控制系统极其LMI分析[J].中国电机工程学报,2005,25(19):91-95.
[5]王志杰,王广军,陈红.基于逆模型的火电机组自适应解耦控制[J].中国电机工程学报,2011,31(29):118-123.
[6]林金星,沈炯,李益国.基于免疫优化的机炉协调系统模糊增益调度H∞鲁棒控制[J].中国电机工程学报,2008,28(17):92-98.
[7]Li Chaoshun,Zhou Jianzhong,Li Qingqing,et al.A new T-S fuzzy-modeling approach to identify a boiler-turbine system[J].Expert Systems with Applications,2010,37(3):2214-2221.
[8]郝万君,乔焰辉,关尚军.基于自适应竞争聚类的多输入多输出热工过程模糊辨识[J].动力工程学报,2012,32(10):798-803.
[9]Tanaka K.Wang H O.Fuzzy Control Systems Design and Analysis:A Linear Matrix Inequality Approach[M].New York,USA:John Wiley&Sons Inc,2001.
[10]Kennedy J,Eberhart R C.Particle swarm optimization//[C]Proc IEEE International Conference on Neural Networks,Perth,Australia,1995:1942-1948.
Coordination optimization control of a class of uncertain nonlinear system based on fuzzy model
HAO Wanjun1,QIAO Yanhui2,LI Ze1,XU Honghua1,MA Jieming1
(1.School of Electronic&Information Engineering,SUST,Suzhou 215009,China;2.School of Mechanical Engineering,SUST,Suzhou 215011,China)
Taking the typical uncertain nonlinear system as an example,a new scheme of Coordination Optimization Control based on fuzzy model is proposed.Firstly,a fuzzy state space model of boiler-turbine system was built.Then,based on the model and pole placement design,a state feedback controller with asymptotic tracking performance was proposed.Because the system had nonlinearity,multivariable coupling and parameter timevarying which made the optimum parameters of pole placement difficult to determine,a multi-objective optimization method for pole placement based on particle swarm optimization was given.And the coordination optimization control of the system was realized.Simulation results show that the system designed with the proposed method demonstrates satisfactory regulation quality,anti-interference ability and robustness against parameter variations within wide operating range.
uncertain nonlinear system;T-S fuzzy model;coordinated control;multi-objective optimization;particle swarm optimization
TP272;TK323
A
1672-0687(2015)04-0040-06
责任编辑:艾淑艳
2015-01-18
国家自然科学基金资助项目(51477109;61203048);住房与城乡建设部项目(2014-K1-040;2014-K6-007)
郝万君(1965-),男,吉林吉林人,教授,博士,研究方向:复杂系统建模,智能控制,优化控制。

