低含沙水流圆柱和方柱绕流水动力特性

孙　壮，龚希武，高　杰

(浙江海洋学院 船舶与海洋工程学院，浙江　舟山　316022)



低含沙水流圆柱和方柱绕流水动力特性

孙壮，龚希武，高杰

(浙江海洋学院 船舶与海洋工程学院，浙江舟山316022)

摘要：为了研究低含沙水流中钝体绕流的水动力特性，基于FLUENT软件的DPM模型对亚临界雷诺数下二维钝体绕流进行数值模拟仿真。本文首先由清水实验得到平均阻力系数Cd，在清水的基础上加入DPM模型，探究低浓度悬浮颗粒对Cd的影响。研究表明，加入低含量直径0.1 mm的泥沙颗粒后，圆柱和方柱的Cd有显著增长趋势。而方柱仍对含沙量更敏感，单位体积含沙量的Cd增长率大于圆柱。圆柱在1%~4%含沙量水流中单位含沙量Cd增长率为0.45%~1.62%，增长平缓，含沙量增至4%~8%Cd增长率提升至1.29%~3.14%,增长相对剧烈;相应地，方柱的Cd增长率则由2.85%~4.31%提升至3.28%~4.56%，说明低含沙水流中圆柱和方柱Cd的增长规律与含沙量并非线性关系。

关键词：低含沙水流；亚临界雷诺数；阻力系数；DPM模型

钝体在一定的流速下，会在物体两侧交替产生脱离结构物表面的漩涡。钝体绕流现象普遍存在于工程实践中，如桥墩绕流、跨海大桥桥塔绕流等，当涡街发生时，交替产生的漩涡脱落诱发交变力，严重时产生共振及声振，对结构物正常使用造成了极大的威胁[1]。目前已有诸多学者对圆柱和方柱绕流进行过研究。Zhang[2]等采纳LES模型分析了Re=3 900圆柱的受力，论证有限长圆柱的升阻力系数低于无限长圆柱。Sunghan[3]等利用3D LES方法计算圆柱的水动力和压力系数，探究了Re=5 500~41 300圆柱尾迹和剪切层不稳定性。Akhilesh[4]等模拟了二维非定常幂律流体在低雷诺数Re=60~160幂律指数0.5~2下方柱涡脱落的流场结构，以及得到平均压力阻力系数，总阻力系数，升力系数均方根值等流场参数。

自然界的河流、近海水道中常常携带着泥沙，含沙水流实验成果表明，与相同条件的清水水流相比，水流的时均结构和脉动结构的确发生了相应的变化。由长江入海口以及杭州湾输运而来的泥沙导致舟山群岛海域悬浮泥沙颗粒浓度约0.2~0.5 g/L，属于低含沙水流。Liu[5]等建立低含沙水流基于两相流理论，提出曲线网格中数学模型的解决方案，并与长江的实测资料水位、流速、河床形变相符。刘超[6]综述了前人高低含沙水流的研究成果，论述了挟沙水流流速分布、紊动强度和阻力特性三方面的特征规律。目前学者对高含沙水流研究成果较多，而低含沙水流下钝体绕流的水动力特性研究相对匮乏。因此，研究低含沙水流有重要的理论意义和工程价值。

1基本方程

令水流中悬移质泥沙体积含量为φ，清水体积含量c=1-φ。在直角坐标系下，对二维粘性流体建立含沙水流方程。

(1)连续性方程

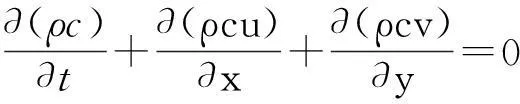
(1)

(2)运动方程

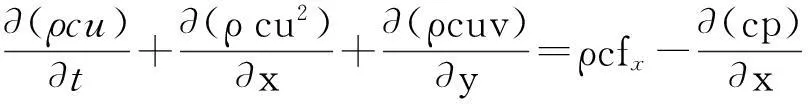
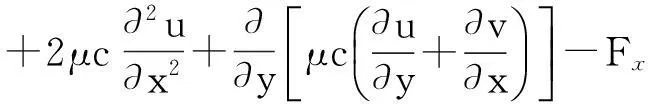
(2)

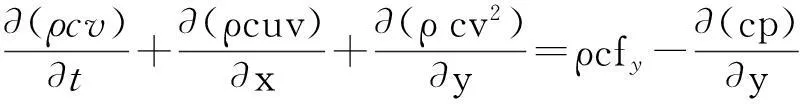
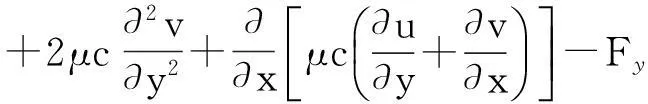
(3)

式中u、v——x、y方向的速度;

p——压强;

μ——流体的动力粘性系数；

fx、fy——表示作用在 流体单元上单位质量的体积力在x、y方向的分量；

Fx、Fy——水流作用在沙粒上的相间作用力，主要包括相间阻力和浮力。

2数值方案

一般定义边界层内流速达到来流流速的99%为界层的边缘[7]。在钝体绕流问题中精确地模拟壁面边界层对于结果的准确性至关重要，计算区域网格采用分块的结构化网格，钝体周围计算区域为“O”型网格(图1、图2)。该模型计算域大小取为30D·20 D，D表示圆柱和方柱的特征长度，圆柱和方柱上游断面距离圆柱体心10 D，下游断面距离圆柱体心20 D。

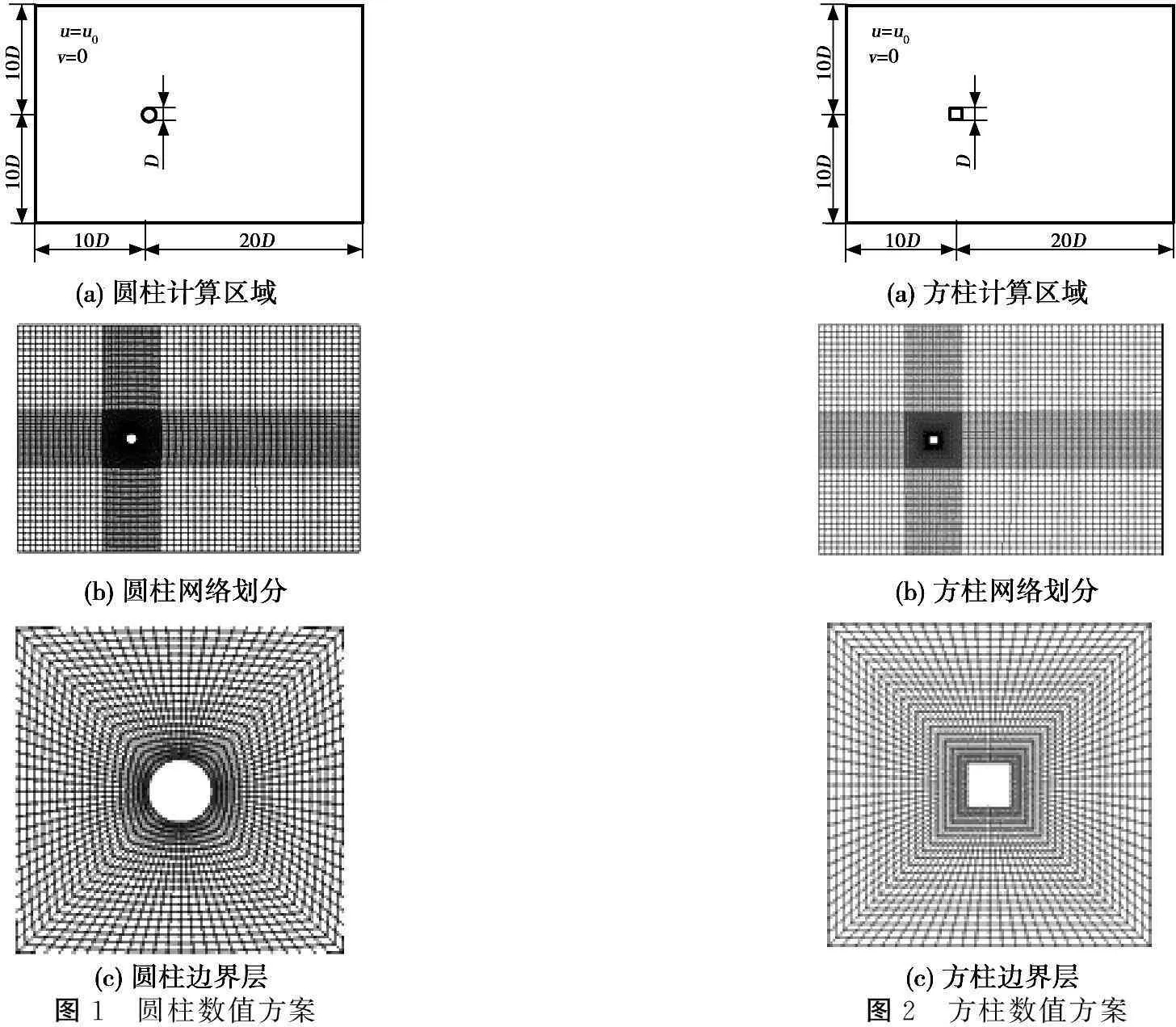
图1 圆柱数值方案图2 方柱数值方案

湍流模型选定Realizablek-ε，低含沙水流中，FLUENT提供精度高于Eulerian Model的离散相模型(DPM——Discrete Phase Model)，该模型假定离散相非常稀薄，体积率一般不超过10%~12%。本文中泥沙颗粒的直径为0.1 mm，密度1 800 kg/m3，分别计算体积含沙量分别为1%、4%和8%水流下圆柱和方柱的水动力参数。

本文研究的是二维绕流数值模拟，Re=200时采用层流模型，Re>=3 000时采用Realizablek-ε湍流模型。计算域边界条件设置如下:

3结果与分析

计算得到圆柱和方柱在雷诺数Re=200、3 000、5 000、8 000和10 000五种工况下钝体绕流的平均阻力系数Cd。在含沙水流研究中，设定含沙量φ=1%、4%和8%三组方案探究含沙量对Cd的影响。现将各组计算结果整理如表1。

表1圆柱和方柱绕流FLUENT数值模拟结果

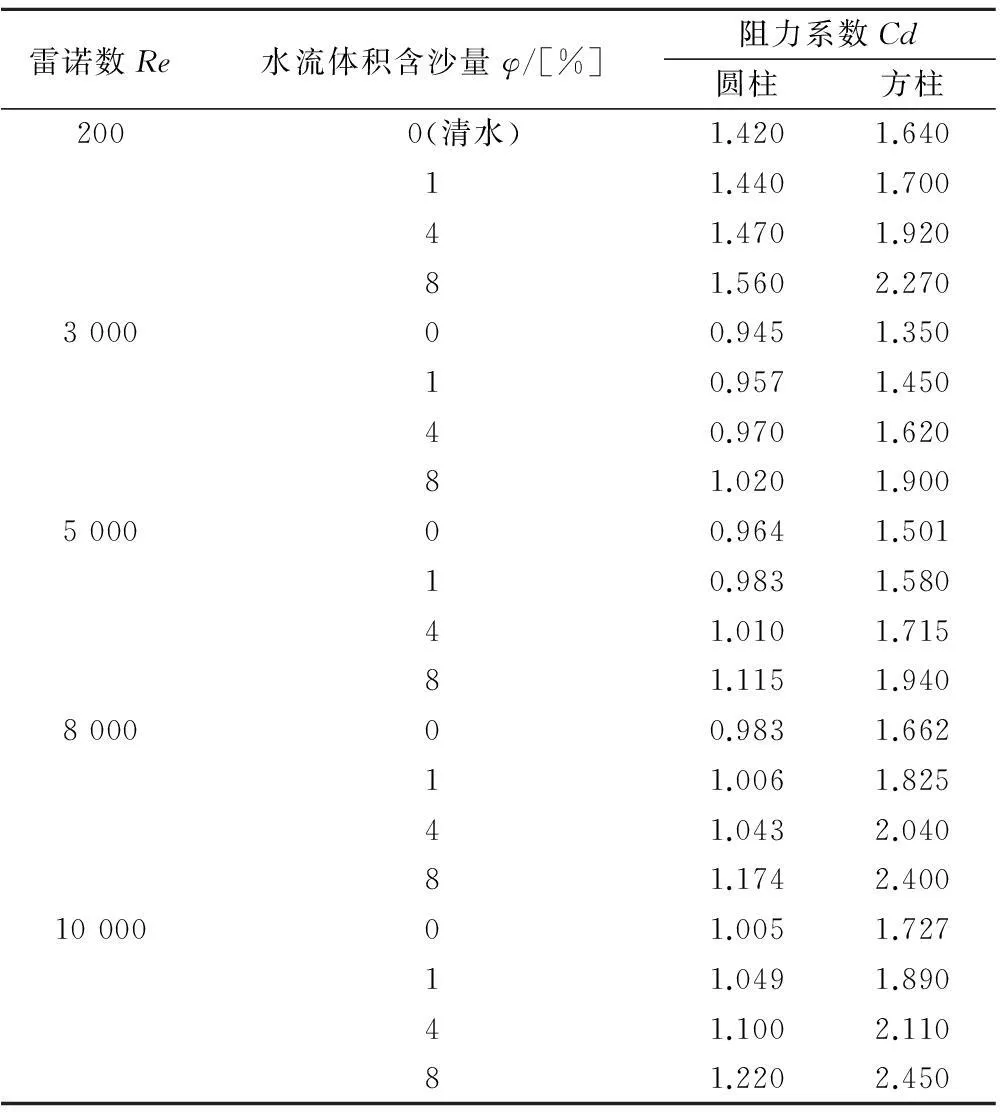
雷诺数Re水流体积含沙量φ/[%]阻力系数Cd圆柱方柱200 0(清水)1.4201.64011.4401.70041.4701.92081.5602.270300000.9451.35010.9571.45040.9701.62081.0201.900500000.9641.50110.9831.58041.0101.71581.1151.940800000.9831.66211.0061.82541.0432.04081.1742.4001000001.0051.72711.0491.89041.1002.11081.2202.450

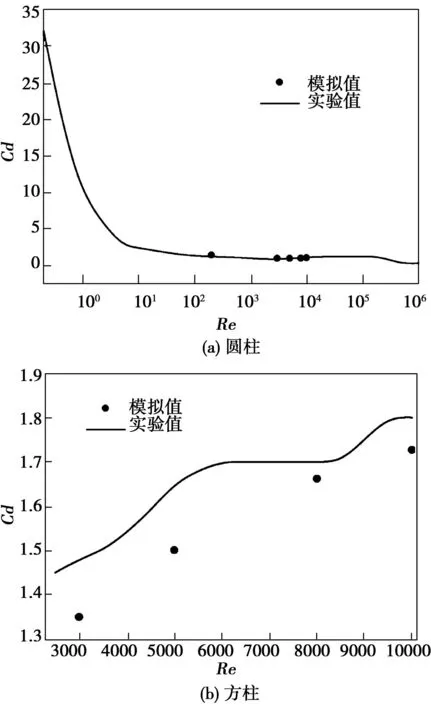
图3　Cd-Re曲线

表1给出了FLUENT软件在亚临界雷诺数Re=200~10 000下圆柱和方柱绕流的Cd。为验证数值模拟的准确性，将清水条件下圆柱绕流的FLUENT模拟结果同实验值对比。如图3(a)所示，圆柱数值模拟的计算结果与图中实验值吻合，变化趋势也基本一致，从而证明本文计算方法的有效性和可靠性。

图3(b)中，方柱的模拟值在Re=3 000~10 000范围内与实验值趋势保持一致，Cd普遍略小。这是因为复杂的湍流流态引发强烈的脉动，考虑不确定因素的干扰，偏差势必存在。其中，最大偏差不超过10%，在可接受范围内，不影响结论。

3.1　清水中圆柱与方柱绕流

绕流物体受到总的粘性阻力由两部分组成：摩擦阻力和形状阻力，分别是与物面上相切的剪应力和垂直于物面的压力在来流方向的合力。本文研究的水动力参数主要是Cd，分别选取圆柱和方柱层流状态Re=200以及湍流状态Re=8 000、10 000进一步分析Cd-t曲线。

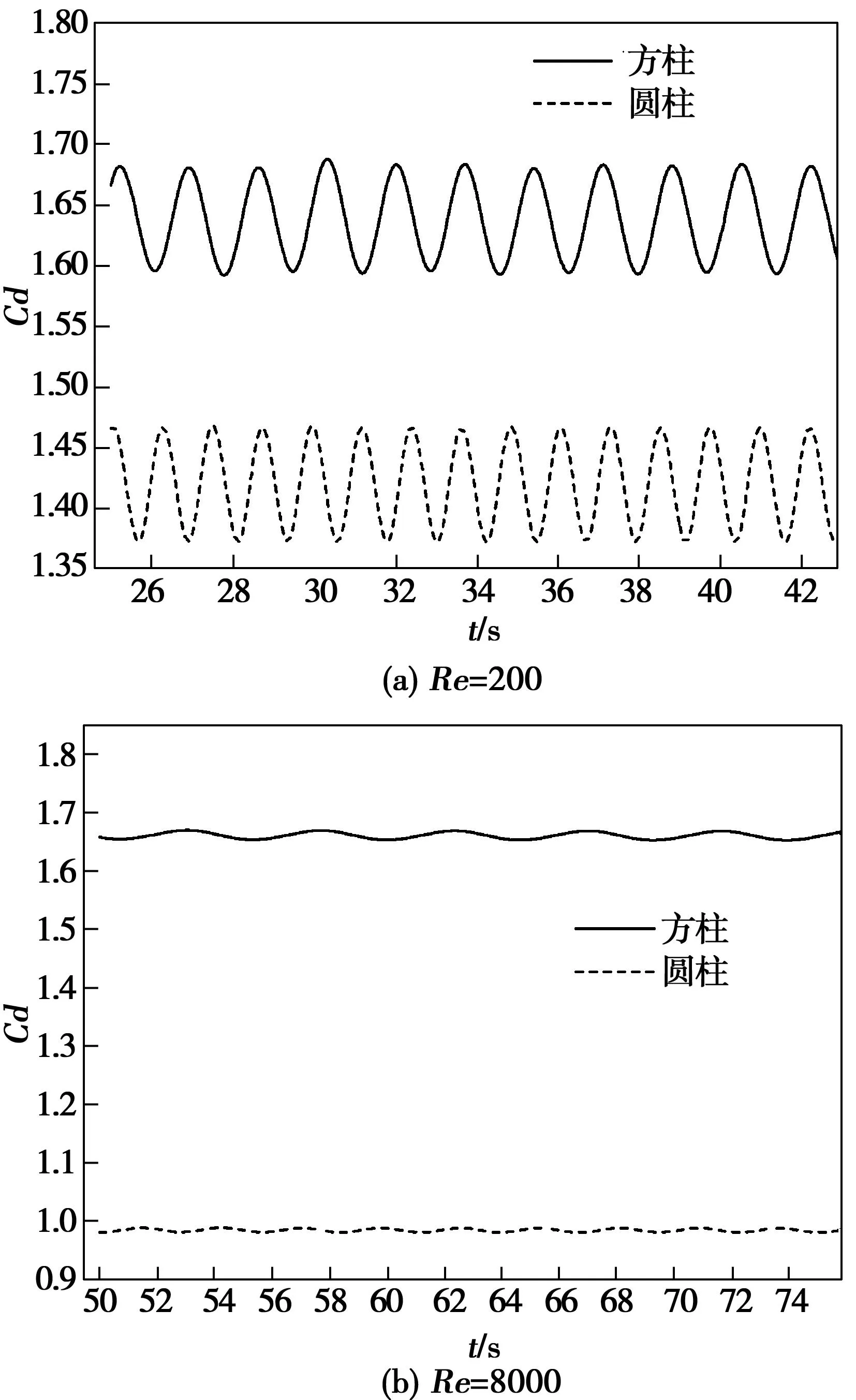
图4　不同雷诺数Cd-t曲线

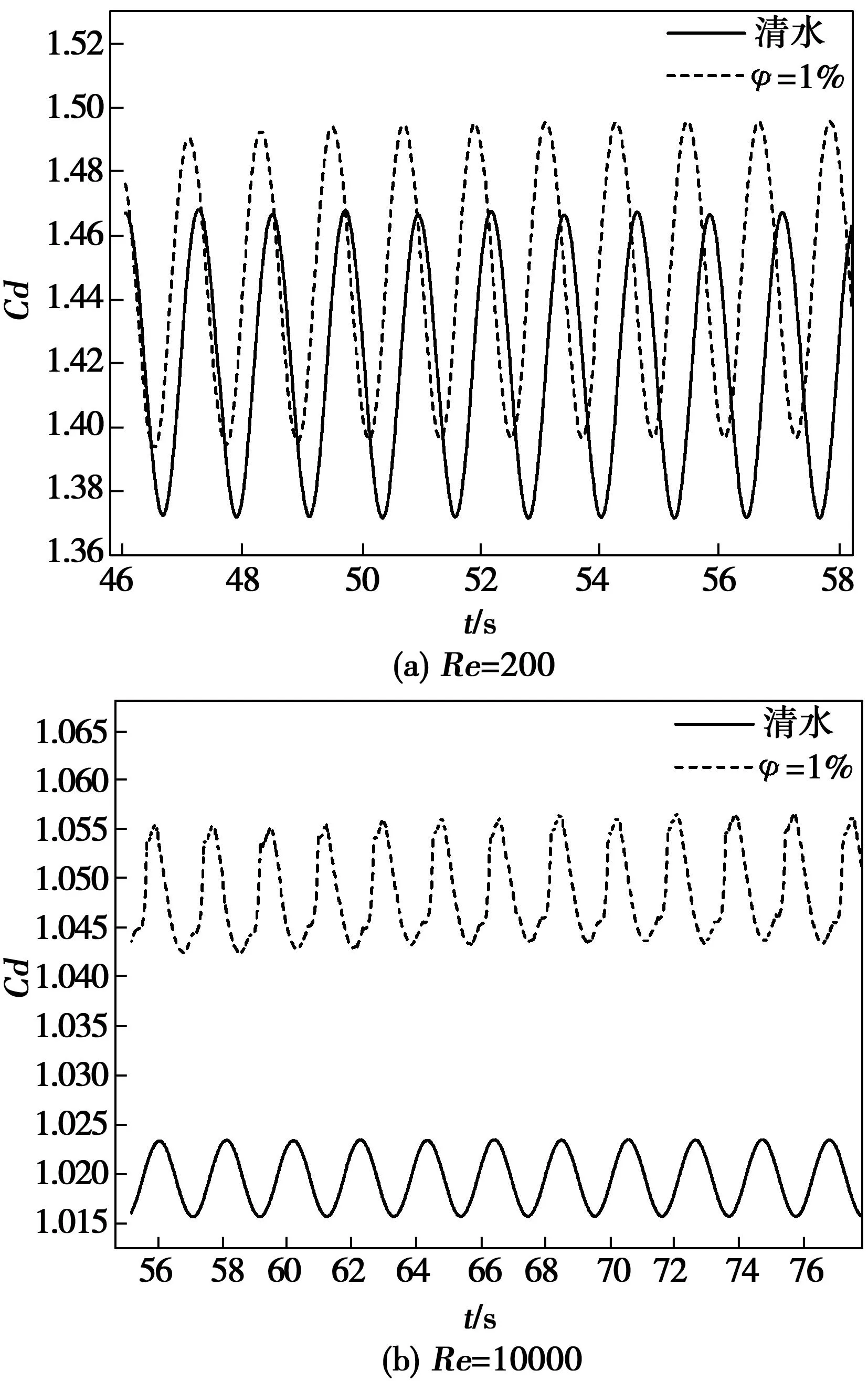
图5　不同雷诺数下圆柱加沙的Cd-t曲线

如图4(a)、图4(b)所示，层流及湍流清水中方柱和圆柱表面的阻力都呈规则的周期性振荡规律。相同雷诺数下，方柱绕流的阻力系数Cd数值明显大于圆柱。Re=200，方柱绕流漩涡脱落周期约1.69 s，圆柱约1.23 s；Re=8 000，方柱绕流漩涡脱落周期约4.68 s，圆柱约2.76 s，可见方柱漩涡脱落周期大于圆柱。由涡脱落的周期推算出频率，依据水中结构自振频率，我们能够选择恰当的截面形状、尺寸减弱共振，规避风险。

3.2　清水与含沙水流

舟山群岛海域水道一般挟带疏散泥沙颗粒，不能视为连续介质的液体。沙粒超前或滞后于水流质点速度，引起沙粒纷纷从流线上脱落，从而把水流分解成不连续的两相流动。颗粒运动方向大致与水流一致，但是颗粒本身作为刚体，受到惯性、接触碰撞，以及动量传递等多因素的影响，比仅以水为对象的一相流复杂得多，并具有它的本质特点[8]。

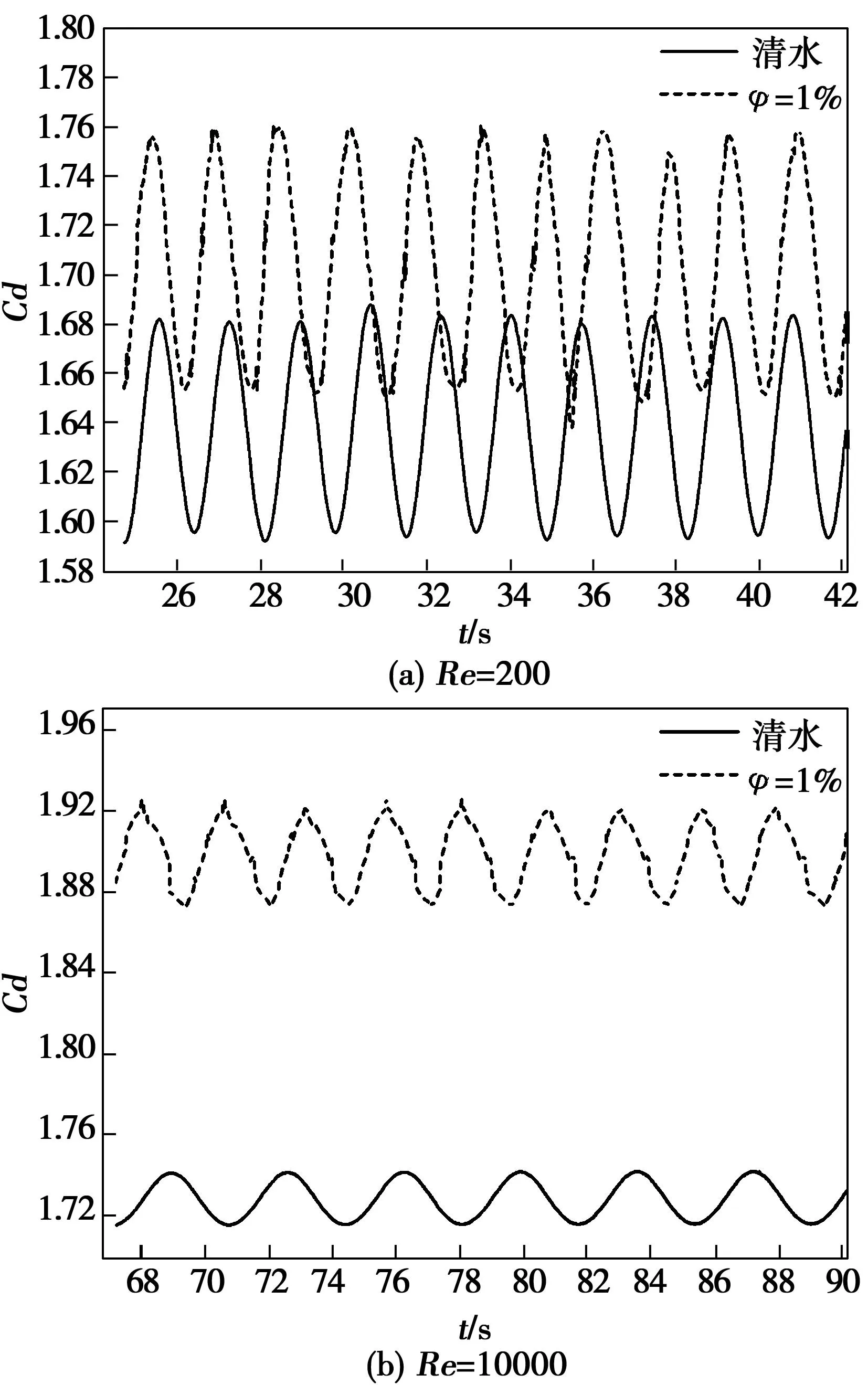
图6　不同雷诺数下方柱加沙的Cd-t曲线

图5(a)、图5(b)、图6(a)和图6(b)中φ表示含沙水流中泥沙颗粒的体积含量。如图所示，含沙水流中，Cd-t周期性曲线出现微小的波动。相对于清水，含沙水流中圆柱和方柱的阻力系数Cd均出现不同程度增加。以Re=10 000为例，清水中加入1%体积含量的泥沙颗粒后，圆柱的Cd增长4.38%，而方柱的Cd增长9.44%。可见，泥沙对于方柱绕流阻力的影响更明显，增幅更大。因此在多沙海域水道，应适当加强水下结构物材料的强度，尤其是方柱迎流面等主要受力部位。

分析水中泥沙颗粒增大阻力系数的原因：水流运动时，将带动其周围泥沙颗粒同向运动，颗粒本身相对于水体而言不易变形，对流动的水体起阻尼作用，实质上增大了液体的粘性[8]。流体粘性增大，由牛顿内摩擦定律可知，剪切应力正比于动力粘性系数，因此摩擦阻力增大。形状阻力是由粘性消耗水质点的动能形成前后压力差而产生的，粘性对流体的阻滞越强，首尾压力差越大，形状阻力越大。摩擦阻力和形状阻力的联合作用促使柱体阻力增大。

3.3　体积含沙量的影响

前文我们讨论了挟沙水流中圆柱和方柱阻力系数Cd有所增长。现在泥沙量由1%增至4%、8%，深入研究泥沙量对阻力特性的影响。

图7(a)、图7(b)、图8(a)和图8(b)给出了不同含沙量下圆柱和方柱阻力系数的振荡曲线。整体上看，水流中颗粒浓度增加，圆柱和方柱的阻力系数均持续增长。含沙量越高，Cd就越大，振幅也越大。

由图9(a)、图9(b)能够看出，水流含沙量较低时，阻力系数微弱增长，Cd-φ曲线斜率相对平缓；含沙量较高时，Cd-φ曲线斜率更陡，即阻力系数增长更快。显然，阻力系数的增长规律与含沙量并非线性关系。

表2 阻力系数与含沙量的规律

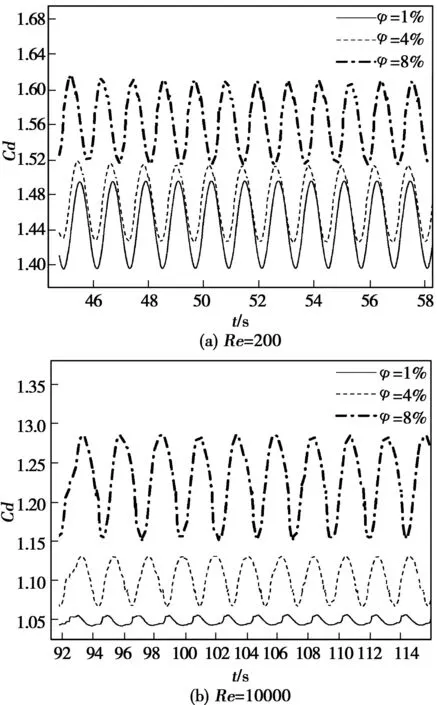
图7　不同雷诺数不同加沙量圆柱的Cd-t曲线

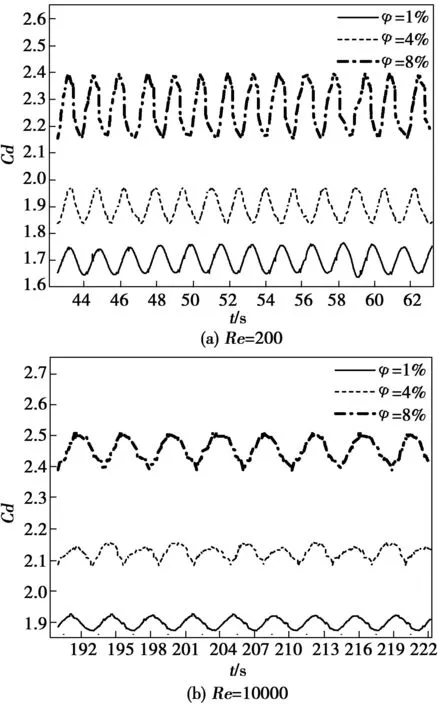
图8　不同雷诺数不同加沙量方柱的Cd-t曲线

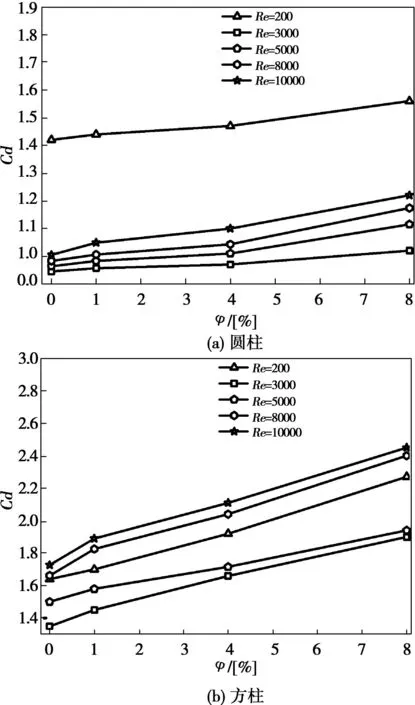
图9　不同雷诺数的Cd-φ曲线

定义相邻含沙量Cd增长率与含沙量之差的比值为单位含沙量Cd平均增长率。表2列出了低含沙水流中圆柱和方柱Cd在不同含沙量的Cd平均增长率。综合图9(a)、图9(b)以及表2，不难发现，清水中加入1%体积的泥沙后，圆柱和方柱Cd均骤然增长，圆柱的增长率为1.27%~4.38%，圆柱为3.66%~9.44%,同时二者体现出低雷诺数时增长率较小，高雷诺时增长率较大的趋势，Re=10 000增长率达到峰值。含沙量介于1%~4%之间时，圆柱单位含沙量的平均增长率为0.45%~1.62%，方柱为2.85%~4.31%，增长率有所减缓。含沙量介于4%~8%之间时，圆柱单位含沙量的平均增长率为1.29%~3.14%，方柱为3.28%~4.56%，增长率高于含沙量1%~4%水流。这是由于水流含沙量越高，颗粒间的碰撞、动量交换越频繁，相互作用越复杂，以及颗粒相增强连续相的紊动效应导致的。

我们发现相同雷诺数、相同含沙量水流中，方柱Cd值高于圆柱，Cd增长率也高于圆柱。其中，圆柱Cd增长率在含沙量1%~4%水流中较低，在含沙量4%~8%上升较大；而方柱在两种含沙量下Cd增长率相对稳定，含沙量高时Cd增长率略微上浮。

4结论

运用FLUENT软件，通过对清水和低含沙水流中亚临界雷诺数的单圆柱和单方柱绕流进行数值模拟与对比分析，本文得出以下结论：

(1)数值模拟中网格的精度与划分方式对计算结果至关重要。为得到准确的阻力系数，圆柱和方柱周围计算区域为致密的分块结构化“O”型网格；为得到清晰的涡街，需要对尾涡流场网格加密。

(2)相同亚临界雷诺数、相同含沙量下，圆柱和方柱的Cd均增加，而含沙水流对方柱的影响更显著，方柱的Cd大于圆柱，并且Cd增长率也高于圆柱。

(3)低含沙水流中，随着泥沙浓度的增加，圆柱和方柱的Cd正相关增长。圆柱Cd增长率在含沙量1%~4%水流中较低，在含沙量4%~8%上升幅度较大；而方柱在两种含沙量下Cd增长率相对稳定，含沙量较高时Cd增长率略微上浮，说明阻力系数的增长规律与含沙量并非线性关系。

参考文献

[1]刘子俊,卜京,孙健,等.建筑物尾流区风资源利用的数值模拟[J].电网与清洁能源,2014,30(9):78-82.

[2]Zhang Hui.Large-eddy Simulation of the Flow Past Both Finite and Infinite Circular Cylinders at Re=3900[J]. Journal of Hydrodynamics,2015,27(2):195-203.

[3]Sunghan Kim,Philip A. Wilson, Zhi-Min Chen. Large-eddy Simulation of the Turbulent Near Wake Behind a Circular Cylinder: Reynolds Number Effect[J]. Applied Ocean Research,2015(49):1-8.

[4]Akhilesh K. Sahu, R.P. Chhabra, V. Eswaran. Two dimensional Unsteady Laminar Flow of a Power Law Fluid Across a Square Cylinder[J]. Journal of Non-Newtonian Fluid Mechanics,2009(160):157-167.

[5]Liu Shihe, ZHAO Shilai, LUO Qiushi. Simulation of Low Concentration Sediment Laden Flow Based On Two-Phase Flow Theory[J].Journal of Hydrodynamics,2007,19(5):653-660.

[6]刘超，杨克君，赵红旭，等.河道挟沙水流特性研究进展[J].中国水运，2009(2)：48-49.

[7]盛振邦，刘应中.船舶原理(上册)[M].上海：上海交通大学出版社，2003.

[8]张瑞瑾.河流泥沙动力学[M].北京：中国水利水电出版社，2008.

Hydrodynamic Characteristics of Circular Cylinder and Square Cylinder in Sediment-laden FlowSUN Zhuang,GONG Xi-wu,GAO Jie

(School of Naval Architecture and Ocean Engineering, Zhejiang Ocean University,Zhoushan 316022,China)

Abstract：In order to investigate hydrodynamic characteristics of bluff body flow in sediment-laden flow, flow past a bluff body is simulated by two dimensional numerical simulation at a range of subcritical Reynolds numbers adopting DPM model of FLUENT software. Firstly, average drag coefficient Cd is obtained from the clear-water experimental. Then effect of low concentration suspended particles on Cd is researched via DPM model on this basis. This work demonstrates that after adding low concentration sediments whose diameter is 0.1 mm into clear-water,Cd of both square cylinder and circular cylinder have significant growth trend. Square cylinder is more sensitive to sediment concentration, and its Cd growth rate per unit volume fraction sediment is greater than circular cylinder. Cd growth rate of circular cylinder has a relatively small increase from 0.45% to 1.62% in sediment-laden flow when sediment volume fraction is from 1% to 4%. While Cd growth rate of circular cylinder has a relatively greater increase from 1.29% to 3.14% when sediment volume fraction is from 4% to 8%. Accordingly,Cd growth rate of square cylinder increases respectively from 2.85% to 4.31 and from 3.28% to 4.56%. Results indicate that Cd growth law of square and circular cylinder have a nonlinear relationship with sediment concentration.

Key words：sediment-laden flow; subcritical Reynolds number; drag coefficient; DPM model

作者简介：孙壮(1989~)，男，硕士研究生，研究方向为潮流能水轮机水动力特性。

基金项目：国家自然科学基金(No.51179174)；浙江省自然科学基金((No.Y5100180)。

收稿日期2015-04-05修订稿日期2015-07-28

中图分类号：TV143

文献标识码：A

文章编号：1002-6339 (2015) 06-0489-06