动态Bertrand模型的复杂现象与混沌控制
姚洪兴, 王 梅
(1 江苏大学 财经学院; 2 理学院, 江苏 镇江 212013 )
动态Bertrand模型的复杂现象与混沌控制
姚洪兴1,王梅2
(1江苏大学财经学院;2理学院,江苏镇江212013)
摘要:建立了基于特定需求函数的Bertrand双寡头垄断模型,分析了垄断市场下生产同质产品的企业竞争现象。应用有限理性法和不完全信息法实现了竞争模型由静态到动态的转化过程。进一步求解了动态模型的价格均衡解,并分析了均衡点的稳定状态。针对模型中出现的复杂现象提出了不同的混沌控制法,实现了垄断市场由混乱到稳定的回归。
关键词:Bertrand模型;有限理性;不完全信息;分叉;混沌
MRsubjectclassification:91B26
Bertrand模型由法国经济学家JosephLouisFrancoisBertrand提出,与Cournot模型中参加博弈的双方仅以产量作为决策的变量相比,Bertrand模型中参加该博弈的双方都以价格作为决策变量。这一改变使博弈的市场均衡完全不同于Cournot均衡。它是关于双寡头产品价格竞争的一种模型,会导致每个企业的定价采用完全竞争情况下的价格,即所谓的边际成本定价法。近年来有限理性方法[1]和Puu的不完全信息法[2]也用于研究垄断市场的两个不同的框架。有限理性的企业是基于离散时间和利用边际利润的局部估计来实现其生产策略。而所谓的Puu的不完全信息法,主要优势是其现实性,因为在预测一个企业产量时,其不需要知道利润函数在当前时间步骤的具体形式,而只需知道利润和价格在过去两个时间步骤的数值。为了更好地分析垄断市场的企业竞争状况,国内外学者对此进行了多方面的研究。2008年闫安等将传统的Bertrand模型进行了修正,得到了两阶段情形下两个企业同时博弈的耐用品动态Bertrand模型[3]。2014年Ahmed等利用有限理性法和不完全信息法对Cournot模型进行分析研究[4]。
大量研究着眼于静态模型到动态模型的转化以及求解模型的均衡点,但没有针对系统出现的复杂混乱现象给出合理的控制方法。本文利用有限理性方法和Puu的不完全信息方法,将静态的Bertrand模型[5]转化为动力系统[6],对动态模型进行了数值模拟,并通过状态反馈和参数调整法对出现的混沌现象加以控制,实现了垄断市场由混乱到稳定的回归。
1模型的建立与分析
1.1 静态Bertrand模型
本文研究市场中只存在两个企业的双寡头情形(假设企业间生产的是可替代但不相同的产品),为了便于分析,可将需求函数[7]定义为
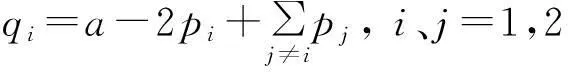
(1)
可得:
q1=a-2p1+p2,q2=a-2p2+p1。
(2)
其中,pi是企业i的产品价格,qi是企业i的产量,参数a>0,i、j=1,2,边际成本定义为线性函数:
C(qi)=c,c>0。
(3)
定义利润函数:
πi=(pi-c)qi,i=1,2。
(4)
1.2 动态Bertrand模型及分析
有限理性方法使用一个基于局部评估调整机制的边际利润[8-9],描述这个动态调整机制的动力系统如下:
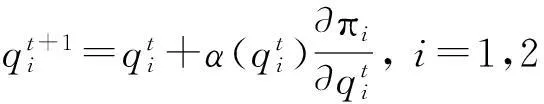
(5)
各企业的利润函数:
(6)
因此,双寡头系统可转化为如下动力系统:
(7)
系统有以下均衡点:
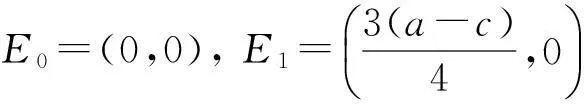
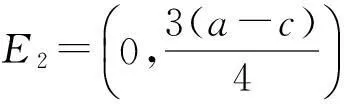
(8)
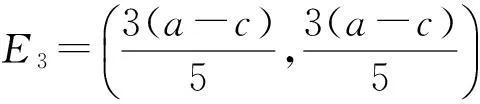
当a>c时(可保证平衡产量为正),固定点E1与E2被定义为一个垄断平衡。为得到更多关于两个垄断点的信息,进行如下分析与证明。
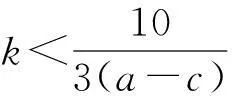
证明基于标准的特征值分析,点E0的Jacobian矩阵为

(9)
它的特征值为λ1=λ2=1+k(a-c)。显然,当a>c时,两个特征值都大于1,因此固定点E0为排斥节点。
点E1的Jacobian矩阵为
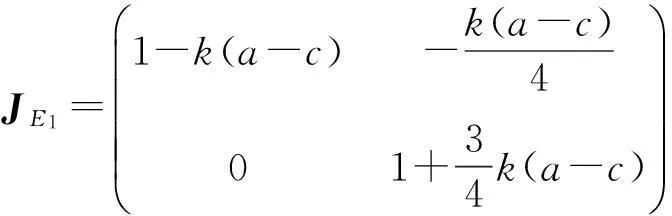
(10)
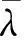
进一步研究固定点E3的稳定性,其Jacobian矩阵为
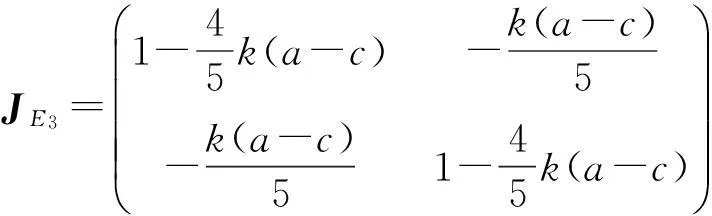
(11)
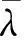
图1为企业产量随控制参数的变化图,从中可以发现,当a=4,c=0.5,k∈[0,0.9]时,变量q1、q2随着k值的变化出现分叉现象(其中横坐标代表k,纵坐标代表q1、q2)。只有当k<0.573时,系统才处于局部稳定状态。
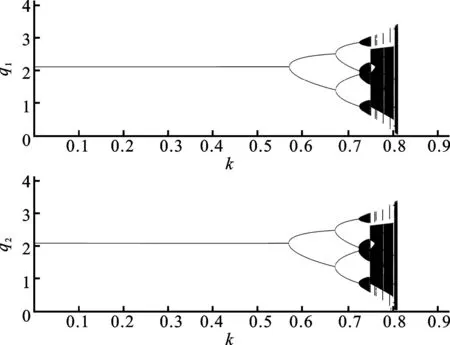
图1 变量q1、q2随k值变化的分岔图Fig.1 Bifurcation diagram for the quantities q1and q2 with respect to the adjust speed k
采用Puu的不完全信息方法来研究Bertrand模型[10-11],此方法中企业产量可以表达为

(12)
(13)
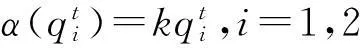
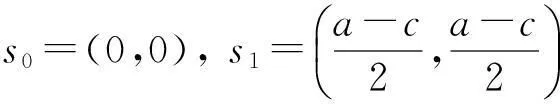
(14)
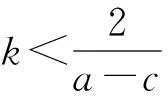
证明(ⅰ)的证明同命题1,不再赘述。为了讨论均衡点S1的局部稳定性,给出了它的Jacobian矩阵,如下:
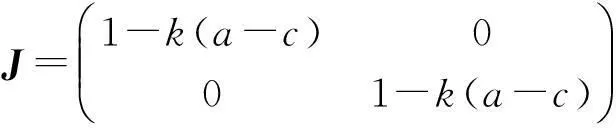
(15)
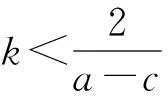
2混沌控制
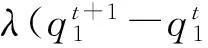
(16)
当参数a=4,c=0.5,k=0.8时,加入控制参量前的系统处于混乱状态,但是对于加入线性控制后的系统,当λ>0.42时系统是稳定的。
从图2可发现,经过控制的系统一开始处于混乱状态,但是随着控制系数λ的增加,经过一段时间后系统达到稳定。
(17)
稳定变量λ的值为0.4,此时系统出现分叉,在不同的控制方式下给定参量k不同的初值,得到不同的图像,见图2(k=0.8)和图3(k=1.42)。对比图2和图3以及参数k的取值,发现图2和图3随着参数λ的不断变化,系统均逐渐由混乱趋于稳定,不同在于图3参数k的初值比图2取值更大,即图3系统是在比图2系统更混乱的状态下趋于稳定。
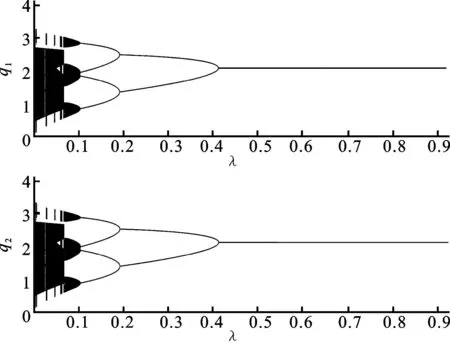
图2 线性控制下方程(16)中变量q1、q2随λ值变化的混沌控制图(k=0.8)Fig.2 Chaos control chart of the quantities q1 and q2in equation(16) with respect to the linear control factor λ
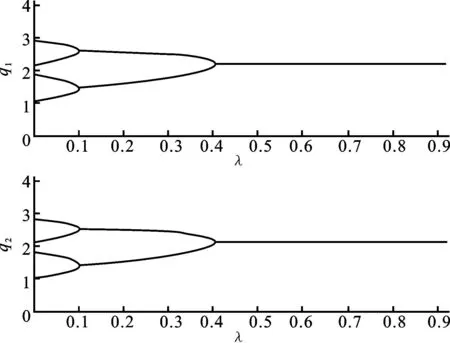
图3 非线性控制下方程(17)中变量q1、q2随λ值变化的混沌控制图(k=1.42)Fig.3 Chaos control chart of the quantities q1 and q2in equation(17) with respect to the nonlinear control factor λ
对比两种控制方法,控制参数k的给定值一样(k=0.8),发现系统的稳定状态不同,分别见图2(线性控制)和图4(非线性控制)。图2的系统随着参数λ的值不断变化,系统逐渐从混乱趋于稳定;而图4的整个系统此时都是处于稳定状态。
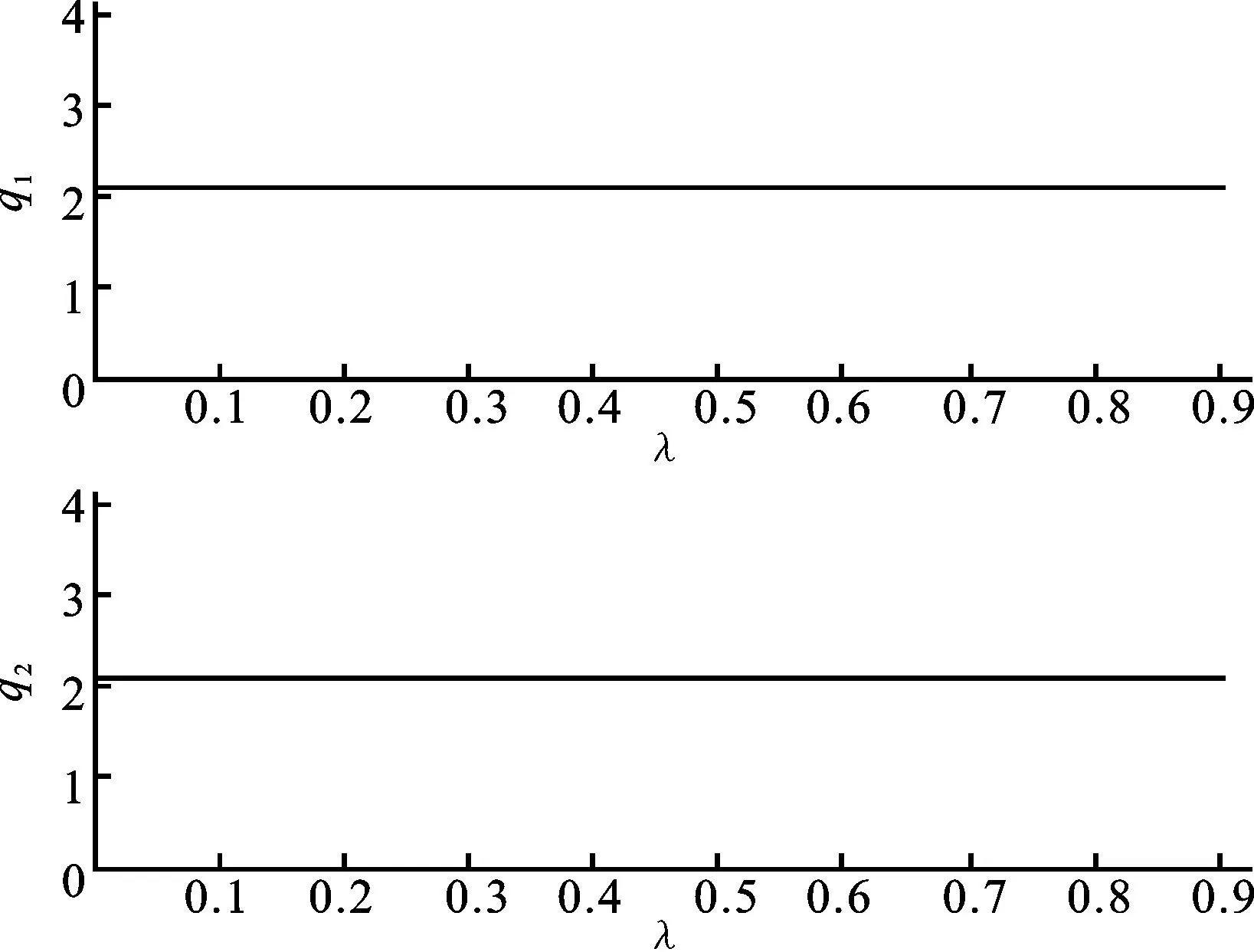
图4 非线性控制下方程(17)中变量 q1、q2随着λ值变化的混沌控制图(k=0.8)Fig.4 Chaos control chart of the quantities q1 and q2in equation(17) with respect to the nonlinear control factor λ
综合上述两种状态,认为非线性反馈控制比线性反馈控制混乱控制更加有效。
以上两种控制法是对系统的两个方程同时进行控制。针对第一种控制法,只对其中一个方程进行控制,系统将满足:
(18)
且同时满足初值k=0.8,得到图5。

图5 不对称控制下方程(18)中变量q1、q2随λ值变化的混沌控制图(k=0.8)Fig.5 Chaos control of the quantities q1 and q2 in equation(18)with respect to the asymmetric control factor λ
对比图2和图5,发现图2比图5更快地趋于稳定,即对企业双方都进行控制比只对一方进行控制能使市场更有效地趋于稳定。
3结论
本文提出了两种不同的重复Bertrand双寡头模型。基于模型中的函数和有关市场信息,企业可以通过做一些合适的计算做出合理的决策。特别地,研究了两个不同的模型,在模型中两个企业生产同质的产品,面临着具有线性成本函数的非线性需求。通过使用有限理性方法和Puu的不完全信息方法来描述这两个模型,从而使企业做出决策。在不完全信息方法下,企业通过过去两次的生产量来决定未来的生产量,而在其他方法中未来的生产量取决于随之增长的利润方向。基于这两种方法,改进了相应的离散动力系统被提升,使之包括了双寡头垄断情况。另外,本文还通过数值模拟来验证系统的稳定性,从数值模拟结果可推断迅速调整产品价格,可能会导致市场结构的混乱,同时也尝试通过状态反馈和参数调整法来稳定混乱系统,从而使产品的价格实现从混乱到稳定的发展。
参考文献:
[1]NaimzadaA,SbragiaL.Oligopolygameswithnonlineardemandandcostfunctions:twoboundedlyrationaladjustmentprocesses[J].ChaosSolitonsFractals,2006,29:707-722.
[2]AhmedE.OnPuu′sincompleteinformationformulationforthestandardandmulti-teamBertrandgame[J].Chaos,SolitonsandFractals,2006,30(5):1180-1184.
[3]闫安,达庆利,刘心报.耐用品动态Bertrand模型[J].系统工程,2008,26(5):123-126.
[4]AhmedE,ElettrebyMF.Controlsofthecomplexdynamicsofamulti-marketCournotmodel[J].EconomicModeling,2014,37:251-254.
[5]魏灿秋.博弈论模型对“价格战”现象的分析和对策建议[J].四川大学学报:自然科学版,1999,36(3):472-475.
[6]AndrewLedvina,RonnieSircar.DynamicBertrandoligopoly[J].AppliedMathematicsandOptimization,2011,63:11-44.
[7]NaimzadaA,RicchiutiG.Monopolywithlocalknowledgeofdemandfunction[J].EconomicModeling,2011,28:299-307.
[8]YuRuiwu,ZhangJiantong.DynamicpropertiesofCournot-Bertrandduopolyadvertisingmodelundernashbargaining[J].ICICExpressLetters,2013,4(6):1643-1649.
[9]AskarSameh.TheriseofcomplexphenomenainCournotduopolygamesduetodemandfunctionswithoutinflectionpoints[J].CommunicationsinNonlinearScienceandNumericalSimulation,2014,19(2):1918-1925.
[10]AhmedE,ElsadanyAA,PuuTonu.OnBertrandduopolygamewithdifferentiatedgoods[J].AppliedMathematicsandComputation,2015,251(1):169-179.
[11]WuFang,MaJunhai.Hyperchaoticdynamicofcournot-bertrandduopolygamewithmulti-productandchaoscontrol[J].WSEASTransactionsonMathematics,2014,13(1):152-160.
[12]FantiLuciano,GoriLuca.ThedynamicsofaBertrandduopolywithdifferentiatedproducts:Synchronization,intermittencyandglobaldynamics[J].Chaos,SolitonsandFractals,2013,52(1):73-86.
[13]RenWenbo,MaJunhai.ResearchonpricegameprocessandwaveletchaoscontrolofthreeoligarchsinsurancemarketinChina[J].WSEASTransactionsonSystemsandControl,2014,9(1):454-463.
〔责任编辑李博〕
第一作者:马良财,男,副教授,博士,研究方向为计算材料学。E-mail:maliangcai@126.com
ThecomplexphenomenaandthechaoscontrolofBertrandmodel
YAOHongxing1,WANGMei2
(1SchoolofEconomic;2SchoolofScience,JiangsuUniversity,Zhenjiang212013,Jiangsu,China)
Abstract:Basedonthespecificdemandfunction,aduopolyBertrandmodelisestablished.Theenterprisecompetitionphenomenoninproducinghomogeneousproductsunderthemonopolymarketisanalyzed.Thecompetitionmodelistransformedfromstaticmedeltodynamicmodelbyboundedrationalityandincompleteinformationmethod.Undersuchcondition,thepriceequilibriumsolutionofthedynamicmodelandthesteadystateofequilibriumpointsareobtained.Theregressionofmonopolymarketfromchaostostableisachievedbydifferentchaoscontrolmethods.
Keywords:Bertrandmodel;boundedrationality;incompleteinformation;bifurcation;chaos
基金项目:宁夏自然科学基金资助项目(NZ14013)
收稿日期:2014-11-05
doi:10.15983/j.cnki.jsnu.2015.02.222
文章编号:1672-4291(2015)02-0028-06
中图分类号:O211;F224.9;F270
文献标志码:A

