一类具有食饵选择的捕食-食饵模型的定性分析
李 师, 李艳玲, 杨文彬
(陕西师范大学 数学与信息科学学院, 陕西 西安 710119)
一类具有食饵选择的捕食-食饵模型的定性分析
李师,李艳玲*,杨文彬
(陕西师范大学数学与信息科学学院,陕西西安710119)
摘要:研究一类具有食饵选择的两物种间的捕食-食饵模型正平衡态解的存在性。利用上下解方法,给出系统非负平衡解的先验估计。以食饵的增长率r为分歧参数,利用局部分歧定理给出正常数解处分歧解的具体形式,并通过全局分歧理论将局部分支延拓到无穷。
关键词:捕食-食饵模型;可供选择的食饵;Holling-typeⅡ型;全局分歧
MRsubjectclassification:35K57
在生态系统中,某些种类的捕食者并不以单一的某类食饵为食,而可能随着季节的更替、种群的迁移或由于生存空间的规模远大于某类食饵的栖息地空间选择其他食饵。食饵的充裕性及可供选择的食饵的丰富性,对该类捕食者的发展都有一定的影响。因此,在研究一类较接近实际的捕食-食饵模型时,需考虑可供选择的食饵所产生的影响。近年来,对捕食者提供额外食饵补充所产生的影响及其在生态调控中的作用已成为研究热点。对捕食者有食饵补充的捕食-食饵模型已有许多研究,文献[1]说明正解的持久性主要依赖于收获力和对额外食饵的吸收,并且表明额外食饵补充对捕食-食饵模型具有重要的影响。文献[2-3]讨论了正常数解存在和稳定的条件及非常数平衡解的存在性。文献[4]研究了常微分方程模型下系统非负常数解的稳定性及全局渐近稳定的条件。本文主要考察该类捕食-食饵模型的动力学性质,对以下扩散模型进行研究:
(1)

(2)
1平衡解的局部分歧
系统(2)至多有3个非负常数解,其中平凡解(0,0)、半平凡解(k,0)恒存在。当
(3)
成立时,正常数平衡解E*=(u*,v*)存在,其中

d=A+m-1。
引理1若u(x)、v(x)是系统(2)的非负解,则

(4)
证明由于

βrk-dv+dβ(k-u)=βk(r+d)-dw。
为方便起见,令


则系统(2)在(u*,v*)处的线性化算子为

(5)
其中



g1=gv(u*,v*)=0。
由线性化理论知,若L所有特征值的实部都小于零,则解(u*,v*)渐近稳定;若L有实部大于零的特征值,则(u*,v*)不稳定。考虑特征值问题
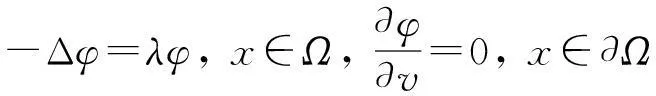
其特征值λi满足:0=λ0<λ1<λ2<…→∞,设λi的代数重数为mi,φij为对应的一组标准化特征函数,(φ,ψ)为L对应于特征值μ的特征函数,令
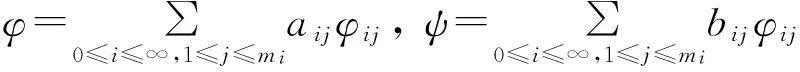

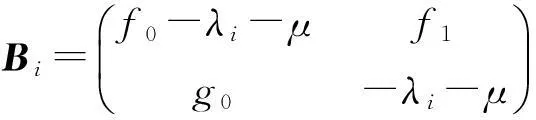
(7)
因此,L的特征值为以下特征方程的解:
μ2+Piμ+Qi=0,
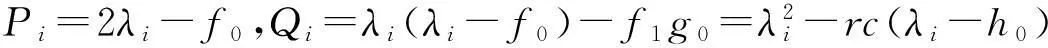

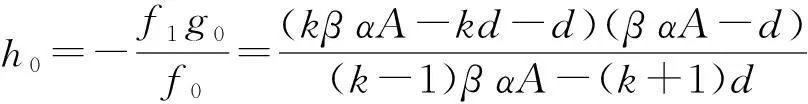

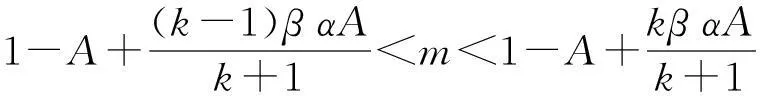
成立,因为P0<0,Q0>0,所以(u*,v*)不稳定。
类似文献[6-8]中的方法,利用局部分歧理论[9]分析一维情况下系统(1)在正常数解(u*,v*)处的非常数正平衡解的存在性。考察在区间(0,l)上的以下系统:
(8)
特征值问题
-φ″=λφ,x∈(0,l),φ′=0,
(9)
构成了空间L2(0,l)的一组标准正交基。令Y=L2(0,l)×L2(0,l),且具有内积:(U1,U2)Y=(u1,u2)L2(0,l)+(v1,v2)L2(0,l),其中U1=(u1,u2),U2=(v1,v2),并令E={(u,v):u,v∈C2([0,l]),u′=v′=0,x=0,l},以r作为分歧参数,定义映射F:(0,∞)×E→Y为

对任意的r>0,都有F(r,U*)=0,其中U*=(u*,v*)。

证明令
L0=FU(rj,U*),L1=FrU(rj,U*),
则

设(φ,ψ)∈ker(L0),并令φ=∑aiφi,ψ=∑biφi,
则有

(10)
计算可得

(11)
取r=rj时,可得
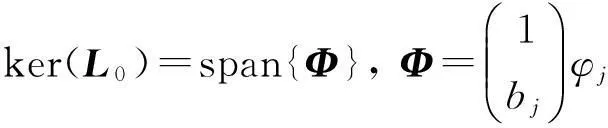
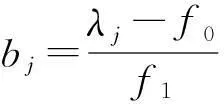

(12)
类似上面的做法可得



又因为


2局部分歧解的延拓
定理2在定理1的假设下,由(rj,(u*,v*))产生的局部分歧可以延拓成全局分歧。

(13)


并令


则(13)式可变形为

(14)

(1)证明1是K(rj)的特征值,且代数重数为1。
设(φ,ψ)∈ker(K(rj)-I),由定理1的证明过程可知
ker(K(rj)-I)=ker(L0)=span{Φ}。


其中f0、f1、g0如(6)式中定义。由于φ=∑aiφi,ψ=∑biφi,则有


ker(K*(rj)-I)=span{Φ1},



index(I-K(r)-H,(r,(0,0)))=
deg(I-K(r),B,0)=(-1)ρ,
(15)
其中B是0的邻域,ρ是K(r)所有大于1的特征值的代数重数之和[11]。依照全局分歧理论[12],需证明对充分小的ε>0,有下式成立:
index(I-K(rj-ε)-H,(rj-ε,(0,0)))≠
index(I-K(rj+ε)-H,(rj+ε,(0,0)))。
(16)
事实上,若设μ为K(r)的一个特征值,对应的特征向量为(φ,ψ),则
同样,令φ=∑aiφi,ψ=∑biφi,可得

故K(r)的特征值满足以下特征方程:
(1+λi)2μ2-(2+f0)(1+λi)μ+
1+f0-f1g0=0。
(17)

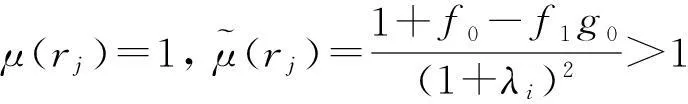

(1+λj)(2λj-f0)μ′(rj)=c(λj-h0)。
由于h0<λj<2h0,故μ′(rj)<0,即μ(r)关于r在rj邻域内单调递减,从而有
μ(rj+ε)<1,μ(rj-ε)>1。
对于充分小的ε>0,K(rj-ε)大于1的特征值比K(rj+ε)多一个,类似于前面的证明,可知μ(rj-ε)的代数重数为1,因此(16)式得证。综合(1)、(2)和全局分歧定理可知,由(rj,(u*,v*))产生的局部分歧可以延拓成全局分歧Γj,使得下面两种情况中的一种成立:
(ⅰ)Γj连接(rj,U*)到(rk,U*),其中k≠j;
(ⅱ)在R×E中,Γj连接(rj,U*)到∞。
定理3在定理1假设下,Γj连接(rj,U*)到∞。
证明利用反证法。假设Γj连接(rj,U*)到(rk,U*),k≠j,并且对任意的i>k,Γj不经过(ri,U*)。现考虑如下系统:
(18)

(19)


3数值模拟
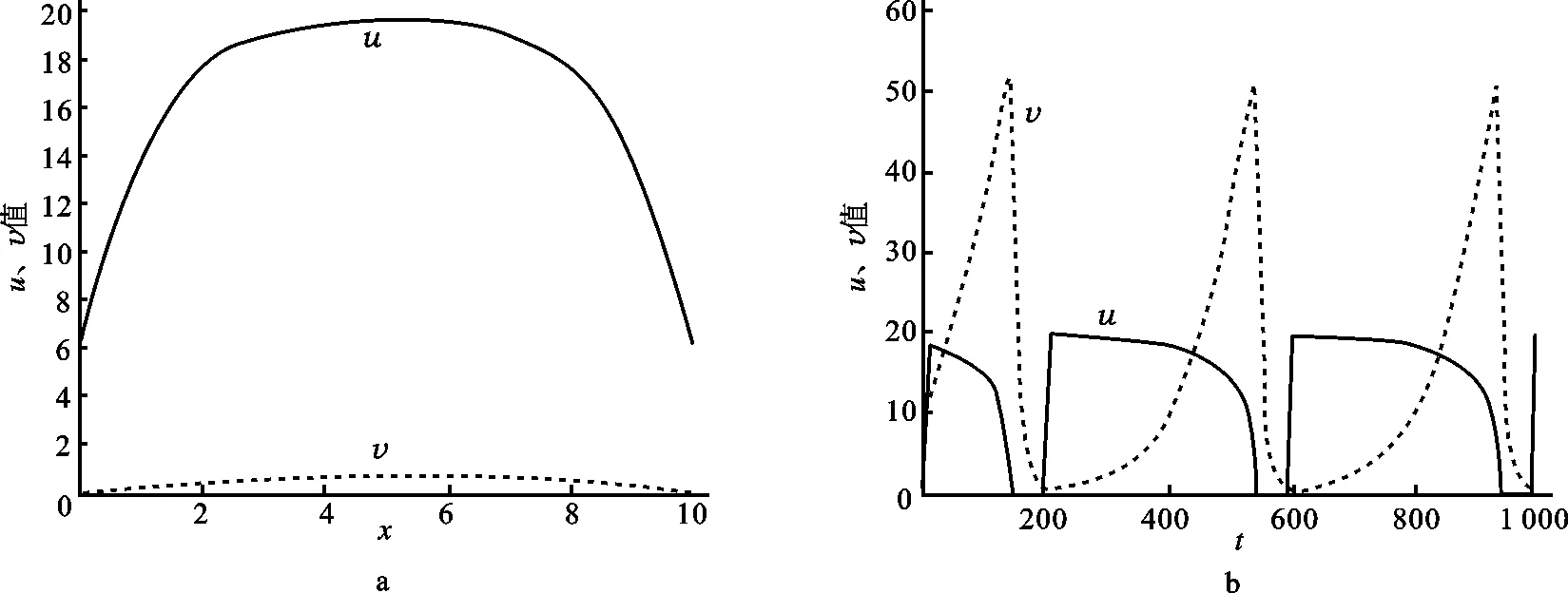
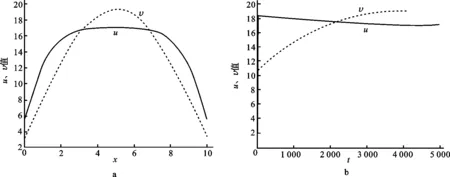
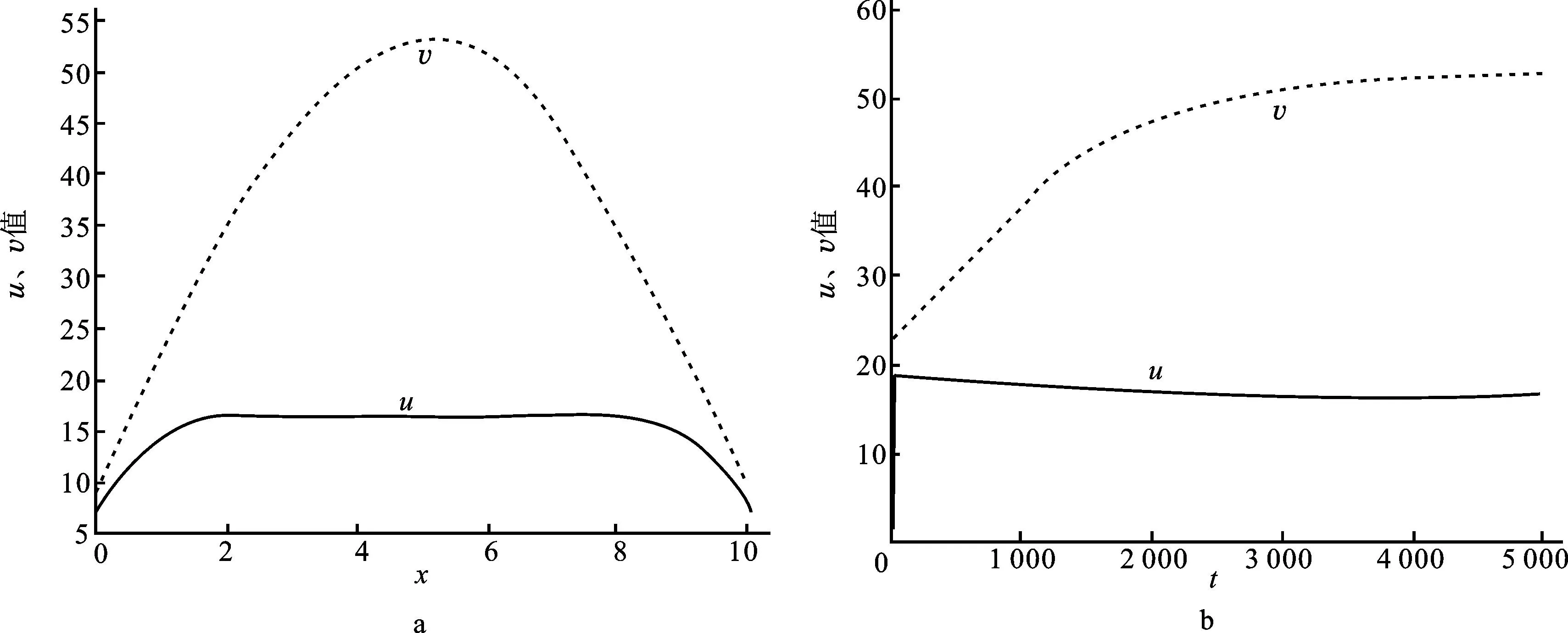
下面给出系统(1)的数值模拟图像(如图1—6所示),给定一组参数值:k=20,α=0.16,β=0.8和m=0.2,它们在数值模拟过程中保持不变。通过改变参数r、A的值(0 图1 A=0.805时,系统(1)的数值解关于x和t的变化Fig.1 The numerical solution of the system (1) changes with the change of x and t其中r=1,k=20,α=0.16, β=0.8和m=0.2。 图2 A=0.82时,系统(1)的数值解关于x和t的变化Fig.2 The numerical solution of the system (1) changes with the change of x and t其中r=1。其他参数为:k=20,α=0.16,β=0.8和m=0.2。 图3 A=0.85时,系统(1)的数值解关于x和t的变化Fig.3 The numerical solution of the system (1) changes with the change of x and t其中r=1。其他参数为:k=20,α=0.16,β=0.8和m=0.2。 图5 A=0.82时,系统(1)的数值解关于x和t的变化Fig.5 The numerical solution of the system (1) changes with the change of x and t其中r=2。其他参数为:k=20,α=0.16,β=0.8和m=0.2。 图6 A=0.85时,系统(1)的数值解关于x和t的变化Fig.6 The numerical solution of the system (1) changes with the change of x and t其中r=2。其他参数为:k=20,α=0.16,β=0.8和m=0.2。 4结语 本文提出了一类Neumann边界条件下具有食饵补充的捕食-食饵扩散模型。通过比较原理给出了非负解的先验估计,利用经典的Rabinowitz分歧定理讨论了非常数正解的存在性,得到局部分歧解存在的充分条件,并将其沿分歧参数r延拓到无穷。结果表明:当食饵补充参数A控制在一定范围时,只要食饵增长率充分大,食饵与捕食者便可共存(即非常数正解存在)。 参考文献: [1]KarTK,ChattopadhyaySK.Afocusonlong-runsustainabilityofaharvestedpreypredatorsysteminthepresenceofalternativeprey[J].ComptesRendusBiologies,2010,333(11):841-849. [2]NarayanKL,RamacharyuluNCP.Aprey-predatormodelwithanalternativefoodforthepredator,harvestingofboththespeciesandwithagestationperiodforinteraction[J].InternationalJournalofOpenProblemsComputerScienceandMathematics,2008,1(1):71-79. [3]ReddyKM,NarayanKL.Aprey-predatormodelwithanalternativefoodforthepredatorandoptimalharvestingoftheprey[J].AdvancesinAppliedScienceResearch,2011,2(4):451-459. [4]KarTK,GhoshB.Sustainabilityandoptimalcontrolofanexploitedpreypredatorsystemthroughprovisionofalternativefoodtopredator[J].Biosystems,2012,109(2):220-232. [5]叶其孝,李正元.反应扩散方程引论[M].北京:科学出版社,1990:37-39. [6]王利娟,李艳玲.Oregonator模型的平衡态正解分析[J].陕西师范大学学报:自然科学版,2012,40(3):6-11. [7]姚若飞,李艳玲.具有阶段结构的捕食-食饵模型的定性分析[J].陕西师范大学学报:自然科学版,2013,41(1):10-14. [8]杨文彬,李艳玲.一类异构捕食-食饵退化模型正解的存在性[J].陕西师范大学学报:自然科学版,2015,43(1):13-18. [9]JaeduckJ,NiWeiming,TangMoxun.Globalbifurcationandstructureofturingpatternsinthe1-DLengyel-Epsteinmodel[J].JournalofDynamicalDifferentialEquations,2004,16(2):297-320. [10]SmollerJ.Shockwavesandreactiondiffusionequations[M].NewYork:Springer-Verlag,1999. [11]钟承奎.非线性泛函分析引论[M].兰州:兰州大学出版社,2004:104-105. [12]WuJianhua.Globalbifurcationofcoexistencestateforthecompetitionmodelinthechemostat[J].NonlinearAnnalsSerialA:TheoryMethods,2000,39(7):817-835. 〔责任编辑宋轶文〕 第一作者:王洪峰,男,讲师,主要研究方向为分布式并行计算与智能优化算法。E-mail:40577025@qq.com Qualitativeanalysisofapredator-preymodelwithalternativeprey LIShi,LIYanling*,YANGWenbin (SchoolofMathematicsandInformationScience,ShaanxiNormalUniversity, Xi′an710119,Shaanxi,China) Abstract:Theexistenceofpositivesteady-statesolutionsofatwospeciespredator-preymodel,inwhichthepredatorispartiallycoupledwithalternativepreyisinvestigated.Bymeansofloweranduppersolutions,aprioriestimateofthenon-negativesteady-statesolutionsofthesystemisgiven.Takingtheintrinsicgrowthrateofthepreypopulationrasabifurcationparameter,theconcreteformofsolutionsbifurcatedfromthepositiveconstantsolutionisgivenbylocalbifurcationtheoryandthelocalbifurcationsolutionscanalsobeextendedtoinfinitebyusingglobalbifurcationtheory. Keywords:predator-preymodel;alternativeprey;Holling-typeⅡ;globalbifurcation 基金项目:国家自然科学基金资助项目(61103143,70890081);中国博士后科学基金资助项目(2012M512008);河南省科技厅科技发展计划基础与前沿技术研究项目(142300410402);河南省教育厅高校创新人才支持计划项目(2012HASTIT032);河南省教育厅科学技术研究重点项目指导计划基础前沿项目(14B520057) 收稿日期:2014-10-08 doi:10.15983/j.cnki.jsnu.2015.02.123 文章编号:1672-4291(2015)02-0015-09 中图分类号:O175.26 文献标志码:A