基于Shapley值的中国电力需求组合预测模型



基于Shapley值的中国电力需求组合预测模型

严国津

(上海电力学院 经济与管理学院, 上海200090)

电力工业是为国民经济和社会进步提供能源的基础工业,对于提高人民物质生活水平有着重要的保障作用.近年来,我国对于电力这种清洁二次能源的需求量越来越大,确保用电量的准确预测以及充足稳定的供应,将很大程度决定着国家的经济发展水平和社会的进步程度.因此,科学运用预测模型来精确分析中国未来的电力需求状况,具有十分重要的现实意义.

随着国内外学者对预测方法的积极探索,从各学科出发,至今已出现了许多实用的预测方法,如回归分析法、系统动力学法、支持向量机法[1]、神经网络法[2]、小波回归分析法[3]、灰色预测法[4-5]等.从现有文献来看,多数预测采用的是单一预测法,难以有效利用各种有效信息,从而导致预测精度不高,而通过权重系数的分配构建组合模型更能实现科学预测.一般来说,电力消费时间序列都是非平稳的,依靠差分的方法可将其转换为平稳序列,而对于平稳时间序列,则可采用计量经济学中十分成熟的自回归积分滑动平均模型(Autoregressive Integrate Moving Average Model,ARIMA模型)进行建模分析;3次指数平滑法配合的是一条二次曲线,其计算过程相对简单且适应性较强.基于此,本文将3次指数平滑法和ARIMA模型进行组合,并应用Shapley值法[6]来确定两者所占权重,再通过实例验证该方法的有效性.

1ARIMA模型

ARIMA模型是由统计学家博克思和詹金斯于20世纪70年代初提出的,又称为博克思-詹金斯模型,简称B-J模型.建立ARIMA(p,d,q)模型的步骤如下[7]:

(1) 序列的平稳性检验先判断该时间序列是否为平稳序列,若非平稳,则需要经过差分处理来满足建模要求;

(2) 对模型的识别根据所得时间序列的自相关图和偏自相关图,分析选定适当的p值和q值;

(3) 对模型的参数估计及检验依据时间序列数据,按照基本识别规则建立模型,并分析其中的各种参数,选出最优的模型;

(4) 预测利用选出的ARIMA模型进行动态与静态预测.

1.1　序列的平稳性检验

本文基于1997~2013年中国的年用电量,建立ARIMA模型并进行分析,利用Eviews 8.0软件进行数据处理(文中所用数据来自中经网统计数据库).图1为1997~2013年中国的电力消费趋势示意.

图1　中国电力消费趋势示意

将电力消费原序列记为EC,由图1可以看出,原序列不平稳.为消除序列的异方差性,对原序列作对数处理,用字母L表示.序列LEC经各阶差分后的单位根检验结果如表1和表2所示.

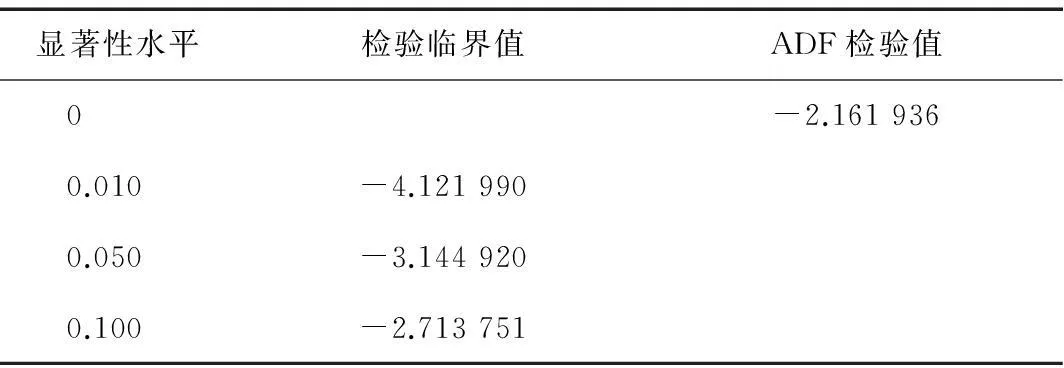
表1　序列LEC经一阶差分后单位根检验结果

表2　序列LEC经二阶差分后单位根检验结果

对LEC作一阶差分并进行ADF检验.由表2可以看出,检验t统计量的值大于10%的临界值,序列仍存在单位根,为非平稳序列;而表3中LEC作二阶差分后检验t统计量的值小于1%的临界值,二阶差分后得到的序列是平稳的.

1.2　ARIMA模型的识别

序列LEC经二阶差分后,其初始定阶可通过观察自相关函数与偏自相关函数显著不为零的滞后阶数来选定.图2为序列LEC经二阶差分后自相关和偏相关示意.由图2可以看到,自相关系数(AC)在滞后期k=2或k=5后快速趋于零;偏自相关系数(PAC)在滞后期k=2后快速趋于零.因此,初步建立ARIMA(2,2,2),ARIMA(2,2,3),ARIMA(2,2,4),ARIMA(2,2,5)4个模型.

1.3　ARIMA模型的参数估计及检验

通过检验特征根发现,ARIMA(2,2,5)的特征根绝对值中含有大于1的值,不满足可逆性条件,可将其剔除.而对比分析其余3组ARIMA模型的AIC值、SC值与可决系数,发现ARIMA(2,2,3)的AIC值和SC值均为最小,同时可决系数值为最大,故认为ARIMA(2,2,3)模型更为合适.采用最小二乘法对ARIMA(2,2,3)模型的参数进行估计,结果如表3所示.

表3　ARIMA(2,2,3)模型参数估计结果

对ARIMA(2,2,3)模型的残差进行Q-检验,发现其为白噪声过程.因此,可确定ARIMA(2,2,3)模型为最优模型.

1.4　ARIMA模型预测

利用上述过程选定的ARIMA(2,2,3)模型对数据进行拟合预测(静态预测).

23次指数平滑模型

2.1　指数平滑模型的建模

设时间序列为X1,X2,X3,…,Xt,指数平滑值记作S,第t期的1次、2次、3次指数平滑值分别记为St(1),St(2),St(3),对应计算公式为:

(1)

(2)

(3)

式中:Xt——第t期的实际值;

3次指数平滑法的数学公式为:

(4)

(5)

(6)

(7)

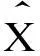
at,bt,ct——平滑系数.

在进行平滑计算前应确定初始值的大小.实际计算中一般都会采用如下方式进行处理:当原始序列项数较少时(如小于20项),初始值会对最后结果产生一定影响,可选用最初几期观测值的平均值来代替;而当序列项数较多时(如大于20项),初始值可由首期观测值直接代替.

2.2　指数平滑模型的预测

本文取α=0.45,用前3期的平均值作为初始值,以2013年为基年,计算出at,bt,ct系数值分别为at= 54 218.29,bt= 4 267.66,ct=79.68,由此可建立数学模型为:

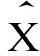
(8)

根据式(8),当T = 2时,预测值即为2015年的电力需求量.

3组合预测模型

构造线性组合模型主要在于判定各模型所占权重系数,本文采用合作对策理论中的Shapley值法来求解权重.

3.1　Shapley值法确定权重

Shapley值法是一种用于解决多人合作对策问题的数学方法.进行组合预测时,各单一预测方法对总误差的产生均有贡献,因此可将各方法之间视为一种相互合作的关系,而预测的总误差可被当作合作总收益,通过将其进行分配来确定各单一方法在组合预测模型中所占权重.

设第i种方法求得的绝对误差平均值为Ei,各单一方法在组合后的预测误差总值为:

(9)

式中:i——预测方法个数,i= 1,2,3,…,m.

基于Shapley值的分配模型公式为:

[E(s)-E(s-{i})]

(10)

式中:Ei——各模型的误差量(Shapley值);

i——第i个预测模型;

s——包括模型i的集合;

m——组合预测方法个数;

s-{i}——从组合中除去成员i;

E(s)——合作完成满足s个参与预测方法要求所要达到的误差量;

E(s-{i})——去掉第i个参与者合作完成满足s-1个参与预测方法所要达到的误差量.

单一方法在组合模型中的权重计算公式为:

(11)

式中:i——预测方法个数,i= 1,2,3,… ,m.

3.2　组合预测

根据式(9)和表2数据,可求得组合预测应分摊的总误差值为:E=(941.15+477.21)/2=709.18.其所有子集的组合误差分别为E({1}),E({2}),E({1,2}),其值分别为941.15,477.21,709.18.

根据式(10),可求得3次指数平滑模型应分摊的误差量为:

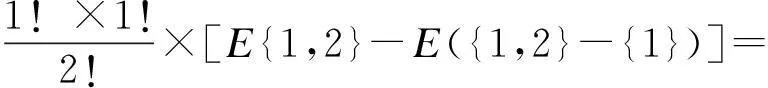
同理,可以得到ARIMA模型E2= 122.62.其中,预测模型的精度与误差分摊值呈现反向关系.

最后根据式(11),求得两种单一模型在组合中所占权重分别为:

从而构造组合模型的计算公式为:

Y=0.173y1+0.827y2

(12)

式中:Y——组合模型预测值;

y1——3次指数平滑模型预测值;

y2——ARIMA模型预测值.

根据式(12)的组合模型计算公式,对中国历年电力消费量进行数据拟合.各模型拟合结果及误差如表4所示.

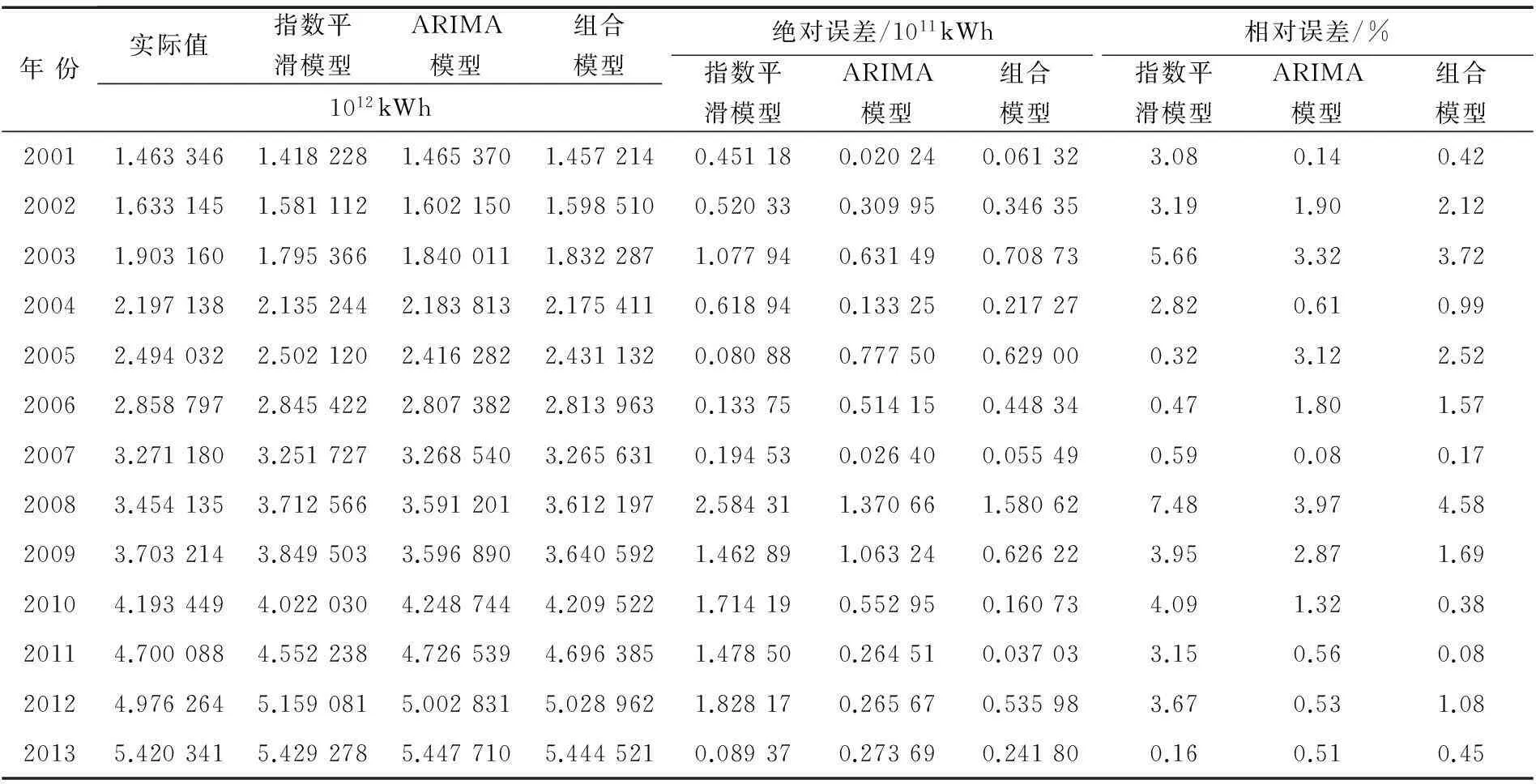
表4　模型拟合结果及误差

由表5可知,指数平滑模型、ARIMA模型、组合模型的相对误差均值分别为2.97%,1.59%,1.52%.其中,基于Shapley值法的组合模型求得的相对误差均值低于两种单一模型,所得精度比较满意.考虑到ARIMA模型在进行趋势外推时预测时间不宜过长,本文取2016年,采用动态预测.基于组合模型的2015年和2016年中国电力需求量预测结果分别为6.618 252×1012kWh,7.229 493×1012kWh.

4结语

本文选用3次指数平滑模型和ARIMA模型对中国历年电力消费量进行拟合分析,并通过Shapley值法来构造组合模型.实例结果表明,组合模型的相对误差均值仅为1.52%,小于两种单一方法所得结果,拟合精度较为理想.根据外推预测结果可知,到2016年中国的电力需求量将达到7.229 493×1012kWh,这表明政府需要做好电力发展规划及基础建设工作,确保中国电力的安全有效供应的同时,全社会还应进一步加大风能、太阳能等清洁能源的使用,以实现中国经济的可持续发展.

参考文献：

[1]杨延西,刘丁.基于小波变换和最小二乘支持向量机的短期电力负荷预测[J].电网技术,2005,29(13):60-64.

[ 2 ]赵菁,许克明.神经网络和模糊理论在短期负荷预测中的应用[J].电力系统及其自动化学报,2010,22(3):129-133.

[ 3 ]张涛,朱建良.小波回归分析法在短期电力系统负荷预测中的应用[J].哈尔滨理工大学学报,2008,13(1):74-76.

[ 4 ]牛东晓,李春祥,孟明.基于灰色和偏最小二乘方法的年度负荷预测[J].华东电力,2009,37(6):989-992.

[ 5 ]张大海,毕研秋,毕研霞,等.基于串联灰色神经网络的电力负荷预测方法[J].系统工程理论与实践,2004,24(12):128-132.

[ 6 ]黄宜,赵光洲,王艳伟,等.基于Shapley值的中国能源消费组合预测模型研究[J].能源工程,2012(6):5-9.

[ 7 ]王莉琳,张维,赖敏,等.基于ARIMA-GM组合模型的湖北省电力需求预测研究[J].中国农村水利水电,2013(4):101-105.

[ 8 ]王洪德,曹英浩.道路交通事故的三次指数平滑预测法[J].辽宁工程技术大学学报:自然科学版,2014,33(1):42-46.

[ 9 ]郭金,曹福成,杨尚东,等.基于Shapley值的组合预测方法[J].华东电力,2005,33(2):7-10.

(编辑胡小萍)

摘要:针对中国1997~2013年的电力消费量,采用3次指数平滑模型和ARIMA模型分别进行了建模与拟合分析,通过合作对策理论中的Shapley值法求解了两模型所占权重,从而构建了所需组合模型,并用该组合模型预测了2015年和2016年的中国电力需求量.实例结果表明,组合模型有着更高的拟合精度,拟合相对误差平均值仅为1.52%.

关键词：三次指数平滑模型; ARIMA模型; Shapley值; 电力消费; 组合预测

Research on Combined Forecasting Model of Electric Power Demand of China Based on Shapley ValueYAN Guojin

(School of Economics and Management, Shanghai University of Electric Power, Shanghai200090, China)

Abstract:By using the electric power consumption data from 1997 to 2013 of China,cubic exponential smoothing model and ARIMA model are adopted respectively for modeling and fitting analysis.Then the weights to each single forecasting model are allocated by using Shapley value method,and the combined forecasting model is constructed.The results show that the combined model has higher fitting precision,and the average value of relative error is only 1.52%.Finally,by using the combined model,the electric power demand of China from 2015 to 2016 is predicted.

Key words:cubic exponential smoothing model; ARIMA model; Shapley value; electric power demand; combined forecasting

中图分类号：TM714; F224; F426.61

文献标志码：A

文章编号：1006-4729(2015)06-0592-05

通讯作者简介：严国津(1989-),男,在读硕士,湖北咸宁人.主要研究方向为电力能源需求预测.E-mail:yanjin680113@163.com.

收稿日期：2015-07-03

DOI：10.3969/j.issn.1006-4729.2015.06.020