油浸式变压器绕组温度场的数值计算与分析

周建聪, 龙　辉, 胡桃涛, 李　忠, 张晓群, 陈　炯, 薛　飞

(1.国网四川省电力公司 资阳供电公司, 四川 资阳　641300;

2.上海电力学院 电气工程学院, 上海　200090)



油浸式变压器绕组温度场的数值计算与分析

周建聪1, 龙辉1, 胡桃涛1, 李忠1, 张晓群1, 陈炯2, 薛飞2

(1.国网四川省电力公司 资阳供电公司, 四川 资阳641300;

2.上海电力学院 电气工程学院, 上海200090)

摘要:综合考虑了变压器油物性参数随温度的变化和变压器辐射散热的边界条件,采用ANSYS软件对一台630 kW/10 kV自然油循环油浸式变压器的温度场进行了仿真分析.仿真结果表明:随着负载的增加,绕组温度急剧上升,且热点位置基本处于绕组相对垂直高度的85%左右.

关键词：油浸式变压器; 热点温度; 数值计算

变压器的热性能是检验变压器运行状况是否良好的重要指标,国内外的生产厂家和运行部门大都把确定变压器内部温度分布,特别是变压器绕组热点温度作为重要问题,并加以研究.本文通过数值计算方法对变压器绕组的温度场进行分析与计算,在获得热点温度的同时进而对绕组热点进行精确定位,这可以直观地了解变压器内部温度场的分布以及热点发热的情况,为改善变压器内部的散热提供依据.

1建模与仿真

1.1　物理模型的建立

本文对一台630 kW/10 kV油浸式变压器建立有限元分析模型,由于变压器结构高度对称,对计算模型作如下简化假设:

(1) 模型以铁心中心为对称面,高低压绕组高度不相等,绕组采用饼式绕组形式,各线饼之间分布均匀;

(2) 绕组沿圆周径向不存在温度梯度的变化;

(3) 不考虑油箱内部结构件的影响,即在模型中不体现结构件;

(4) 考虑散热片对油路循环的影响.假设散热器的自然油循环变压器结构几何模型如图1所示.[1]

图1　自然油循环变压器二维结构模型

1.2　网格的划分

变压器流固耦合模型网格划分采用Gambit软件进行分区划分,先对固体区域进行划分,网格划分间距为2 mm,在对流体场进行划分时,若网格尺寸过大,则在油道内部计算过程会出现迭代不收敛的情况,而网格尺寸过小,则会导致计算机资源开销太大,计算效率大幅下降,因此在对铁心绕组进行结构性网格划分的同时,对垂直油道和水平油道采用局部网格加密,其余液体部分采用自由网格划分法,最后所得网格数大约为30万.[2]

1.3　控制方程的计算

变压器运行时单位时间内绕组、铁心的损耗功率不变,到达稳态时,热量的产生和散失达到平衡,变压器内部各处的温度以及各处的油流速度不随时间改变,同时外界的环境条件也保持不变.

变压器内部固体之间的导热满足傅立叶定律的热传导方程,即:

(1)

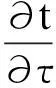
c——比热容;

ρ——密度;

qr——导体单位体积内的单位时间热生量,w/m3;

α——热扩散率.

固体与液体之间的对流换热则满足牛顿冷却公式,即:

(2)

式中:q——热流量;

h——固液接触面的对流换热系数;

tw——固体温度;

tf——流体温度.

在油流与油箱壁之间,流体温度高于固体温度,固体被加热,则公式又表述为:

(3)

油箱壁面与空气之间满足对流散热及玻尔兹曼辐射散热条件,即:

(4)

式中:ε——实际物体的辐射率,或称为黑度,其数值处于0~1之间;

σ——斯蒂芬-玻尔兹曼常数,约为5.67×10-8W/(m2·K4);

A1——辐射面1的面积;

F12——两个辐射交换面之间的形状系数;

T1——辐射面1的绝对温度;

T2——辐射面2的绝对温度.

变压器内部的油流控制方程为质量守恒方程,即:

(5)

式中:vx,vy,vz——x,y,z方向上的速度分量.

动量守恒方程为:

(6)

(7)

(8)

式中:Tx,Ty,Tz——粘性损失项;

μ——动力粘度.

能量守恒定律是根据热力学第一定律转变而来的流动系统的基本定律,对于不可压缩流体,忽略其中的粘性功、压力功、粘性耗散和动能,则其表达形式为:

(9)

式中:Cp——比热容;

T——温度;

K——导热系数;

Qv——体积热源.

在多种解决流动问题的模型中,工程中使用最多的是双方程k-ε模型,其在数学方程和求解精度之间可找到一个最佳的平衡点.k-ε中的k为湍动能,定义为速度波动的变化量,其单位为m2/s2;ε为湍动能耗散,指速度波动耗散的速率,其单位为单位时间的湍动能m2/s3.标准的k-ε湍流模型的湍流动能方程为:

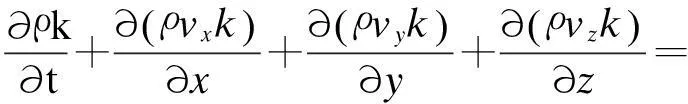
(10)

式中:σk——湍流动能方程中的施密特数;

σt——能量方程中的施密特数;

μt——湍流粘度;

g(x,y,z,t)——热流密度函数;

Φ——固体表面形状系数;

C4——湍流动能方程常数.

1.4　材料物理性质及边界条件的设定

变压器内部固体的物性参数如表1所示.[3]

对自然油循环的对流问题,ANSYS软件中的FLUENT模块有两种处理方法:一是Boussinesq近似法,二是定义密度法.在密度变化不大的自然对流问题中,Boussinesq近似法比定义密度法收敛性更好,但考虑到计算精度问题,本文选择了定义密度法,即与油的其余物性一样,把油的密度关于温度的变化采用拟合公式输入,油的物性参数随温度变化的拟合公式如表2所示.

表1　固体材料属性

表2　变压器油物性参数的拟合输入公式

注:Toil—油温.

在对本文特定模型进行计算时,需设定相应的边界条件.这里设置铁心中轴为对称条件,铁心及变压器与变压器油接触的面采用单向散热流固耦合边界条件,环境参考温度为298 K.[4]

(1) 壁面边界条件油箱壁与散热器壁的厚度可忽略不计,油箱壁与散热器壁的导热系数设定为47 W/(m·K),两者对于空气同时存在对流散热和辐射散热,其中油箱壁的对流换热系数为5 W/m2,设定辐射表面发射率与散热器相同,散热器的对流换热系数为20 W/m2.

(2) 散热器油道出入口条件自然油循环变压器中的油流循环是在油箱和散热器之间的封闭路径中,热油受热则膨胀密度减小而产生的浮力以及冷油受重力作用下沉形成了油循环的驱动力,因此油道入口和出口不另设边界条件,只设定为自由无压力条件,同时给变压器油设定初始温度为环境参考温度298 K.

(3) 热源条件变压器不同负载运行情况下,铁心的损耗基本保持不变,产热量与体积的比值为单位体积内产生的热量,即损耗发热密度.这里设定铁心损耗密度约为1 000 W/m3.额定负载条件下,低压绕组和高压绕组的直流电阻损耗分别为64 103 W/m3和18 161 W/m3,不同负载条件下绕组的直流电阻损耗与负载系数的平方成正比,绕组涡流损耗基本保持不变.

2数值计算结果与分析

对负载系数k=0.8时的自然油循环变压器温度场和油流场进行了计算,并用后处理程序得到了热点的位置,对结果进行分析.计算得到的变压器温度场云图、油流速度云图以及油流矢量图分别如图2,图3,图4所示.[5]

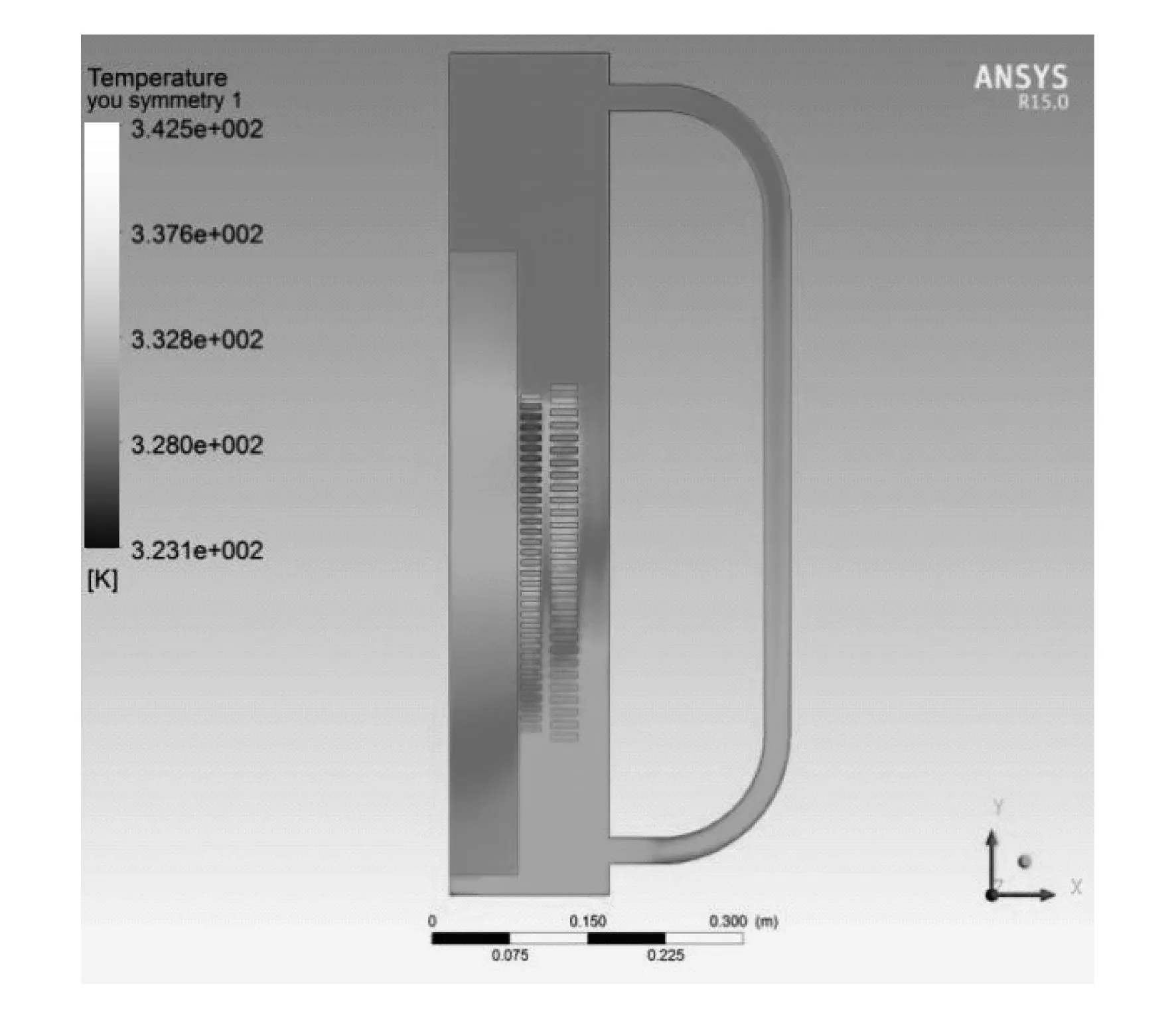
图2　k=0.8时的温度场分布

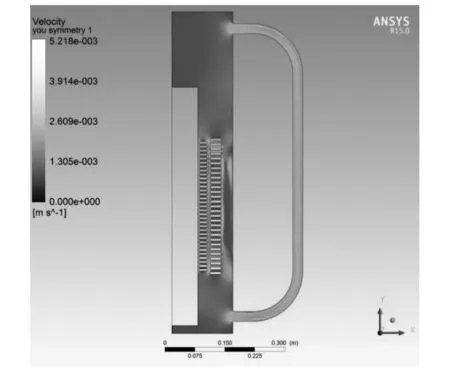
图3　k=0.8时的油流速度分布

图4　k=0.8时的油流矢量

由图4可以看出,低压绕组温度最高,高压绕组和低压绕组的上部温度明显高于下部,即纵向来看,温度从低到高基本呈逐渐增加的态势.铁心温度则是两头低中间高,散热器和油箱中的油温也是纵向从低到高温度逐渐增加,顶部油温甚至高于铁心温度.[6]为获得热点的位置,对结果进行进一步后处理,导出低压绕组和高压绕组的纵向温度分布曲线,如图5所示.

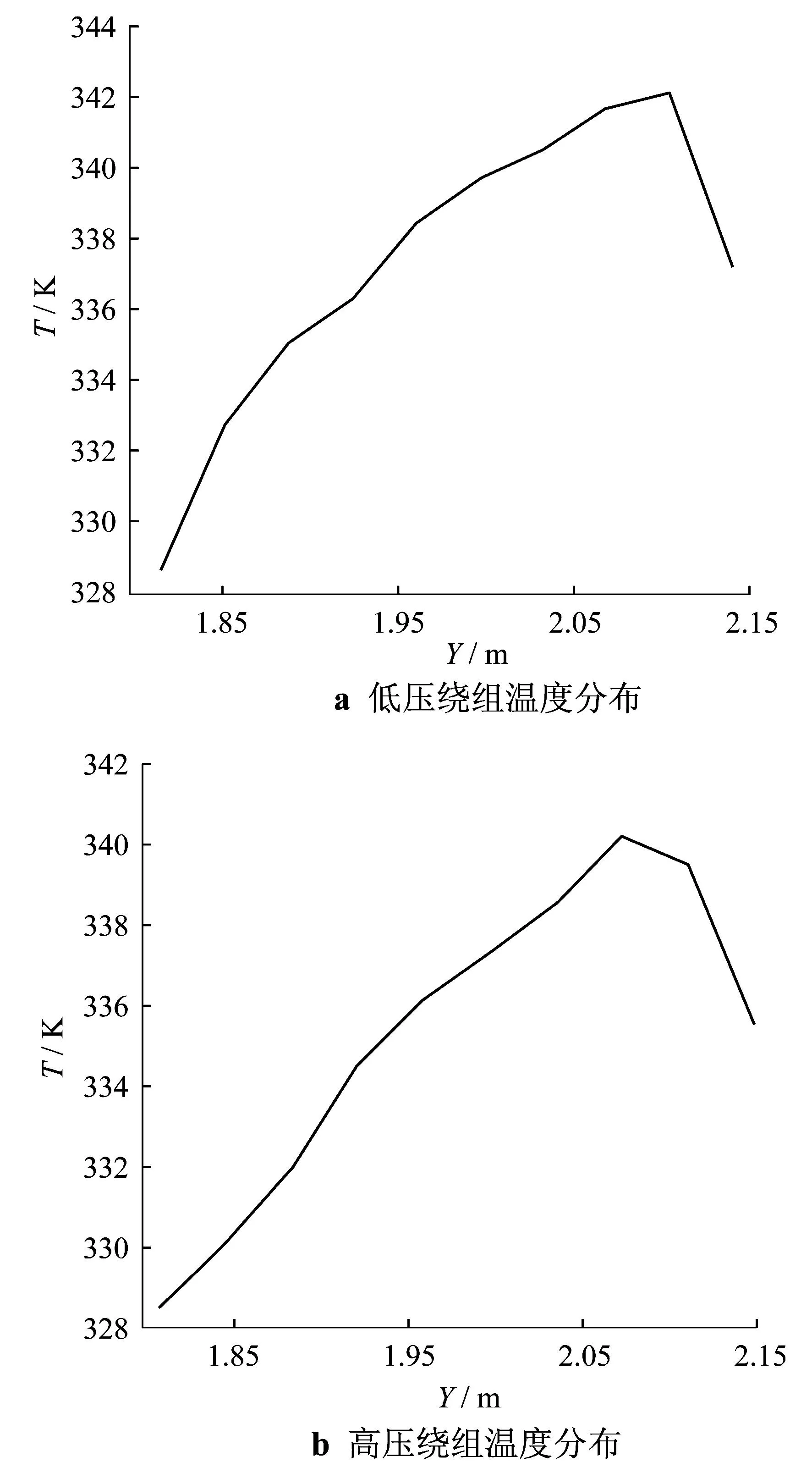
图5　k=0.8时绕组纵向温度分布曲线

由图5可知,热点出现在低压绕组纵向高度的87%的位置,温度值为342 K,同时高压绕组的最高温度也出现在低压绕组热点对应的水平位置附近,最高温度为340.3 K.靠近热源处的油流流速明显较快,表明这些地方的对流散热较为剧烈.油箱其余处的油流分布较均匀,散热器中的油流流速要大于油箱内的流速,这是因为散热器中油流对流强度要大于油箱壁附近的油流对流强度,油流流速的最大值出现在高低压绕组中间垂直油道靠近热点的地方,其值远大于其他地方的油流流速,对流强度最为剧烈,而热点处低压绕组水平油道内的油流流动却非常缓慢且水平分量几乎为零,对比热点的位置发现此处两侧同时存在大的热源,且从油道底部受热后的油向上流动在此汇聚,因此该处的散热状况最差.[7]

在此基础上,本文对变压器过载运行条件下不同负载情况的热点温度进行了计算分析,得到热点的温度值和热点位置的分布变化,如表3所示.

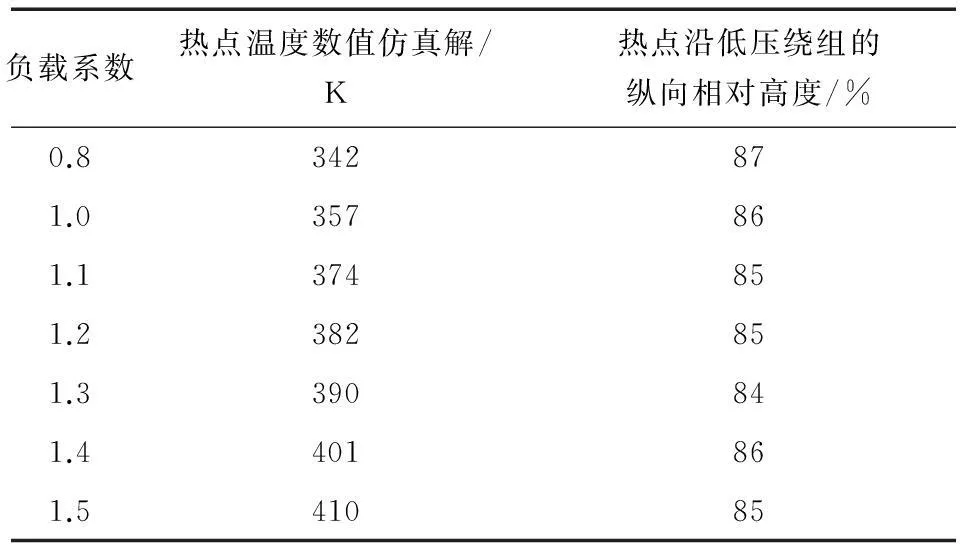
表3　负载系数对变压器热点温度的影响

由表3可以看出,当变压器过载时,绕组的产热量加大,变压器内部的散热情况变得更加恶劣,变压器要在更高的温度上才能维持产热与散热的平衡,当K=1.5时,热点温度已经远远超过负载导则所规定的长期运行的最高温度378.15 K(105 ℃),已经接近所规定的短时周期性超载运行下的最高温度413.15 K(140 ℃),根据变压器内部绝缘材料相对老化率准则,此时变压器运行1 h相当于基准值371.15 K(98 ℃)下运行128 h所产生的绝缘损耗,这将严重影响变压器的寿命,甚至直接威胁其安全运行.因此,必须密切关注变压器过载运行时热点的温度,对其进行实时监测,同时还需改善变压器的冷却条件,以免温度过高发生故障.

3结论

(1) 数值仿真计算发现:不同负载条件下绕组的热点位置基本不变,为低压绕组相对垂直高度的85%左右,同时该水平位置也基本是高压绕组的热点.仿真分析也发现,热点位置处水平油道内油流较慢,称之为“死油区”,严重影响散热,可以在热点处的垂直油道设置绝缘导油板,使得垂直油道内流速较快的油流进入水平油道内带动该处的热油循环,从而改善热点处的散热条件.

(2) 负载系数增加,绕组温度急剧上升的同时,变压器油温也相应升高,尤其各处热油都汇聚到油箱顶部后使得顶部油温最高,过高的油温不利于绕组的散热,同时还将大大降低油的绝缘性能,因此可以增加散热片的数量以及增加散热器的散热面积来增强变压器油的冷却效果.

参考文献：

[1]陈伟根,李孟励,孙才新,等.变压器绕组热点温度热电类比计算模型仿真分析[J].重庆大学学报,2010,33(12):8-13.

[2]江淘莎.基于底层油温的油浸式变压器热点估计方法研究[D].重庆:重庆大学,2009.

[3]路长柏.电力变压器绝缘技术[M].哈尔滨:哈尔滨工业大学出版社,1997:125-153.

[4]江淘莎,李剑,陈伟根,等.油浸式变压器绕组热点温度计算的热路模型[J].高电压技术,2009,35(7):1 635- 1 639.

[5]杨建华,吴吉.变压器绕组温度场的研究[J].江苏电机工程,2007,26(3):24-26.

[6]黄晓峰,周利军,吴广宁.变压器热点温度计算经典模型的对比分析及改进[J].现代电力,2013(3):69-05.

[7]刘焕志,李扬,柏瑞,等.变压器温度场的有限元分析[J].电力技术,2003,27(3):63-77.

(编辑桂金星)

Numerical Calculation and Analysis of Oil-immersed Transformer Winding Temperature Field

ZHOU Jianchong1, LONG Hui1, HU Taotao1, LI Zhong1, ZHANG Xiaoqun1, CHEN Jiong2, XUE Fei2

(1. Ziyang Power Supply Company, Sichuan Electric Power Company, State Grid,Ziyang641300, China;

2. School of Electrical Engineering, Shanghai University of Electric Power, Shanghai200090, China;)

Abstract:Based on the boundary condition of transformer’s oil parameter and transformer radiation heat loss,ANSYS is used to conduct simulation analysis of a 630 kW/10 kV transformer with nature cycle-oil cooling method.A conclusion can be made from simulation result that with the increase of load,the winding temperature increases sharpest,and hot spot is located at the 85% vertical height.

Key words:oil-immersed transformer; hot spot temperature; numerical calculation

中图分类号：TM411

文献标志码：A

文章编号：1006-4729(2015)06-0551-05

通讯作者简介：周建聪(1973-),男,高级工程师,四川仁寿人.主要研究方向为电力系统.E-mail:184061072@qq.com.

收稿日期：2015-05-19

DOI：10.3969/j.issn.1006-4729.2015.06.011