二叉树多分类SVM在目标分群中的应用

段同乐，张冬宁

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)



二叉树多分类SVM在目标分群中的应用

段同乐，张冬宁

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

摘要为了解决目标分群问题，在研究目标关键属性的基础上，提出一种基于二叉树多分类支持向量机(SVM)的目标分群方法。介绍了基于统计学习理论的支持向量机方法的基本原理和算法本身的理论优势，由于支持向量机的本质是解决二分类问题的，因此如何建立支持多分类的支持向量机是研究的关键。采用基于二叉树的多分类支持向量机算法，建立了解决目标分群问题的算法模型，将分类器分布在各个节点上，从而构成了多分类的支持向量机。将算法进行软件实现，并利用模拟数据对支持向量机进行了训练，调整支持向量机参数，得到了较好的分群结果，证明了该方法的有效性。

关键词目标分群；二叉树；支持向量机；统计学习理论

0引言

目标分群是二级数据融合的关键步骤。在综合考虑目标位置、属性和运动状态等信息的基础上，将类型相近、运动状态相近、执行相同任务或具有相同威胁的目标进行合并，简化对象域情况，给指挥员提供简单明了的视图[1]。

分群的基本思想是对可用数据进行分组,目前已经有很多目标分群方法研究[2]，如层次聚类、K均值动态聚类和神经网络等，这些方法共同的理论基础之一是统计学。传统统计学研究的是样本数目趋于无穷大时的渐进理论，但在实际问题中，数据样本往往是有限的。统计学习理论(Statistical Learning Theory，SLT)是一种专门研究小样本情况下机器学习规律的理论[3,4]。

SVM是一种基于统计学习理论的机器学习方法[4]，由于其建立在结构风险最小化准则上，从而使得SVM分类器具有较好的推广能力[5]。但SVM本质上是一种二分类方法，而目标分群问题是一个多分类问题，将二类分类拓展到多类分类是目前SVM研究的热点问题[6]。本文提出基于二叉树多分类的支持向量机方法，将目标的属性空间定义为分类样本的特征空间，建立目标分群的分类模型，通过样本目标的学习训练，调整模型参数，得到了较为理想的分群结果。

1常用的SVM多类分类算法

1.1　SVM基本思想

支持向量机是Vapnik等根据统计学习理论提出的一种新的机器学习方法，其最大特点是根据Vapnik的结构风险最小化原则，尽量提高学习的泛化能力，即由有限的训练集样本得到的小误差仍能够保证对独立的测试集小的误差。另外由于支持向量机算法是一个凸优化问题，因此局部最优解一定是全局最优解，可防止过学习，这些特点是其他学习算法，如神经网络学习算法所不及的。对于分类问题，支持向量机可简述为：在线性可分的情况下，有很多线性分类器可以把2类样本分隔开，但是只有一个分类器能够使2类样本的分类间隔最大，这个线性分类器就是最优分类超平面，与其它分类器相比，具有更好的泛化性。对于非线性情况，首先，将输入空间中的样本通过某种非线性函数关系映射到高维特征空间中，使2类样本在此特征空间中线性可分；然后，在此特征空间中构造一个最优分类超平面。把2类样本没有错误地分开就是保证经验风险最小(为0)，使分类间隔的距离最大就保证置信范围最小，从而使真实风险最小，如图 1所示。

图1　SVM基本思想

目标分群问题在其特征空间中是线性不可分的，其最优分类超平面的判别函数为：

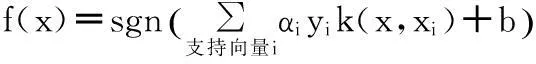
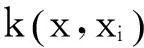
1.2　核函数的选择

核函数本质上是一种映射函数，能够将低维空间的非线性问题映射到高维空间中，变成线性问题进行处理，而计算复杂度并没有增加。常用的核函数有：

线性核函数(Linear function)

多项式核函数(Polynomial function)

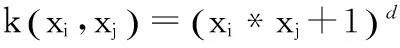
径向基核函数(Radial function，RBF)

Sigmoid核函数(Sigmoid function)

核函数的选择实际上是选择一组具有几个参数的核，比如径向基核函数中参数γ需要确定。并且，核函数的选择必须适用于具体的样本数据。当缺乏可靠的条件时，在应用中通过使用验证集或者交叉验证的方式来确定这些参数。

1.3　多分类SVM

将二分类SVM拓展到多分类SVM，本质就是将一个多分类SVM按照一定的方法分解成多个二分类SVM，通过求解多个二分类SVM，达到求解多分类SVM的目的。常用的多分类SVM方法有1-v-1算法[7]、1-v-r算法[7]和有向无环图算法[8]等。

1-v-1算法是对N类训练样本中的任意2类构造一个二类分类器，共构造N(N-1)/2个分类器。其优点是每个判别函数的支持向量数少，缺点是需要进行大量的二次规划计算，并且由于每次参与训练的样本只有2类，容易造成错误分类。

1-v-r算法是对N类训练样本中的每一类和其余样本构造一个二类分类器，共构造N个分类器。其优点是算法简单，容易实现，并且计算速度较快，缺点是由于每个二类分类器的正负样本规模严重不对称，容易产生无法分类的样本或属于多个类别的样本。

有向无环图算法构造二类分类器的方法和1-v-1算法一样，共构造N(N-1)/2个分类器，由于利用了图论中的有向无环图的思想，将测试样本输入根节点，每次判别排除最不可能的一个类别，经过N-1次后剩下的类别即为该样本所属的类别。其优点是速度优于1-v-1算法，缺点是没有考虑分类错误传递对后续分类产生的影响。

2基于二叉树多分类SVM的目标分群模型

2.1　二叉树多分类SVM算法

鉴于1-v-1算法、1-v-r算法和有向无环图算法的缺陷，本文采用二叉树多分类SVM算法来解决目标分群问题。二叉树多分类SVM算法有2种[9]。一种是在把N类中最相近的N-1类看作一类，余下的一类看作一类，构建一个二类分类器，进行分类。然后在N-1类中，取出最相近的(N-1)-1类看作一类，把N-1类中余下的一类看作另一类，构建第二个二类分类器。以此类推，直到最后两类，如图 2所示。对于N类问题，一共需要构建N-1个二类分类器。其优点是：① 构建的二类分类器较少；② 不会产生无法分类的样本或属于多个类别的样本；③ 重复训练的样本量少，训练和分类的速度较快。另一种是在每次分割成2个子类时，每个子类中可以包含多个类。本文采用第1种算法，即每次只分出一类。

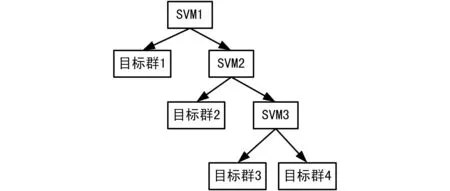
图2　二叉树多分类SVM分类过程

2.2　目标分群模型

对于目标分群问题，用二叉树多分类SVM算法进行求解的过程如下[10]：

① 将目标分群问题数据化。目标分群问题中，样本数据的特征包括：在某一时刻目标所处位置的经度、纬度、高度、航向、航速、目标的敌我属性、型号、类型和作战任务[11]，共9维。由于SVM本质上是基于距离进行分类的算法，因此需要将特征的表示方式转换为可距离化的数据。其中，经度、纬度、高度、航向及航速本身已数值化，但需要统一量纲；敌我属性、型号、类型和作战任务则需要数值化，即用数值表示语义。

② 对特征数据归一化。每个特征的取值范围有很大差异，为了避免大数值范围的特征主宰小数值范围的特征，需要对特征数据进行归一化，以降低支持向量对某些特征的过度依赖。归一化通常是将每个特征缩放到[-1，+1]或者[0，1]这个范围。

③ 选择核函数。本文采用RBF核函数。

④ 采用二叉树多分类SVM算法将目标分群问题转化为多个二分类问题。

算法分为训练和分类2个阶段，训练阶段的步骤如下：

步骤1:构造一个新的二叉树节点；

步骤2:计算目标群数量N；

步骤3:如果N>2则执行步骤4；如果N=2则转到步骤8；

步骤4:把目标集合分为两个子集TargetSetA和TargetSetB，TargetSetB为距离最相近的N-1个群中的目标集合，TargetSetA为余下的一个群中的目标集合；

步骤5:对TargetSetA中的目标标记为正类，TargetSetB中的目标标记为负类，用此二类目标训练一个二类SVM分类器；

步骤6：设定TargetSetA为叶子节点，其编号就为测试目标样本进入该节点时的分类编号；

步骤7:对TargetSetB重复步骤l到步骤3，进行下一次判断；

步骤8:对二类目标样本中的一个类别标记为正类，另一个类别标记为负类，训练一个二类SVM分类器；

步骤9:设定上述2类为叶子节点，其编号就为测试目标样本进入该节点时的分类编号；

步骤10:以训练好的二类SVM分类器作为二叉树中间节点，加上步骤6和步骤9中的叶子节点，构成二叉树。

分类阶段的算法如下：

步骤1:把测试目标数据输入二叉树结构的根节点；

步骤2:如果该节点不是叶子节点，则转入步骤3，如果是叶子节点则转入步骤6；

步骤3:把测试目标数据输入训练好的二分类SVM分类器，如果SVM分类器输出正值，则转入步骤4，输出负值则转入步骤5；

步骤4:进入该节点的左孩子节点，并转到步骤6；

步骤5:进入该节点的右孩子节点，并转到步骤2；

步骤6:直接得出该叶节点类编号为输入测试目标数据所属的群。

⑤ 用交叉验证的方法，确定RBF核中参数γ和惩罚因子C，从而得到最高的预测精度。

3软件实现效果

针对上述目标分群算法进行了软件实现。使用二维仿真数据来模拟红、蓝军空中目标的侦察巡逻场景。当所关注的区域里出现较多目标时，用户难以确定要关注的目标，在显示时也显得比较复杂凌乱，如图 3所示。图3中，以圆形符号表示红军，以三角符号表示蓝军。

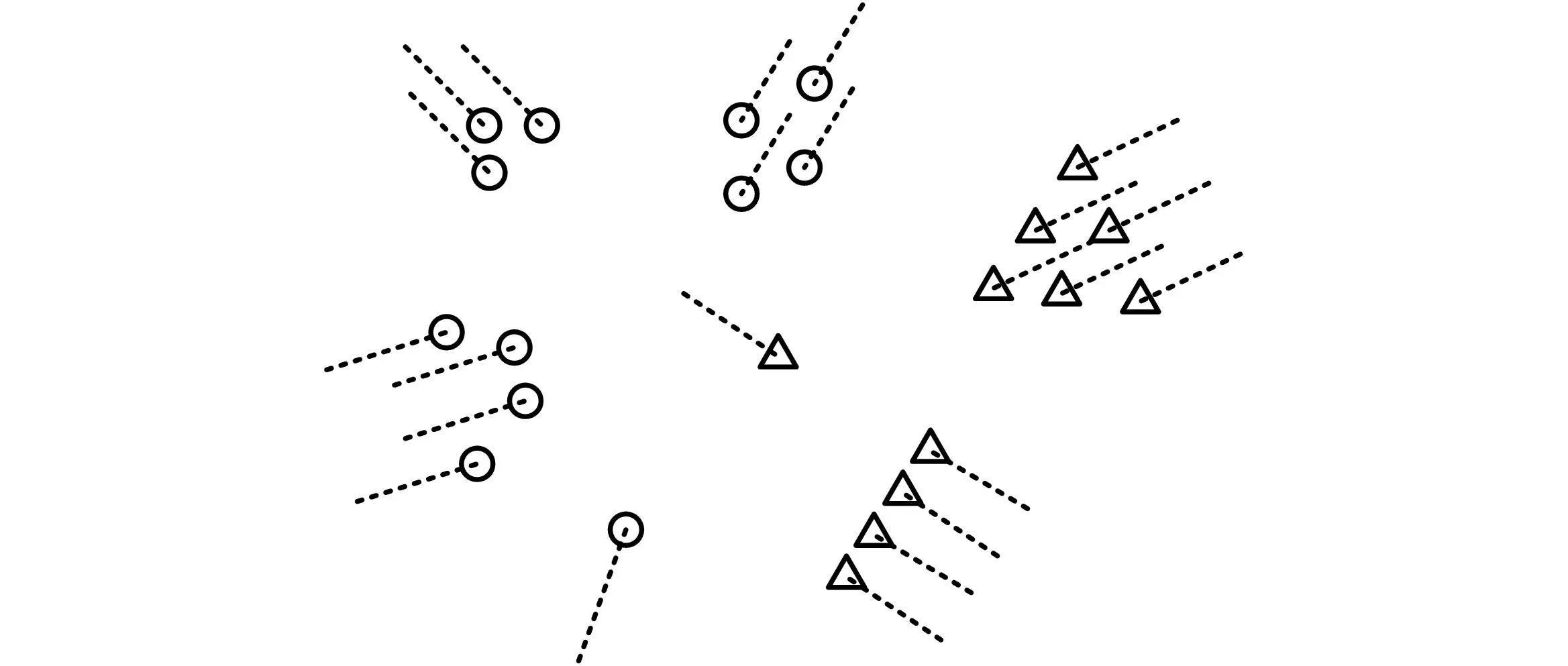
图3　仿真目标图形显示

经过对目标进行分群处理后，出现了3个红军目标群和2个蓝军目标群，对象环境中的重要情况可以由目标群的运动情况来判断得出。目标群的图形显示方式有2种：一种为在群中心上显示一个带方向的群符号，并用数字显示架次数，这种方式更利于简化整体态势展现，如图 4所示；另一种为显示群的外接多边形，这种方式有利于展现目标队形，如图 5所示。

图4　群中心简化图形显示

图5　群外接多边形图形显示

4结束语

对多目标对象进行分群处理，可以更加准确地掌握整体态势。以分群处理后的目标群显示对象环境信息，更加清晰，并且突出重点，使指挥员能够迅速掌握整体态势的发展状况。本文提出了一种适合目标分群问题的二叉树多分类的支持向量机方法，将统计学习的理论引入到数据融合中。由于目标分群的样本数据并不是海量的，因此建立在小样本机器学习基础上的统计学习理论是适用于目标分群问题的。经过软件实现显示，该方法能够有效地对多目标对象进行分群，值得进一步深入研究。

参考文献

[1]张芬,贾则,生佳根,等.态势估计中目标分群方法的研究[J].电光与控制,2008,15(4):21-23.

[2]龙真真,张策,王维平.基于层次聚类态势估计中的目标分群算法[J].弹箭与制导学报,2009,29(3):209-211.

[3]VAPNIK V N.The Nature of Statistical Learning Theory[M].New York:Springer-Verlag,1995:59-64.

[4]VAPNIK V N.统计学习理论的本质[M].张学工，译.北京:清华大学出版社,2000:85-125.

[5]张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-42.

[6]袁胜发,褚福磊.SVM多类分类算法及其在故障诊断中的应用[J].振动工程学报,2004,17(5):419-421.

[7]吕晓丽,李雷,曹未丰.基于二叉树的SVM多类分类算法[J].信息技术,2008(4):1-3.

[8]李昆仑,黄厚宽,田盛丰.一种基于有向无环图的多类SVM分类器[J].模式识别与人工智能,2003,16(2):164-168.

[9]唐发明,王仲东,陈绵云.支持向量机多类分类算法研究[J].控制与决策,2005,20(7):746-749.

[10]马笑潇,黄席樾,柴毅.基于SVM的二叉树多类分类算法及其在故障诊断中的应用[J].控制与决策,2003,18 (3):272 -276.

[11]卢文清,何加铭,曾兴斌,等.基于多特征提取和粒子群算法的图像分类[J].无线电通信技术,2014,40(2):90-93.

[12]韩顺杰,赵丁选.基于SVM的二叉树多类分类算法在工程车辆档位决策中的应用[J].中国公路学报,2007,20(5):122-126.

段同乐男，(1975—)，高级工程师。主要研究方向：智能信息处理。

张冬宁女，(1981—)，高级工程师。主要研究方向：智能信息处理、软件产品线。

Application of Multiclass SVM Based on

Binary Tree in Target Grouping

DUAN Tong-le,ZHANG Dong-ning

(The54thResearchInstituteofCECT,ShijiazhuangHebei050081,China)

AbstractSupport Vector Machines (SVMs) is originally designed for linear binary pattern recognition.Many multiclass SVMs are introduced briefly in the paper.Then the method of multiclass SVM based on binary tree is designed after analyzing the key issues of target grouping.The model of the multiclass SVM algorithm is designed.And the algorithm is realized by coding.The algorithm parameters and weighting factors are adjusted by simulation experiment.The result of simulation validates the feasibility and correctness of the grouping algorithm.

Key wordstarget grouping;binary tree;SVM;SLT

作者简介

基金项目：国家部委基金资助项目。

收稿日期：2015-03-05

中图分类号TP391.4

文献标识码A

文章编号1003-3106(2015)06-0088-04

doi:10.3969/j.issn.1003-3106.2015.06.24

引用格式：段同乐，张冬宁.二叉树多分类SVM在目标分群中的应用[J].无线电工程，2015，45(6)：88-91.