基于MATLAB的连续信号的采样与重构仿真分析

程建峰

(甘肃工业职业技术学院，甘肃 天水 741025)



基于MATLAB的连续信号的采样与重构仿真分析

程建峰

(甘肃工业职业技术学院，甘肃 天水 741025)

摘要针对连续信号的采样与重构问题，利用MATLAB仿真软件平台，仿真不同条件下连续信号的采样信号时域波形和采样后信号频谱、重构信号时域波形和重构后误差波形图。通过对采样周期对采样频谱叠加和信号重构精度的影响、以及信号被采样前后在频域的变化对比分析，得出在不同采样频率的条件下，对应采样信号的时域、频域特性以及重构信号与误差信号也随之产生变化，连续信号可以完全恢复过来。

关键词MATLAB；信号采样；频谱叠加；信号重构

0引言

连续信号的数据采样遵循采样定律[1-2]，满足ws≥2wm，其中ws为采样频率，wm为被测信号的上限截止频率。但在实际操作中，由于被测信号的复杂性和其他因素的限制，合理选取采样频率会存在一定的困难，由此产生的误差不易发现。本文利用MATLAB软件[3-4]仿真平台再现了采样信号与频谱，分析了两者关系，以此探讨影响采样周期的因素以及信号重构的可行性。

1信号采样与信号重构

1.1　信号采样

理想信号采样器可以看成是一个载波为理想单位脉冲序列δT(t)的幅值调制器，即理想采样器的输出信号e*(t)是连续输入信号e(t)调制在载波δT(t)上的结果[5]。

用数学表达式描述理想采样器调制过程，则有e*(t)=e(t)δT(t)，理想单位脉冲序列δT(t)可以表示为：

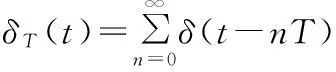
式中，δ(t-nT)是出现在时刻t=nT、强度为1的单位脉冲。由于e(t)的数值仅在采样瞬时才有意义，同时，假设e(t)=0∀t<0，所以e*(t)又可表示为：

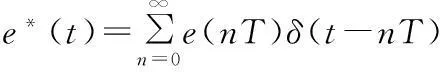
1.2　信号重构

设信号f(t)被采样后形成的采样信号为fs(t)，信号的重构是指由fs(t)经过内插处理后，恢复出原来信号f(t)的过程。若设f(t)是带限信号，带宽为ωm，经采样后的频谱为Fs(jω)。设采样频率ωs≥2ωm，现选取一个频率特性为：

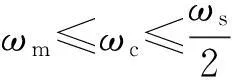
显然，F(jω)=Fs(jω)H(jω)，与之对应的时域表达式为：

f(t)=h(t)*fs(t)，

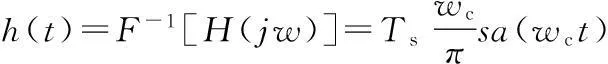
将h(t)及fs(t)代入得：

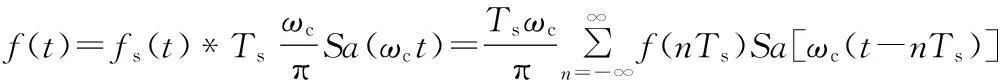
上式为f(nTs)求解f(t)的表达式。

通过分析，得到时域采样定理：一个带宽为ωm的带限信号f(t)，可唯一地由它的均匀取样信号fs(nts)确定，其中，取样间隔ts<π/ωm,该取样间隔又称为奈奎斯特间隔。根据时域卷积定理，求出信号重构的数学表达式为：

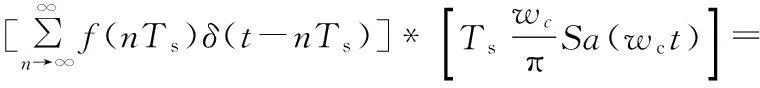
2仿真与分析

连续信号是指自变量的取值范围是连续的，且对于一切自变量的取值，除了有若干个不连续点以外，信号都有确定的值与之对应。MATLAB并不能处理连续信号，而是用等时间间隔点的样值来近似表示连续信号。当取样时间间隔足够小时，这些离散的样值就能较好地近似连续信号。时域对连续时间信号进行采样，是给它乘以一个采样脉冲序列，就可以得到采样点上的样本值，信号被采样前后在频域的变化，可以通过时域频域的对应关系分别求得采样信号的频谱[8]。

2.1　Sa(t)的临界采样及重构

当采样频率小于一个连续的同信号最大频率的2倍,即ws=2ωm时，称为临界采样。修改门信号宽度和采样周期等参数，得到的采样信号时域和频域特性，以及重构信号与误差信号的变化，如图1所示。

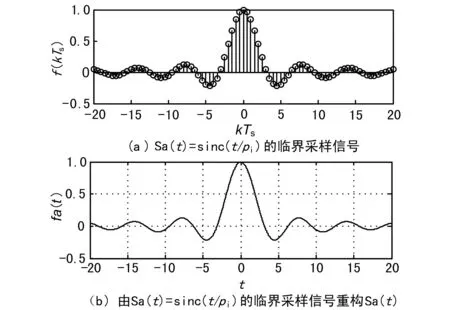
图1　Sa(t)的临界采样及重构图

为了比较由采样信号恢复后的信号与原信号的误差，可以计算出2个信号的绝对误差。当t选取的数据越大，起止的宽度越大。

2.2　Sa(t)的过采样及重构分析

当采样频率大于一个连续的同信号最大频率的2倍，即ws>2ωm时，称为过采样。在不同采样频率的条件下，观察对应采样信号的时域和频域特性，以及重构信号与误差信号的变化，如图2所示。

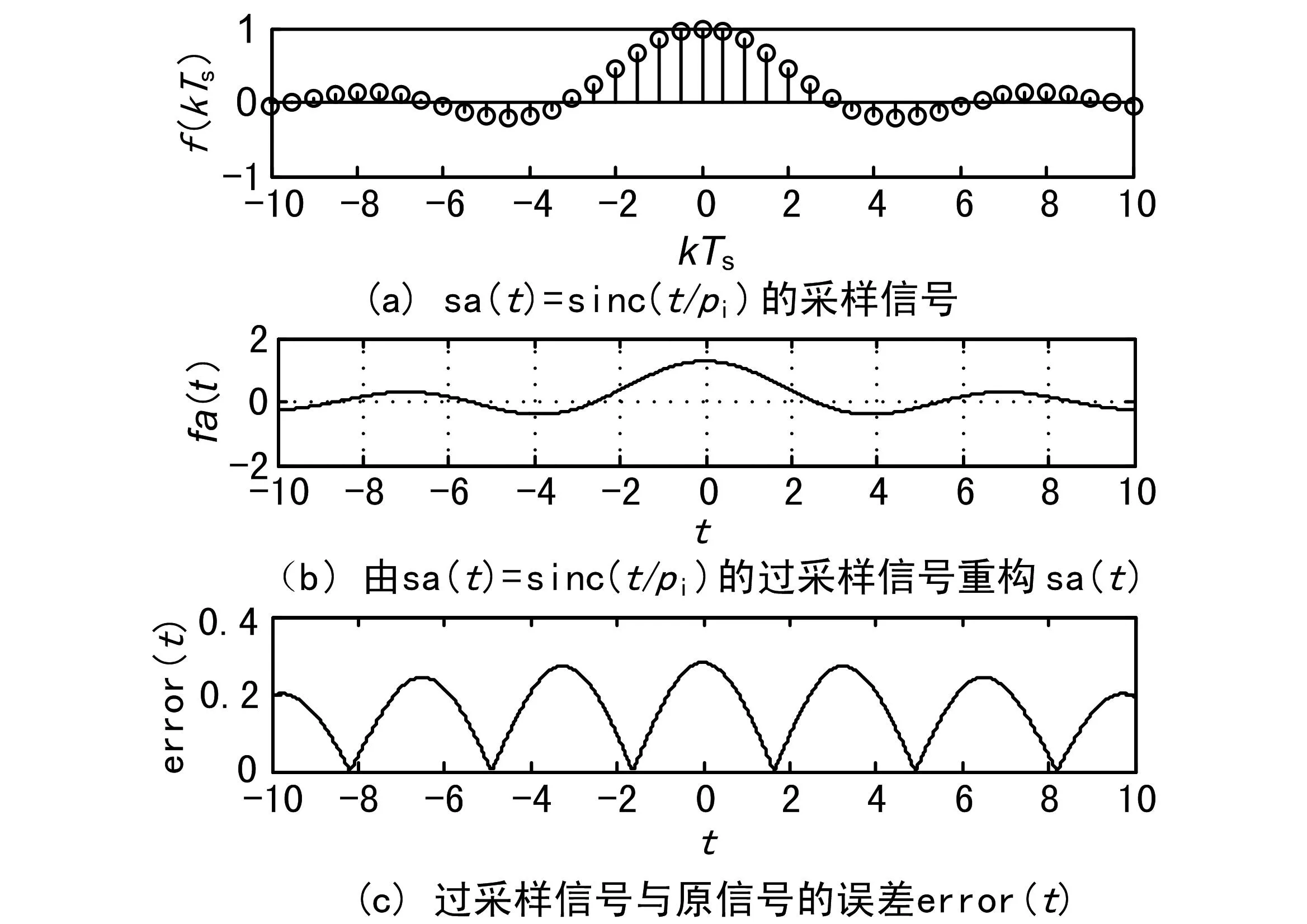
图2　Sa(t)的过采样信号、重构信号及两信号的绝对误差

从图2可看出将原始信号分别修改为抽样函数Sa(t)、正弦信号sin(20*π*t)+cos(20*π*t)、指数信号e-2tu(t)时，在不同采样频率的条件下，可以观察到对应采样信号的时域和频域特性，以及重构信号与误差信号的变化[9]。

2.3　Sa(t)的欠采样及重构分析

当采样频率小于一个连续的同信号最大频率的2倍，即ws<2ωm时，称为过采样。利用频域滤波的方法修改实验中的部分程序，完成对采样信号的重构，结果如图3所示。

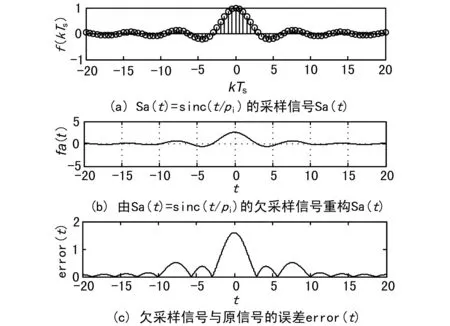
图3　Sa(t)的欠采样信号、重构信号及两信号的绝对误差

通过图3可以看出，绝对误差error已大为增加，其原因是因采样信号的频谱混叠，使得在|ω|<ωc区域内的频谱相互“干扰”所致。

3结束语

利用MATLAB所生成的临界采样、过采样和欠采样3种状态下的采样信号、重构信号及两信号的绝对误差图，可以直观地看到在不同采样频率的条件下，对应采样信号的时域、频域特性以及重构信号与误差信号也随之产生变化，一个连续时间信号完全可以用该信号在等时间间隔上的瞬时值来表示[10]，并且可以用这些样本值把信号完全恢复过来。

参考文献

[1]梁虹，梁洁，陈跃斌．信号与系统分析及其MATLAB实现[M].北京：电子工业出版社，2002.

[2]周利清，苏菲． 数字信号处理基础[M].北京：北京邮电大学出版社，2005.

[3]朱衡君．MATLAB语言及实践教程[M].北京：清华大学出版社,北京交通大学出版社，2009.

[4]骆文，赵强．MATLAB在信号与系统中的应用[J].数字技术与应用，2010(8)：23-25.

[5]陈永胜．基于信号频域特征实现位定时恢复[J].无线电通信技术，2014，40(2)：94-96.

[6]刘可．通用信号处理模块功能线程动态重构技术[J].无线电工程，2014，44(11)：77-80.

[7]余恺，李元实，王智．基于压缩感知的声音信号采集方法[J].仪器仪表学报，2012(1)：105-112.

[8]林从客，谢求成．一个时限信号采样定理及其在数据压缩中的应用[J].南京航空航天大学学报，1997(4)：29-45.

[9]夏辉，靳晓艳．相关运算在信号处理中的应用[J].无线电工程，2014,44(9)：67-69.

[10]艾名舜．多线性调频信号瞬时频率估计快速算法[J].无线电通信技术，2014，40(6)：36-39.

程建峰女，(1979—)，讲师。主要研究方向：通信和EDA技术。

Simulation and Analysis of Continuous Signal Sampling and

Reconstruction Based on MATLAB

CHENG Jian-feng

(GansuIndustryPolytechnicCollege,TianshuiGansu741025,China)

AbstractTo address the issue of continuous signal sampling and reconstruction,the continuous signal’s sampling signal time domain waveform and signal spectrum after sampling,the reconstruction signal time domain waveform and the error waveform after reconstruction are simulated under different conditions using the MATLAB simulation software platform.Through an analysis on the influence of sampling period on the sampling spectral overlay and signal reconstruction accuracy,and through a comparison between the signals before and after sampling in frequency domain,it is concluded that under different sampling frequencies,the corresponding sampling signal’s time domain,frequency domain characteristics,and the reconstruction signal and the error signal also vary,and the continuous signal can be completely recovered.

Key wordsMATLAB;signal sampling;spectrum overlay;signal reconstruction

作者简介

基金项目：甘肃工业职业技术学院项目(Gzy2011-27)。

收稿日期：2015-03-13

中图分类号TN911.7

文献标识码A

文章编号1003-3106(2015)06-0035-03

doi:10.3969/j.issn.1003-3106.2015.06.10

引用格式：程建峰.基于MATLAB的连续信号的采样与重构仿真分析[J].无线电工程，2015，45(6)：35-37.