基于VSIE的电磁散射问题的有效分析

梁　涛，陈佳林，钟雷声

(1．海军装备部装备采购中心，北京100071；

2．海军装备研究院，上海 200436)



基于VSIE的电磁散射问题的有效分析

梁涛1，陈佳林2，钟雷声2

(1．海军装备部装备采购中心，北京100071；

2．海军装备研究院，上海 200436)

摘要体面积分方程方法在金属介质混合结构电磁散射问题的求解方面具有较大优势，将重叠型区域分解法(ODDM)引入体面积分方程方法(VSIE)，实现了基于重叠型区域分解法的体面积分方程方法，为进一步提高效率，引入多层快速多极子方法(MLFMA)，实现两种快速算法在VSIE上的结合。通过几个算例，验证了这种算法占用内存小、迭代速度快，计算结果准确，具有分析复杂目标电磁散射问题的能力。

关键词体面积分方程方法；电磁散射；重叠型区域分解法；多层快速多极子方法

0引言

体面积分方程(VSIE)的求解基于矩量法(MoM)，矩量法在分析电磁辐射或散射问题中有着广泛的应用[1]。矩量法所产生的矩阵是满阵，存储量的量级是矩阵阶数的平方O(N2)，直接法求逆的计算量是矩阵阶数的立方，即O(N3)，迭代求解的计算量是O(N2)[2]。对于电大尺寸目标而言，无论是存储量还是计算量上，现有计算机资源都难以满足需求。重叠型区域分解法将整个求解域划分为几个子域，并通过循环求解子区域来得到整个区域的解。由于每次只求解一个子区，因而能节省计算资源。多层快速多极子算法(MLFMA)[3-5]是一种在多个层级分组，层间嵌套，逐层递推来实现的快速多极子算法。多层快速多极子方法能将计算机的存储量及计算复杂度进一步降低到O(NlogN)[6-8]。本文将重叠型区域分解法(ODDM)和多层快速多极子方法(MLFMA)同时加入体面积分方程法中，得到了改进算法(VSIE-ODDM-MLFMA)，数值算例结果证明了该方法的正确性和有效性，具有分析复杂目标电磁散射问题的能力。

1公式推导

1.1　VSIE概述

VSIE的基本思想是利用面等效原理和体等效原理把金属面用面电流代替，介质体用体电流代替，两个独立的等效电流同时满足面积分方程和体积分方程，然后用矩量法来求解。面积分方程作用在金属区域，而体积分方程作用在介质区域[9，10]。对面积分方程进行离散的基函数为RWG基函数[1]，对体积分方程进行离散的基函数为SWG基函数[11]。在金属介质混合结构的电磁散射问题中，体面积分方程的复合形式可表示为：

(1)

(2)

可对式(1)和式(2)进行基函数离散，然后利用矩量法进行求解。

1.2　ODDM的基本原理

若将整个求解区域分为若干个子区域，则对应的阻抗矩阵Z也被分为若干个子矩阵，然后分别求解子矩阵方程，再通过迭代求解得到整个区域的解，这便是区域分解法的思想基础[12，13]。由于每次只对一个子矩阵进行求解，所以降低了内存消耗。

若子区域没有重叠部分，则得到的分块矩阵相互之间无公共元素。从电流角度来看，分区边界有奇异效应出现，这样会导致算法效率不高，甚至不收敛。为抑制电流的奇异性，Brennan等[14]将子区域边界附近区域作为该子区的缓冲区，并将缓冲区与子区域作为整个求解区域来计算电流，然后舍弃缓冲区电流并保留子区域的电流，最后循环求解得到整个区域电流，这就是ODDM的原理。

1.3　VSIE-ODDM方法推导

用介质体极化电流JV和金属面电流密度JS表示式(1)和式(2)中的磁矢量位与电标量位，得到以JV和JS为自变量的入射场表达式。为便于推导VSIE-ODDM的递推公式，采用算子F简化该表达式，上两式可重新写作：

(3)

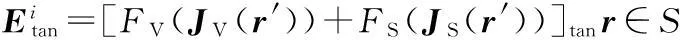
(4)

为了建立子区域之间积分迭代公式，定义2个关于JV和JS的线性算子，对于体积分式(3)有：

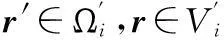
(5)

(6)

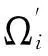
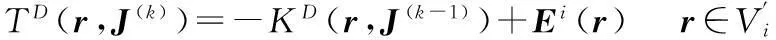
(7)

同理，定义和面积分方程(4)有关的2个算子TM(r,J)和KM(r,J)，则可获得混合结构中的面积分方程的重叠型区域分解迭代公式为：

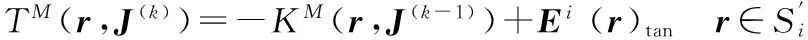
(8)

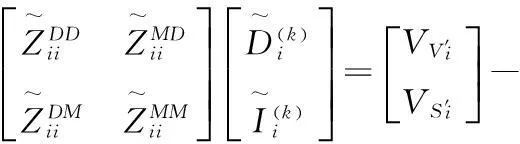
(9)

1.4　VSIE-ODDM-MLFMA方法

在区域分解法中将整个求解区域划分为迭代区和入射区，而在多层快速多极子的方法[2,15]中，又对整个求解区域进行了分层分组，因此对这两种方法进行结合时，必须同时考虑求解区域的划分和分组问题。

如果在多层快速多极子方法的某一层中，某个组至少存在一个基函数单元位于第i个迭代(入射)区中，那么就说该组属于第i个迭代(入射)区。因此值得注意的是有的组既属于迭代区又属于入射区。在ODDM-MLFMA中，必须根据以上原则分别建立迭代区和入射区的八叉树，方法是通过逐层剔除入射区上的元素来获得迭代区的八叉树，因此迭代区的八叉树和入射区的八叉树是整个区域八叉树的分支。

在此基础上，便可方便地在ODDM的基础上运用MLFMA。与MLFMA相比，ODDM-MLFMA聚合、转移、配置的对象发生变化。

2数值算例

算例1计算一个介质涂敷球结构。金属球半径为0.342 3λ0，涂层厚度为0.101 7λ0，相对介电常数为εr=2，平面波为垂直照射到结构上。将目标分成4个区域，分别对介质和金属进行四面体与三角形网格离散，其中SWG基函数的个数为14 332，RWG基函数的个数为963。

VSIE-ODDM-MLFMA和Mie级数计算所得的双站RCS的比较结果如图1所示。从图1中可以看出VSIE-ODDM-MLFMA计算金属介质混合结构的结果和解析解是比较吻合的，说明了程序的有效性。

图1　涂敷球的双站RCS

算例2计算一个上表面覆盖一层金属平板的介质长方体，介质的相对介电常数为1.6，目标结构尺寸如图2所示。

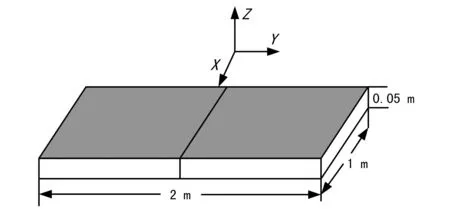
图2　金属介质混合结构

利用区域分解法进行计算时，将目标沿x轴平均分为两个区域，产生的SWG基函数的个数为4 323，RWG基函数个数为636，所以总共的基函数个数为4 959。仿真结果如图3所示。

在VSIE-ODDM-MLFMA计算中，只经过5次外迭代就达到收敛精度，收敛精度为9.001×10-4，而VSIE-ODDM经过第5次外迭代后所到达的收敛精度为1.006×10-3，比VSIE-ODDM-MLFMA略慢。在内存方面，VSIE-ODDM-MLFMA所占的内存仅占VSIE-ODDM所需内存的20.4%，表明了采用MLFMA后在节省内存方面的效果明显，如表1所示。

图3　金属介质混合结构的双站RCS

迭代次数VSIE-ODDMVSIE-ODDM-MLFMA12345610.3382.714×10-24.321×10-31.006×10-33.396×10-410.3362.820×10-24.178×10-39.001×10-4/

算例3计算平面FSS阵列结构，FSS单元为方环，方环外边长D1=7 mm，内边长D2=6 mm，方环周期为8 mm，阵列总大小为7×7。加载介质底板，介质长与宽都是56 mm，厚度0.5 mm，相对介电常数εr=3.0，求解频率在14 GHz，其结构示意图如图4所示。

图4　7×7平面FSS方环阵列及其单元示意图

目标分成4个非均匀区域，对介质和金属分别采用四面体和三角形剖分。SWG基函数的个数为30 213，RWG基函数的个数为1 372。垂直入射TM极化时其RCS计算结果与FEKO结果对比如图5，结果未归一化。

从图5可以看出，VSIE-ODDM-MLFMA分析FSS散射特性的结果与FEKO分析结果非常吻合，体现了该算法具有准确分析复杂目标电磁散射问题的能力。

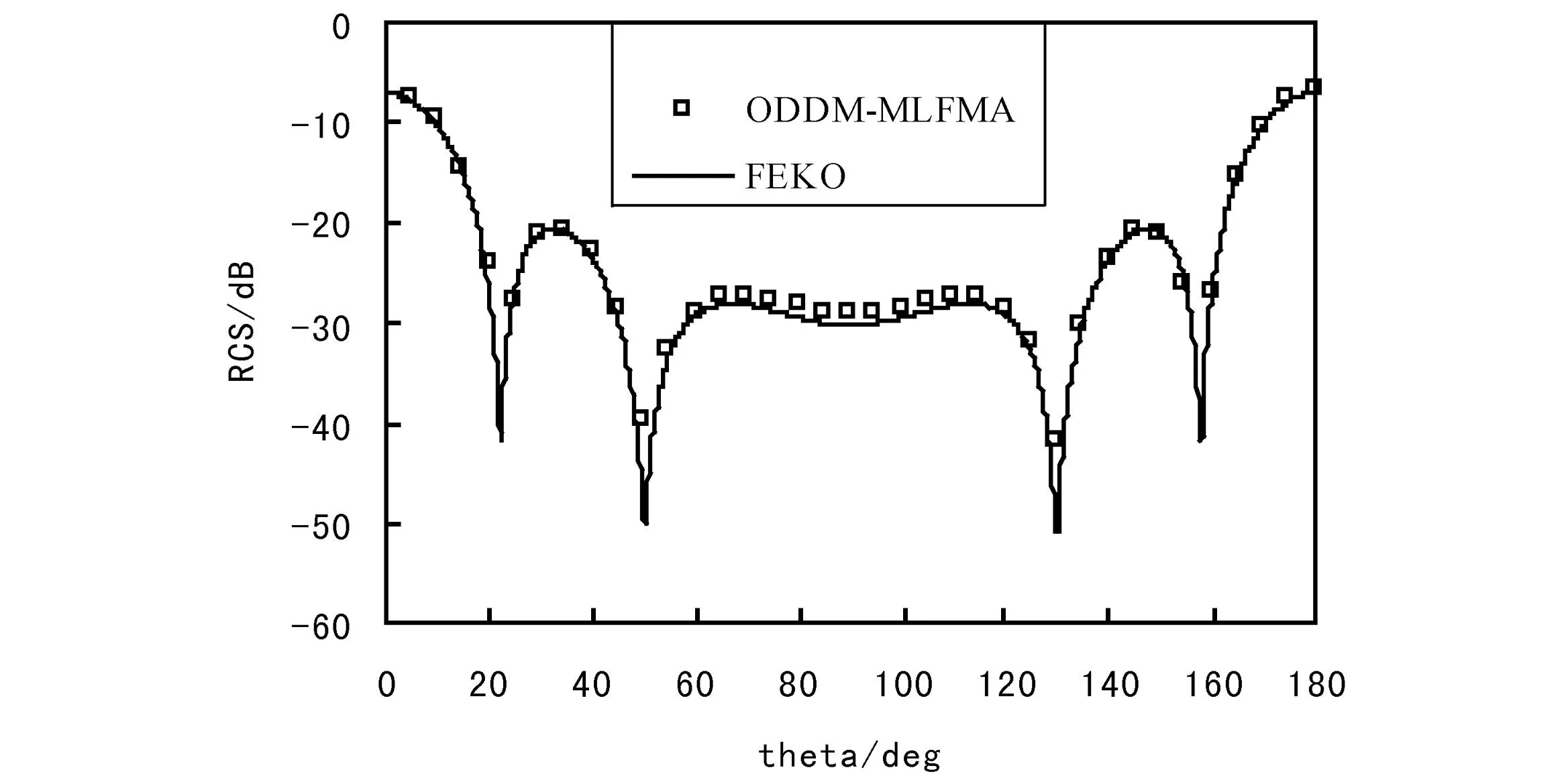
(a) φ=90°

(b) φ=0°图5　7×7平面FSS方环阵列双站RCS仿真结果

3结束语

本文将重叠型区域分解法和多层快速多极子算法成功引入体面积分方程方法，解决了硬件资源不足的问题，提高了求解效率，通过仿真实验验证，证明了该算法的可行性和有效性，具备分析复杂目标电磁散射问题的能力。

参考文献

[1]SADASIVA MR,DONALD R W ,ALLEN W G.Electromagnetic Scattering by Surface of Arbitrary Shape[J].IEEE Trans.Antennas Propagat.,1982,30(3):409-418.

[2]SHAO H,HU J,NIE Z,et al.Hybrid Tangential Equivalence Principle Algorithm with MLFMA for Analysis of Array Structures[J].Progress In Electromagnetics Research,2011,113:127-141.

[3]CUI Z W,HAN Y P,LI C Y,et al.Efficient Analysis of Scattering from Multiple 3-D cavities by Means of a FE-BI-DDM Method[J].Progress In Electromagnetics Research,2011(116):425-439.

[4]PING X W,CUI T J,LU W B.The Combination of BCGSTAB with Multifrontal Algorithm to Solve FEBI-MLFMA Linear Systems Arising from Inhomogeneous Electromagnetic Scattering Problems[J].Progress In Electromagnetics Research,2009,93:91-105.

[5]PENG Z,SHENG X Q,YIN F.An Efficient Twofold Iterative Algorithm of FE-BI-MLFMA Using Multilevel Inverse-based ILU Preconditioning[J].Progress In Electromagnetics Research,2009(93):369-384.

[6]SONG J M,LU C C,CHEW W C.Multilevel Fast Multipole Algorithm for Electromagnetic Scattering by Large Complex Objects[J].IEEE Trans.Antennas Propagat,1997,45(10):1 488-1 493.

[7]WALLÉN H ,SARVAS J.Translation Procedures for Broadband MLFMA[J].Progress In Electromagnetics Research,2005(55):47-78.

[8]ISLAM S,STIENS J,POESEN G,et al.Simulation and Experimental Verification of W-band Finite Frequency Selective Surfaces on Infinite Background with 3D Full Wave Solver NSPWMLFMA[J].Progress In Electromagnetics Research,2010(101):189-202.

[9]LU C C,CHEW W C.A Coupled Surface-volume Integral Equation Approach for the Calculation of Electromagnetic Scattering from Composite Metallic and Material Targets[J].IEEE Trans.Antennas Propagat.,2000,48(12):1 866-1 868.

[10]SHARK T K,RAO S M,DJORDIEVIC A R.Electromagnetic Scattering and Radiation from Finite Microstrip Structures[J].IEEE Trans.on Microwave Theory and Tech.,1990,38(11):1 568-1 575.

[11]SCHAUBERT D H,WILTON D R,GLISSON A W.A Tetrahedral Modeling Method for Electromagnetic Scattering by Arbitrarily Shaped Inhomogeneous Dielectric bodies[J].IEEE Trans.Antennas Propagat.,1984,32(1):77-85.

[12]TOSELLI A ,WIDLUND O.Domain Decomposition Methods—Algorithms and Theory[M].Berlin:Springer,2005.

[13]MARTINI E,CARLI G,MACI S.A Domain Decomposition Method Based on a Generalized Scattering Matrix Formalism and a Complex Source Expansion[J].Progress In Electromagnetics Research B,2010(19):445-473.

[14]BRENNAN C,CULLEN P,CONDON M.A Novel Iterative Solution of Three Dimensional Electric Field Integral Equation[J].IEEE Trans.Antennas Propagat.,2004,52(10):2 781-2 784.

[15]TABOADA J M,ARAJO M G,BÉRTOLO J M,et al.MLFMA-FFT Parallel Algorithm for the Solution of Large-scale Problems in Electromagnetics (invited paper) [J].Progress In Electromagnetics Research,2010(105):15-30.

[16]CHEN R S,YUNG E K N,CHAN C H,et al.Application of SSOR Preconditioned Conjugate Gradient Algorithm to Edge-FEM for 3-dimensional Full Wave Electromagnetic Boundary Value Problems[J].IEEE Trans.on Microwave Theory and Tech.,2002,50(4):1165-1172.

[17]ENGHETA N,MURPHY W D,ROKHLIN V,et al.The Fast Multipole Method (FMM) for Electromagnetic Scattering Problem[J].IEEE Trans.Antennas Propagat,1992,40(6):634-641.

梁涛男，(1976—)，硕士，工程师。主要研究方向：航空电子。

陈佳林男，(1986—)，博士，工程师。主要研究方向：航空电子。

Efficient Analysis of Electromagnetic Scattering

Problems Based on VSIE Method

LIANG Tao1,CHEN Jia-lin2，ZHONG Lei-sheng2

(1．ProcurementCenterofNavalArmamentDepartment,Beijing100071，China;

2．NavalAcademyofArmament,Shanghai200436,China)

AbstractThe volume-surface integral equation (VSIE) method has the advantage in solving electromagnetic scattering problems involving complex metal and dielectric mixed structure.In this paper,a method combining VSIE with overlapped domain decomposition method (ODDM) is used to analyze electromagnetic scattering problems successfully and efficiently.To further improve efficiency,multilevel fast multipole algorithm (MLFMA) is adopted,and then a novel VSIE-ODDM-MLFMA is proposed.Numerical results show that the proposed method has low memory requirement,fast convergence,and accurate simulation result.It is obvious that the proposed method has the ability to analyze the electromagnetic scattering problems of complex targets.

Key wordsvolume-surface integral equation；electromagnetic scattering；overlapped domain decomposition method；multilevel fast multipole algorithm

作者简介

收稿日期：2013-03-12

中图分类号TN801

文献标识码A

文章编号1003-3106(2015)06-0063-04

doi:10.3969/j.issn.1003-3106.2015.06.17

引用格式：梁涛，陈佳林，钟雷声.基于VSIE的电磁散射问题的有效分析[J].无线电工程，2015，45(6)：63-66.