基于FPGA的双模式伺服控制算法的研究
宋军,严东
(解放军92941部队,辽宁葫芦岛125001)
基于FPGA的双模式伺服控制算法的研究
宋军,严东
(解放军92941部队,辽宁葫芦岛125001)
舰炮的伺服系统主要根据火控系统给出的目标参数,完成炮塔的旋转和目标的跟踪。伺服系统的响应性能直接关系到作战系统的性能和可靠性,而控制算法是伺服控制的核心之一。提出了一种基于双模式融合的bangbang-PID控制算法。同时,针对传统基于软件的实现方式存在响应速度滞后、设备体积大、抗干扰性差等问题,提出了基于FPGA技术的控制算法实现方案。实验结果表明,该算法具有较快的响应速度,可以较好地满足伺服系统的要求。
舰炮伺服系统,双模式融合,控制算法,FPGA
0 引言
随着舰炮要应对目标的移动速度和方位变化等性能不断的提高,对舰炮伺服系统的响应速度和精度提出了越来越高的要求。采取单一模式的控制方式已不能较好地满足伺服系统的需求,而过于复杂的控制算法在提升准确度的同时,将对系统的响应速度造成影响。因此,探索高效、准确的控制算法成为提升舰炮伺服系统性能的关键问题之一。
目前舰炮的伺服系统多采取PC+DSP或PC+单片机的平台,采用软件实现的方式,虽然能够满足目前的需求,但随着系统小型化的发展趋势和抗干扰需求的不断增加,当前所采用的实现方式所暴露出的体积大、功耗高、抗干扰能力差的问题一定程度上降低了舰炮伺服系统的集成度,以及在复杂电磁环境下的作战性能。
基于以上存在的问题,本文提出了一种双模式融合的控制算法,即bangbang-PID算法,并给出了该算法性能的对比仿真测试;同时,结合目前最新的可重构技术,采用FPGA平台,对控制算法进行了设计实现,硬件测试结果进一步验证了算法的高效性。
1 双模式融合的控制策略
1.1 增量PID控制
增量PID是指数字控制器的输出只是控制量的增量。由式(1)可以看出,位置PID控制算法是由输出量直接控制执行单元,输出值与执行元件的位置直接对应。位置PID的控制算法的输出量U(k)与过去的状态有关,要对e(k)作累加计算,计算量大。而且,当系统出现故障时,e(k)的大幅变化将会引起输出量的大幅变化,导致执行元件的大幅变化,会造成严重后果。由式(1)可以推导出式(2):
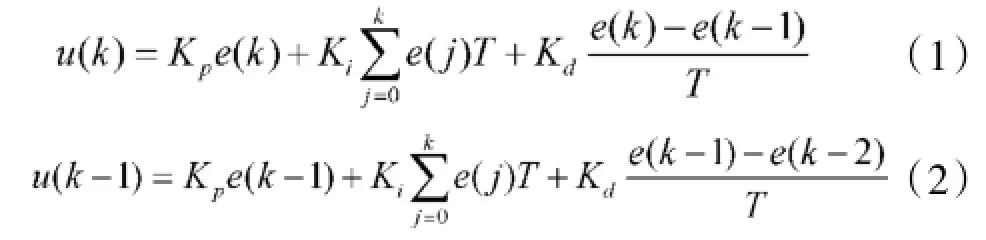
将两者相减可得式(3):
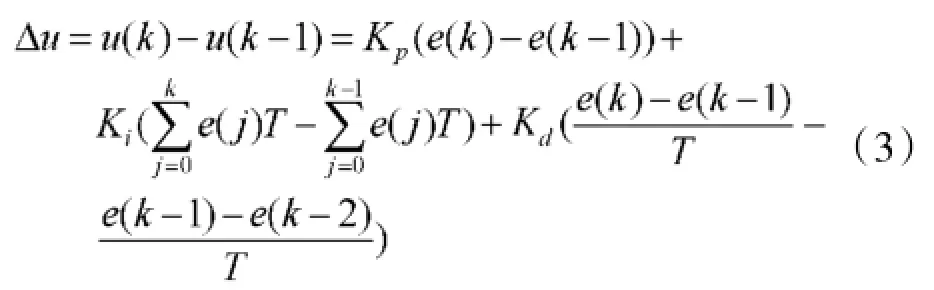
整理后可得:
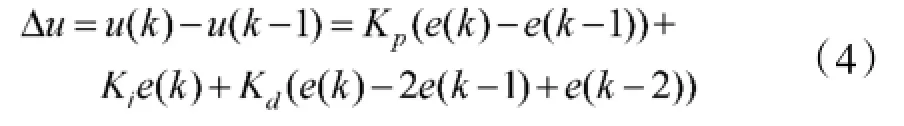
由式(4)可以发现增量PID已找不出调节作用对位置绝对信息的作用,仅针对当前调整量的反馈进行处理。增量式PID控制算法,除了与本身调控性能相关的Kp、Ki、Kd参数外,只涉及最近的3个误差采样值e(k)、e(k-1)、e(k-2),即可以实现PID控制。
因此,增量PID具有如下2个特征:①位置式PID控制与过去系统的整个状态有关,涉及到以前的误差累加值;而增量式PID与最近三次误差有关,因此,系统累计误差基本对增量PID控制器没有影响。②增量式PID输出为控制量增量,若被控系统出现故障,由于一般伺服系统具有记忆功能,调整误差影响较小,不会造成严重影响。
1.2 Bang-Bang控制
Bang-Bang控制是一种特殊的最优控制[1-2],其特征为不断地从一个控制边界切换到另一个控制边界值,即开关控制。
Bang-Bang控制的求解问题模型如式(5)所示:
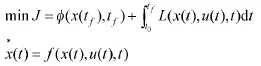
其中,
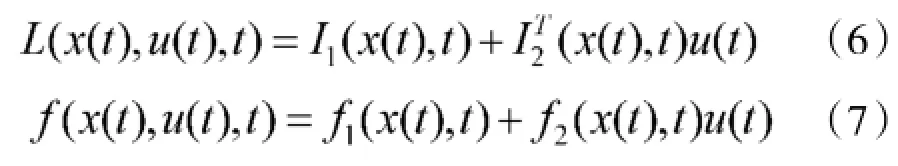
x(t)∈Rd(x)表示d(x)维的状态向量,u(t)∈Rd(u)表示d(u)维的控制向量,I2∈Rd(x),f2∈Rd(x)d(u)。
由Hamilton函数
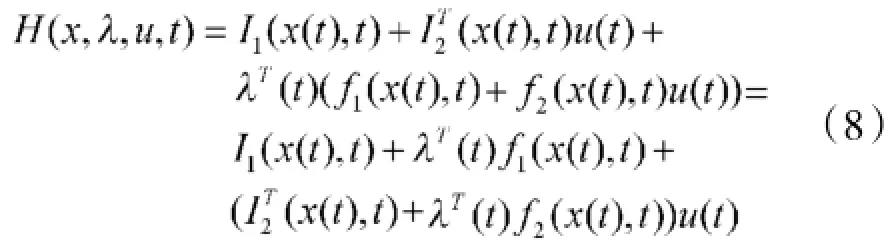
定义切换函数,如下所示
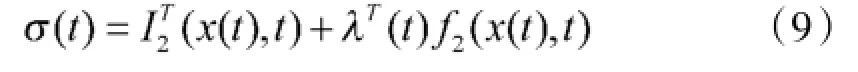
根据Pontryagain极小值原理,若保证Hamilton函数全局最小,即σ(t)u(t)≤σ(t)(t),需要满足如下条件。
当σi(t)>0,应取ui=umin,i。这时,H全局最小(从ai≤ui(t)≤bi中取最小的ui,即取umin,i,使σi(t)ui为最小的正数,从而使H全局最小)。
当σi(t)<0,应取ui=umax,i。这时,H全局最大(从ai≤ui(t)≤bi中取最大的ui,即取umax,i,使σi(t)ui为最小的负数,从而使H全局最大)。
当目标状态方程中含有线性控制项,且各分量为有界,可通过采取边界值实现开关控制的方案实现时间最优控制,即为Bang-Bang控制。
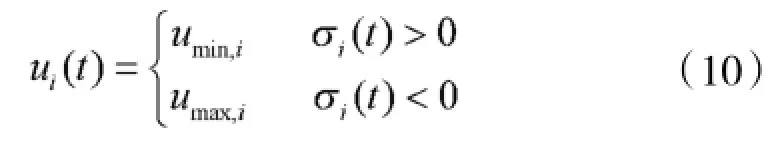
Bang-Bang控制是一个随偏差e正负变化的开关量输出装置[3-4],使得系统从一个初始状态到另一个状态的过渡时间最短,具有快速的上升速度和惯性,保证了系统的动态性能。
1.3 双模式融合控制策略
通过1.1节的论证可知,对于增量PID,当Kp,Ki,Kd 3个参数确定后,增量PID系统的调控性能即可确定,虽然Kp,Ki,Kd 3个参数在一定程度上影响增量PID控制的调控时间和调控幅度,但只要在合理的范围内,增量PID的调控曲线大体相同[5-8]。其后期调整具有较高的调控精度,从而减小了后期系统调整的频率,因此,对理想值与反馈值之间误差较小时,具有良好的微调效果。
在1.2节的论述证明了通过采取Bang-Bang控制机制能够使系统以最小的时间代价达预期值,即通过偏差e正负变化的开关量输出使得最优指标函数J成立。
在实际跟踪控制系统中,伺服系统需要完成快速、精准的定位,任何单一的控制方法都很难满足需求。综合Bang-Bang控制在早期的快速逼近优势和增量PID后期较高调整精度特点,本文将二者融合,提出了Bang-Bang增量PID的多模控制方案。
其双模控制状态如式(11)所示:
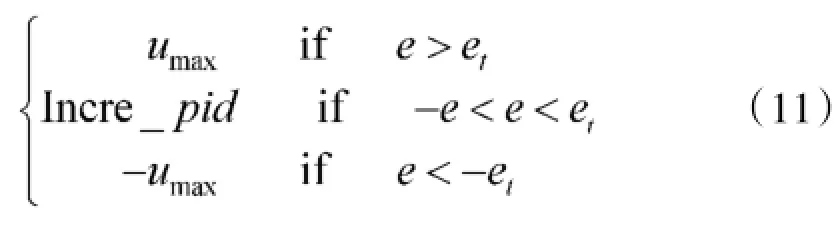
Bang-Bang增量PID控制器的工作原理为:根据实际的跟踪伺服系统的物理情况及跟踪角度调整方案,给出一个特定的误差极限值e,该误差极限值包含正负两种情况。这里以e>0为例说明。当输出反馈与目标值差值绝对值大于阈值e时,说明误差较大,应采用Bang-Bang控制策略,以时间最优的方式,提高跟踪伺服系统的响应速度,当误差绝对值小于阈值e时,说明此时系统反馈与目标值在一个合理空间中,此时,通过增量PID控制策略,以精度最优的方式,提供伺服系统的准确定位。
Bang-Bang增量PID控制器在控制初期,通过时间最优方式逼近目标区域,获得良好动态性能,在控制中后期,通过精度优先方式准确定位,获得较好的稳态性能。该方案完全满足跟踪伺服系统的速度及精度要求。如图1所示,在matlab中,采用模型分别为增量PID控制器、Bang-Bang控制器、Bang-Bang增量PID控制器的响应曲线。从图中可以看到,Bang-Bang增量PID在早期较增量PID有较大的超调,但逼近目标值时间更短,在中后期,较Bang-Bang具有更高精度,调整幅度较小。同时,Bang-Bang增量PID的响应时间为三者最小。
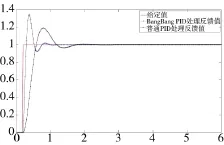
图1 响应曲线
2 基于FPGA的实现
为了进一步提高跟踪伺服系统的响应时间,本文采用FPGA[9-10],对Bang-Bang增量PID控制器,进行了硬件并行化。
图2为Bang-Bang增量PID控制器的原理图,图3为RTL级实现图。为了提高该控制器的灵活性,适应更多的应用及不同的伺服系统,本文将参数的设定采取可重构的方式,在给定默认值的情况下,允许用户进行修改。从图中可以看到,Bang-Bang增量PID控制器接口由12个输入信号和2个输出信号构成。
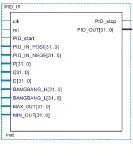
图2 控制算法原理图
为了说明控制器所涉及的信号类型和意义,以及方便后文中仿真说明,表1给出了算法模块的端口信号定义。
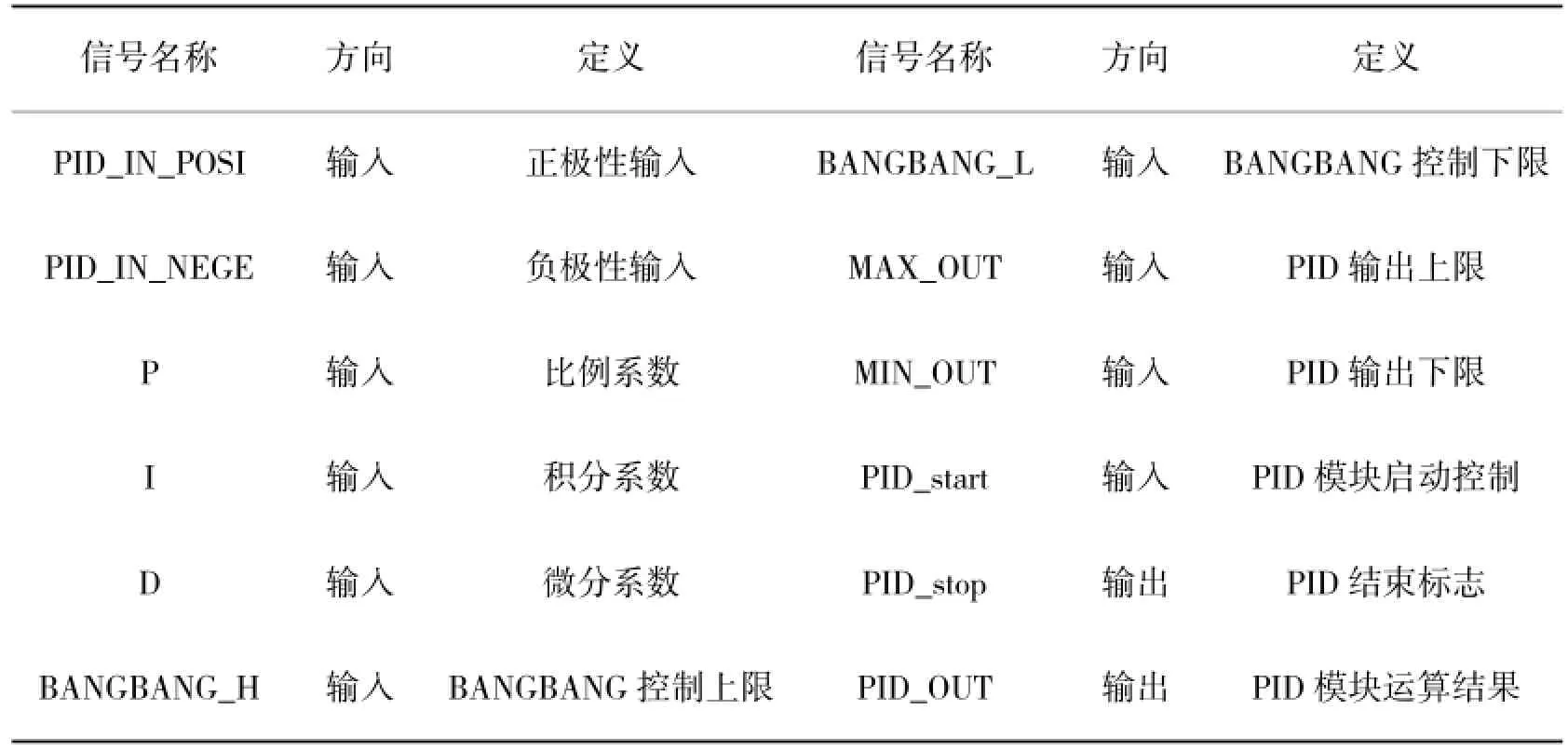
表1 端口信号定义
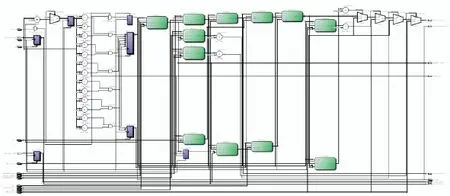
图3 控制算法RTL级实现图
3 功能测试
为了验证基于FPGA的双模式融合控制算法的性能,文中从以下3个方向展开了功能测试从3种情况展开,BangBang下限测试,BangBang上限测试,增量PID测试。
3.1 BangBang上限控制仿真
BangBang上限控制仿真的目的是为测试当控制器检测到反馈值与目标值误达到Bang-Bang控制上限时,控制器的信号输出情况。
PID_IN_POSI为8.0000000,PID_IN_NEGE为1.0000000;P为1.5000000,I为0.3,D为0。ERROR为0x40e00000,即浮点值7.0000000,因为ERROR已经大于BANGBANG_H,因而BANGBANG上限控制使能,当PID_stop为高时,bangbang_h_en为1,PID_OUT的值为MAX_OUT即0x4120000,即10.00000。图为仿真结果,从图4中可以看到,仿真结果与预期值相同。
3.2 BangBang下限控制仿真
BangBang上限控制仿真的目的是为测试当控制器检测到反馈值与目标值误达到Bang-Bang控制下限时,控制器的信号输出情况。
PID_IN_POSI为8.0000000,PID_IN_NEGE为15.0000000;P为1.5000000,I为0.3,D为0。ERROR为0xc0e00000,即浮点值-7.0000000,因为ERROR已经小于BANGBANG_L,因而BANGBANG下限控制使能,当PID_stop为高时,bangbang_l_en为1,同时PID_OUT的值为MIN_OUT即0xc120000,即-10.00000。
图5为BANGBANG下限控制仿真结果,从图中可以看到,仿真结果与预期值相同。
3.3 增量PID控制仿真
由增量PID公式知,当表达式涉及比例项+积分项时,增量PID运算除涉及本次反馈值与目标值误差外,还涉及上一次的误差,因此,测试进行了两次仿真,第一次,初始条件为上一次仿真误差为0,第二次仿真中的上一次误差值使用第一次增量PID的误差累积。
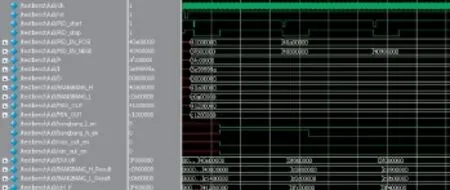
图4 BangBang控制上限仿真图

图5 BangBang控制下限仿真图
第一次PID运算的输入值PID_IN_POSI为5.0,PID_IN_NEGE为3.0;P为1.5,I为0.3,D为0.1。ERROR为2.0,比例项ctrl_P=ERROR×P=2.0× 1.5=3.0;积分项ctrl_I=ERROR×I+last_ctrl_I=2.0× 0.3+0=0.6;微分项ctrl_D=(ERROR-last_error)×D=(2-0)×0.1=0.2;PID_OUT_TEMP=ctrl_P+ctrl_I+ ctrl_D=3.0+0.6+0.2=3.8。因为3.8在溢出允许的范围内,所以当PID_stop为高后,PID输出运算结果0x40 733 333。
第二次PID运算,输入值PID_IN_POSI为5.0,PID_IN_NEGE为4.0;P、I和D仍保持上次的值。ERROR为1.0,比例项ctrl_P=ERROR×P=1.0× 1.500 000 0=1.5;因为上次PID运算结果使得
last_ctrl_I的值更新为0.6,所以积分项ctrl_I=ER ROR×I+last_ctrl_I=1.0×0.3+0.6=0.9;因为上次PID运算结果使得last_error的值更新为2.0,所以微分项ctrl_D=(ERROR-last_error)×D=(1-2)×0.1=-0.1;PID_OUT_TEMP=ctrl_P+ctrl_I+ctrl_D=1.5+0.9-0.1= 2.3。所以当PID_stop为高后,PID输出运算结果0x40 133 334。从图6中可见,仿真结果与理论运算结果相同。
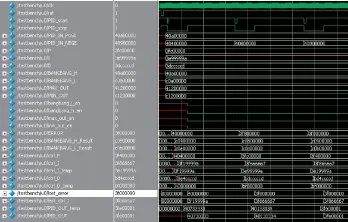
图6 增量PID控制仿真图
4 结论
本文针对舰炮伺服系统中控制算法这关键问题,提出了一种双模式融合的控制算法即bangbang-PID算法,该算法将响应过程分为3个处理阶段,当系统采取到的反馈值在处理上限和下限范围外时,采取bangbang控制策略,达到时间最优控制的目的;当反馈值在上限和下限之间时,采取增量PID控制策略,实现控制精度最优的目的。文中采用maltab工具,对双模式融合的bangbang-PID控制算法的收敛特性进行了仿真,结果显示,该算法具有响应速度快,收敛时间短的特征。
针对当前控制系统实现方式存在的问题,结合可重构技术,采用FPGA平台,对所提出的控制算法进行了设计和实现。该实现充分利用了硬件实现方式较软件方式具有抗干扰能力强、响应速度快的特性,进一步提升了舰炮控制系统的性能。同时,所实现的bangbang-PID控制核具有参数可配置的功能,可以根据不同型号的需求进行重新设置,具有较强的可移植性和适应性。
[1]赵斌,吴敏哲,梅占馨.单自由度系统的变结构滑模棒棒控制[J].力学与实践,1999,28(1):37-39.
[2]冯纯伯,张侃健,费树岷.自动化学报[J].1999,25(5):576-582.
[3]肖会芹.一种基于软切换的发动机转速智能控制算法[J].自动化与仪表,2010,25(4):37-42.
[4]王岩.变量泵控制变量马达系统建模及控制[J].控制理论与应用,2012,29(1):41-46.
[5]樊杰.基于车辆稳定性的电动助力转向系统控制算法研究[D].长春:吉林大学,2012.
[6]罗天资,陈卫兵,邹豪杰,等.直线电机模糊增量PID控制算法的研究[J].2011,30(2):56-60.
[7]赵勇,何宝福,余巍,等.基于增量式PID控制实现高精度跟踪机构设计研究[J].战术导弹技术,2009(1):66-69.
[8]姚栋伟,吴锋,杨志家,等.基于增量式数字PID的汽油机怠速控制研究[J].浙江大学学报,2010,44(6): 1122-1126.
[9]罗元.基于SOPC的PID控制器设计[D].武汉:武汉科技大学,2008.
[10]付学志,姚旺生,苟伟,等.基于FPGA的高速PID控制器设计与仿真[J].电子技术应用,2007(1):87-90.
Dual-mode Servo Control Algorithm Based on FPGA
SONG Jun,YAN Dong
(Unit 92941 of PLA,Huludao 125001,China)
Naval gun servo system is mainly based on the target parameters given by the fire control system to complete the rotation of the turret and target tracking.The response performance of the servo system is directly related to the operational performance and reliability of the system,and the control algorithm is one core of the servo control.This paper presents a bangbang-PID control algorithm based on dual-mode fusion,as well as presents a control algorithm based on FPGA technology to solve the speed of response lag,bulky equipment,and poor anti-interference problem of traditional software-based implementation.The experimental results show that the algorithm has a faster response speed,which can meet the requirements of the servo system better.
gun servo system,dual-mode fusion,control algorithms,FPGA
TB114.2
A
1002-0640(2015)01-0137-05
2013-11-05
2013-12-07
宋军(1978-),男,辽宁葫芦岛人,硕士。研究方向:舰炮武器系统试验与鉴定。

