热载荷下叶轮变形仿真分析

王水霞 张璞 张金娜/西安陕鼓动力股份有限公司

热载荷下叶轮变形仿真分析

王水霞 张璞 张金娜/西安陕鼓动力股份有限公司

0 引言

叶轮和主轴组装成的转子构成离心压缩机的心脏，其中大部分叶轮和主轴靠过盈连接来传递扭矩。随着工业装置大型化的发展和大型离心压缩机在石油、化工等领域广泛的应用，离心压缩机叶轮结构尺寸和工作转速在不断增大，过盈连接叶轮的过盈量也在增大。对某些结构的叶轮来说，实际热装加热温度采用传统的线性热胀理论公式计算的加热温度相差很大，这给生产制造带来不可控因素。温度是热装配前叶轮加热的重要的变量，温度的高低必须适宜，否则，不能顺利完成热装配。叶轮在热胀冷缩的物理规律作用下，当温度过低时，叶轮内孔的扩张变形量小于过盈量与装配间隙之和。在装配时，内孔与轴的外表面会产生接触摩擦，不仅会损坏内孔的结构与轴表面的粗糙度，还会产生过大的摩擦力，使热装配难以顺利完成。当温度过高时，叶轮内孔的热变形量过大，产生过大的热变形应力，当温度恢复到室温时，内孔难以恢复到原状态，破坏了内孔的可装配性与使用性。

本文利用有限元软件，仿真分析在热载荷下叶轮的温度、变形、应力分布情况，并将变形的仿真结果与线性公式计算结果比较，找出误差，从而为叶轮热装提供可靠的理论指导。

1 叶轮热装技术介绍

1.1 热装原理

热装前，叶轮内孔尺寸为Di，轴外径尺寸为Ds，轴尺寸比孔尺寸大Δr，Δr就是叶轮的设计过盈值，见图1（a）所示；装配时，将叶轮加热到一定温度，叶轮在热载荷的作用下，内孔热变形变大，若使叶轮装在轴上，安装时叶轮内孔必须大于轴外径，即必须保证有一定的安装间隙值e，则叶轮内孔需要的热变形量为ΔD=Δr+e，叶轮内孔尺寸变为Di+Δr+e，轴尺寸不变，如图1（b）；将轴装入叶轮内孔中，然后冷却降温，叶轮进行冷却收缩。在收缩的过程中，分两个阶段。自由收缩与约束收缩。自由收缩的阶段指从开始降温到轴开始与叶轮内孔壁接触这一段如图1（c）。在自由收缩的阶段，叶轮内孔仅在温度载荷作用下发生收缩，不受轴的向外支撑力。此时的Di+Δr表示自由收缩完成时叶轮内孔的直径，装配间隙e已在自由收缩阶段完全收缩掉。约束收缩是指叶轮内孔在收缩过程中，不仅仅受到温度载荷作用，还受到轴作用于内孔壁的向外压力。约束收缩完成时，温度冷却到装配环境的温度时，叶轮内孔实际直径Di+ζi，轴外径实际直径Di-ζs，如图1（d），表示叶轮冷却到装配前温度时，内孔直径并未恢复到装配前的Di，而是增大ζi，轴直径也发生了变化，而是减小了ζs。对比装配前后，叶轮增大的径向尺寸ζi为实际过盈值[1-2]。

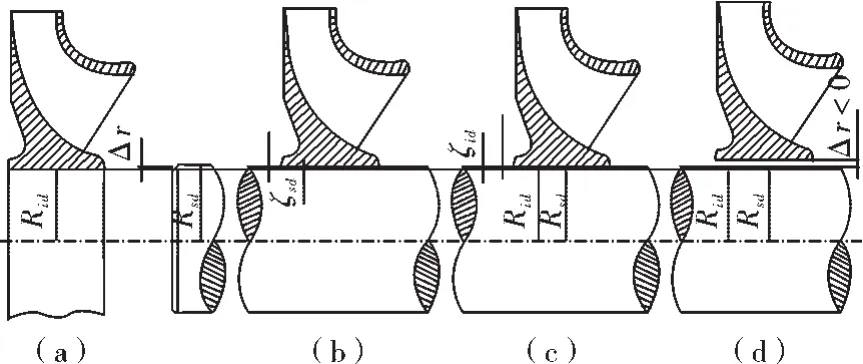
图1 轴和叶轮配合示意图

1.2 叶轮热装要求变形量的计算

叶轮热装前，其内孔比与其配合轴的轮毂须小某一值，即叶轮与轴配合的过盈值为e。防止叶轮内孔在装配过程中和轴发生碰撞，保证叶轮顺利热装，则叶轮内孔比与其配合轴的轮毂要大某一值，即安装间隙值δ。根据工程经验，本文取装配间隙δ为0.30mm[3]。那么，叶轮热装需要的变形量见式（1）

式中：δ为叶轮安装间隙值；e为过盈值；ΔD为叶轮热装需要的变形量。得：

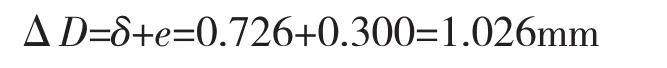
则该文中叶轮热装时，叶轮内孔需要1.026mm的变形量。

1.3 叶轮允许加热温度的分析计算

1）温度下限

叶轮加热的最低温度必须保证叶轮热变形大于最大过盈量与装配间隙之和，以使其顺利完成装配，不发生叶轮内孔与轴外表面发生碰撞。根据公式（2）

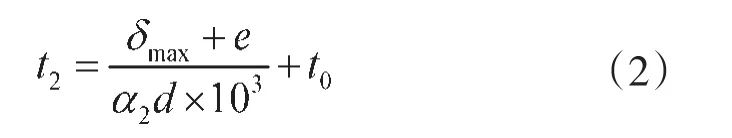
式中：δmax为所选标准配合在装配前的最大过盈值；e为避免装配时擦伤孔和轴的配合所需最小间隙；α2为轴的线胀系数；t0为装配时的环境温度；在运用温差装配法进行装配时，包容件的加热温度t2为：

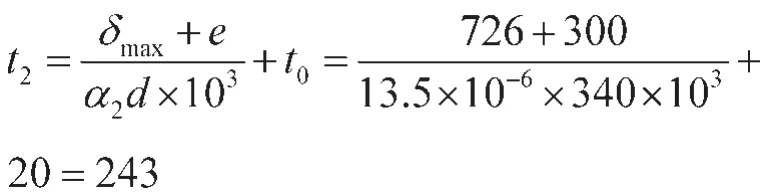
根据公式计算结果，要保证叶轮顺利安装，叶轮加热温度不能小于243℃。

2）温度上限

在装配的过程中，为保证叶轮内孔的安全性，在温度升高叶轮内径变大的过程中，叶轮内径增大值不能过大，防止叶轮内孔因为变形过大而产生过大热应力，破坏叶轮内孔结构的合理性。叶轮材料许用应力为1 100MPa，为塑性材料，根据第四强度理论，根据公式

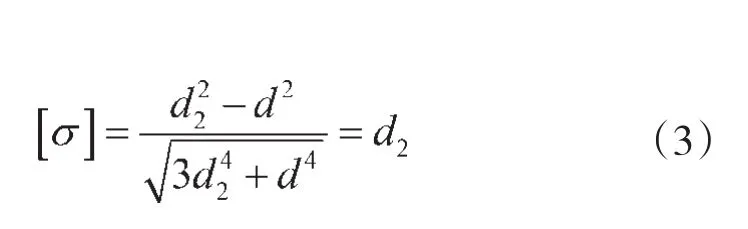
得出叶轮许用应力为：

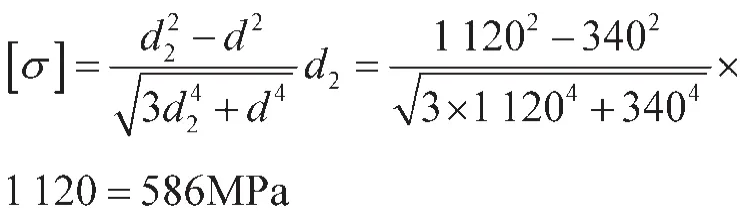
根据公式

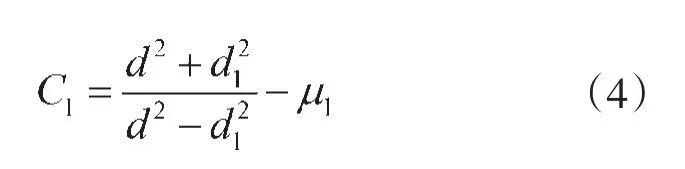
得出轴的刚性系数为：

根据公式

得出孔的刚度系数为：

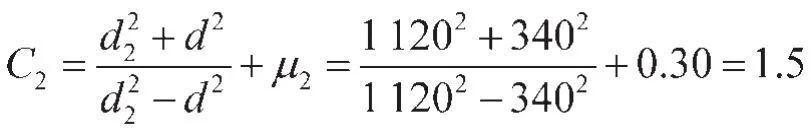
根据公式

式中：E1、E2为轴或孔的材料弹性模量，MPa；C1、C2为轴或孔的材料刚度系数。

得出在该应力下叶轮内孔最大允许热变形为Δmax：

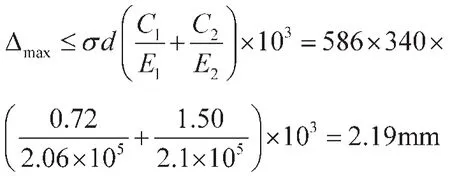
根据公式

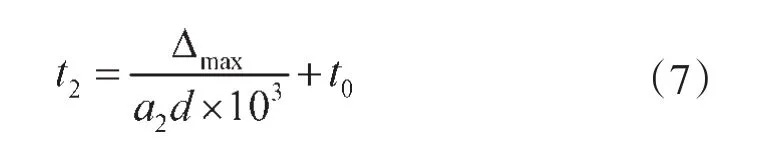
得出叶轮允许加热的最高温度为：

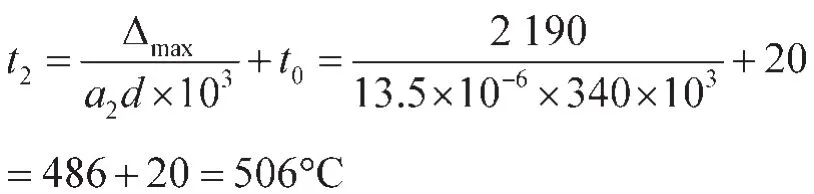
加热温度必须小于506℃。

根据叶轮的安装间隙，公式计算叶轮最低加热温度为243℃；根据叶轮材料性能，公式计算叶轮允许最高加热温度506℃。该叶轮的所需的加热温度必须在叶轮允许的范围内。

2 热载荷下叶轮的变形分析

2.1 建立有限元模型

本文选取闭式三元流叶轮作为分析对象，叶轮内孔尺寸为φ340mm，叶轮和主轴为过盈配合，最大过盈量为0.726mm，叶轮由轮盘、叶片和轮盖组成，叶片焊接在轮盘和轮盖中间，叶轮三维模型如图2所示，叶轮三维网格模型如图3所示。

叶轮材料的密度为7 860kg/m3，泊松比0.3，屈服极限850MPa，强度极限920MPa。不同温度弹性模量、热胀系数、热导率及比热容见表1。

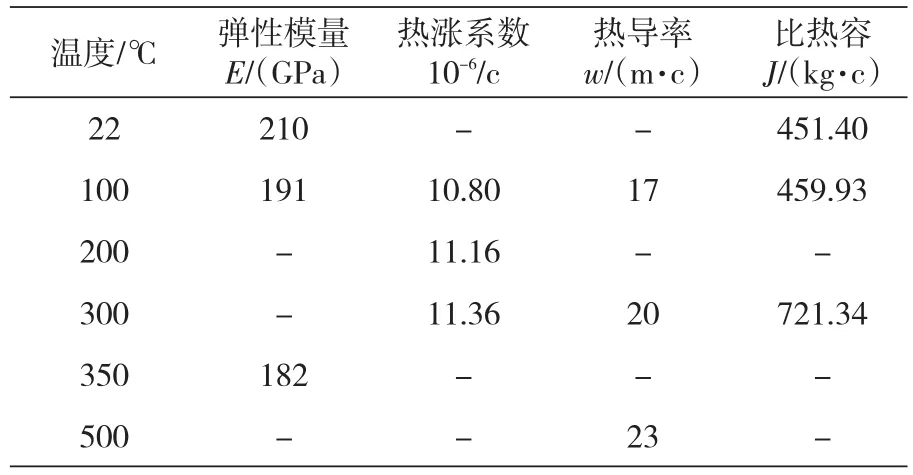
表1 叶轮材料物理性能数据表

2.2 不同温度载荷下叶轮内孔的变形仿真分析

本文采用热-应力耦合场，运用ANSYS WORKBENCH的热分析模块，用顺序耦合方法也称序贯耦合方法来分析叶轮的在热载荷下各变量。首先把计算的温度场作为初始场施加到模型上，然后根据叶轮的温度场计算叶轮在热载荷下的变形。

本仿真热载荷区间为150℃～500℃，温度梯度为50℃。如图4为不同温度载荷下叶轮内孔的变形云图。

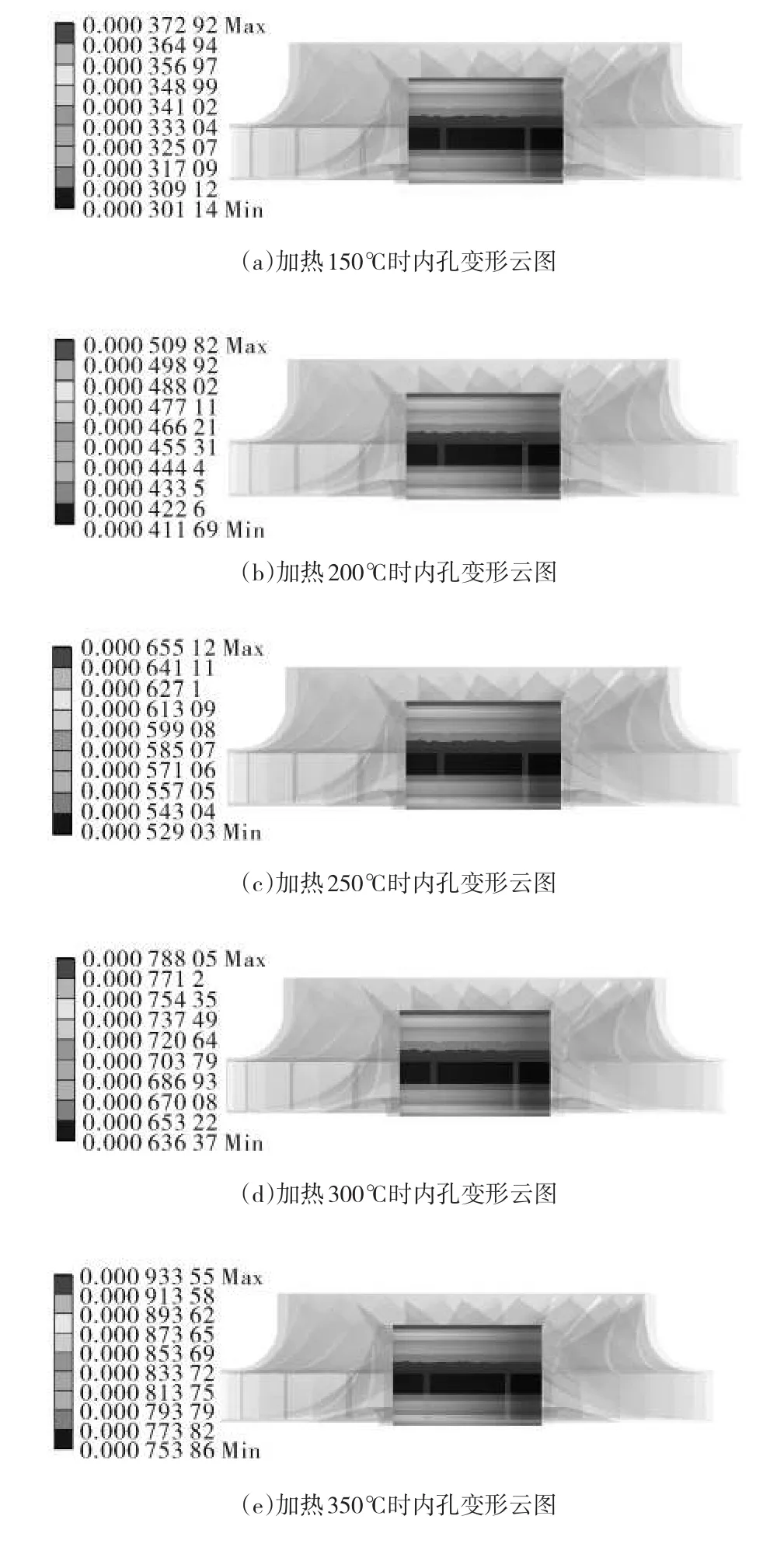
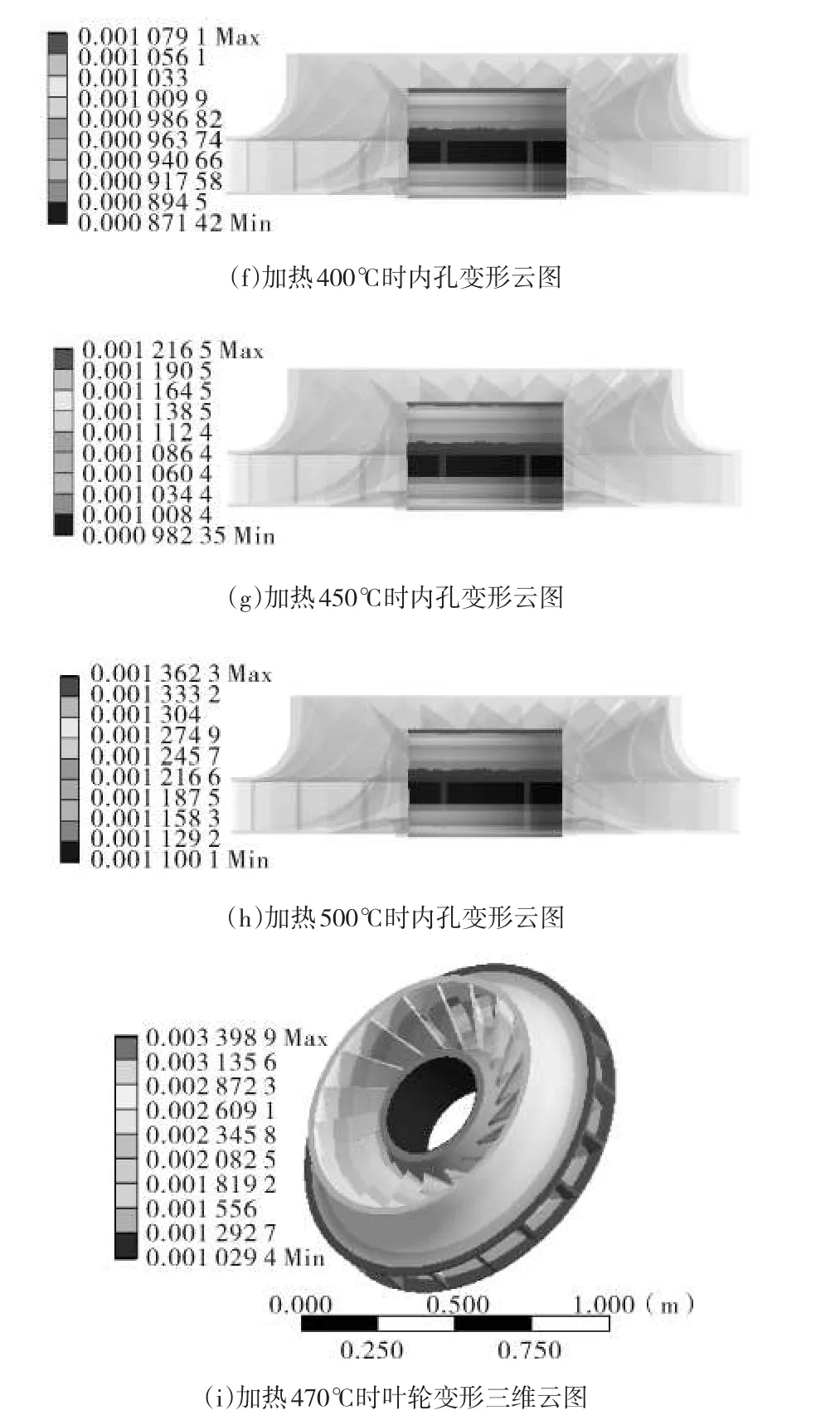
图4 不同加热温度下叶轮内孔变形云图

从叶轮内孔的变形云图可以看出，叶轮内孔增大，且沿轴向变形量由中部向两端逐渐增大。表2列出了不同温度载荷下叶轮内孔的最大变形量与最小变形量。

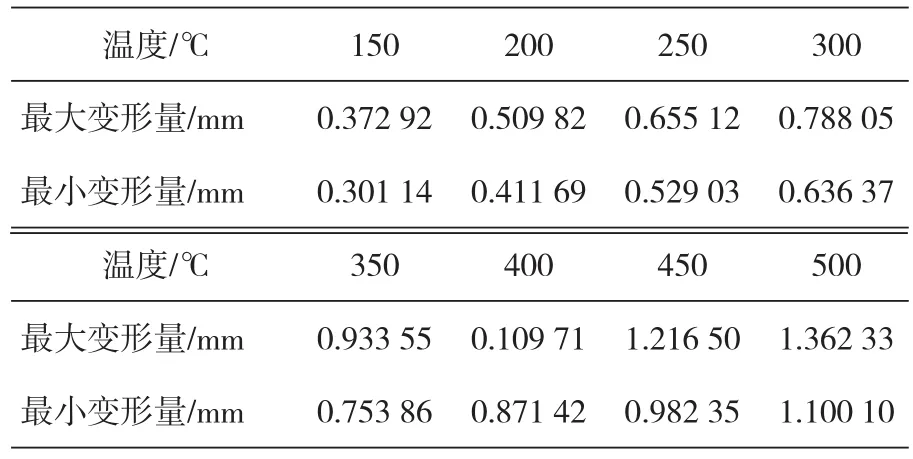
表2 温度与变形值关系

根据表2数据得温度与最小热变形的关系见图5。

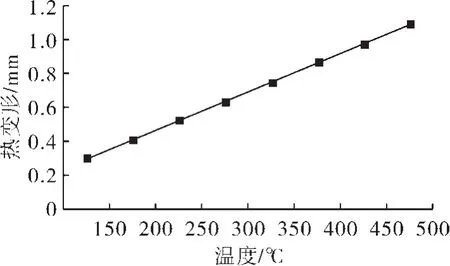
图5 温度与最小变形量的关系图

从图5可以看出，叶轮内孔在不同温度载荷下的最小变形量和温度载荷呈线性变化。

2.3 仿真结果与公式计算值对比分析

在实际生产中，根据零部件材料和零部件配合过盈量及装配间隙值，使用线性膨胀计算公式，计算出工件热装所需的加热温度。该公式为线性膨胀计算公式，未体现热装配接触压强及叶轮与轴之间的摩擦力。

叶轮装配前进行加热，在加热后叶轮内孔直径由D受热膨胀至D+ΔD，那么，变形量有公式（2）：

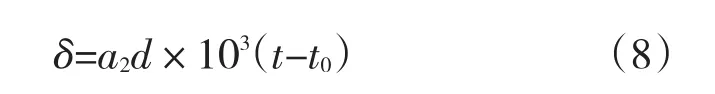
式中：δ为变形量；d为叶轮内孔；a2为线胀系数；t0为环境温度；t为加热温度。

根据线性膨胀公式（2）计算得出不同加热温度下叶轮内孔的变形量列于表3。

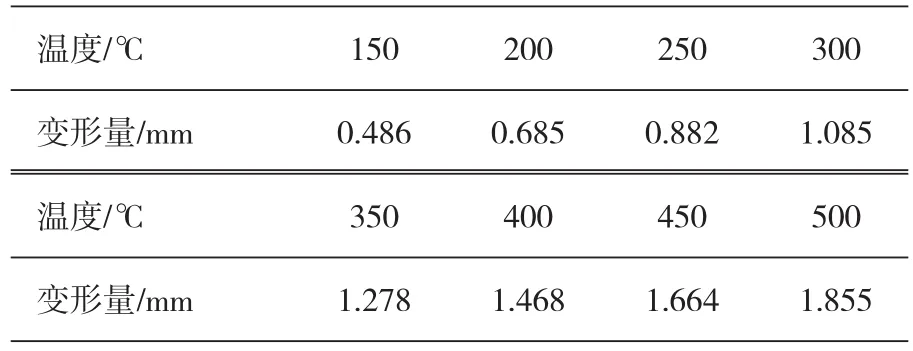
表3 不同加热温度下叶轮内孔的变形量

根据表3数据得温度与最大热变形的关系图6。

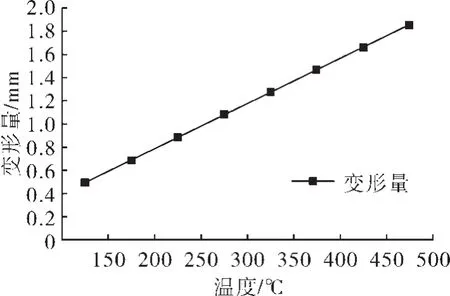
图6 温度与变形量的关系图

3 叶轮热装温度的确定

从图4可以看出，叶轮加热温度和内孔径向变化呈线性变化。当温度为大约在450℃～470℃区间时，叶轮内孔径向最小变形量在1.00mm左右，为了更准确的找出本文研究模型最接近的加热温度，再次仿真分析在460℃和470℃热载荷下叶轮的变形量。仿真实验结果如图7所示：

图7460 ℃和470℃时叶轮内孔变形云图

从图中可以看出，当温度为470℃时，叶轮最小变形量为1.029mm，接近于本文研究模型叶轮的热变形量1.026mm，满足热装要求，所以470℃为模型叶轮所需热装加热的最低温度。为了进一步确认热装温度的合理性，对温度分布进行仿真分析，见图8。

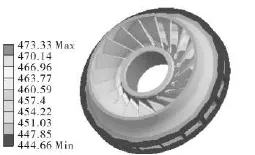
图8 叶轮加热470℃时温度分布云图

从图8中可以发现，温度沿径向变化较大，从内孔处到外圆处逐渐降低；在轴向温度变化较小，叶轮进风口偏大些，整体分布为叶轮外圆处温度最低达444℃，内孔及靠近内孔的进气侧叶片温度最高达473℃。此温度范围均在材料允许加热的温度范围530℃内。

4 结论

本文通过仿真分析，得出在0～500℃内，叶轮内孔变形与加热温度呈线性关系，但其变化率远低于线性公式变化率。说明公式计算简明、直接，但考虑的影响因素不全面，没有考虑叶轮加热变形受结构及轮毂宽度的影响。因此公式计算方式无法精确指导生产。通过对加热温度分布的仿真分析，发现叶轮局部温度接近材料不允许的加热温度，所以类似的叶轮热装时，必须采用均温性好、温度可控的加热方法。在生产中即采用电炉加热，不能采用工程上大都采用的烤枪加热。以防叶轮局部温度过高，对叶轮强度和性能造成不良影响。

[1]刘士学，方先清.透平压缩机强度与振动[M].西安交通大学出版社，1996.

[2]栾其光，郭峰，蔡林邑.离心压缩机转子装配热胀量的计算方法[J].风机技术，2011(6)：44-45.

[3]吴兴伟.联轴器热装时防止轴承退火的措施[J].风机技术，1996(3)：43-46.

■

热装是过盈连接部件的主要安装方式。本文采用有限元仿真分析方法，对过盈连接的叶轮在150℃～500℃范围内的变形分布及变形大小进行仿真分析，得出热装所需的最低加热温度和叶轮加热温度以及变形的关系。并与线性关系进行比较，其变化率远低于线性公式。最后对最低加热温度下，叶轮温度、应力分布及整体变形分布进行仿真分析，对叶轮加热方式提出了要求。

热装；仿真分析；热变形；叶轮

Simulation Analysis on Distortion of CentrifugalImpellersunderThermal Load

Wang Shuixia,Zhang Pu,Zhang Jinna/Xi’an Shaangu Power Co,Ltd

heating assembly;simulation；thermal；impeller

TH452;TK05

A

1006-8155（2015）06-0054-06

10.16492/j.fjjs.2015.06.15009

2015-02-20陕西西安710075

Abstract:Heating Assembly was primary technology of interference connecting parts. In this paper finite element method was applied to simulate and analyze distribution and magnitude of distortion of an impeller under temperature of 150℃～500℃，the lowestheatingtemperatureforthermal assembly was obtained.The variance radio of the relation of impeller heating temperature and distortion which was much lower than the linear-relation.Stress distribution and distortion distribution on the impeller under thistemperatureweresimulatedand analyzed.Atlastrequirementswere presented on heating method of assembly of impellers.