PID参数对动力定位系统定位精度的影响

张嫦利， 王 磊， 李 博， 徐胜文

(上海交通大学 海洋工程国家重点实验室， 上海 200240)



PID参数对动力定位系统定位精度的影响

张嫦利， 王 磊， 李 博， 徐胜文

(上海交通大学 海洋工程国家重点实验室， 上海 200240)

海洋开发促进了动力定位技术在海洋结构物上的应用。动力定位系统能使海洋结构物保持在目标位置和艏向角上。PID控制器在动力定位系统中应用广泛，其参数的选择显著影响动力定位系统的定位精度。为了提高动力定位系统定位精度，借助一个时域模拟软件对PID控制器的参数即比例增益系数Kp、积分增益系数Kd和微分增益系数Ki进行了研究。结果显示,动力定位系统的定位精度受到控制器参数选择的影响。对于研究的动力定位驳船，通过试凑法找到满足定位要求的一组控制参数后，通过控制变量法轻微增加Kp、Kd或Ki会使得定位精度增加。试凑法和控制变量法选取控制器参数的方法将对工程中操作动力定位系统具有一定的参考价值。

动力定位； PID控制； 时域模拟； 定位精度

0 引 言

随着海洋资源需求的激增，诸如钻井、铺管、海洋调查、潜水等海上作业越来越广泛[1]。海洋结构物经常需要保持在目标位置和特定的艏向角上以满足作业要求[2]。现今用于海洋结构物定位的主流方式有锚泊定位、动力定位和锚泊辅助动力定位。其中，动力定位系统最基本的功能是能够借助推进器使浮体保持在特定位置和艏向角上[3]。

动力定位系统主要包括位置测量系统、控制系统、推力系统和动力系统。其中，控制系统接收位置测量系统发出的位置和艏向角等信息，通过由外部环境计算出的扰动力和测得的位置，计算出保持目标位置和艏向角需要的总推力和总力矩，并借助推力分配策略进行分配。目前控制方法有PID控制、H∞鲁棒控制、模糊控制、神经网络控制、遗传算法控制等[4-5]。

PID控制因为控制简单、鲁棒性好，是实际生产中最常用的一种二阶线性控制方法[6]。PID控制方法由PID参数的选择所确定，这对整个动力定位系统产生影响。衡量动力定位系统的标准主要有功率消耗和定位精度。动力定位船舶的定位精度受到PID参数的直接影响[7]。PID控制参数的选择有多种方法，主要有试凑法、经验数据法和扩充临界比例度法[8]。

本文的研究对象是某装有动力定位系统的驳船，主要目的是研究PID参数对动力定位系统定位精度的影响。本文中借助的软件是上海交通大学构建的动力定位试验模拟程序，用试凑法整定出可行的一组参数。一旦发现可行的参数，就可以通过控制变量法进行参数优化。对时域模拟结果进行统计分析，具体分析参数对定位精度的影响，同时给出了参数选择的建议。

1 3自由度运动学和动力学方程

1.1 坐标系定义

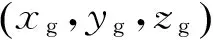
1.2 3自由度运动学方程

动力定位系统一般只考虑水平面3自由度运动，即：纵荡、横荡和艏摇。运动方程为：

(1)

1.3 3自由度动力学方程

由于动力定位系统只考虑浮体的低频运动，因此只需要研究低频运动的方程。低频运动的3自由度运动学方程可写为[9]：

(2)

2 PID控制原理

PID控制器是根据系统的误差，利用比例、积分、微分控制计算得到控制信息的一种控制方法。比例(P)控制的输出量和输入的误差信号成正比关系；积分(I)控制的输出量与输入误差信号的积分成正比关系；微分(D)控制中，控制器的输出和输入信号的微分成正比关系[10-11]。

动力定位系统的控制系统要实现滤波和反馈控制两大功能。动力定位系统不考虑高频运动，因此需要滤去位置测量系统测到的高频信号和噪声。控制系统还需要计算出所需的总推力和力矩，并分配给各个推进器。这里的总推力和力矩指的是抵制横荡、纵荡的力和抵制艏摇的力矩。PID控制器的目标是通过只补偿观测器估算的低频运动，使得海洋结构物保持在特定的位置和艏向角上[12]。

本文借助的时域模拟程序是在Simulink平台上建模。具体包括位置设定模块、控制系统模块、推力系统模块、波浪载荷模块、动力学方程模块和状态观测器模块[9]。控制系统模块中选择了PID 控制算法和Kalman滤波，使得控制系统形成了位置信息的后反馈系统加上风前馈系统。

动力定位系统的PID控制方法如下式所示[13]：

(3)

(4)

(5)

式中:Kp、Ki、Kd分别是比例、积分和微分增益系数;Δx、Δy、Δψ分别是大地坐标系中x、y方向和艏向上实际位置和目标位置的偏差;Tx、Ty、Mψ分别是控制系统计算出的x、y方向的推力和艏向的力矩;TWfx、TWfy、TWfψ分别是风前馈在x、y方向的力和艏向上的力矩。比例增益系数的作用是提供与位置偏差成比例的回复力；积分增益系数能够抵消缓慢变化和静态的平均力，微分增益系数提供的是阻尼力。

PID控制器的工作原理如图2所示[14]。

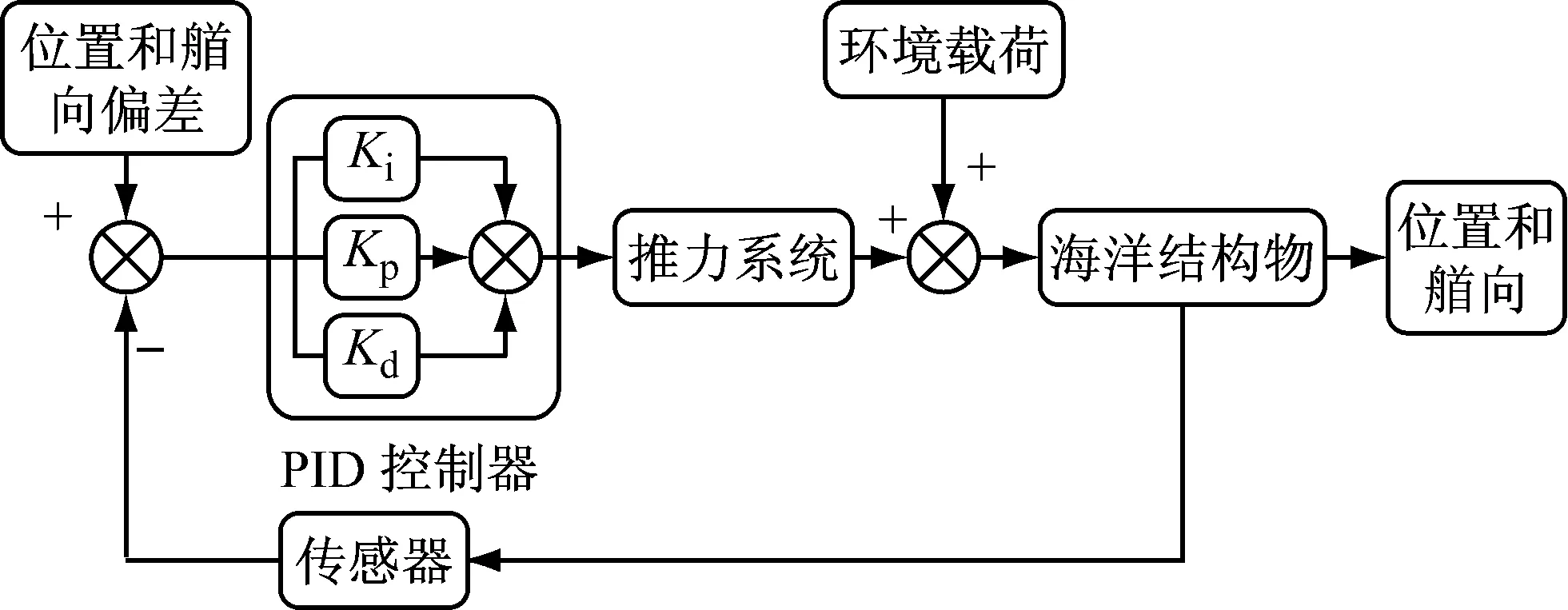
3 数学模型

3.1 驳船参数

本文的研究对象是装有动力定位系统的驳船，三维模型如图3所示。

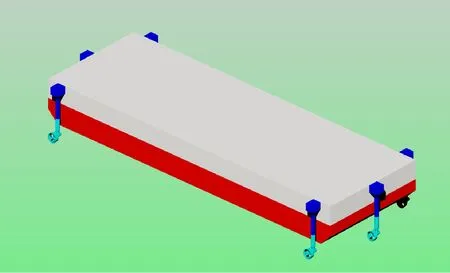
图3 装有动力定位系统的驳船的三维模型

驳船的主要尺度如下：长度LPP=150.00 m，宽度B=50.00 m,吃水T=10.00 m,重心高度(距基线)KG=10.00 m,排水量V=73 750 m3,横摇惯性半径Kxx=20.00 m,纵摇惯性半径Kyy=39.00 m,艏摇惯性半径Kzz=39.00 m。

此外，驳船采用6个全方位螺旋桨，螺旋桨直径3.6 m，最大推力800 kN。具体布置如图3所示。

3.2 海洋环境载荷

本文未考虑风载荷作用，由于此种情况下浪、流同向作用时为最恶劣的环境条件，故取浪、流同向作用作为计算的环境条件，其具体参数:环境力方向180°,有义波高HS=5.27 m,谱峰周期TP=13.4 s,谱峰因子γ=3.3,波浪谱Jonswap,流速VC=1 m/s-1。数值模拟中，环境载荷方向取180°，即在大地坐标系中沿着x轴的负方向。

4 PID控制器参数的整定

应用经典的试凑法对PID的参数进行反复调整，直至找到满足定位要求的一组参数。动力定位船舶允许的位移是水深2%～4%[15]。驳船实际水深超过100 m。因此可取参数应保证驳船的位移在2～4 m。

设定目标艏向角30°，应用时域模拟程序对每组选定参数进行12 600 s的数值模拟，通过定位精度看参数是否可取。通过试凑法，发现Kp= 0.001 5、Kd= 0.06、Ki= 1×10-5这组参数满足要求[9]。这组参数下，纵荡、横荡、平均偏移半径、艏摇的标准差分别是1.242、 0.619 2、1.387 8 m和0.968 5°。驳船的定位表现如图4和图5所示。在进行数据分析时，去除了首尾各1 800 s以保证数据的稳定性。

图4 纵荡和横荡的时历曲线

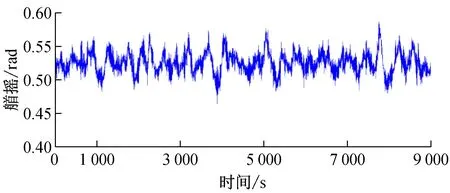
图5 艏摇的时历曲线

5 数值模拟与分析

5.1 数值模拟

本文借助上海交通大学编写的时域模拟程序，驳船的目标艏向角ψsy有30°和60°。

数值模拟的目的是比较不同参数下驳船定位效果。计算得到驳船的纵荡、横荡、平均偏移半径、艏摇的标准差。更高的定位精度代表着更优的定位性能，即将海洋结构物保持在目标位置和艏向上的能力。本文应用上述程序对每个情况进行12 600 s的数值模拟。

数值模拟中使用的PID参数如表1所示。用试凑法整定出可行参数后，运用控制变量法进行参数优化。对于每个目标艏向角，每次只改变Kp,Kd和Ki中的1个。对于每个参数选定3组数，因此每个艏向角对应9组参数。

5.2 计算结果和分析

对每组参数下的驳船进行数值模拟，直接得到位移(纵荡、横荡、艏摇)的时历。通过统计计算得到位移(纵荡、横荡、平均偏移半径、艏摇)的标准差，如表2所示。

从表2可以看出，当Kp,Kd和Ki中有任一个微量增加时，驳船的位移减少。这种现象对Kp最明显。对每个参数以最小值为参照点，通过比较增量的百分比来研究。可以看出，在目标艏向角为30°时，当Kp增加时横荡的减小值达到19.65%；在目标艏向角为60°时，当Kp增加时横荡的减小值达到18.64%，平均偏移半径在动力定位的定位精度中权重较大；当目标艏向角为30°时，分别微增Kp,Kd和Ki，平均偏移半径的减小量分别达到12% , 5.7% 和 3.4%。对于目标艏向角60°来说，相应的值是15.3% , 3.2%和3.0%。位移的趋势图如图6～8所示。

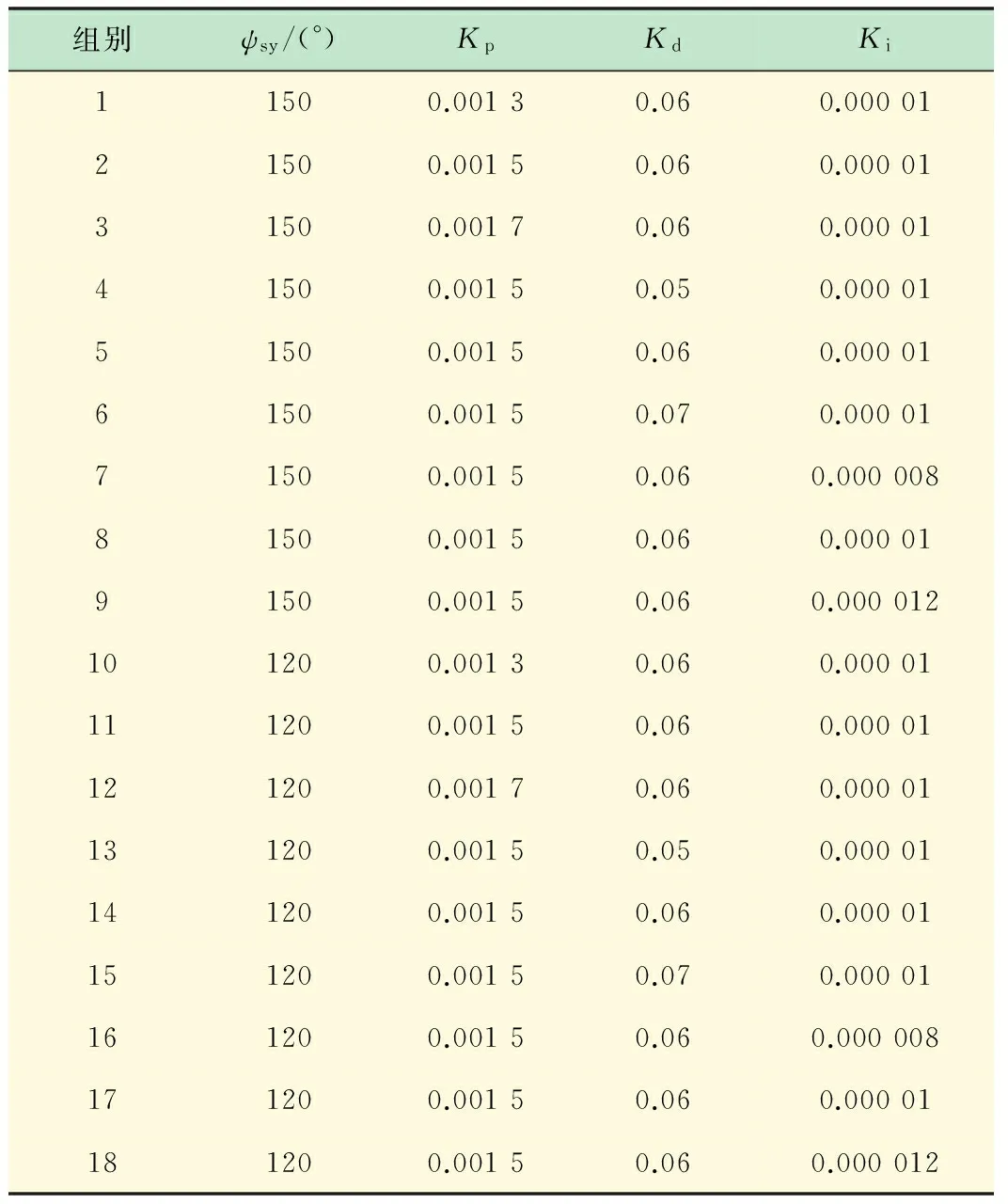
表1 数值模拟中控制器选择的PID参数

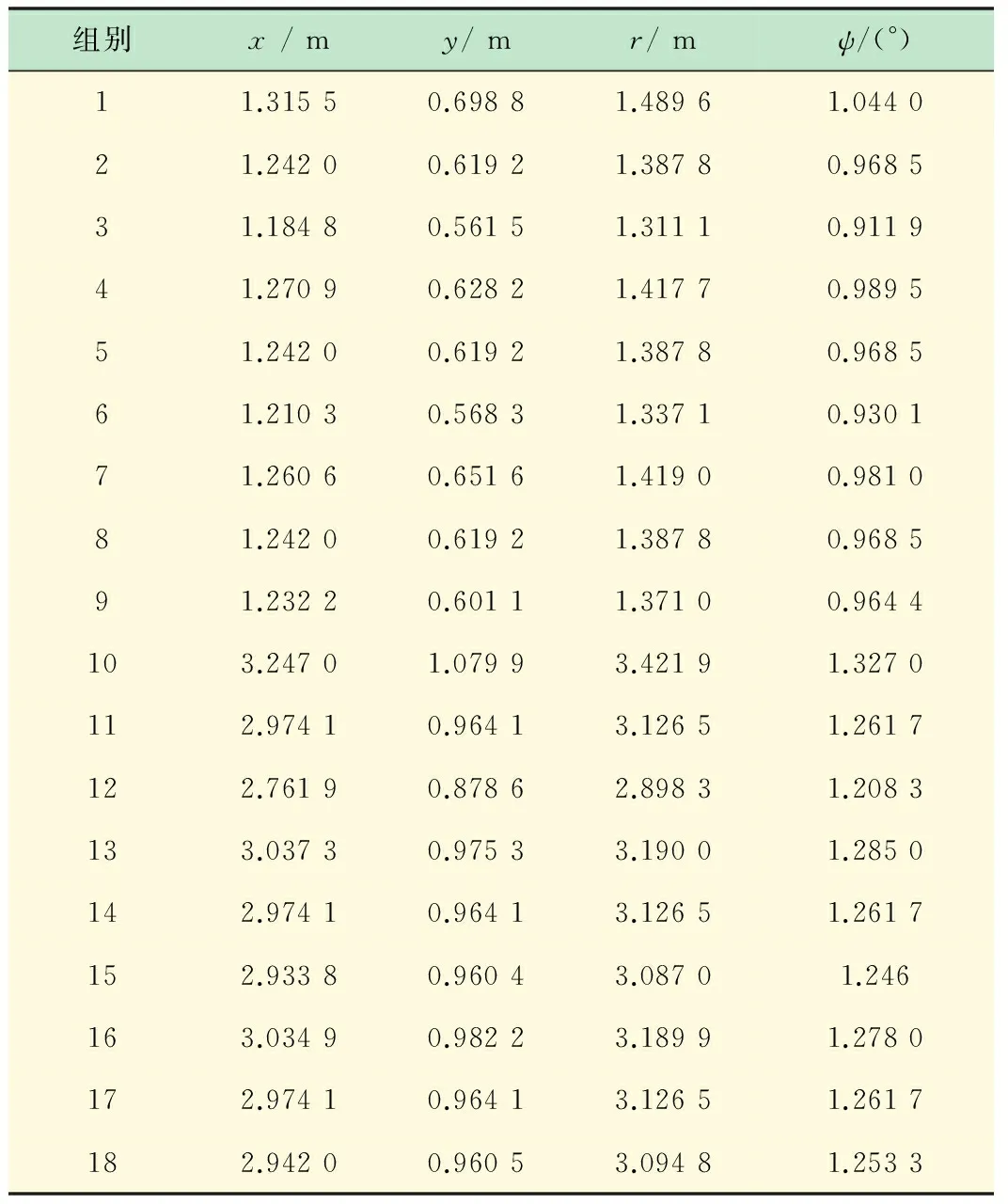
表2 位移的标准差

图6 Kp的变化对位移的影响

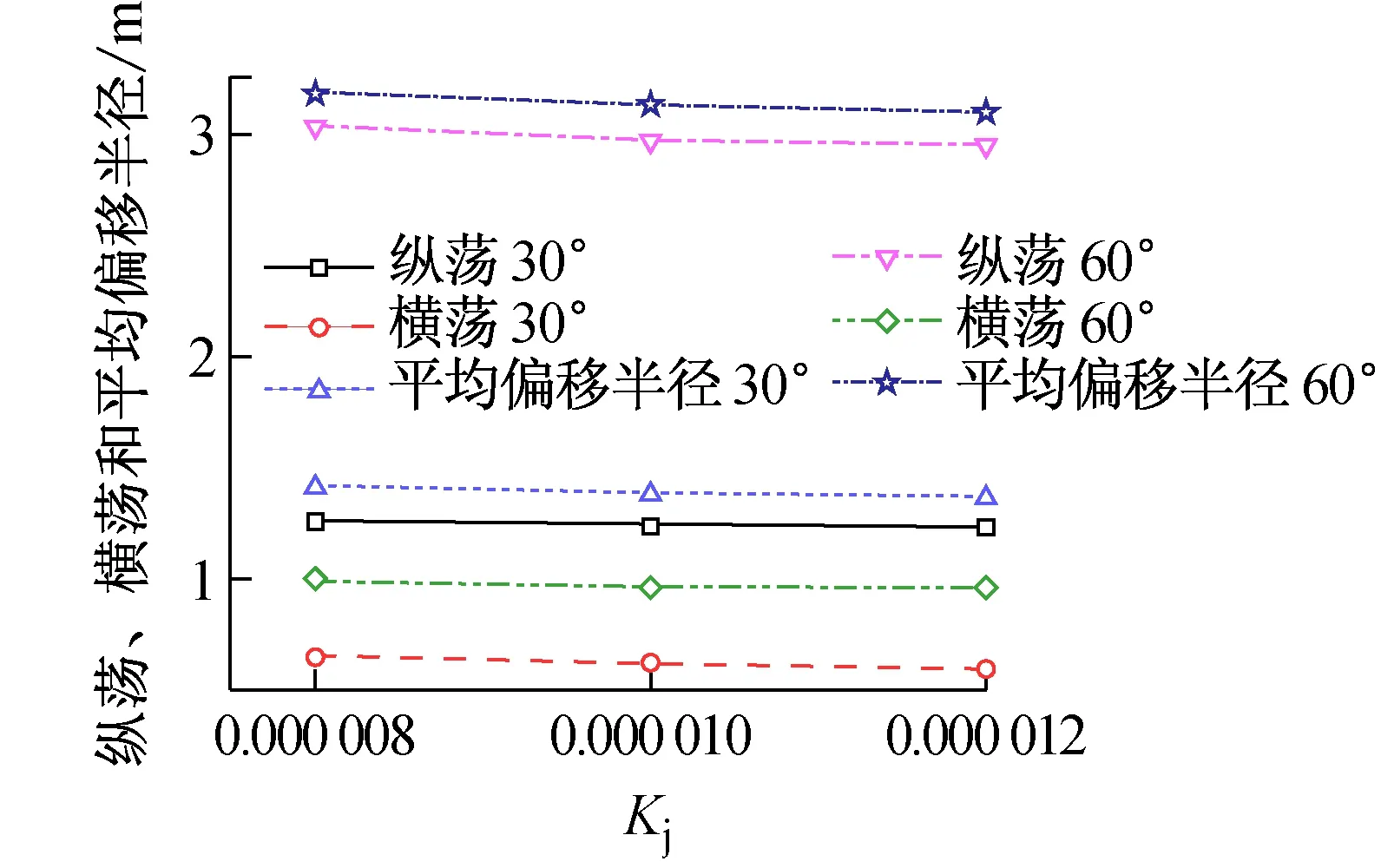
图7 Ki的变化对位移的影响

(1) 由图6可以看到,给验证可行的比例系数Kp增加或减少一个微量值，定位精度有明显变化。具体表现在，微量减小Kp会增大驳船的位移，微量增大Kp会减小驳船的位移。从PID控制原理上来说，一般情况下，增大Kp会加快系统的反应速度，对减小静差有利[12]。静差是控制系统准确性的重要指标，指的是被控制量的稳定值和给定值的差。在动力定位系统中，增大Kp有利于减小位置和艏向角的静差，即位移。需要注意的是，这样的趋势只在一定范围内成立，因为过大的比例系数会使系统产生较大的超调和振荡，从而使稳定性变差。

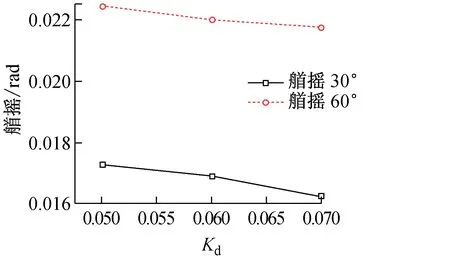
图8 Kd的变化对位移的影响

(2) 由图7和图8可以发现，给验证可行的Ki和Kd增加或减少一个微量值，定位精度有变化，变化程度没有改变Kp引起的大。具体表现在，微量减小Ki或Kd会增大驳船的位移，微量增大Ki或Kd会减小驳船的位移。一般情况下，增大Ki会加大积分作用，有利于增大稳定性，但会增大超调。增大Kd能加快系统响应，减小超调、增大稳定性，但会降低系统抗干扰的能力。因此，Ki和Kd对定位精度的有利影响趋势也是在一定范围内成立的。

(3) 由表2和图6～8可知，改变Kp、Kd和Ki对横荡的影响最明显。在目标艏向角30°时，分别增大Kp、Kd和Ki，横荡的减小量达到19.65%，9.54%和7.75%。在目标艏向角为60°时，分别增大Kp、Kd和Ki，横荡的减小量达到18.64%，1.53%和2.21%。这与推进器的布置方式有关。

6 结 论

分析了PID参数对某动力定位驳船的定位精度的影响，并提出了相关建议，得到了以下结论：

(1) 分别增大比例系数Kp、 微分系数Kd和积分系数Ki都能减小位移，提高驳船的定位精度。这个结论在一定范围内保持成立。因此，在工程实际或模型

试验中，通过试凑法得到满足定位要求的一组参数后，即可微量增大某一PID控制系数来优化定位效果。

(2) 一定范围内，增大比例系数Kp对改善动力定位系统的定位精度效果最为明显。

(3) 本文研究的驳船的横荡受到PID参数的影响最大。工程实际或模型试验中，对于具有相似布置方式的推进器的船舶，可以借鉴相关参考。

(4) 本文只采用了控制变量法对PID参数进行优化，工程实际中可以考虑同时增大PID参数来尝试获得更高的定位精度。

[1] Jorrit-Jan Serraris.Time domain analysis for DP simulations[C]∥AE, Hawaii,2009.

[2] 杨 欢，王 磊，李 欣.锚泊辅助动力定位研究与进展[J].实验室研究与探索,2012,31(4):88-92.

[3] Asgeir J Soresen. A survey of dynamic positioning control systems[J]. Annual Reviews in Control, 2011,35:123-136.

[4] 赵之韵.船舶动力定位系统控制器设计[D].大连：大连海事大学,2009.

[5] 邹 刚.基于PID 控制的锚泊辅助动力定位系统研究[D].上海：上海交通大学,2014.

[6] 阿依布·阿布都拉，王彩霞.PID控制在冶金和热处理中的应用[J].Hot Working Technology, 2013，42(6): 226-229.

[7] Xu Shengwen, Wang Xuefeng, Wang Lei,etal. Dynamic positioning with roll-pitch motion control for a semi-submersible[C]∥OPE, Alaska, 2013:973 -978.

[8] 金 奇，邓志杰.PID控制原理及参数整定方法[J].重庆工学院学报,2008,22(5):91-95.

[9] 李 博.动力定位系统的环境力前馈研究[D].上海：上海交通大学,2013.

[10] 邹 刚，王 磊，刘翰林. 锚泊辅助动力定位系统艏向控制模式研究[J].海洋工程，2013,31(5):11-17.

[11] 杨巨庆，黄 健，段丽华. PID控制技术与应用[J]. 哈尔滨师范大学自然科学学报，2004,20(2)：76-79.

[12] Dong T Nguyen, Asgeir J Sønsen. Set point chasing for thruster-assisted position mooring[J]. IEEE Journal of Oceanic Engineering, 2009, 34:548-558.

[13] 刘翰林.旁靠多浮体动力定位系统数值模拟与研究[D] .上海：上海交通大学,2013.

[14] 周 利.半潜式钻井平台动力定位推力系统理论设计及模型试验研究[D] .上海：上海交通大学,2009.

[15] Wang Lei, Sun Pan, Wang Liang. Research on time domain simulation of dynamic positioning for a deep water semi-submersible platform[J].Scientia Sinica Phys, Mech & Astron,2011, 41(2) :123-131.

Effects of Selection of PID Coefficients on Positioning Accuracy of DP System

ZHANGChang-li,WANGLei,LIBo,XUSheng-wen

(State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China)

Offshore exploration has promoted the development of dynamically positioned (DP) marine structures. With dynamic positioning system, ocean constructions can be kept at a desired position and heading. PID controller is widely used in the DP system (DPS). Furthermore, the positioning ability is essentially affected by the selection of PID coefficients. To enhance the positioning accuracy, the influence of the parameters of PID control, which include proportional gain, derivative gain and integral gain are investigated by a dynamic positioning simulation program. The obtained results indicate that the positioning accuracy is influenced strongly by these coefficients. As for the studied barge, a set of parameters is obtained by trial-and-error method, the positioning accuracy of the DPS increases as increasingKp,KiorKdslightly using control variable method. Additionally, a guidance that combines trial-and-error method and control variable method on the selection of the coefficients is given, the method may be useful for the operator of DPS.

dynamic positioning; PID control; time domain simulation; positioning accuracy

2014-05-07

国家自然科学基金项目(51179103)

张嫦利(1989-)，女，江苏南通人，硕士生，主要从事动力定位研究。Tel.:18818212284; E-mail：zhangchangli@sjtu.edu.cn

王 磊(1971-)，男，安徽蚌埠人，副教授，主要从事动力定位系统的研究。Tel.:021-62932025; E-mail：wanglei@sjtu.edu.cn

P 751

A

1006-7167(2015)03-0008-05