基于粒子滤波的多枚声呐浮标联合跟踪定位算法

陈增增 马晓民 陶伟(第七一五研究所，杭州，310023)



基于粒子滤波的多枚声呐浮标联合跟踪定位算法

陈增增 马晓民 陶伟
(第七一五研究所，杭州，310023)

摘要由于被动声呐浮标目标测量源的不确定性以及位置解算方程的非线性，声呐浮标联合跟踪定位面临着非线性非高斯问题，提出一种基于粒子滤波的多枚声呐浮标联合跟踪定位算法。该算法将最优贝叶斯滤波与蒙特卡洛随机采样方法相结合，在更广义的条件下实现了目标最优状态估计。算法仿真结果表明，可以较大程度的提高目标位置估计精度。

关键词联合定位；粒子滤波；蒙特卡洛积分；重要性采样

在复杂的海洋信道中，被动声呐浮标的目标检测过程存在着测量源的不确定性，即在一次处理中目标方向可能没有信号凸起，信号凸起的方向也可能与真实的目标方向存在误差，使得被动声呐浮标联合定位困难或者定位误差大，甚至无法为武器使用提供有效的目标指示。

利用最优估计理论而发展起来的跟踪定位方法可以有效的提高定位精度并克服失序观测困难。本文重点研究并提出了一种基于粒子滤波的多枚声呐浮标联合跟踪定位算法。通常，目标跟踪定位的目的是在离散的时间序列中，“找出”感兴趣的目标。而目标可由其自身状态描述，于是跟踪定位问题等价于目标状态的求解问题，这个求解过程可以用估计理论来实现。进一步，状态估计需要基于一定的观测数据和目标先验信息，构造贝叶斯概率模型，问题的实质转换为求解表征目标状态的后验概率。粒子滤波（particle filter）[1-2]即是求解贝叶斯后延概率的一种实用算法。所谓粒子，是形容尺度极小的滤波器，可认为是一个代表了目标状态中的一个点；所谓滤波，是指可以“滤出”目标的当前状态，在估计理论中也指由当前和以前的观测值来估计目标当前状态。

1　算法原理

粒子滤波是贝叶斯最优滤波与Monte Carlo随机采样方法相结合的一种滤波算法[3]。其突出优点是不受线性高斯假设的限制。

1.1非线性贝叶斯跟踪建模

跟踪问题的实质是获取目标状态，本文首先构建非线性贝叶斯跟踪框架，建立目标运动和多枚浮标被动声呐浮标观测方程，然后采用粒子滤波进行求解。

以{xk, k∈ N }表示目标状态序列，考虑状态方程为如下形式的跟踪问题：

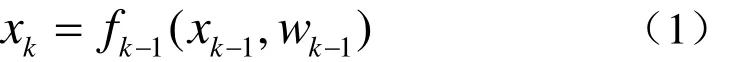
其中f: Rn x×Rnw→Rnx表示状态x的非线性函k−1数，R表示实数域，{wk−1,k∈ N}为独立同分布的过程噪声序列，nx和nw分别表示和过程噪声矢量的维数，N是自然数集合。跟踪的目标就是依据观测数据递归估计状态xk，观测zk由观测方程与之联系，如下表示：

其中h: Rn x×Rnv→Rnz是非线性函数，{vk, k∈ N }为独立同分布的观测噪声序列，nx和nv分别表示观测和观测噪声矢量的维数，以Zk表示直到时刻k的观测集合Zk={ z1, z2, L, zk}。

本文给出递推贝叶斯滤波公式[4]：

假设在k−1时刻已经获得了p(xk−1|Zk − 1)，那么根据状态的一阶Markov特性，状态一步预测的概率密度函数为

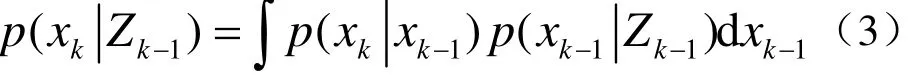
其中p(xk|xk−1)表示状态转移概率密度，在加性过程噪声系统中：

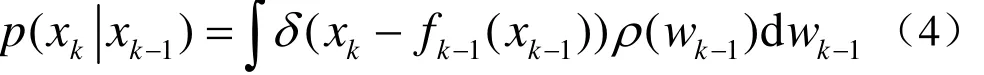
式中，δ(⋅)为Dirac delta 函数。

在已经获得p(xk|Zk−1)基础上，计算一步预测概率密度函数为

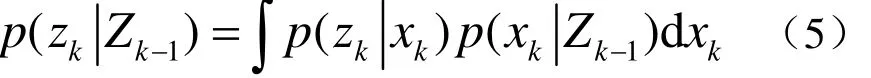
其中，p(zk|xk)表示输出似然概率密度函数，在加性量测噪声系统中：

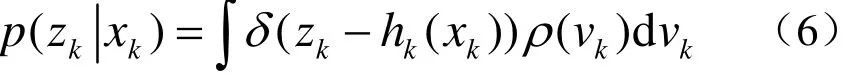
在k时刻已经获得新的量测信息zk，可以利用贝叶斯公式计算得到系统状态的后验概率密度函数

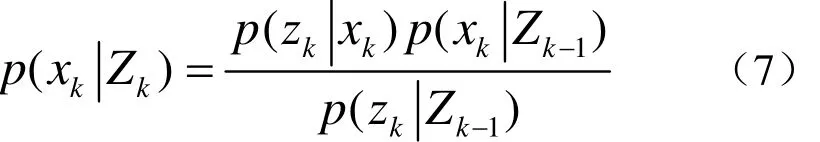
由式(5)可知，式(7)右侧分母部分为归一化常数。式(4)和式(6)是非线性贝叶斯建模的关键。

于是，k时刻的状态估计及其估计误差协方差阵为：

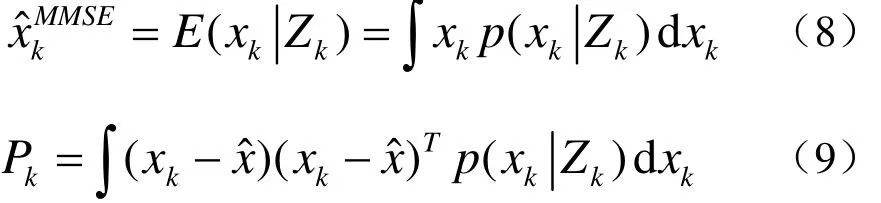
最优贝叶斯滤波为非线性最优滤波提供了一个一般的理论框架，实际中因其需要无尽的参数及大量的运算而应用起来十分困难。粒子滤波可以通过计算机数值运算方法获得贝叶斯滤波的近似解。

1.2蒙特卡罗积分

Monte Carlo积分方法[5]能够真实地模拟任意物理过程，并取得满意的精度，其基本思想是：通过抓住事物运动的几何数量和几何特征，利用数学方法来加以模拟建立一个概率模型或随机过程，并使其所求参数等于问题的解，然后通过对模型或过程的观察或抽样试验计算所求参数的统计特征，最后给出所求解的近似值，解的精确度可用估计值的标准误差来表示。

设x∈ Rn为n维空间向量，计算如下数值积分

蒙特卡罗积分就是将积分值看成是某种随机变量的数学期望，并用采样方法加以估计，可以考虑将被积函数f(x)做如下分解

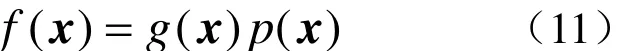
其中，p(x)为状态变量x的概率密度函数，满足p(x)≥ 0且

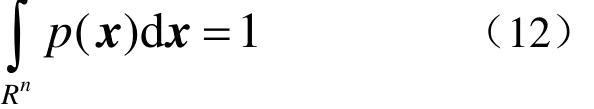
同时，I可以看成是g(x)的数学期望，即I= E[ g (x)]。

假设π(x)可产生独立同分布样本{xi,i= 1,2, L ,N }，则对积分

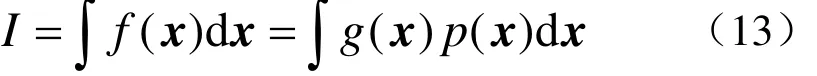
的估计就可用如下样本平均法

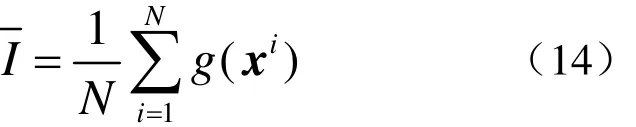
如果所有的xi都是独立的，那么是I的渐进无偏估计，即将几乎处处收敛到I。

1.3序贯重要性采样

递推贝叶斯滤波给出了计算后验密度函数p(xk|Zk)的递推公式，其中量测信息。但是，的计算包含了复杂的概率密度函数积分运算问题，即使假设噪声和状态为高斯分布的情况下，概率密度函数的积分运算也是非常困难的。在非线性非高斯条件下，计算更是根本无法实现的。为了应对上述复杂的积分运算，通常使用前面所介绍的随机采样运算的蒙特卡罗法将复杂的积分转化为离散样本加权和的形式来进行状态估计。

SIS方法针对难以直接从后验概率密度函数中采样的问题，而寻找一个容易进行采样（已知概率分布）的概率密度函数，即重要性密度函数，实施重要性采样。那么，对于k时刻的函数状态估计问题可进行如下变形

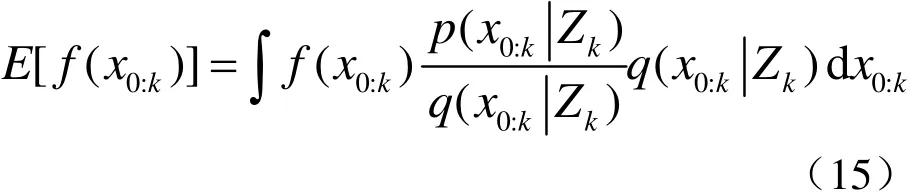
对p(x0:k|Zk)应用贝叶斯公式得

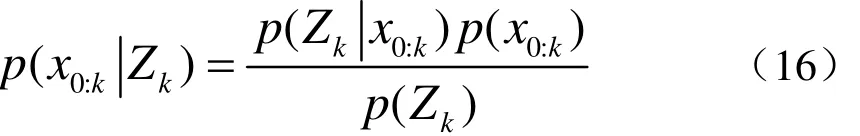
假设w0:k为已知的非归一化重要性权值，其表达如下

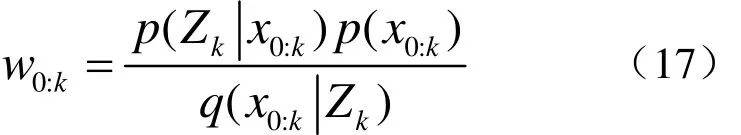
对(15)式整理得

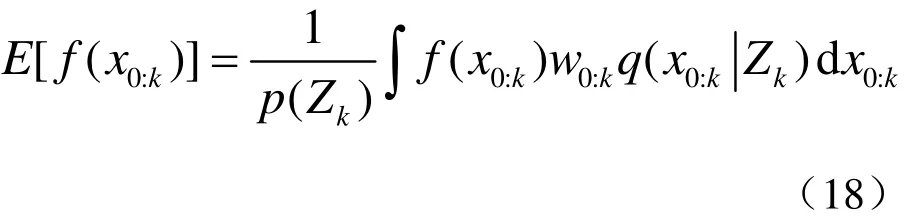
式中

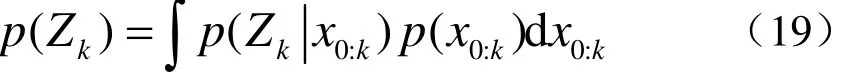
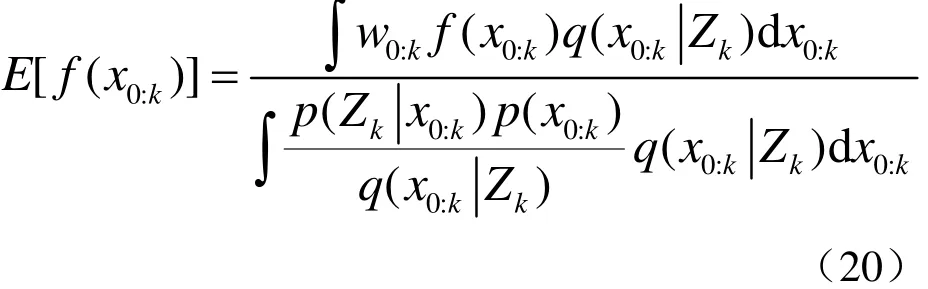
再将w0:k代入后得到

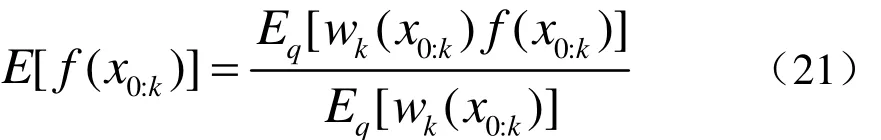
应用蒙特卡罗方法可将上式近似变换为

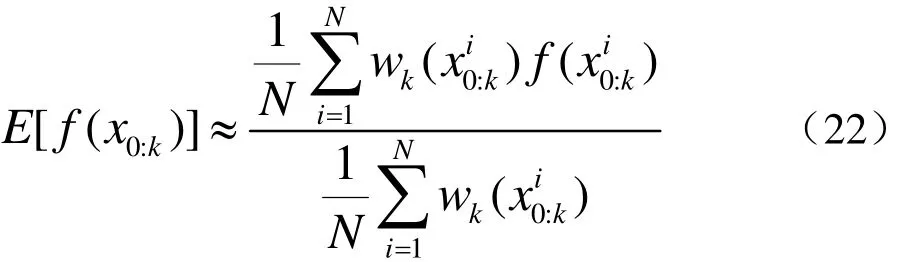
化简后得到

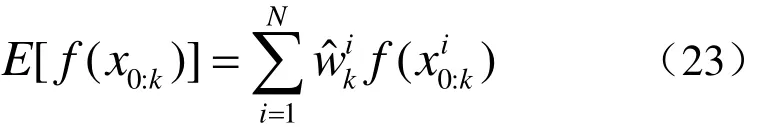
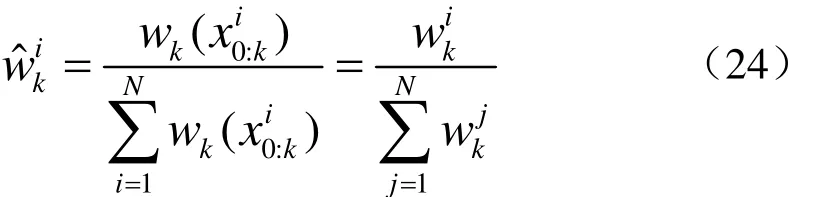
为了计算k时刻的真实概率分布，而又不希望改动先前时刻的状态，所以选择重要性概率密

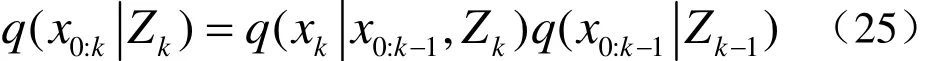
这里假设当前时刻的状态值独立于下一时刻的量测值，同时假设状态向量符合Markov过程，即量测值与状态相互独立，那么可以得到

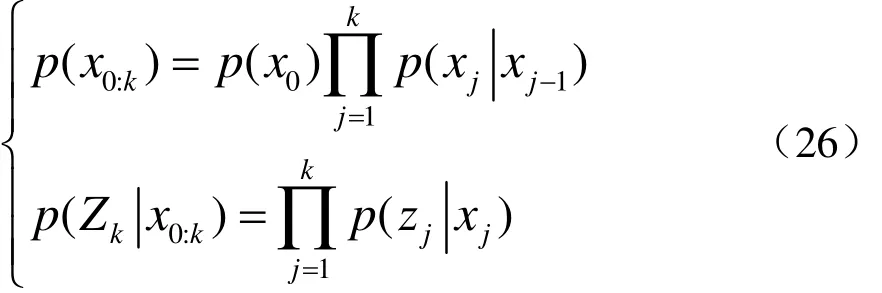
将式(25)代入式(17)，容易得出有关每个粒子权重wk的递推公式

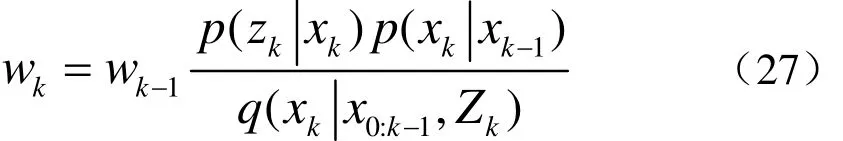
在SIS方法中，选取的重要性概率密度函数要能按照式(22)进行分解，那么重要性权值的方差必然会随时间增大而增大，原理如下

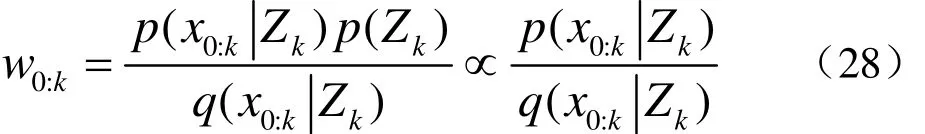
上式被称为“重要性比值”，通过它可以证明方差随时间积累。

重要性权值的方差会随时间增大而增大，那么必然会导致SIS方法的退化现象。其表现是：经过若干次迭代后，除了少数粒子外，其余粒子的权值均可忽略不计，从而使得大量递推浪费在几乎不起作用的粒子的更新上，甚至最后只剩下一个权值为1的有效粒子，而其他粒子的权值为零，这意味着大量计算浪费在那些权值极小的粒子上，这些粒子不但降低了状态估计的精度，而且对逼近的贡献几乎为零。

为后续论述方便，定义有效粒子容量为

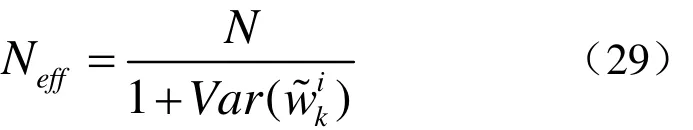
显然，退化问题在粒子滤波中是一个不期望的影响作用，减少这种作用的最好方法就是采用非常大的样本容量N，然而在许多情况下无限扩大样本容量是不现实的，所以需要采用其他方法来降低退化现象带来的负面影响。

1.4重采样

重采样的目的在于减少权值较少的粒子数目，而把注意力集中在大权值的粒子上，即增加权值大的粒子数目。当前，有多项式重采样、残差重采样、最小方差重采样、系统重采样等方法。不同的重采样方法对估计精度的影响也不尽相同，其基本原理是：一旦发生了退化现象，便在原来重要性采样的基础上引入重采样，淘汰权值低的粒子，集中权值高的粒子，从而抑制退化现象。

由式(29)可知，1≤Neff≤ N，当所有的权值=1/ N (i=1,2, L,N)时，N= N；当只有eff一个权值，而其余权值(i=1,2,L ,N , i≠ j )，N=1。可见，Neff eff越小退化现象越严重，那么对于退化现象可由Neff的大小判断。

重采样可以减少退化现象，其目的在于增多权值较大的粒子数目。重采样的基本过程是通过对后验概率密度的离散近似表示，再进行N次采样，产生新的粒子集

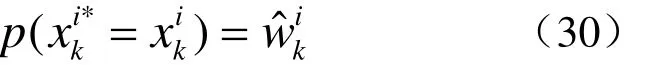
2　算法设计

本文在标准SIS方法中引入重采样步骤，设计了适合多枚声呐浮标联合跟踪定位的序贯重要性重采样（SIR）算法。该算法步骤如下：

Step1：初始化（k =0）

从先验分布p(x0)中采样N个样本，

Step2：重要性采样，i=1,2, L ,N

②计算重要度权值

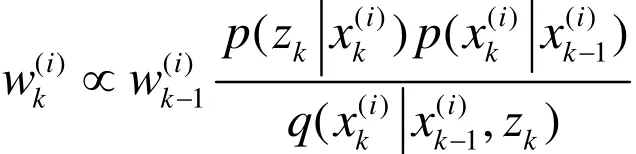
Step3：判定是否重采样

②计算重要度权值

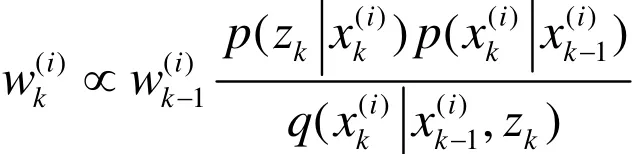
④判定是否重采样

Step5：输出

Step6：令k= k +1，当下一时刻量测值到来时，返回Step2。

3　算法仿真

为验证本文所提算法的处理效果，对双被动声呐浮标联合定位进行数据模拟，并利用SIR算法实施跟踪滤波。声呐浮标与目标态势如图1，声呐浮标以RECEIVE标识，θ1、θ2为测量的目标方向角，仿真取测向误差σθ=5°，目标以5 m/s沿正横轴方向做匀速直线运动。

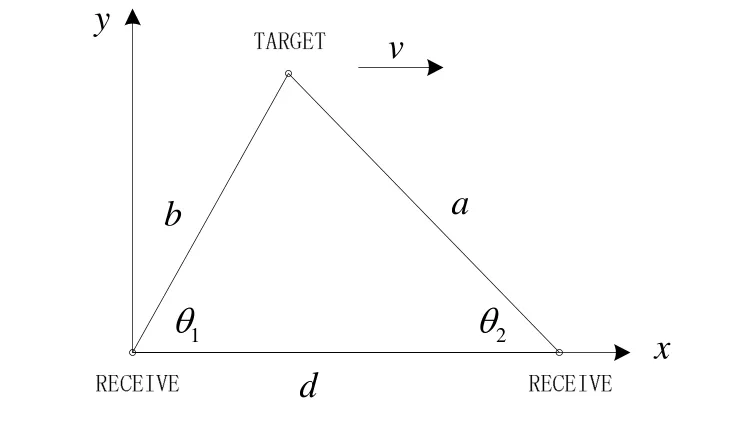
图1　探测态势

在图1态势下，联合定位解算方程如下：

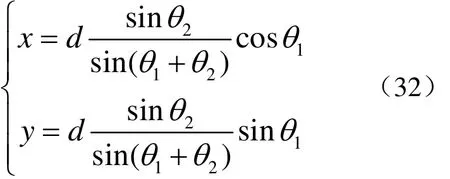
根据测向误差，经非线性传递并利用计算机数值方法解算的双声呐联合定位误差椭圆如图2，其中纵向误差较大而横向误差相对较小。

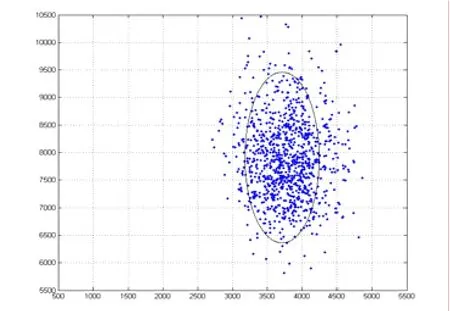
图2　定位误差椭圆

图3为算法处理结果，实线为粒子滤波处理结果，虚线表示卡尔曼滤波处理结果。图中虚线表示联合定位的测量值，实线为SIR算法处理结果。可以看出，跟踪定位处理大大提高了目标的位置估计精度，对比卡尔曼滤波的精度，也有较大提高。

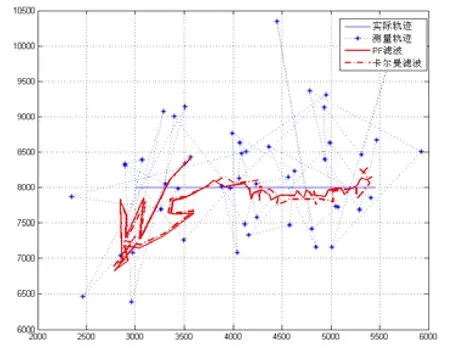
图3　跟踪滤波结果

图4为算法经100次蒙特卡洛仿真的平均均方根误差值，可见收敛速度较快。图5为测量误差不变、设置的浮标数增加到三个时对机动目标跟踪的结果图，相较于现在使用的几何定位方法，有显著提升。

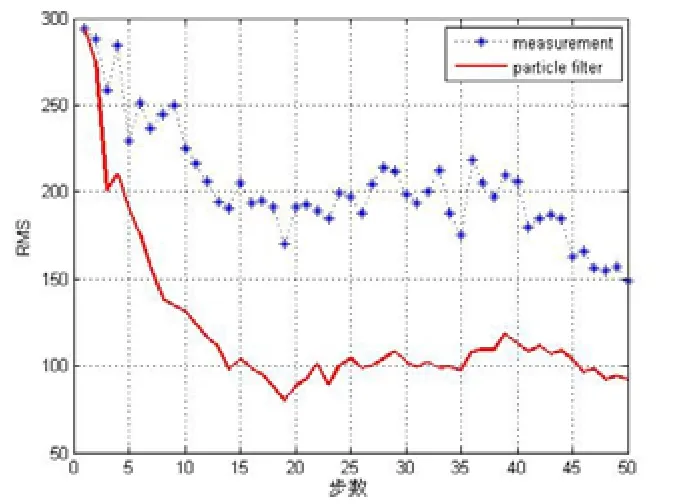
图4　100次蒙特卡洛仿真均方根误差

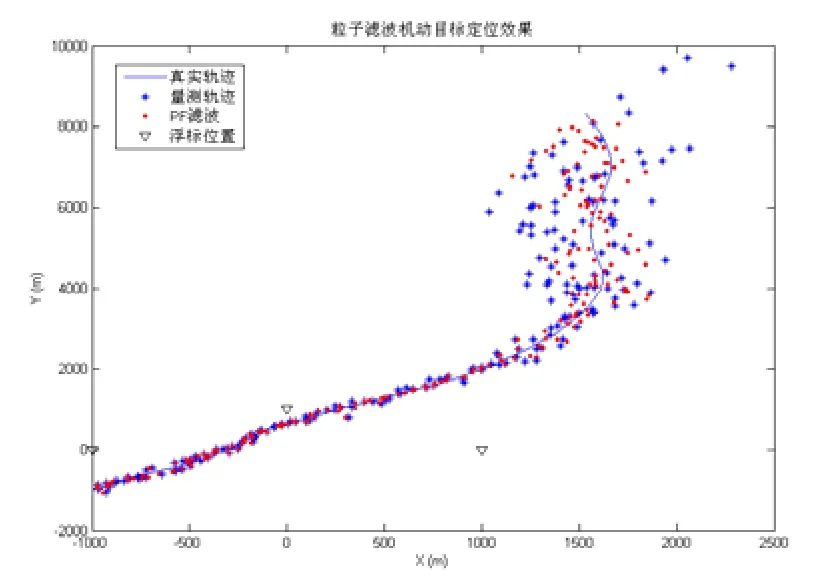
图5　机动目标跟踪结果

4　结论

基于粒子滤波的多浮标声呐联合跟踪定位算法较好的解决了观测模型以及目标运动模型的非线性，克服了传统方法线性高斯假设的束缚。如何有效地抑制退化现象和降低计算负担，需要在后续研究中进一步展开。

参考文献:

[1] RISTIC B, ARULAMPALAM S, GORDON N. Beyond kalman filters: particle filters for target tracking[M]. Norwood, MA: Artech House, 2004.

[2] BOERS Y, DRIESSEN J N. Particle filter based detection for tracking[C]. proceedings of the American Control Conference, 2001:4393-4397.

[3] 姚剑敏. 粒子滤波跟踪方法研究[D].中科院长光所,2004.

[4] 张俊根. 粒子滤波及其在目标跟踪中的应用研究[D].西安电子科技大学，2011.

[5] PUNITHAKUMAR K, KIRUBARAJAN T, SINHA A. A sequential monte carlo probability hypothesis density algorithm for multitarget track-before-detect[C]. Proc. of SPIE, 2005.