分布式基元水声目标被动定位方法研究

张学峰袁蓉安良(.9388部队94分队，湛江，540；.东南大学信息科学与工程学院，南京，0096）



分布式基元水声目标被动定位方法研究

张学峰1袁蓉1安良2
(1.91388部队94分队，湛江，524022；2.东南大学信息科学与工程学院，南京，210096）

摘要对分布式基元信号到达时差被动定位方法的性能进行了分析，仿真结果表明增大基阵孔径能够有效地提高定位精度，并且对时延估计误差和基元坐标测量误差有着很好的宽容性。利用海上实测目标声信号对分布式基元被动定位方法进行了验证。处理结果表明，该方法能够实现对远距离声源的准确定位。

关键词被动定位；TDOA；分布式基元；水声目标

基于信号到达时差（Time Difference of Arrival，TDOA）的方法被广泛应用于电磁波信号[1-3]和声信号[4-7]的被动定位技术中。特别是在水声被动定位领域，利用水声信号到达接收阵各基元的时延差进行目标位置的解算仍是一种有效的方法。近年来学者们在基于互相关的TDOA经典算法基础上加以改进，研究了新颖的信号到达时间差估计算法[8-9]，提高了被动定位算法的精度。水声基阵的阵形以及基元坐标的精度也是影响被动定位算法精度的一个重要因素。在利用信号到达各基元的TDOA解算信号源位置时，通常认为基元的坐标是确知的和不变的。然而，许多被动定位系统的基阵布放是随机的或者是动态的，基元的位置具有很强时变性，对于基于TDOA的被动定位系统来说，基元位置的偏差将导致定位性能严重下降[10]。

为了降低信号TDOA估计误差和基元坐标位置误差对定位精度的影响，增大基阵孔径是一种行之有效的方法。文献[11]提出了一种基于大孔径柔性阵的水声被动定位方法，结合阵形实时校准算法，大大提高了基于信号TDOA的水声被动定位算法精度。然而，即使采用了大孔柔性阵，基阵的尺度仍然受到承载平台的限制，其孔径与短基线定位系统的基线尺度相当。如果要实现更大的基阵孔径，必须摆脱承载平台的尺度限制，采用分布式基元的方式。

本文重点针对采用分布式基元的水声目标被动定位方法性能和可行性进行深入的分析。重点探讨了两个问题：（1）当基阵孔径增加至千米量级时，被动定位精度是否能够得到明显的提高；（2）当基阵孔径增大时，基于互相关的算法是否能够提取到稳定、有效的信号TDOA。本文分析了影响分布式基元TDOA被动定位精度的因素，并利用海上实测数据考察了分布式基元接收信号的相关性，并对利用分布式基元信号TDOA的水声目标被动定位方法进行了验证。

1 任意阵形TDOA定位算法

设有N+1个基元组成任意阵形的接收阵，各基元的位置用直角坐标ri表示，为了方便起见且不失一般性，令参考基元r0位于坐标原点，即：

声源的坐标用rs表示，r0到第i个基元和声源的距离分别用Ri和Rs表示，即：

声源到第i个基元的距离记为Di：

声源到第i个和第j个基元的距离差用dij表示，设水中声速为c，τij表示声源信号到达第i个和第j个基元的相对时延，则有：

TDOA被动定位是一个参数估计问题，未知参数向量为声源的坐标rs，观测数据为信号到达相对距离差di0，它们之间的关系用方程表示为：

其中，函数g为声程差：

将（7）式写为矩阵方程形式：

其中d=[d10,d20,…,dN0]T。选择使（10）式所示的误差平方和最小，所得的参数估计rˆs为rs的最小二乘估计。

为了解决最小二乘估计中的非线性问题，学者们提出了许多线性化的最小二乘方法，球面内插法[12]就是其中的一种，其基本思想就是引入方程误差εi：

则N个方程可以写为矩阵形式：

其中，

当Rs已知时，式（12）为声源坐标rs的线性方程，选择使方程误差式（12）最小，即可将问题转化为线性最小二乘估计。经过两重最小二乘估计[12]，可以得到声源距离和坐标的估计分别为：

其中H矩阵如（16）式所示，加权矩阵W为正定阵，初始值可取为单位阵，通过迭代算法来进行修正[12]。本文中取单位阵，即不进行加权。

2 球面内插法性能分析

由（16）式和（17）式可知，声源位置的估计精度取决于Ri、di0和S。在水声信号处理领域中，距离的测量通常转化为时延估计问题，如（6）式所示，距离差di0的估计精度取决于信号到达相对时延τi0的估计精度，而τi0的估计精度主要受到信噪比、信号带宽以及观测时间的制约[13]。S为基元的坐标，其精度受到布阵方式的限制。Ri为各基元与参考基元之间的距离，其大小决定了基阵的孔径。为了提高声源位置的估计精度，可以通过提高di0的估计精度和S的准确程度，或增大阵元之间的距离来实现。

设信号到达相对时延估计的均方误差为σt，则距离差估计的均方误差为σd=cσt，各基元的真实位置为x0(0,0,0)，x1(−L,0,0)，x2(0,L,0)，x3(L,0,0)，x4(0,−L,0)，x5(0,0, −h)，c=1 530 m/s，h=10 m。设信号到达相对时延估计误差服从N(0,σ2t)的高斯分布，利用Monte Carlo仿真不同L和σt时的声源距离Rs估计误差，结果如图1所示，声源位置Rs利用（16）式计算。由仿真结果可见：随着信号到达相对时延估计误差的增大，Rs的估计误差迅速增加，尤其是在L较小时，Rs估计结果变得很不稳定；而在L较大时，即使时延估计误差较大，仍然能够取得精度很高的Rs估计结果。

图1　距离估计误差随时延估计误差的变化

设基元坐标测量误差服从N(0,σ2d)的高斯分布，利用Monte Carlo仿真不同L和σd时的声源距离Rs估计误差，结果如图2所示，声源位置Rs利用式（16）计算。与图1所示的结果相似，较大的L值仍然对基元坐标误差有着很好的宽容性。

图2　距离估计误差随基元坐标测量误差的变化

由上述仿真结果可见，随着基阵孔径的增大，TDOA被动定位算法对时延估计误差和基元坐标误差的宽容性增强。因此，在时延估计精度和基元坐标测量精度受到限制的情况下，可以通过增大基阵孔径来实现被动定位精度的提高。但是，随着基阵孔径的增大，基于互相关处理的时延估计会遇到互相关峰模糊问题[14]，将导致时延估计发生错误。此外，上千米的孔径是无法通过固定连接的基阵实现的，必须采用分布式基元组成的基阵，此时基元位置的估计也会产生较大的误差。图3给出了大时延估计误差和大基元位置测量误差条件下的Rs估计误差变化情况，可见当L=5 000 m时，Rs的估计精度仍然很高。

图3　　大时延估计误差和基元位置误差条件下距离估计误差变化

3 实测数据处理

为了验证基于分布式基元的TODA被动定位方法的可行性和有效性，本文采用第5届国际海洋哺乳动物被动声检测、识别与定位研讨会提供的定位数据集对第2节中的定位算法进行了检验。该数据集提供了由固定在夏威夷考艾岛（the island of Kauai）海域海底的7个水听器接收的小须鲸“啵嘤”声（Boings of minke whales）信号，7个水听器的位置如图4中的P1~P7所示。选择P1为坐标原点，水听器之间的最小间距为7.36 km，最大间距为28.41 km。

图4　水听器和目标位置示意图

表1　水听器位置

该数据集提供了总时长为30 min的数据，其中包含有比较清晰的5段小须鲸“啵嘤”声。图5所示为其中一段“啵嘤”声的波形图和时频图，由时频图可见该信号是由1.28 kHz、1.39 kHz、1.50 kHz和1.62 kHz四个较强的频率分量和其它一些弱频率分量构成的宽带信号。

图5　小须鲸“啵嘤”声信号波形和时频图

由于P3和P5两个水听器接收信号的信噪比较低，在定位中没有使用。其余5路信号作为目标信号，采用球面内插法对声源进行了定位。图6~图9分别为P2、P4、P6和P7接收信号与P1接收信号之间的互相关函数，可见虽然水听器之间距离很远，但接收信号仍然保持了较好的相关性。图10为对声源的定位结果。五段“啵嘤”声开始出现的记录时间分别为2分29秒、8分46秒、14分48秒、21分6秒以及28分33秒，由于小须鲸在运动，因此五次测量的结果目标位置是不同的，与ONR给出的目标运动情况相符合[15]。

图6　P2接收信号与P1接收信号之间的互相关函数

图7　P4接收信号与P1接收信号之间的互相关函数

图8　P6接收信号与P1接收信号之间的互相关函数

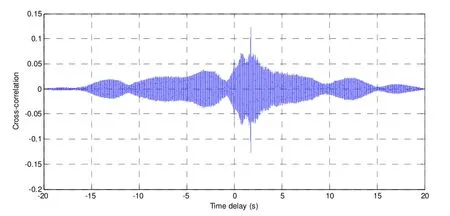
图9　P7接收信号与P1接收信号之间的互相关函数

图10　小须鲸目标定位结果

4 结论

本文讨论了基于分布式基元的水声TDOA被动定位问题。对球面内插算法定位性能进行了仿真，结果表明：利用分布式基元构成的基阵进行被动定位，算法对时延差估计误差和基元位置测量误差有着很好的宽容性。通过对实测小须鲸“啵嘤”声信号的被动定位处理，验证了利用分布式基元进行水声目标被动定位的可行性。

参考文献：

[1] MARTIN R K, YAN C P, FAN H H. Bounds on distributed TDOA-based localization of OFDM sources[C]. 2009 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Taipei, April 2009: 2290-2292.

[2] LI W C, WEI P, XIAO X C. A robust TDOA-based location method and its performance analysis [J]. Science in China (Series F: Information Sciences) , 2009, 52(5): 876-8482.

[3] 龚福祥, 王庆, 张小国. 非视距环境下的GPS/TDOA最速下降混合定位算法[J]. 仪器仪表学报, 2011, 32(7): 1500-1506.

[4] LOMBARD A, ZHENG Y H, BUCHNER H, et al. TDOA Estimation for multiple sound sources in noisy and reverberant environments using broadband independent component analysis[J]. IEEE Transactions on Audio, Speech and Language Processing, 2011, 19(6): 1490-1503.

[5] 董明荣, 许学忠, 张彤, 等. 空中炸点三基阵声学定位技术研究[J]. 兵工学报, 2010, 31(3): 343-349.

[6] 吴晓, 靳世久, 李一博, 等. 基于麦克风阵列声音信号定位方法的研究[J]. 传感技术学报, 2010,23(5): 682-686.

[7] 周明, 赵俊渭, 李金明. 一种小型水下运动目标定位系统的设计[J]. 仪器仪表学报, 2006, 27(2): 128-131.

[8] ZAMANIZADEH E, GOMES J, BIOUCAS-DIAS J M. Source localization from time-differences of arrival using high-frequency communication signals[C]. IEEE Oceans Conference, 2011: 1-9.

[9] 姜可宇, 姚直象, 尹敬湘. 一种基于三元阵的水下目标被动定位方法[J]. 兵工学报, 2012, 33(9):1107-1111.

[10] HO K C, LU X N, KOVAVISARUCH L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 684-696.

[11] 安良, 陈励军, 陆佶人, 等. 船载柔性阵基元坐标实时获取技术研究[J]. 数据采集与处理, 2010, 25(1): 86-92.

[12] SMITH J O, ABEL J S. Closed-form least-squares sources location estimation from range-difference measurements[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1987, 35(12): 1661-1669.

[13] WEINSTEIN E, WEISS A J. Fundamental limitations in passive time-delay estimation-part II: wide-band systems[J]. IEEE Trans Acoust. Speech Signal Processing, 1984; 32(5): 1064-78.

[14] 安良, 陈励军, 方世良. 水声被动定位中的互相关峰模糊现象及解模糊算法研究[J]. 电子与信息学报, 2013,35(12): 2948-2953.

[15] NOSAL E M. Passive acoustic tracking of minke whales[R]. AD, 2008: A535209.