声音在铝条中传播速度与波形图的关系探究

李清梅　陈华玲　李德安

(华南师范大学物理学，广东　广州　510000)

声音在铝条中传播速度与波形图的关系探究

李清梅陈华玲李德安

(华南师范大学物理学，广东广州510000)

摘要：研究声音在不同长度铝条传播的波形图特点，发现1米和0.5米的铝条振动波形图有很明显且分布规律的包络图。本次实验主要探究1米和0.5米铝条振动包络图的特点规律。

关键词：铝条；波形图；驻波；基频；谐频；包络图

总结前人对铝条振动发声的探究，有如下几点结论：

(1)用手捏住铝条长度的1/2n处(n为从零开始的整数)，用沾有少许松香粉的另一只手指均匀的摩擦拉动ΔL铝条，铝条会发出声音，且手离开铝条后仍有声音，声音持续时间很长.

(2)基音的波长是铝条长度的2倍，即λ=2L.

(3)对于同一根铝条，捏住1/2处(下文称为1/2节点)时，设铝条发声的频率为f0；捏住1/2n处时，频率应为f0的整数倍.

(4)铝条的长度L不同，铝条发声的频率f不同，且L与f成反比.

(5)频率f与铝条的粗细、形状无关.

为了验证以上几点结论，我们做了大量的不同长度铝条的发声实验，在这大量的实验中，我们还意外的发现1米和0.5米的铝条振动波形图有很明显的分布规律.本文主要探究1米和0.5米铝条振动的特点规律.

1实验器材

不同长度的“L”型铝条、米尺、松香、朗威DISLab、计算机、声传感器、数据采集器等.

2实验原理

2.1　铝条发声原理

手捏住铝条某部，另一只手对铝条进行摩擦时，铝条左右分别受到力F和摩擦力f的作用，铝条受力如图1(a)所示.

图1

2.2　测定声音在铝条中传播速度的原理

驻波是由入射波和反射波叠加而成，在2种介质的界面处是波腹还是波节，取决于界面两侧介质的性质.介质的密度与波速的乘积叫做波阻(即波的阻抗)，波阻相对较大的介质称为波密介质，反之称波疏介质.波从波疏介质入射而从波密介质上反射时，界面处形成波节；波从波密介质入射而从波疏介质上反射时，界面处形成波腹.

手指紧捏住铝条，不停地向相同方向抹动铝条，铝条受到纵向(沿铝条的方向)的连续扰动会产生纵波(介质振动的方向与波的传播方向相同的波)，入射波与从介质边界(铝条的两端)反射回来的反射波发生干涉，形成驻波.手捏着铝条的中点，由于手的约束，该处的介质不易做纵向振动，所以铝条中点处一定是波节.铝条的两端是2种介质(铝和空气)的界面处，铝是波密介质，空气是波疏介质，所以铝条的两端一定是波腹.因此，铝条中驻波可能有如图2所示的波形.

图2　铝条中的驻波波形

2.3　基频与谐频

在铝条中产生与驻波波长相等的声音，其中波长最大(频率最小)的声音叫基音，其他的声音叫泛音，而基音的延续时间最长，泛音很快就衰减消失，所以我们听到的持续的声音是基音.我们将基音的频率称为基频f1，泛音的频率称为高次谐波的频率简称谐频fn，其中fn=nf1.在摩擦铝条的手指还未离开铝条，铝条发出的声音是基音与泛音的叠加；当手指离开铝条，铝条发出的声音则只有基音.

3实验探究

3.1　测量声音在不同长度的铝条中的传播速度

分别取不同长度的铝条，用手捏住铝条中部，另一只手对铝条进行摩擦时铝条发声.与此同时用朗威DISLab软件及声波传感器对声音进行采集，得到铝条发声的波形图，并用朗威DISLab软件将某一部分波形图放大到可数波数的程度，然后截取一部分，得到波数n，及与之对应所用的时间t，记录数据在表1中.

3.2　探究声音在不同长度的铝条中的频率关系

如3.1操作步骤，记录发声铝条的长度L及对应的频率f.

3.3　探究不同长度的铝条的波形图

在做第二步的时候意外发现L=50cm和L=100cm的波形图有非常完美的包络图.继而探究其他的长度的会不会也有同样的波形图，实验发现只有L=50cm和L=100cm的铝条才会出现完美的包络图，并且L=100cm在手按住铝条长度的四分之一处(以下称为1/4节点)也出现完美的包络图.

图3　不同长度铝条波形图

且包络图只出现在手未离开铝条时的波形图中，当手指离开离开铝条，铝条发声只剩下基音，没有包络图出现.

3.4　探究1米和0.5米铝条包络图的规律特点

将包络图放大，数出每个包络图含有的波数，发现1米二分之一节点铝条每个包络图均含有30个左右，四分之一节点含有50个左右；0.5米二分之一节点含有80个左右.猜想：既然每个包络图含有的波数基本相同，可以直接缩小波形图，数出包络图的波数n及对应所用时间t，便可求出声音在铝条中的传播速度.

因此，我们取用DISLab采集到的100cm及50cm的铝条的波形图作如下实验：

(1)放大波形图分别测6个连续包络图含有的波数n，验证是否1米、0.5米的铝条的包络图含有的波数都是相等；记录对应所用的时间t，求出每个包络图所对应的速度，并求出每个包络图含有的平均波数n；

(2)缩小波形图，测得对应6个包络图所用时间t′，将数据记录在设计好的表格中.比较用单个包络图算出的速度更接近理论值，还是用多个包络图算出的速度更接近理论值.

4数据处理及分析

4.1　测量声音在不同长度的铝条中的传播速度

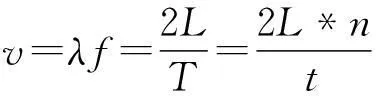
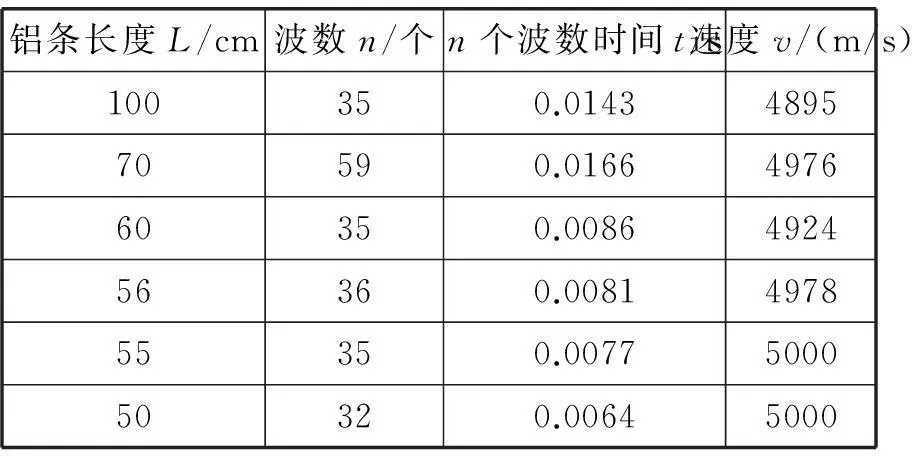
表1

结论：不同长度的铝条发声的传播速度都接近于理论值5100m/s.

4.2　探究声音在不同长度的铝条中的频率关系

实验发现，50cm的铝条中的频率接近为1m的2倍，继续做其他长度的探究，发现频率与长度间存在线性关系，如表2所示.

4.3　分析1米和0.5米包络图的特点

4.3.1L=100cm，二分之一节点处

表3为测得每个包络图包含的波数对应的声音在铝条中的传播速度.

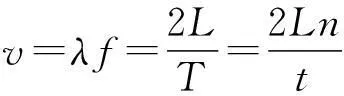
表3

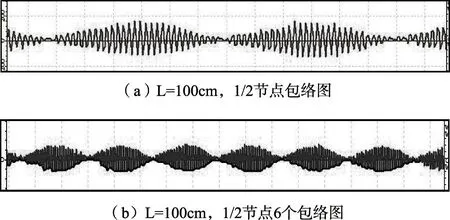
图4

4.3.2L=100cm，四分之一节点处

表4为测得每个包络图包含的波数对应的声音在铝条中的传播速度.

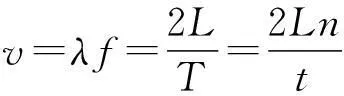
表4

图5

4.3.3L=50cm，二分之一节点处

表5为测得每个包络图包含的波数对应的声音在铝条中的传播速度.

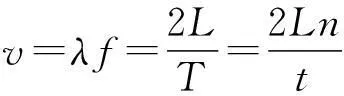
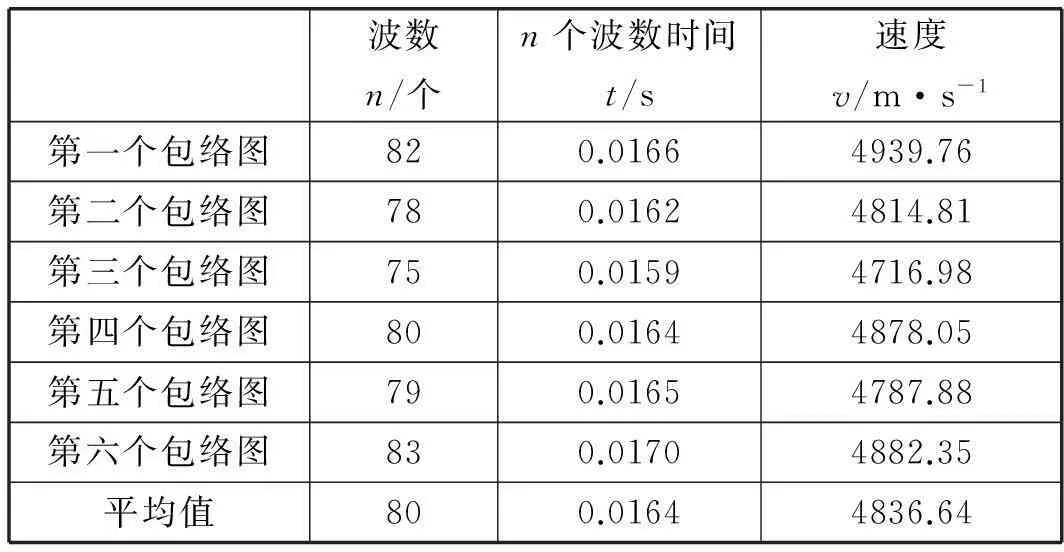
表5

图6

5实验结论

本次探究取了50cm、55cm、56cm、60cm、65cm、70cm、100cm等多根长度的铝条进行实验，并多次进行实验，结果具有可靠性.通过实验再次验证了引言所提到的声音在铝条中传播的结论.同时实验中意外的发现也让我们继续深入探究声音在铝条中传播速度与波形图的关系.发现：

(1)1米铝条(按住二分之一节点处)在非余音处波形图有包络图，每个包络图含有约32个波数；

(2)1米铝条(按住四分之一节点处)在非余音处波形图有包络图，每个包络图含有约53个波数；

(3)0.5米铝条(按住二分之一节点处)在非余音处波形图有包络图，每个包络图含有约80个波数；

(4)而除1米和0.5米的铝条具有此特点外，其他长度的铝条均没有该特点；

表6

另外，由于采集铝条声音的波形图极易受到外界环境的影响，因此需要注意以下几个方面：

(1)要在非常安静的环境下做该实验；

(2)要在较宽敞的房间内进行实验.因为在较小的房间做该实验，房间的回音会影响实验的结果；

(3)采集时要调好DISLab的采集频率，x、y的比例等；

(4)摩擦铝条要尽量均匀，且只摩擦一次或者摩擦一次后按一下铝条后再摩擦，这样可防止连续摩擦，不同次摩擦出的声音相互干扰.

6实验思考与总结

对于为什么1米、0.5米的铝条有如此完美的包络图出现，我们也查了相应的资料.据此，我们猜想：由于在非余音处，铝条的发声是基频与谐频的叠加，包络图显示了所有频率的群速，当铝条的长度及摩擦的节点满足一定的条件，便会出现包络图，具体需要利用傅里叶级数将基音泛音的函数用傅里叶级数展开计算.

经过本实验的探究，我们发现精密的实验仪器对物理新发现具有非常重要的作用，假若没有DISLab对数据的采集以及可随意调整采集后得到的波形图的比例，我们是很难发现该实验现象的.

参考文献：

[1]龙晓林，王海云.关于铝棒发声问题的探究.物理通报，2008，(4).

[2]罗志恒.铝棒发音的实验研究.物理实验，2008，(7).

[3]刘国良，杨静先.铝棒振动波动实验的理论分析.物理通报，1997，(6).

[4]曹美萍，张靖园.对驻波法测声速实验的初步探讨.物理通报，2013，(6).