DEM构建的加权最小二乘支持向量机算法

李明飞，陈传法，戴洪磊，李翼龙，李宇航

（1.山东科技大学 测绘科学与工程学院，山东 青岛 266590）

在采集数据时，由于各种条件限制造成采样数据中含有粗差，进而导致DEM[1]失真，甚至完全不能使用。为了用含粗差的数据构建出与实际地形相符合的DEM，相关科研人员提出了一系列的方法，如自适应抗差最小二乘估计方法[2]和基于最小绝对偏差的多面函数抗差方法[3]等。

SVM是以结构风险最小化原则代替经验风险最小化原则的一种机器学习方法，具有泛化能力强、精度高等优良性能。Suykens等用等式约束代替SVM的不等式约束，提出了LSSVM[4.5]，它在保持优良的泛化能力和精度的同时，拥有了更高的计算效率，可以用于海量数据的处理。文献[5]提出了LSSVM-W，通过给LSSVM的每项误差变量的二次方加上权重系数，以抑制训练样本中的异常样本。本文尝试将该LSSVM-W用于DEM建模，并将其计算精度与传统LSSVM比较，验证其可行性和高效性。

1 LSSVM-W算法

对于给定的训练数据集（xk，yk），其中，k=1，2，…，n，xk∈R为n维训练样本输入，yk∈R为训练样本的输出。为了得到基于LSSVM的抗差估计，可以利用LSSVM求出来的拉格朗日系数αk得到误差变量ek（ek=αk /γ），进而求出权重因子vk，再对LSSVM的目标函数进行修改，就得到了LSSVM-W目标函数和约束条件：

式中，ω为权向量；ek是误差变量；γ是惩罚系数；vk为权重因子；φ（·）是非线性映射，可以将样本的输入空间映射到特征空间；b是偏差量。

它们的拉格朗日函数为：

式中，αk∈R，为拉格朗日乘子。

根据KKT（ karush kuhn tucker）优化条件[6]，分别求出L关于ω、b、e、α的偏导数，并让其值为0，消去式中的ω、e，整理并改正得到矩阵方程：

式中，Ωkl=φ（xk）Tφ（xl），其中k，l=1，2，…，n；1v= [1；…；1]，为n×1的矩阵；Vγ=diag（1/γv1，…，1/γvn）。根据Mercer条件，存在映射函数φ和核函数K（，），使得K（xk，xl）=φ（xk）Tφ（xl）。为了提高其抗差性，权重因子vk的求解采用文献[7]提出的计算式：

式中，c1和c2为常数，c1=2.5，c2=3；为标准差，采用Rousseeuw[8]提出的标准差公式计算：

根据式（4）求出系数阵α，再求出误差变量的权重因子vk，重新组成LSSVM-W目标函数，这样迭代多次，直至求得稳定的α。

最后，得到LSSVM-W函数估计模型为：

LSSVM-W的算法流程为：

1）利用采集到的数据获取符合条件的（γ，σ），利用LSSVM得到系数阵α；

2）根据α计算ek及标准差，再求权重因子vk；

3）根据式（4）获得α、b；

4）重复2）～3）步，直至得到稳定的α、b；

5）给出模型函数。

2 实验分析

选择数学合成曲面为研究对象，分析LSSVM-W的抗差性。含有误差的数学合成曲面表达式为：

式中，ε为随机误差，ε=（1-θ）N（0，0.12）+θN（0，32）；污染来源为N（0，32）；被污染的正态分布为N（0，0.12）；θ为污染率，分别取值为10%、20%、30%。

横向坐标选取[-10，19.6]，纵向选取[0，30]，区域网格数为38×51，格网节点作为采样点。在实验中，随机选取1 000个点作为实验点，以剩余点作为预测点。模拟结果精度指标分别为最小误差（Min）、最大误差（Max）以及中误差（RMSE）。

确定核函数类型及参数（γ，σ）。由于模拟地形较为复杂，高斯径向基核可以准确地反映地形，可表述为：

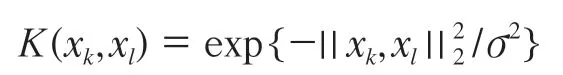
由于LSSVM-W是以LSSVM为基础，LSSVM-W和LSSVM选取的参数是一样的。在用LSSVM模拟海底趋势面[9]时，可以看出γ的选取和粗差的个数有密切联系，所以实验以粗差的个数为γ的初始值，然后固定γ，通过分组交叉验证方法[10]求出最优的σ。根据顾燕萍[11]的实验结论，正规化参数γ越大，结构风险则更侧重经验风险项，模型精度会提高。因此，最后选用采样点个数的10倍作为最终γ，这样就确定出了（γ，σ）。求LSSVM-W和LSSVM的预测模型后，得到每个格网点的模拟值，最后求出Min、Max、RMSE。

表1 LSSVM与LSSVM-W结果比较

由表1可知，当采样误差来源于被污染的正态分布时，随着污染率从10%提高到30%，LSSVM和LSSVM-W计算的RMSE都是慢慢变大的，说明二者的计算精度逐渐降低；在不同的污染率下，LSSVM-W的RMSE都比LSSVM的小，即使在污染率为30%情况下，LSSVM-W计算的RMSE都比LSSVM在10%的污染率情况下得到的RMSE值小得多，说明LSSVM-W计算精度明显高于LSSVM；LSSVM-W计算得到的Min和Max的绝对值均小于0.3，且小于LSSVM的相应值。由此可见，LSSVM-W具有较好的抗差性，是一种较好的DEM构建方法。

3 结 语

由于受采集条件的限制，采集数据中不可避免地含有粗差[12]。如果不对这些含有粗差的数据进行抑制或剔除，将会对DEM的构建精度产生严重影响。本文将LSSVM-W应用到DEM中，发展了一种构建DEM的LSSVM-W算法。通过数值模拟曲面可知，LSSVM-W方法在很大程度上抑制了粗差对曲面模拟的影响，是一种较好的DEM构建方法。

在LSSVM-W方法中，核函数的参数以及惩罚系数的选取是最关键的。但目前采用的方法需要花费很长时间才能求得最优的参数；当实验中污染率达到30%以后，得到的精度变得很低，LSSVM-W的结构有待进一步优化。

[1]陈传法,王冬,郭恒庆.DEM平均误差置信区间估计[J].中国矿业大学学报,2011,40(4):146-151

[2]陈再辉,路晓峰.基于自适应抗差最小二乘的DEM数据粗差剔除[J].海洋测绘,2006,26(6):26-28

[3]Chen C F，Li Y Y.A Robust Multiquadric Interpolation for DEM Construction[J].Mathematical Geosciences,2013,45(3):297-319

[4]Suykens J A K,Vandewalle J.Least Squares Support Vectormachine Classifiers[J].Neural Process Letters,1999,9(3):293-300

[5]Suykens J A K,Brabanter J D,Lukas L,et al.Weightedleast Squares Support Vector Machines:Robustness and Sparse Approximation[J].Neurocomputing,2002,48(1): 85-105

[6]邓乃扬,田英杰.数据挖掘中的新方法——支持向量机[M].北京:科学出版社,2006

[7]包鑫,戴连奎.加权最小二乘支持向量机稳健化迭代算法及其在光谱分析中的应用[J].化学学报,2009,67(10):60-65

[8]Rousseeuw P J,Croux C.Alternatives to the Median Absolute Deviation[J].Journal of the American Statistical Association,1993(12):73-83

[9]黄贤源,翟国君,隋立芬,等.最小二乘支持向量机在海洋测深异常值探测中的应用[J].武汉大学学报:信息科学版,2010,35(10):58-61

[10]杨敬娜.基于十折法的最小二乘支持向量机参数选取方法[J].机械工程师,2011(12):28-29

[11]顾燕萍,赵文杰,吴占松.最小二乘支持向量机的算法研究[J].清华大学学报:自然科学版,2010,50(7):157-161

[12]Rousseeuw P J,Debruyne M,Engelen S.Robustness and Outlier Detection in Chemometrics[J].Critical Reviews in Analytical Chemistry,2006,36(3-4): 221-242