电力系统无功优化模型的研究综述

王晓文, 赵彦辉

(沈阳工程学院，辽宁 沈阳 110136)



电力系统无功优化模型的研究综述

王晓文, 赵彦辉

(沈阳工程学院，辽宁 沈阳 110136)

摘要：总结了考虑系统网损最小、无功补偿设备容量最小、电压偏差最小、静态电压稳定裕度最大以及多目标加权等几种常用的经典电力系统无功优化数学模型,结合近年来关于智能电网关键技术的研究成果，分别对交直流混合输电系统、计及无功电价的电力市场、考虑负荷的变化影响及包含风电、光伏发电的分布式电源介入等智能电网背景下的无功优化模型进行综述，指出了各相关领域无功优化模型研究中存在的问题，并给出了解决方案.并就上述各研究领域中无功优化的代表性模型进行具体阐述，其中包括各种情况下无功优化的关键因素、目标函数及约束条件，并对其模型进行了评价.

关键词：电力系统;无功优化模型；智能电网

电力系统无功优化问题是由法国电气工程师Carpentier于20世纪60年代初期提出的、建立在严格数学模型上的最优潮流模型[1-2].无功优化，就是在系统结构参数、负荷有功和无功功率、有功电源出力给定的情况下，通过调节发电机无功出力、无功补偿设备出力及可调变压器的分接头，使目标函数达到最优，同时要满足各种物理和运行约束条件，如无功电源出力、节点电压幅值和可调变压器分接头位置等上、下限的限制[3].因此，无功优化本质上属于连续变量和离散变量共存的、大规模非线性混合整数规划问题[4-8].

电力系统无功优化是保证电力系统安全运行、降低系统有功损耗和维持电压正常水平的一种有效手段.传统无功优化模型的研究主要集中在常规变量约束的基础上，使单个或多个常规目标函数最优等方面.随着智能电网的发展，远距离、大容量高压直流输电系统的投入运行，计及无功电价的电力市场的出现，考虑负荷随机性的负荷预测模型的提出，包含风电、光伏发电等新能源发电的分布式电源并网等众多因素的影响，使电网结构更加复杂、电网规模更加庞大.针对智能电网背景下的新型电网，传统的无功优化模型已不能准确反映当前电力系统的实际情况，应根据智能电网的发展做出相应的改进，即建设新型智能电网，这对无功优化问题的建模提出了新的要求.

1经典无功优化模型

1.1　数学描述

进行无功优化研究，首先是建立包括目标函数和约束条件的无功优化数学模型.模型处理是无功优化的基础，电力系统无功优化的数学模型可以统一描述为

(1)

式中：u为控制变量，可包括发电机节点的无功出力、可调变压器的变比位置、无功补偿设备的补偿容量、PV节点和平衡节点的电压模值；x为状态变量，包括除平衡节点外其他所有节点的电压相角、除发电机或具有无功补偿设备外的节点电压模值；f(u,x)为无功优化的目标函数，可以从经济性、安全性、稳定性等多种角度考虑，可以是单目标优化规划，也可以是多目标优化规划；g(u,x)为等式约束条件，即节点潮流平衡方程；h(u,x)为不等式约束条件，即控制变量与状态变量必须满足运行的上、下限.

1.2　具体模型

1.2.1目标函数

电力系统无功优化根据不同优化要求，可以选择不同的优化目标函数.

1.2.1.1考虑网损的无功优化模型

从系统经济性角度出发，考虑系统网损最小为目标函数，即

(2)

式中：nl为系统总支路数；Gk(i,j)为支路i-j的电导；Ui,j分别为节点i,j的电压；θi,j分别为节点i,j的相角.

1.2.1.2设备容量的无功优化模型

从系统投资角度出发，选择无功补偿设备容量或投资总和最小为目标函数，即

(3)

式中：i为无功补偿容量可调节点；Qqi为节点i的无功补偿实际投入容量；Ci为节点i的无功补偿设备单位容量投资，当Ci=1时优化目标为无功配置容量最小.

1.2.1.3考虑电压质量的无功优化模型

从系统安全性角度出发，选取节点电压偏离规定值最小为目标函数，即

(4)

1.2.1.4考虑电压安全稳定的无功优化模型

(5)

式中δmin为系统收敛潮流雅可比矩阵的最小奇异值.

1.2.1.5考虑多目标加权的无功优化模型

在对以上经典模型的各个目标函数归一化处理的基础上，通过合理选择权系数，建立了考虑多目标加权的无功优化模型，最终目标函数为：

(6)

目标函数归一化处理：

(7)

1.2.2约束条件

1.2.2.1等式约束条件

考虑系统节点潮流平衡的方程约束为

(8)

式中:PGi,QGi分别为发电机节点的有功和无功出力；PLi,QLi分别为负荷节点的有功和无功功率；QCi为无功补偿装置的补偿容量；Gij,Bij,θij分别为节点i,j之间的电导、电纳和电压相角差；N为系统总节点数.

1.2.2.2不等式约束条件

不等式约束可分为控制变量约束和状态变量约束.控制变量约束为

(9)

状态变量约束为

(10)

式中:QGi,QGi.max,QGi.min分别为发电机节点i无功出力及其上、下限值；QCj,QCj.max,QCj.min分别为第j组无功补偿装置的补偿容量及其上、下限值；Ttk,Ttk.max,Ttk.min分别为第k台有载调压变压器变比及其上、下限值；Ui,Ui.max,Ui.min分别为节点i电压模值及其上、下限值；δij，δij.max，δij.min分别为节点i和j之间的电压相角差及其上、下限值；Ng，Nt，Nc，N分别为发电机节点数、有载调压变压器可调分接头数、电容器投切组数、系统节点数.

2交直流混合输电系统的无功优化模型

交直流并联电网的无功优化问题与传统交流电网无功优化问题有很大不同，纯交流电网主要是通过合理配置系统无功以降低有功网损，而交直流并联电网则是通过调整直流功率改变有功潮流分布以降低网络损耗.现有无功优化方面的研究主要集中在纯交流系统的静态与动态无功优化方面[9-12]，而就交直流系统的无功优化方面的研究较少.

文献[13]根据交直流潮流分布对系统网损的影响机理，建立了大型交直流并联输电网网损优化的最优潮流模型，提出了大规模互联电网的在线网损优化计算方法，并将该模型和算法在南方电网中进行了实际应用，有效降低了南方电网主网的网损，具有较高的实用价值.为了克服交直流混合输电系统中交直流间的相互影响，保证整个系统的合理运行，文献[14]在给定有功调度前提下，提出了考虑电压指标、有功网损等综合因素效益最佳的交直流混合输电系统无功优化模型，优化变量引入直流部分换流器的控制电压、控制电流、控制功率，以及换流变压器变比.利用混合智能算法求解该优化模型，并通过IEEE9节点系统的交直流算例分析，验证了该模型的正确性以及算法的收敛性和有效性.

文献[13-14]研究的是交直流混合输电系统的静态无功优化模型，没有充分考虑直流控制方式的优化选择以及交直流输电通道传输功率的协调分配问题.为了解决这一问题，颜伟等在常规交流系统的动态无功优化模型基础上建立了交直流系统的动态无功优化模型[15]，其模型如下.

2.1　目标函数

目标函数取全天24 h能量损耗最小，即

(11)

式中：SL,ST,φdL分别为交流系统线路集合、变压器支路集合、直流系统支路集合；ij为节点i与j之间的支路；ΔPLij,t,ΔPTij,t,ΔPdij,t分别为第t个时段交流系统、变压器支路、直流系统的功率损耗.

2.2　约束条件

2.2.1交流系统的运行约束

交直流混合输电系统的交流运行约束和控制约束同传统的交流系统，另外增加了电容器和变压器的动作次数约束.

电容器开关动作次数约束为

(12)

有载调压变压器动作次数约束为

(13)

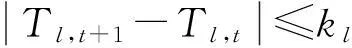
(14)

式中：Cm,t为次日第m个电容器开关t时段的状态，1为闭合，0为断开，⊕为异或运算符；Tl,t为次日第l个有载调压变压器的分接头t时段的挡位值;Mm为第m个电容器开关的日允许最大动作次数；Kl为第l个有载调压变压器的日允许最大动作次数;kl为有载调压变压器相邻时段最大动作次数(分接头每调一挡即动作一次).

2.2.2交直流系统的关联约束

交直流系统的关联约束即为交直流电网连接节点的功率平衡方程，

(15)

式中：i∈φd，φd为交直流电网连接节点的集合；Pdi,t和Qdi,t分别为第t个时段换流器i的有功和无功功率；当换流器i为整流器时，sPi=1，为逆变器时，sPi=-1.但是无论是用来整流还是逆变均需要吸收无功功率，即sQi=1.

2.2.3直流系统的运行约束

换流器的基本方程为[16]

(16)

式中：i∈φd；kdi,t，kbi,t，kpi,t分别为第t个时段换流器i的变比、个数和极数；Vi,t为第t个时段连接节点i的电压幅值；θdi,t为第t个时段的控制角；xdi,t为换相电抗；Vdi,t和Idi,t分别为第t个时段直流系统i侧的直流电压和电流；Sdi,t为第t个时段换流器i的视在功率；考虑换相重叠现象引入系数η=0.995.

直流系统的控制约束为Vdi,t,Idi,t,Pdi,t,cosθdi,t,kdi,t等变量的上、下限值约束.换流器的动作次数约束同式(13)和式(14)，即

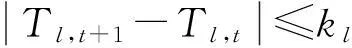
上述模型中，以交直流系统全天网损最小为目标函数，交直流系统的潮流方程约束、控制变量约束、离散变量的动态调节次数约束及节点电压的限值约束等为约束条件，建立了交直流系统的多时段动态无功优化模型.采用交直流系统的动态无功优化的混合智能算法求解该模型，对PSASP36节点系统进行动态无功优化仿真计算，结果验证了模型和算法的有效性，也表明了动态无功优化在交直流混合输电系统中具有更大的降损效益.

3电力市场环境下的无功优化模型

电力市场环境下，实行厂网分开、竞价上网，为保证电网和电厂的经济利益，应建立一种考虑无功有价性的无功优化模型[17-18].

为了得到合理的无功功率价格，文献[19]在最新潮流模型中引入了无功功率发电成本和无功补偿器成本，建立了以有功和无功发电总成本最小为目标函数的无功优化模型.对一个5节点实例系统进行仿真计算，得出了电力市场下无功电价的一些基本规律.但该文献没有考虑负荷随无功价格的波动而变化的问题.为了解决这一问题，李林川等提出了考虑无功价格的电力市场环境下的无功优化模型[20]，其模型如下.

3.1　目标函数

以有功网损费用和无功支出费用为目标函数，即

(17)

式中：λloss为有功边际价格；Ploss为有功网损；fQk(QGk)为第k个非电网公司所属无功电源无功支出费用,可以采用发电机发送无功分段报价的形式进行计费;Gs为无功电源的总个数.

3.2　约束条件

该模型的约束条件同经典无功优化模型.文献[20]采用遗传算法和ALOPEX算法相结合的混合算法对模型进行求解，并对IEEE30节点系统进行仿真分析.结果表明，无功计价对无功分布影响较大，既改善了发电机的运行工况，又使无功补偿设备得到了充分利用.

随着对电力市场研究的不断深入，电力系统各种经济调度理论将随着电力市场的变化而相应地改变.文献[21]在计及系统无功电价的基础上，建立以有功网损和无功支出综合费用最小为目标函数的电力市场下的无功优化模型，采用智能优化算法分别对IEEE14,IEEE30节点系统进行仿真计算，结果表明,该模型的适用性和经济性较好.

4考虑负荷变化影响的无功优化模型

考虑负荷变化影响的无功优化常需对未来多时段进行负荷预测.负荷本身的周期性和随机性往往会导致负荷预测结果的不确定性.文献[22]提出了特定时段的静态无功优化模型和实时环境下的动态无功优化模型.随着负荷水平的波动，静态模型易导致可调变压器抽头和补偿装置的频繁调整和投切操作.为了解决这一问题，在动态无功优化模型中引入变压器抽头和补偿装置投切开关允许动作次数约束.

大多数研究均是把一天机械地分成多个时段，将时变动态无功优化模型转化为若干个静态无功优化模型进行求解，显然精确度不高，且操作设备的动作次数降低不明显.为了降低该模型在单个时段内静态无功优化问题的复杂性，文献[23]利用遗传算法对负荷曲线进行智能分段，来解决设备动作次数约束问题，进而把时变无功优化转化为几个较大时段上的静态无功优化.以一天24个自然时段有功网损之和最小为目标函数，各个时段自身的运行约束和控制设备操作次数约束为约束条件，建立电力系统时变无功优化模型.通过IEEE30节点系统算例分析，有效地减少了无功补偿设备和变压器分接头的动作次数，明显降低了系统网损.

无论是特定时段的静态无功优化或者实时环境下的动态无功优化问题的研究大多是集中在目标函数的选取和优化算法的改进等方面，采用的大都是单一确定的负荷模型，而涉及负荷不确定性的研究相对较少，这就可能会导致收敛性差甚至不收敛.因此，有必要在无功优化中计及负荷不确定性的影响，针对这一问题，谢开贵等提出了一种计及负荷不确定性等影响因素的无功优化模型[24]，其模型如下.

4.1　目标函数

将系统有功网损、变压器和补偿设备的调节代价以及以罚函数形式进行惩罚的节点电压越限和发电机无功出力越限等作为目标函数，即

(18)

其中:

(19)

(20)

式中：PL为系统有功网损；N,NT,NC,NG分别为系统节点总数、可调变压器总数、补偿节点总数、发电机节点总数；λT,λC,λU,λG分别为可调变压器调节罚因子、补偿设备调节罚因子、电压越限罚因子、发电机无功越限罚因子.

4.2　约束条件

该模型的约束条件同经典无功优化模型.该文献将控制设备允许操作次数的调节代价和节点电压越限的罚函数计入以系统有功网损最小为目标函数的无功优化模型中，决策者可对罚函数因子进行取值以满足自身的不同需求.考虑负荷不确定性等影响因素，以克服单一负荷水平下无功优化模型不能全面描述负荷随机特性的缺点.针对无功优化模型的多目标、多约束特性，采用遗传算法对IEEE30节点系统进行求解，结果验证了该模型的正确性和可行性.

5考虑分布式电源接入的无功优化模型

分布式电源并网改变了电网的结构和运行方式，打破了电网潮流的单向流动性.大量不同类型的分布式电源的接入，可能引起地区电网电压波动较大和无功潮流分布不合理，这就给无功优化问题的建模提出了新的要求.

5.1　包含风力发电系统的无功优化模型

目前，大型风电机组常采用结构简单、并网方便的异步发电机形式，但其本身无励磁装置，启动时需要从电网或电容器吸收无功，从而影响电网的无功分布和电压稳定.针对风电以异步发电机模型并网引起的无功分布和电压稳定问题，文献[25]进行了含风电场节点的潮流计算，得出风电并网点所需的无功补偿容量，进而在满足无功需求的前提下，建立了以系统有功网损最小为目标函数的无功优化模型，采用遗传算法对IEEE30节点系统进行仿真，计算结果表明，风电场的输出功率和电压随风速的变化而变化，无功优化的结果也随之变化.

在传统配电网无功优化中，负荷波动是影响其优化结果的主要不确定因素，当风电并网后，由于风力的随机性和间歇性等非线性特点[26],致使风电机组的输出功率随风速频繁波动，进一步增加了配电网中的不确定因素.风电输出功率的变化主要依赖于风速的变化.文献[27]考虑了风速变化随机性的特点，建立了以系统网损、静态电压稳定裕度和电压平均偏离为目标函数的多目标无功优化模型，以IEEE57节点系统为算例，运用改进遗传内点算法求解含风电场的无功优化模型，有效避免了算法早熟和局部收敛问题，引入对数障碍函数，改善了节点电压越限问题.

5.1.1无功优化综合指标

相比负荷，风速变化更加频繁且很难精确预测，但风速变化具有统计特征.针对风电并网对配电网电压质量及电压调节模式带来的较大影响，陈海炎等运用概率场景决策法研究含风电的配电网无功优化问题，提出了一种由网损和静态电压稳定裕度构成的基于场景发生概率的无功优化综合指标[28]，其综合指标为

(21)

其中

(22)

将综合指标进行归一化处理可得：网损期望值越小，静态电压稳定裕度越大，综合指标λ值就越小，优化效果就越好.

5.1.2无功优化数学模型

以该无功优化综合指标最小作为目标函数，选取配电网中可调变压器抽头和电容器投运组数作为控制变量，建立了一种计及风电影响的配电网无功优化模型[28]，即

(23)

根据风电机组的特点，该文献将其按电压静特性节点进行处理，并采用自适应权重的遗传算法进行求解，以IEEE69节点系统作为测试系统进行仿真.结果表明，该模型和算法具有可行性，对包含分布式电源的配电网运行具有一定的参考价值.

5.2　包含光伏发电系统的无功优化模型

对含有光伏电站的低压配电网，有功功率和无功功率变动同时引起电压波动，影响输电线路上的电压降，对含光伏电站的配电网进行无功补偿，在一定程度上可以弥补有功功率变动造成的电压波动问题.文献[29]将光伏电站的无功功率作为无功优化的控制变量，以系统网损最小为目标函数，潮流方程为等式约束，控制变量和状态变量约束为不等式约束，建立了含光伏电站的配电网无功优化模型.采用智能单粒子优化算法进行求解，并对改进的IEEE33节点系统进行算例分析，结果表明,利用分布式电源对电网进行无功补偿能较大程度地降低系统的有功网损，并验证了该模型和算法的正确性和有效性.

为了解决光伏发电输出功率的不确定性问题，文献[30]通过采用概率论方法求得光伏电站有功功率的期望值加以解决，对并网系统逆变器的相关参数进行调整，确定光伏电站的无功出力.以系统有功网损最小为目标函数，并采用罚函数对负荷节点电压越限项进行惩罚，建立了含光伏电站的配电网无功优化模型，采用改进的细菌群体趋药性算法进行求解，并以改进的IEEE33节点配电系统为算例进行仿真分析，验证了模型和算法的有效性，但该模型仅考虑了网损最小的单目标优化问题，并没有将电压质量计入其中.

随着光伏发电的发展，越来越多的光伏电站接入配电网，光伏电站出力的随机性使得含光伏电站的配电网节点电压也具有随机性.为了解决这种随机性影响和传统无功优化模型中确定电压约束的不精确问题，郭康等以光伏电站的无功功率为控制变量，系统有功网损期望值最小为目标函数，建立了计及光伏电站随机出力的配电网无功优化模型[31]，其模型如下.

5.2.1目标函数

以系统网损最小为目标函数，引入含有电压越限惩罚项的罚函数进行修正，其目标函数为

(24)

(25)

式中：Ploss为系统有功网损期望值；Ui为节点电压；λ为罚系数；β为置信水平.

5.2.2约束条件

5.2.2.1等式约束

等式约束即节点潮流平衡方程，同式(8),即

5.2.2.2不等式约束

控制变量约束为

(26)

式中QDGk，QCi，VRj分别为光伏电站的无功容量、无功补偿设备的补偿容量、有载调压变压器变比.

状态变量约束为

(27)

该文献采用随机潮流算法求解各节点电压的概率分布，并对其进行机会约束，较好地解决了系统中光伏电站出力随机性与无功补偿设备投入确定性、光伏电站无功输出连续性和变压器分接头调节以及电容器组投切离散性之间的关系.通过IEEE33和IEEE69节点配电系统进行优化计算，使得优化结果在节点电压置信水平内都能满足电压要求，并且有效降低了系统网损，验证了该模型的正确性和适用性.

6结语

1)随着电力系统的日益复杂化，同时考虑系统经济性、安全性和稳定性的多目标加权无功优化模型是近年来经典无功优化模型研究的重点.

2)交直流混合输电系统无功优化模型的研究大多数是针对静态模型的，考虑直流输电系统对功率与电压调节能力的动态模型研究相对较少，有待于进一步研究.

3)随着电力市场的建立与完善，考虑无功电价的电力市场下负荷确定的无功优化模型研究较为成熟，但负荷随无功电价波动而变化的模型研究相对薄弱，也是该领域研究的一个难点.

4)考虑负荷变化影响的无功优化模型研究大多集中在静态和机械的动态模型方面，并且都是单一确定的负荷模型，建立针对负荷不确定性实时环境下的动态无功优化模型是该领域无功优化模型研究中的一个亟待解决的问题.

5)分布式电源并网改变了电网结构和运行方式，给无功优化问题的建模提出了新的要求.负荷的波动性、风电机组输出功率的不确定性、光伏电站出力的随机性等因素使含分布式电源接入的配电网无功优化模型建立更加复杂，这是近年来无功优化模型研究的一个热点问题.

参考文献

[1]Shoults R R,Sun D T.Optimal power flow based uponP-Qdecomposition[J].Power Apparatus and Systems,IEEE Transactions on,1982,PAS-101(2):397-405.

[2]Mamandur K C,Chenoweth R D.Optional control of reactive power flow for improvement in voltage profiles and for real power loss minimization[J].IEEE Transactions on PAS,1981,100(7):3185-3194.

[3]赵尤新,徐国禹．用敏感度方法分析计算电力系统无功和电压最优控制问题[J]．重庆大学学报，1985，8(4)：1-11．

[4]Liu W H,Papalexopoulos A D,Tinney W F.Discrete shunt controls in a Newton optimal power flow[J].Power Systems,IEEE Transactions on,1992,7(4):1509-1518.

[5]丁晓莺,王锡凡,张显，等．基于内点割平面法的混合整数最优潮流算法[J]．中国电机工程学报，2004，24(2)：1-7．

[6]Liu M B,Tso S K,Cheng Y.An extended nonlinear primal-dual interior-point algorithm for reactive-power optimization of large-scale power systems with discrete control variables[J].Power Engineering Review,IEEE,2002,22(9):56-56.

[7]程莹,刘明波．求解离散无功优化的非线性原—对偶内点算法[J]．电力系统自动化，2001，25(9)：23-27,60．

[8]程莹,刘明波．含离散控制变量的大规模电力系统无功优化[J]．中国电机工程学报，2002，22(5)：54-60．

[9]胡泽春,王锡凡．配电网无功优化的分时段控制策略[J]．电力系统自动化，2002，26(6)：45-49．

[10]王秀丽,李正文,胡泽春．高压配电网无功/电压的日分段综合优化控制[J]．电力系统自动化，2006，30(7)：5-9．

[11]Yan Wei,Yu Juan,Yu D C,et al.A new optimal reactive power flow model in rectangular form and its solution by predictor corrector primal dual interior point method[J]. Power Systems,IEEE Transactions on,2006,21(1):61-67.

[12]颜伟,田甜,张海兵，等．考虑相邻时段投切次数约束的动态无功优化启发式策略[J]．电力系统自动化，2008，32(10)：71-75．

[13]刘恺,陈亦平,张昆，等．大型交直流并联输电网网损优化理论及其在南方电网中的实现[J]．中国电机工程学报，2014，34(1)：130-137．

[14]彭磊,张建平,吴耀武，等．基于GA,PSO结合算法的交直流系统无功优化[J]．高电压技术，2006，32(4)：78-81．

[15]颜伟,张海兵,田甜，等．交直流系统的动态无功优化[J]．电力系统自动化，2009，33(10)：43-46．

[16]Yu Juan,Yan Wei,LI Wenyuan.Quadratic models of AC-DC power flow and optimal reactive power flow with HVDC controls[J].Electric Power Systems Research,2008,78(3):302-310.

[17]Meliopoulos A P S，Asad M A，Cokkinides G J.Issues for reactive power and voltage control pricing in a deregulated enviromment[C]∥System Sciences,1999,HICSS-32.

[18]Dona V M,Paredes A N.Reactive power pricing in competitive electric markets using the transmission losses function[C]∥Power Tech Proceedings,2001 IEEE Porto,2001,1:6.

[19]戴彦,倪以信,文福拴，等．电力市场下的无功电价研究[J]．电力系统自动化，2000，25(5)：9-14,53．

[20]黄志刚,李林川,杨理，等．电力市场环境下的无功优化模型及其求解方法[J]．中国电机工程学报，2003，23(12)：79-83．

[21]王正风,徐先勇,唐宗全．电力市场下的无功优化规划[J]．电工技术杂志，2000(6)：10-12．

[22]张勇军,俞悦,任震，等．实时环境下动态无功优化建模研究[J]．电网技术，2004，28(12)：12-15．

[23]沈茂亚,丁晓群,王仲达，等．电力系统时变无功优化算法[J]．电力系统及其自动化学报，2007，19(4)：84-87,92．

[24]谢开贵,肖畅．计及负荷不确定性的无功优化模型与算法[J]．电力系统保护与控制，2011，39(4)：18-22,29．

[25]胡敏,周任军,杨洪明，等．考虑风力发电的系统无功优化模型和算法[J]．长沙理工大学学报(自然科学版)，2009，6(1)：43-48．

[26]朱雪凌,刘林飞,周伦燕．风力发电并网对电网的影响[J]．华北水利水电学院学报，2010，31(6)：94-97．

[27]魏希文,邱晓燕,李兴源，等．含风电场的电网多目标无功优化[J]．电力系统保护与控制，2010，38(17)：107-111．

[28]陈海焱,陈金富,段献忠．含风电机组的配电网无功优化[J]．中国电机工程学报，2008，28(7)：40-45．

[29]郭康,徐玉琴,张丽，等．基于智能单粒子算法的含光伏电站配电网的无功优化[J]．电力科学与工程，2011，27(8)：28-32．

[30]任新伟,徐建政,赵斌．含光伏电站的配电网无功优化[J]．电力电容器与无功补偿，2014，35(1)：12-15,24．

[31]郭康,徐玉琴,张丽，等．计及光伏电站随机出力的配电网无功优化[J]．电力系统保护与控制，2012，40(10)：53-58．

(责任编辑：杜明侠)

Summary on Reactive Power Optimization Models in Electric System

WANG Xiaowen, ZHAO Yanhui

(Shenyang Institute of Engineering, Shenyang 110136, China)

Abstract:This paper gives a summary on several classical mathematical models of reactive power optimization, such as the model of minimum system network losses, the model of minimum capacity of reactive power compensation equipment, the model of minimum voltage deviation, the model of maximum stability margin of static voltage, and the model of multi-objective weighted, and so on. According to the research results for relevant literature, and combining with the key technologies of smart grid in recent years, the reactive power optimization models are respectively summarized under the background of smart grid on AC/DC hybrid transmission system, power market by taking into account reactive power price, considering the influence of load variation, the involvement of distributed-generation sources including wind power and photovoltaic generation. Some problems in the researches of reactive power optimization models are pointed out, and the solutions are provided. The representative models of reactive power optimization in the above research field are elaborated, meanwhile the key factors of reactive power optimization, the objective functions and constraint conditions are also summarized, at last, their models are evaluated.

Keywords:electric system; reactive power optimization model; smart grid

中图分类号：TM744

文献标识码：A

文章编号：1002-5634(2015)02-0063-07

DOI:10.3969/j.issn.1002-5634.2015.02.014

作者简介：王晓文(1966—)，女，辽宁锦州人，教授，硕士生导师，主要从事电力系统运行与控制方面的研究.

收稿日期:2014-09-30