基于可靠性的设备维护策略研究
余斌
(合肥工业大学 机械与汽车工程学院,合肥 230009)
0 引言
设备是企业重要的制造资源。对企业来说,有效的设备维护计划能够较大程度上提高设备可靠性,保证生产活动的顺利进行。从20世纪60年代开始,关于设备维护方面的研究逐渐成为热点,大量学者致力于以时间为主的等周期维护模型的构建,但此类维护模型没有考虑设备可靠性的要求,使得设备在后期运行过程中故障次数增加。基于可靠度的预防维护策略在提高系统可靠性方面起了重要作用[1]。 Nakagaw2]优化了前人的研究,建立了维护时间间隔逐渐变小的维护模型。Le[3]则提出了适用于多状态系统的视情维护策略,整体上降低了系统的维护费用。文献[4]将设备维护工作分为不同阶段进行维护策略的优化分析。
本文在借鉴现有研究成果的基础上,全面考虑维护过程中的预防维修成本、小修成本、置换成本、停机成本等因素,提出一种以设备可靠性为中心的设备维护优化策略,达到设备寿命周期内的期望平均维护总成本最小的目的。
1 设备维护问题描述与假设
设备维护过程中涉及到三种维修方法:预防维修、小修和置换。设备维护问题的目的是在设备维护过程中对预防维修、小修与置换三种维修方法做出合理选择与时间安排[5]。预防维修又包括定期维修与状态维修,本文选择状态维修代表预防维修,将系统可靠度作为维修决策依据。
于是将设备维护问题描述为:设备在整个寿命周期内采用预防维修方法对设备进行维护,设定最优预防维修周期数为N,第i-1与第i个预防维修周期时间间隔为Ti(i=1,2,…,N)。在前N-1次维护工作中,当系统可靠度达到事先设定的阈值R时对设备进行预防维修,在第N次达到阈值R时对设备进行置换,若设备在预防维修周期内出现失效,则采取小修使其恢复到维修前的状态(如图1)。该模型满足如下假设:1)初始状态为全新的系统;2)系统状态可实时监控与诊断;3)系统失效随机且能及时被监测出来;4)能够获取系统可靠度情况;5)系统的失效可用数学函数描述。

图1 设备维护过程
2 相关变量优化
2.1 系统失效率的优化
本文结合役龄递减因子与失效率递增因子描述系统衰退特性,参照文献[6]对系统失效率函数h(t)进行优化:

式中:hi(t)是第i-1与第i个预防维修周期内的系统失效率;役龄递减因子αi与失效率递增因子bi可以通过统计分析设备的历史运行数据得到[7]。
2.2 小修成本的优化
在以往模型中一般将小修成本看作固定费用。而在实际生产环境下,设备使用时间越久,失效后进行小修所需的成本越高。假定小修能使设备恢复到失效前的状态,并对其失效率没有影响。本文考虑因预防维修后设备的改善效果,提出改善因子模型,利用改善因子构造小修成本与维修效果之间的函数关系。设定改善因子为

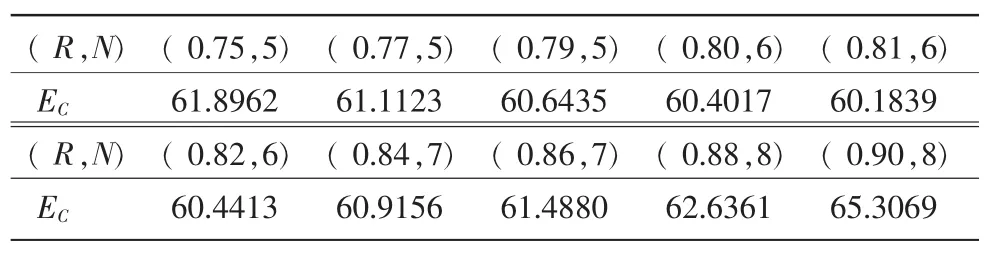
式中:0 其中,1≤i 在实际生产过程中,设备进行预防维修或者小修势必造成停机,从而产生停机成本。在现有的维护模型中,很多都忽略了设备的维护活动产生的停机损失。本文假设每次预防维修时间为Tp与小修时间为Tr,得到第i-1与第i个周期内停机成本函数: 其中,1≤i 根据可靠性理论,系统可靠度与失效率之间的关系为 在本模型中,当系统可靠度达到阈值R时实施预防维修工作,结合式(1)可得 根据以上假设,第i-1与第i个周期内的期望维护总成本可表示为 式中,1≤i 结合式(8)和式(9),得到设备整个维护过程中的期望平均总成本为 在实际生产过程中,设备不可能无限期地进行预防维修而不被置换。本文在求解该模型时限制设备预防维修周期的上限,并在给定的可靠度范围[0.6,1]内计算最小期望平均总成本,最后得到可靠度阈值R′以及预防维修次数 N′组成( R′,N′)作为设备最佳维护策略,并得到该维护策略下对应的周期Ti。 假定设备系统失效率服从被工业生产广泛采用的威布尔分布: 式中:t≥0;形状参数k=3;尺度参数λ=100。设定设备预防维修周期上限为10,预防维修时间Tp=2,预防维修费用Cp=350,单次小修时间Tr=1,第一个预防维修周期内的小修费用Cr(1)=Cr=1800,单位停机成本Co=150,置换成本C=10 000。参照设备维护历史数据,设定役龄递减因子αi=3i/(7i+11),失效率递增因子bi=(11i+7)/(9i+8)。在改善因子中,假定成本调节系数u=2/35,时间调节系数v=0.095,学习效应调节系数w=-0.337,结合上文所给的设备维护模型,利用MATLAB软件计算,得到表1和图2所示结果。 表1 部分维护策略下的EC 图 2 E c随( R,N)变化图 计算得到得(0.81,6)对应的EC=60.1839最小,所以(0.81,6)为设备最佳维护策略,所以当设备第6次达到系统可靠度阈值0.81时对设备进行置换。在表1中,随着系统对可靠性要求的提高,最佳预防维修周期次数也随之增加,这与设备的实际维护过程吻合。 表2 最佳维护策略下的预防维修周期 在最佳维护策略下相应的预防维修周期如表2。 由表2可知,在最佳维护策略(0.81,6)下的预防维修周期呈现出递减趋势,这反映出设备的衰退特性。即随着设备运行时间的增加,需要对设备进行更加频繁的维护来确保系统的可靠度,结果与实际情况相符。 本文综合考虑设备实际维护过程中的影响因素,提出了一种新的设备维护数学模型,达到了设备寿命周期内成本率最小的目的,计算结果表明该模型能够兼顾维护成本的同时保证设备可靠性,有助于解决实际生产中的设备维护决策问题。 [ 1] Moghaddam K S,Usher J S.Preventive maintenance and replacement scheduling for repairable and maintainable systems using dynamic programming [ J].Computers and Industrial Engineering,2011,60( 4):654-665. [ 2] Nakagawa T.Sequential imperfect preventive maintenance policies[ J].IEEE Trans on Reliab,1988,37( 3) :295-298. [ 3] Le M D,Tan C M.Optimal maintenance strategy of deteriorating system under imperfect maintenance and inspection using mixed inspection scheduling [J].Reliability Engineering & System Safety,2013,113( 1) :21-29. [4] 曲玉祥,吴甦.基于不完全维护的劣化系统分阶段顺序预防维护策略[ J].机械工程学报,2011,47( 10) :164-170. [5] Nakagawa T.Maintenance theory of reliability [M].Springer Science& Business Media,2006. [6] 奚立峰,周晓军,李杰.有限区间内设备顺序预防性维护策略研究[ J].计算机集成制造系统,2005,11( 10):1465-1468. [7] 周晓军,奚立峰,李杰.一种基于可靠性的设备顺序预防性维护模型[ J].上海交通大学学报,2005,39( 12):2044-2047.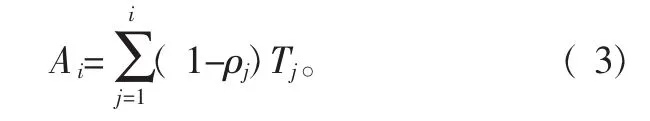
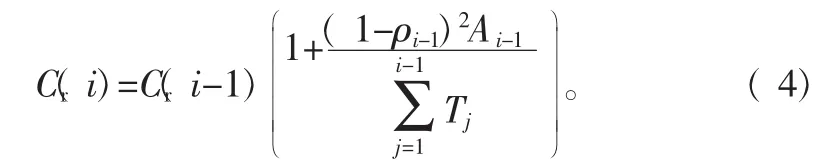
2.3 停机成本
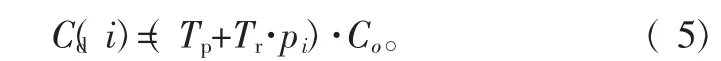
3 设备维护数学模型构建
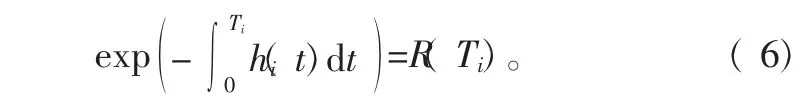
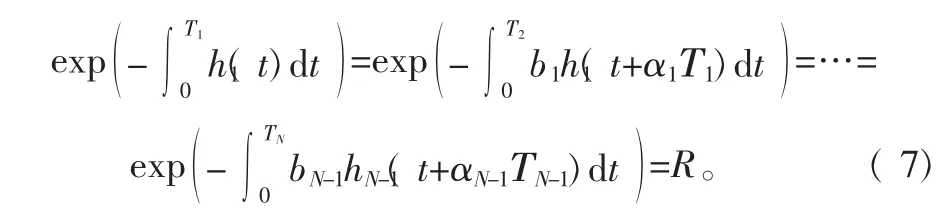
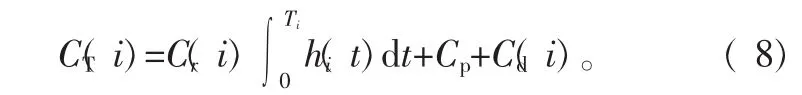
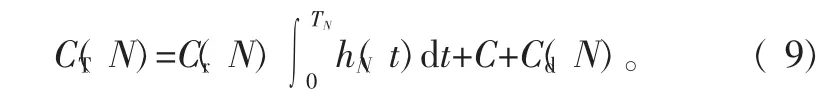
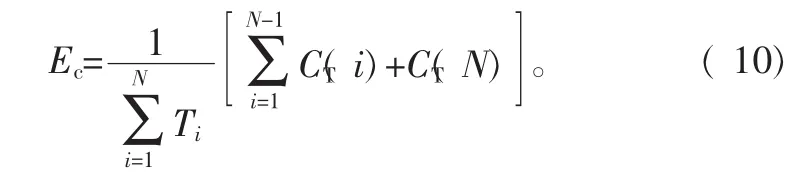
4 算例分析
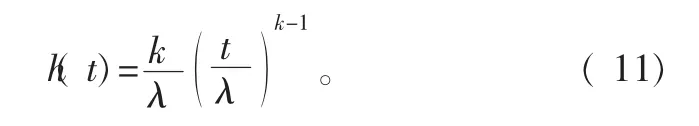


5 结 语

