基于旋量理论的机械手并联机构刚度分析

张海英， 范进桢

（宁波职业技术学院，浙江 宁波 315800）

0 引 言

在现代化的加工车间，常配有工业机械手，用机械手代替人工完成如搬运、装配、切割、喷染等作业，以提高生产效率，完成工人难以完成的或者危险的工作。

而刚度在很大程度上影响着机构的动态性能和末端的定位精度，所以刚度问题是设计和评价机构的一项重要指标，因此建立机构的静刚度矩阵依此来分析机构的刚度问题非常重要［1］。通过对机构的刚度分析可以了解机构是否有足够的刚度来承受一定的载荷，为机构的优化设计和控制方案设计做理论准备。本文采用旋量理论来分析机械手并联机构的刚度问题。

1 机构描述

冲床机械手能适用于多工位冲压生产线，为了完成圆形工件的取放操作，设计了一个机械手爪用于精确取放工件，该机械手手爪的机构图如图1所示，共有7个部分组成，其中手指5有3根，都采用轧制铝材料。手指支架4在丝杆7的带动下上下移动，可使抓手连杆3和手指 5在空间 360°内张缩运动。

2 机械手并联机构刚度分析

柔性机构是一种靠构件元素或单元具有的柔性来输出运动或里的机构，柔性铰链机构和分布柔度全柔性机构是其中的两种主要类型［2］。 复杂柔性机构的刚度分析是建立在单元柔性单元刚度矩阵基础上的，对于并联机构而言，末端刚度是先把所有支链的刚度变换到同一坐标系下，再把各个支链的刚度相加［3］。

2.1 单元柔性单元刚度矩阵的建立

针对某一个坐标系，作用在柔性单元上的广义力包括移动量f和转动量τ两个部分，可用一个力旋量F来表示［4］：F=（ f；τ） 。

机械手手爪中的各构件是一个独立的柔性单元，可看成是长度为L，密度为ρ，横截面积为A的均质梁，位于如图2所示的坐标系中，在静止状态下，只有末端作用一个力旋量F=（f；τ），在此力作用下，柔性单元产生的变形定义为变形旋量 W=（ δ；θ），其中 δ表示移动变形量，θ表示旋转变形量，那么均质杆柔性单元末端的变形就可以写成［5］

W（L）=（δx（L），δy（L），δz（L），θx（L），θy（L），θz（L））T。（1）式中：δx（L）、δy（L）、δz（L）分别表示长度为L的均质杆柔性单元在x轴、y轴和z轴方向上的移动变形量；θx（L）、θy（L）、θz（L）分别表示长度为L的均质杆柔性单元在x轴、y轴和z轴方向上的旋转变形量。

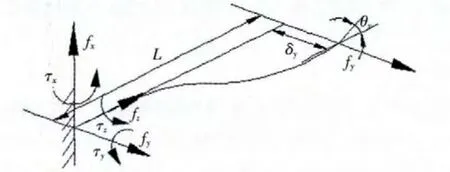
图2 静止状态下杆件的变形

沿着z轴方向的移动变形分量δz（z）、旋转变形分量θz（z）和力分量fz的关系式为：

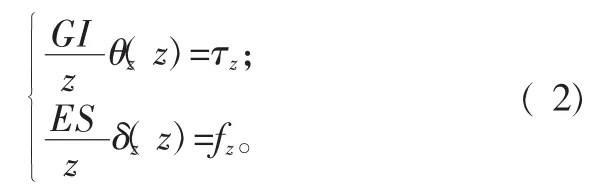
将力与弯曲变形投影到oyz平面，可得到oyz平面上移动量f和转动量τ两者之间的关系：

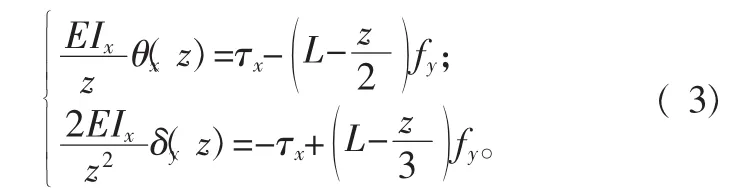
同样将力与弯曲变形投影到oxz平面，可得到oxz平面上移动量f和转动量τ两者之间的关系：

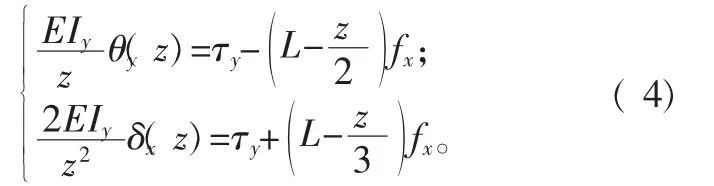
根据式（ 2）、（ 3）和式（ 4）可以得到杆件变形旋量 W（ L）和力旋量 F 之间的关系式：W（ L）=A（ L）F。A（ L）为均质杆柔性单元的空间刚度矩阵，令 z=L，A（ L）可用下式表示［6］：

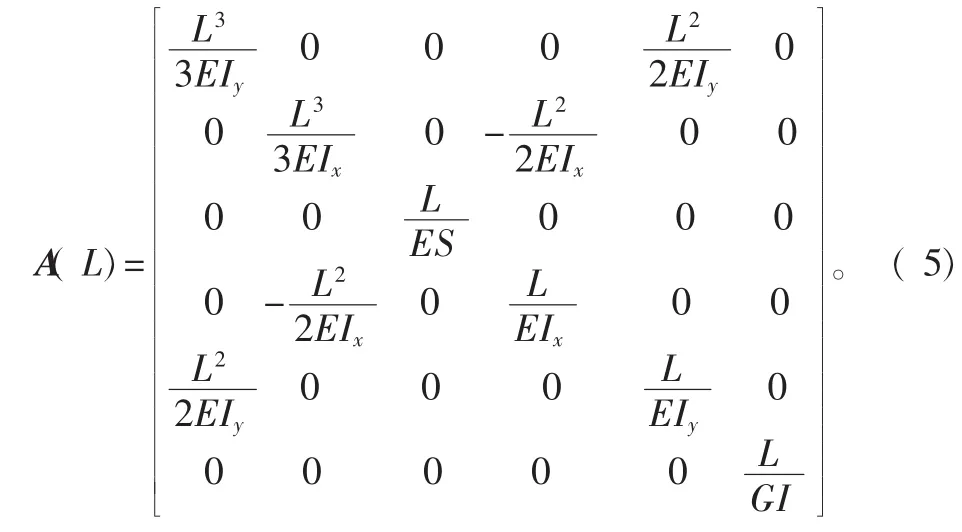
式中：E 表示材料的弹性模量；Ix、Iy、Iz分别表示均质杆柔性单元x、y、z轴的截面惯性矩；I表示截面极惯性矩；G表示均质杆柔性单元的剪切模量；L表示均质杆长度；S为截面积。

2.2 并联机构刚度分析

将机械手手爪进行简化后的机构图如图3所示，将参考坐标系原点定为C点，柔性单元均质杆材料为铝（E=70 GPa，G=25 GPa），截面为矩形，如图 3（ c） 所示，杆件长L=100 mm，厚h=3 mm，宽度b=10 mm，柔性单元分布圆半径a=40 mm，p=40 mm，倾角β=5°。当受到力旋量作用时，将下端所夹持零件的运动瞬心表现到空间任一点上，机构发生偏移或者旋转变形。从图中看出该机构由3个同样的柔性杆单元，均匀分布在一个圆周上，对于并联机构而言，末端刚度是先把所有支链的刚度变换到同一坐标系下，再把各个支链的刚度相加［7-8］。

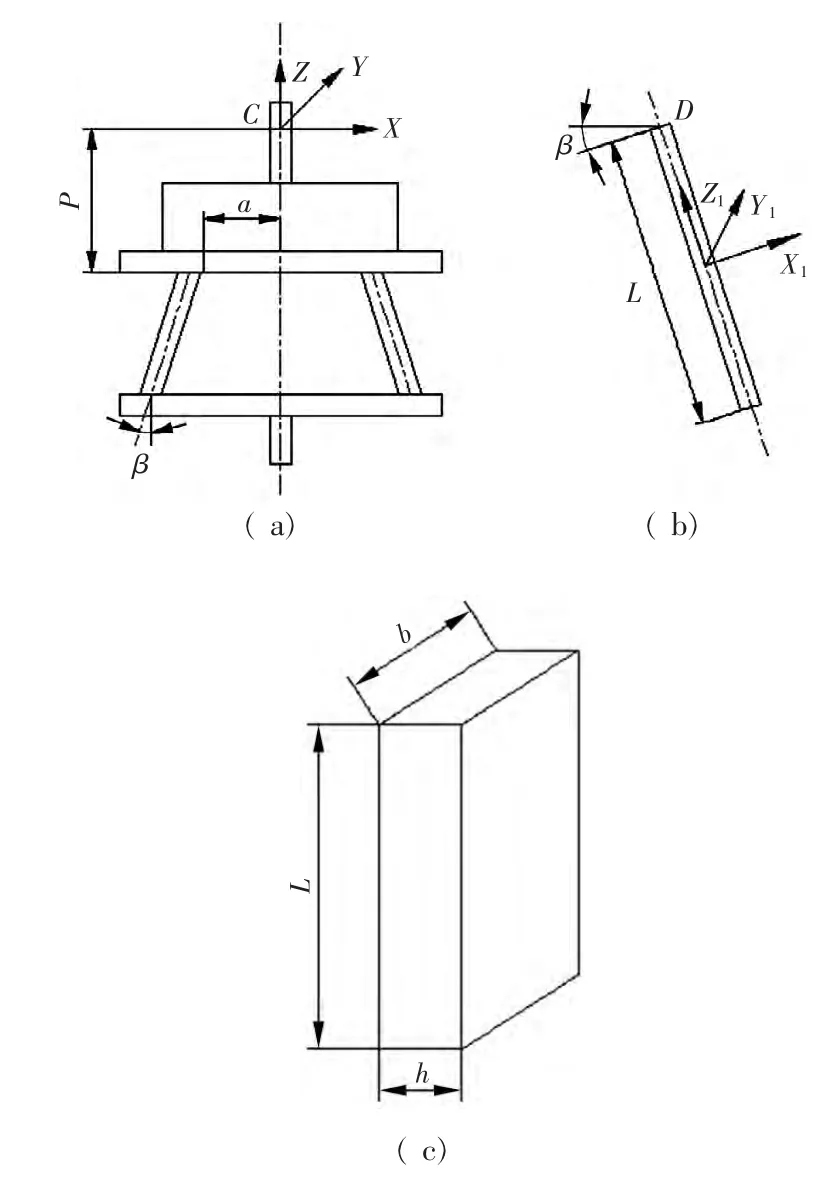
图3 机械手手爪机构简图

首先确定单个柔性单元的空间刚度矩阵，根据图3（b），先将该柔性单元的局部坐标取在其几何中心处，得出该单个柔性单元的刚度矩阵为

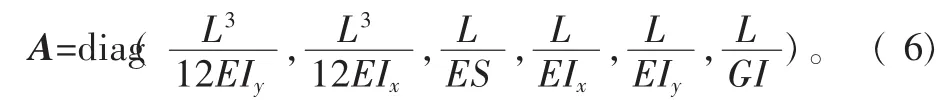
式中：E表示材料的弹性模量；G表示均质杆柔性单元的剪切模量；L表示均质杆长度；Ix=b3h/12、Iy=bh3/12分别表示均质杆柔性单元x、y轴的截面惯性矩；I=Ix+Iy=（b3h+bh3）/12 表示截面极惯性矩；S=bh 为截面积［9］。

再将坐标系平移到柔性单元的末端D处，根据式（5）可得到柔性单元在新坐标系下的刚度矩阵为

为了分析机构整体的刚度，需将所有柔性单元的刚度矩阵都变换到同一坐标系下，为了便于分析，假设C点与D点在同一平面上，机构在C处所受合力和合力矩为50 N和50 N·m，将机构已知参数条件代入式（7）得到单个柔性单元的刚度矩阵［10］：

整个机构的总刚度矩阵为3个柔性单元刚度矩阵相加，所以机构的总刚度矩阵为：

根据W（L）=A（L）F=（δx（L），δy（L），δz（L），θx（L），θy（L），θz（L））T可得到

由此得出整体机构在C处的平移变形量δ和旋转变形量θ。根据计算结果可以看出机构的移动变形量值远远小于旋转变形量值，符合设计要求。

3 结 语

在冲床机械手并联机构简图的基础上，利用旋量理论建立柔性单元的空间变形旋量与力旋量之间的关系式，得出单个柔性单元的刚度矩阵，并推导出机械手并联机构的总刚度矩阵。通过分析计算得出了机械手并联机构的平移变形量和旋转变形量值，此值可用来评价机械手的动态性能和末端的定位精度，为机构的进一步优化设计奠定了基础。

［1］ 周玉林，高峰.3-RRR 3自由度球面并联机构静刚度分析［J］.机械工程学报，2009，45（ 4） ：25-31.

［2］ 彭斌彬，李增明，武凯，等.二自由度平移并联机器人空间静刚度分析［ J］.南京理工大学学报，2012，36（ 3）：522-528.

［3］ 王殿君，冯玉倩.并联焊接机械手的静刚度分析［J］.机械制造，2013（ 1） ：22-23.

［4］ 刘玲玲，赵新华，李彬.一种三自由度并联机构刚度分析及仿真［ J］.天津理工大学学报，2011，27（ 4）：37-40.

［5］ 李辉，朱文白.柔索牵引并联机构的静刚度分析［J］.机械工程学报，2010，46（ 3）：8-15.

［6］ 王忠策，李蕴奇.基于旋量理论多关节柔性机器人操作臂的逆动力学模型推导与仿真［J］.吉林大学学报（理学版），2011，49（ 1）：98-104.

［7］ 王红旗，王泰华.基于旋量理论的移动机械手动力学建模［J］.兵工学报，2010，31（ 6） ：849-853.

［8］ 兰陟，李振亮，李亚.基于旋量理论的5-DOF上肢康复机器人雅克比矩阵求解［ J］.机械设计，2011，28（ 5）：51-53.

［9］ 汪选要，曹毅，黄真.冗余并联柔索机器人变刚度控制的研究［ J］.机械设计与制造，2014（ 4）：111-113.

［10］ 贾晓辉，田延岭，张大卫.3-PRR柔性并联机构动力学分析［J］.农业机械学报，2010，41（ 10） ：199-203.