三维尺寸链的偏差分析

张蕾

（合肥工业大学 机械与汽车工程学院，合肥 230009）

0 引 言

在实际生产制造过程中，很难制造出完美的零件，实际制造出来的零件往往与理想设计存在偏差，零件在装配过程中也会产生定位偏差，这些偏差在装配过程中不断累积，最终累积成产品的尺寸偏差。过度的尺寸偏差会导致产品失效或达不到预期目标，给生产制造带来损失。因此，如何及早地发现过大的尺寸偏差并提出优化方案就成为目前机械制造领域研究的热点。

目前，对尺寸偏差的分析大多建立在装配尺寸链的基础上。尺寸链是指在零件加工或总成装配过程中，由相互联系的尺寸按一定顺序首尾相连排列而成的封闭尺寸组，组成尺寸链的各尺寸称作尺寸链的环，有组成环和封闭环之分。通常把控制尺寸作为封闭环，已知尺寸作为组成环，然后通过已知尺寸的偏差计算出关键尺寸的偏差。这种方法在一维尺寸链上应用广泛，并取得了较多的研究成果［1-3］。但是目前对三维尺寸链的偏差分析大多为定性分析［5-7］，能给出明确的计算公式的文献相对较少且计算公式较为复杂［8］。

本文在前人研究的基础上，将每个零件尺寸看作三维空间中的有向矢量，利用空间矢量的矢量长度和空间姿态角来表示矢量，建立了三维尺寸链的计算公式，并得到了三维尺寸链的偏差传递公式。

1 三维尺寸链的偏差分析

1.1 三维尺寸链模型

在三维装配中，可以根据零部件间的尺寸关系和位置关系，确定零部件之间的装配点，然后将这些装配点依次相连，形成一个封闭的矢量环，如图1所示，这样，每一个零件都被简化成矢量环上的一个矢量。这个封闭的矢量环即为所需的尺寸链模型，需要控制的那个尺寸矢量即为封闭环矢量，其他的尺寸矢量即为组成环。

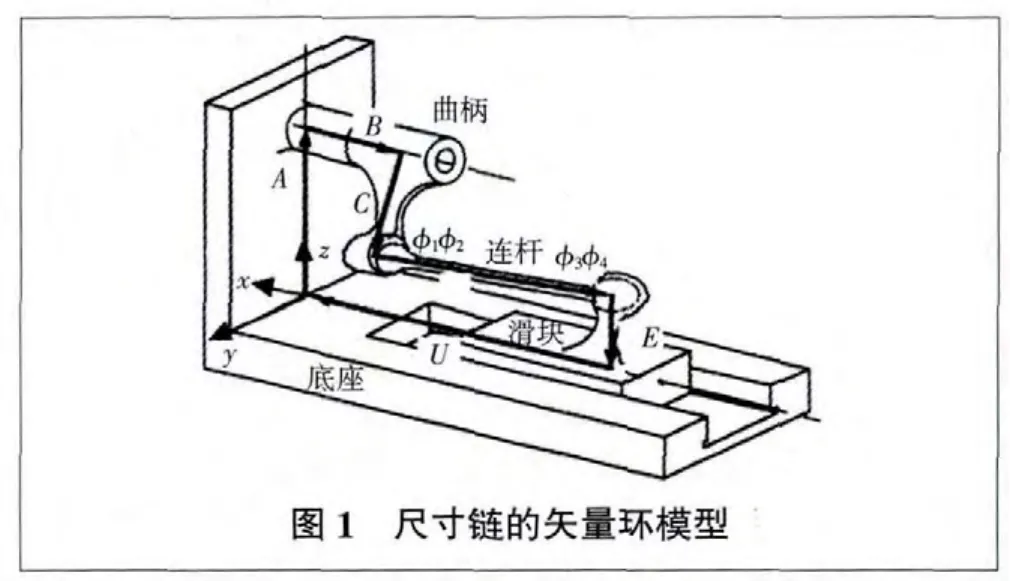
1.2 三维尺寸链计算公式

三维尺寸链可以看作是由三维空间中一个个的矢量前后连接而成，每一个矢量都可以用空间向量来表示。图2所示为简单的三维尺寸链，l→1和l→2为组成环向量，l→3为封闭环向量。该尺寸链的向量表示形式为：l→3=l→1+l→2。

在三维空间中，每一个向量都可以用三维坐标来表示。对于尺寸链各组成环来说，决定其空间向量坐标的有3个值，组成环的长度l、姿态角α、姿态角β，如图3所示。由几何关系可得：

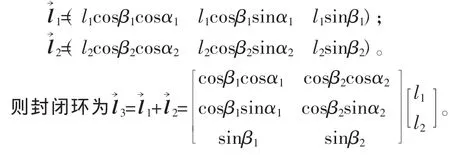
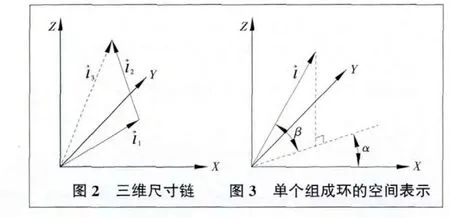
该尺寸链模型不仅适用于三维空间，同样适用于一维空间和二维空间。当β1=β2=0时，该公式则变为二维尺寸链计算公式当 β1=β2=0 且 α1=α2=0时，该公式则变为一维尺寸链的计算公式

1.3 三维尺寸链的偏差计算公式

三维空间中的组成环要比一维空间和和二维空间中的更复杂，它的偏差不仅包括尺寸链长度的变化Δl，还包括姿态角的变化Δα和Δβ，并且在尺寸链计算过程中还存在三角函数的运算，这使得三维空间中的偏差计算更为复杂。

假设图1中的组成环l→1和l→2分别产生了偏差Δl1、Δα1、Δβ1和Δl2、Δα2、Δβ2，此时组成环变为为l→1′和l→2′，其坐标式为：

由于 Δl、Δα、Δβ 的值均比较小，所以可认为 cosΔα≈1，cosΔβ≈1，sinΔα≈Δα，sinΔβ≈Δβ， 且认为 ΔαΔβ≈0，ΔβΔl≈0，ΔαΔl≈0。

则 cos（ β+Δβ）cos（ α+Δα） ≈cosβcosα-cosβsinαΔαsinβcosαΔβ，cos（ β+Δβ）sin（ α+Δα）≈cosβsinα+cosβcosαΔαsinβsinαΔβ，sin（ β+Δβ）≈sinβ+cosβΔβ。

最后，计算得到的封闭环为

1.4 敏感度矩阵

对应于偏差流理论［9］中的偏差传递公式 U=S·V，装配偏差矩阵为U=l→3′-l→3，偏差源矩阵为装配偏差对偏差源敏感度矩阵为S=

2 实例计算

下面以前大灯支撑侧板总成为例进行实例分析。图4所示为前大灯支撑侧板总成，该总成由4个零件装配而成，为了减少计算量，仅选取其中2个相连的零件进行分析。根据装配关系我们可以把每个零件简化成尺寸链上的一个组成环，图中A、B、C 3点为零件之间的装配点，因此可以用空间向量来表示这两个零件。 在由这两个零件组成的简单尺寸链中，为组成环，为封闭环，。

在空间坐标系，测得A点坐标为（-636.7384，-432.3098，320.0523），B 点坐标为（ -494.7559，-762.1346，311.3680），C 点坐标为（ -281.3382，-735.7764，518.5242）。可得组成环=（141.9825，-329.8248，-8.6843），l1=359.1920，α1=1.164 294，β1=-0.024 180， 组成环=（ 213.4177，26.3582，207.1562），l2=298.5893，α2=0.122 883，β2=0.766 729。 则组成环=（355.4002，-303.4666，198.4719）。可求得该尺寸链的偏差传递公式为

由敏感度矩阵可以看出，不同的偏差对封闭环尺寸同一方向的影响不同，同一偏差对封闭环尺寸不同方向的影响也不同。敏感度反映了各偏差源在偏差传递过程中被放大的倍数。以封闭环在X轴方向的投影为例，它对Δα1的敏感度为329.8248，也就是说姿态角α1的极小偏差传递到封闭环X方向时，将会被放大300多倍。同时，根据敏感度矩阵中数值的正负，我们可以判断出尺寸链上的增环和减环。敏感度矩阵直观地反映了零件偏差对装配偏差的影响，为后期进行公差优化提供了参考。

3 结 语

本文采用空间向量来表示尺寸链的各组成环和封闭环，并根据三维尺寸链的矢量关系，建立了三维尺寸链的偏差传递公式，得到了封闭环偏差对各组成环偏差的敏感度矩阵。

在尺寸链分析过程中，我们可以将所有零件根据装配关系简化成尺寸链上的一个个矢量，每个矢量由矢量长度和空间姿态角来进行坐标表示。在零件装配过程中，制造偏差和装配偏差直接反映为矢量长度的偏差和姿态角的偏差，各零件的偏差通过尺寸链传递到封闭环。

［1］ 蔡延波，曹增强，李志成．复杂装配尺寸链的分析计算［J］．现代制造工程，2008（ 4）：81-84.

［2］ 张黎，夏宏，魏小辉，等．飞机起落架收放机构静态装配的误差灵敏度分析［ J］．兵工自动化，2012（ 31）：17-20.

［ 3］ Li B Q．Computer aided design of assembly dimension chain of reducer ［C］//2010 International Conference on Artificial Intelligence and Education.2010.

［ 4］ Gao J，Chase K W，Magleby S P.Generalized 3-D tolerance analysis of mechanical assemblies with small kinematic adjustments［ J］.IIE Transactions，1998，30（ 4） ：367-377.

［5］ 王恒，宁汝新，唐承统．三维装配尺寸链的自动生成［J］．机械工程学报，2005（ 6）：181-187.

［6］ 彭和平，刘晓军．计算机辅助三维公差分析技术的研究进展［J］．制造技术与机床，2012（ 9）：43-47.

［ 7］ Shen Z，Ameta G，Shah J J.A comparative study of tolerance analysis methods ［ J］.Journal of Computing and Information Science in Engineering，2005，5（ 3）：247-256.

［ 8］ Davidson J K.Models for computer aided tolerancing in design and manufacturing［ C］//The 9th CIRP International Seminar on Computer-aided tolerancing，2005.

［ 9］ Hu SJ.Stream of variation theory for automotive body assembly［ J］.Annals of the Crip，1997，46（ 1） ：1-6.