交通网络储备容量的实用化求解方法

王诗琪，程 琳，邱占芝

(1.北京交通大学 交通运输学院，北京 100044;2.东南大学 交通学院，江苏 南京 210018;3.大连交通大学 软件学院，辽宁 大连 116028)*

0 引言

现阶段，城市化进程的加快导致城市居民出行量逐年递增，该增长趋势势必造成城市道路网规模、密度、等级级配及交通网络容量与现代城市交通发展产生供需矛盾.因此，路网规模与容量是城市规划发展过程中需要考量的指标.国外在交通网络储备容量方面的研究成果较成熟，研究方法包括时空消耗法，线性规划法，割集法，交通分配模拟法，狭义路网容量模型及供应分析法［1］.国内针对交通网络储备容量的研究起步较晚.高自友［2］、杨东源［3］、傅白白［4］等提出满足用户平衡和系统平衡的交通网络容量确定方法.曹莲英［5］等提出基于特定OD分布形态双层数学规划最优化模型.李晶，于雷［6］通过建立交通网络辅助图的方法计算交通网络容量.程琳［7-9］提出道路交通网络容量模型，分析比较基于路段容量的网络可靠性和基于结点容量的网络可靠性.

总的看来，国内研究者提出一些特殊情况下的交通网络储备容量的适用方法和修正模型，但在实际应用中未考虑交通拥堵的扩散性和传播性，同时未体现不同服务水平下交通网络储备容量的差异.因此，本研究在考虑路网服务水平的基础上，着重探索储备模型的修正方法，并利用某区域实际路网对修正模型进行验证.立意在于不仅可为路网容量模型找到新的探索角度，而且期望为解决我国道路基础设施规划建设中面临的实际问题提出新思路.

1 交通网络储备容量定义

现有交通网络储备容量的假设为“某个路段流量达到路段容量，就认为整个网络需求接近网络的容量”，本文认为该假设保守，没有挖掘出交通网络的潜质.例如，若路网中某路段发生拥堵，出行者可以不选择该路段，选择其他路径避免使用该路段，替代该路段满足出行需求.因此，需重新考虑达到交通网络储备容量的限制条件及因素.

定义1 交通网络储备容量:单位时间(1 h)内，在一定的道路和交通条件及服务水平的基础上，道路使用者自由选择路径后，交通网络能同时服务交通需求结构的最大值.

定义2 关键路段:基于一个给定的交通网络，在一定的道路和交通条件及服务水平的基础上，道路使用者自由选择路径后，达到或超过要求服务水平λ，即其饱和度大于等于服务水平λ对应的比区间小值端的路段.

定义3 关键交叉口:基于一个给定的交通网络，在一定的道路和交通条件及服务水平的基础上，道路使用者自由选择路径后，达到或超过要求服务水平θ，即其饱和度大于等于服务水平θ对应的V/C比区间小值端的交叉口.

定义4 关键路段组:基于一个给定的交通网络，在一定的道路和交通条件及服务水平的基础上，道路使用者自由选择路径后，如果路段a(a∈A，A为交通网络路段集合)的饱和度，即(V/C)a，与规定的服务水平 (V/C)λ满足:(V/C)a≥(V/C)λ，那么满足上述条件的路段a的集合为关键路段组.

定义5 关键交叉口组:基于一个给定的交通网络，在一定的道路和交通条件及服务水平的基础上，道路使用者自由选择路径后，如果交叉口b(b∈B，B为交通网络路段集合)的饱和度，即(V/C)b，与规定的服务水平 (V/C)θ满足:(V/C)b≥(V/C)θ，那么满足上述条件的交叉口b的集合为关键交叉口组.

定义6 关键路段组饱和:若关键路段组中的路段数量与交通网络总路段数A满足:

定义7 关键交叉口组饱和:若关键交叉口组中的交叉口数量b与交通网络总交叉口数B满足:，其中ξ为正数，则该交通网络达到饱和，即达到交通网络储备容量限制.

定义8 若该交通网络满足定义6与7中任意一项，则该网络均被视为达到饱和，即达到交通网络储备容量限制.

2 交通网络储备容量模型与算法

表示交通网络时，将其拓扑表现有利于科学计算与直观显示.视交叉口为点，路段为边，整个网络为一个有向图.为表示网络及容量问题，首先给出以下变量的定义:

G=(A，B)表示一个交通网络;Q为交通网络储备容量;ρ代表各个交通小区的基本交通产生量qrs的倍数乘子;ta为路段a的行程时间;Ca为路段a的通行能力;Va为路段a的流量;ta(0)为路段a的零流时间;α，β为特定参数，BPR建议α=0.15，β=4;T为所有路段的阻抗集合;k表示一条路径，k∈P;P为所有路径集合;Prs为r与s之间所有路径的集合，Prs∈P;r表示一个出发点，r∈R;R为所有出发点集合;s表示一个目的地，s∈S;S为所有目的地集合;fkrs为OD对(r，s)之间的路径k上的流量;qrs为单位时间段内从r到s的交通需求量;若路段a在(r，s)之间的路径k上，则δakrs等于1;否则等于0.

2.1 路段阻抗函数

路段的阻抗函数应能反映实际道路路段上行程时间与路段流量之间的关系，即流量越大，车速越低，行程时间越长.实际工作中较常用的路段阻抗函数是美国联邦公路局BPR阻抗函数:

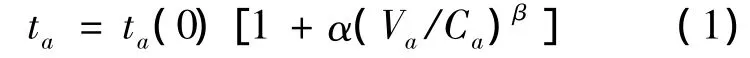
2.2 交通分配方法

交通分配是将OD矩阵中的交通需求按照一定的择路原则分配到交通网络上，得到路段流量.本论文采用用户平衡(User Equilibrium，简称UE)作为出行者路径选择的行为准则.该定理假定，所有出行者独立地做出令自己的行驶时间最小的决策，在所导致的网络流量分布状态里，同一OD对之间所有被使用的路径的时间是相等的，并不大于任何未被使用路径的时间.在这种状态下，任何人不能通过改变自己的路径来达到降低自己时间的目的.

2.3 路段饱和度及服务水平

对于城市道路来说，衡量交通服务水平的最主要指标为饱和度V/C，其次是车速(路段车速)或延误.由于车速延误与V/C有关，V/C增大，则车速降低，延误增加;V/C减小，则车速增加，延误降低，所以V/C是关键指标.为方便研究，可采用V/C作为城市道路的服务水平划分依据.饱和度计算方法如式(2).美国城市干线街道服务水平如表1，一条车道理论通行能力见《城市道路设计规范》.

2.4 交叉口饱和度及服务水平

交叉口按形状一般分为十字交叉口、T形交叉口、畸形交叉口和环形交叉口，按控制形式一般分为信号控制交叉口和无信号控制交叉口.不同种形状不同种控制形式的交叉口的通行能力计算法方法不同，参照《道路通行能力手册》在此不加赘述.交叉口饱和度计算方法如式(3).交叉口服务水平分级［10］如表2所示.

表1 美国城市干线街道路段服务水平

表2 交叉口服务水平［10］

2.5 交通网络储备容量模型

基于具有二层递阶结构的双层规划模型的基本原理，建立交通网络储备容量模型如式(4)所示.

2.6 交通网络储备容量算法

从运筹学角度来说，该模型属于双层规划模型.其中下层模型，即给定OD量的交通分配过程可通过TransCAD软件求解完成.

求解算法如下:

Step 1:建立路网G，确定初始交通网络出行OD矩阵;

Step 2:设定倍数乘子函数ρ(k)，令k=0，给定初始值ρ(0)=1，步长因子δ＞0;

Step 3:将 OD矩阵代入下层模型，利用TransCAD软件计算，得到各路段流量Va;

Step 4:判断是否满足上层规划中的约束:若满足，令 ρ(k+1)=δ× ρ(k)，k=k+1，转入Step 2;否则，停止迭代进入Step 4;

Step 5:输出ρ(k)与Q，算法结束.

3 实例分析与对比

该市区下辖3镇、2乡、9街道，79社区.2012年末，总人口为53.9万人.该市区把交通基础设施建设列为规划重点建设项目.在市域统筹协调项目建设计划中，明确提出改善市域交通条件，加强市域道路交通设施建设的指导方针.所以，研究其交通网络储备容量是非常必要的.可将研究过程归纳为以下几步:①划分交通小区，建立交通网络;②通过交通调查得到各小区出行OD量，各路段及交叉口基本信息;③按2.6节中描述的算法计算交通网络储备容量.

3.1 交通网络建立与初始情况分析

将研究对象划分为13个交通小区，并对路段及交叉口进行编码.通过居民出行调查，分析得到各小区高峰小时交通生成量(pcu/h)及OD出行矩阵，该原始OD矩阵可作为初始加载矩阵.通过利用TransCAD的交通分配模块，将初始OD出行交通量通过用户平衡算法分配至路网中，得到各路段及交叉口的流量及饱和度.基于分配结果，可计算得出各路段和交叉口的流量、饱和度及服务水平.

基于原始出行需求对路段及交叉口的分配结果进行分析，结论是研究区域内交通较为通畅，服务水平达A等级路段占88%，服务水平达A等级交叉口达68%.从上述数据可以看出，交叉口的饱和度对交通网络储备容量的影响更大.

3.2 确定倍数乘子ρ与结果分析

考虑研究对象实际路网运行情况，确定规定路段服务水平λ为D级，规定交叉口服务水平θ为D级，ε，ξ均取40.以0.1为步长值增大ρ，值分别为 1.1、1.2、1.3、1.4、1.5、1.6、1.7.其中，ρ=1.4、1.5、1.6 的分配结果如图1所示.

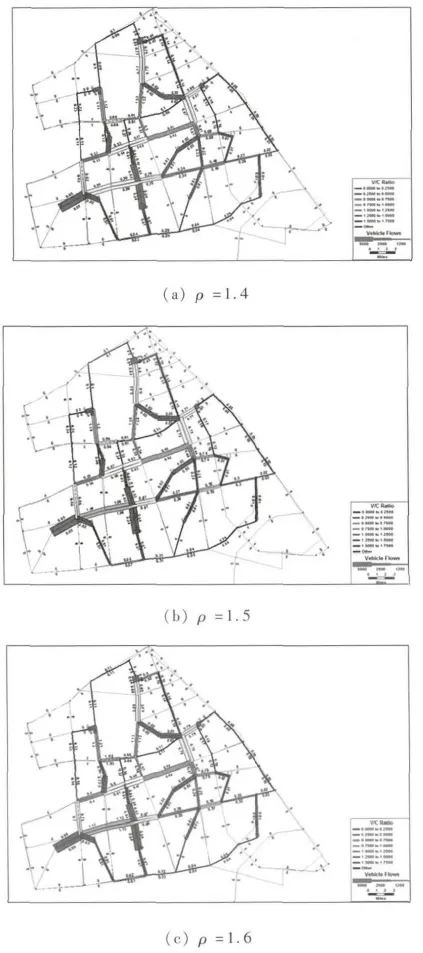
图1 研究区域路网交通分配结果

路段服务及交叉口服务水平D及D以上占总交叉口的百分比如表3所示.

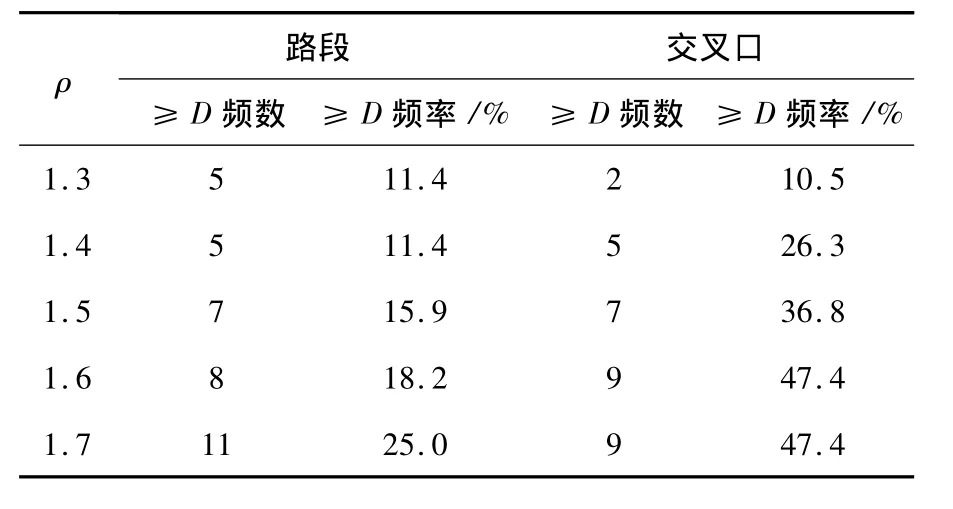
表3 路段及交叉口服务水平≥D数据统计表

通过路段与交叉口统计表对比，增大交通量对交叉口的影响程度较大，所以最终ρ值受交叉口限制.当倍数乘子ρ=1.0时，满足式(4).ρ=1.5为最终确定的倍数因子，路网达饱和，交通网络储备容量等于所有路段交通量之和，为25832 pcu/h.

随着值ρ的增大，交叉口差于D级服务水平的数量趋于稳定，这时路网大多数交叉口通行量接近交叉口的通行能力，饱和度趋于100%.当ρ值继续增大时，路段的服务水平继续降低，差于D级服务水平路段的数量也将趋于稳定，如图2所示.

图2 差于D级服务水平路段及交叉口频次图

可见，当路段饱和度趋于平衡时，所得的交通网络储备容量接近用时空消耗法所得结果37994pcu/h，在此对时空消耗法计算过程不做介绍.时空消耗法未考虑交通分布的合理性、交通网络服务水平等影响因素，与实际路网运行状况存在偏差.

综上所述，利用本论文提出的模型计算出交通网络储备容量，小于时空消耗法计算出的容量.本论文计算出的容量考虑服务水平与交叉口通行能力因素的影响，实用性更强.因此，本论文提出的交通网络储备容量计算方法具有一定实用价值.

4 结论

交通网络储备容量是交通规划中的一个重要指标，对它的研究可以对交通规划的许多方面提供新的研究手段和决策依据.总结本文所做的工作主要有:

(1)修订交通网络储备容量相关定义，根据服务水平、路段通行能力、交叉口通行能力三者结合判断交通网络容量是否达到饱和，并将其抽象并入模型，该限制条件的增加使计算结果更接近实际交通网络运行状况;

(2)建立基于服务水平和路段交叉口通行能力限制的交通网络储备容量模型，提出相关算法.利用TransCAD计算下层分配模型，实现交通量在交通网络上的分配，减轻下层模型计算的复杂度，使模型的实用性有所提高.结合某市区交通网络现状，利用本论文提出的方法计算出交通网络储备容量，与以往研究方法进行比较，验证了本方法的应用价值.

［1］HAI YANG，MICHAEL G H BELL，QIANG MENG.Modeling the capacity and level of service of urban transportation networks［J］.Transportation Research Part B，2000，34:255-275.

［2］四兵锋，高自友.城市交通超级网络均衡配流模型计算法［J］.公路交通科技，1998，15(5):67-71.

［3］杨东援，马哲军.交通网络容量分析的理论与方法［C］.中国土木工程学会第七届年会暨茅以升诞辰100周年纪念会，上海，1995:128-133.

［4］傅白白.效能网络系统最优分配模型分析与应用研究［D］.大连:大连理工大学，1999.

［5］曹莲英，王作杰，彭国雄.基于特定OD分布意义上的交通网络容量分析方法［J］.山东交通学院学报.2003，11(2):3-6.

［6］李晶，于雷.基于Visum的交通网络容量计算理论研究［J］.城市交通，2006，4(2):68-73.

［7］程琳，王炜，王京元，等.城市道路交通网络容量、交通规划和交通管理［J］.公路交通科技，2005，22(7):118-122.

［8］程琳，王炜，于春青，等.城市道路交通网络容量的建模［J］.管理工程学报，2007，21(2):84-88.

［9］程琳，李强，王京元，等.城市道路交通网络容量可靠性研究［J］.东南大学学报(英文版)，2004，20(2):235-239.

［10］王爽，周彤梅.信号控制交叉口服务水平的评价方法研究［J］.中国人民公安大学学报(自然科学版)，2007(3):78-79.