基于一对多建筑供应链材料允许缺货下的联合库存优化

钟德强，郭 薇

（湖南工业大学 管理科学与工程研究所，湖南 株洲 412007）

1 引言

近几年，随着我国城镇化战略的实施，建筑业得到了迅猛发展。在施工技术日益完善的今天，成本控制成为了重中之重。而建筑材料作为占施工造价60%左右的基础物质，由于其需求可提前计算，成为了控制造价的重要对象。降低建筑材料的库存成本成为控制总成本的有效途径。供应链管理思想在制造领域的成功给建筑业的成本管理带来了新的契机。

目前，国内外专家学者对建筑供应链及联合库存的研究还处于起步阶段。郭大宁[1]提出，库存控制的最优化目标不仅是供应链环节中某一个或某几个节点企业的库存最优化，而是整个供应链环节有机、协调、一体化库存的最优化。叶吉庆[2]将联合库存思想引入建筑供应链中，以期提高建筑供应链库存水平，从而提高建筑企业竞争力。以上文献大都只是从理论上阐述了联合库存的优越性，并未给出具体的数学建模进行验证。张伟伟[3]建立了一个不允许缺货、补充时间极短的简单联合库存管理模型。但是该模型情况特殊，不满足建筑材料供给情况。肖燕[4]在其基础上，考虑了有初始库存、允许库存短缺、缺货需立即补充的情况，建立了合理的库存成本模型。邵必林[5]建立了建筑供应链环境下的库存成本控制模型，并与传统模型进行比较，证明了联合库存比传统模型更加节约成本。朱宏[6]证明了短期激励下，供应商管理库存增加了供应商相关成本，应该采取相应的措施激励供给双方采用联合库存。

以上文献给出的模型存在以下缺陷：一是只考虑了一个施工方与一个供应商的情况，而建筑供应链环境下，多使用总承包商概念，总承包商将任务分包给若干分包商，因此，一个总承包商与多个分包商更符合实情。二是采用联合库存存在供应链总成本减少，但各方成本有增有减的情况，因此应该考虑对节约的成本进行合理分配。本文研究一个总承包商与多个分包商的联合库存问题，建立一个一对多的联合库存成本模型，比较传统独立库存与联合库存的成本，并用Shapley 值法对联合库存节约的成本进行分配。

2 模型建立

该模型是包括一个总承包商、n 个分包商的模型系统，分包商发生材料需求，向总承包商反映。供应链中各方组成一个联合库存，共同制定订货批量，分担成本与风险。

假定D 为需求率（即单位时间需求量，单位时间为日）；Q为订货经济批量；Q1为初始存储量；Q2为缺货量；t1为不缺货时间；t2为缺货时间；H为单位时间存储费；K为单次订购费；S为单位时间缺货费。允许缺货，即一次订货可分为两次送达，第一次送货量为Q1，第二次送货量（即补送货量）为Q2。补足缺货后仍有Q=D×t，不缺货时间，缺货时间

其模型示意图如图1所示。

图1 允许缺货的经济批量补货系统

假定：

（1）分包商在施工过程中对产品的需求是连续均匀的，即需求速率为常数；

（2）总承包商的单位时间存储费不变，每次订货量不变，每次订货费不变；

（3）分包商的单位时间存储费用不变，每次订货量不变，每次订货费不变；

（4）考虑到实际情况，允许缺货，缺货须立即补充，对缺货损失可以定量化研究，单位时间缺货费不变；

（5）分包商与分包商、分包商与总承包商相互独立。

2.1 传统独立库存模型

在传统独立库存模型中，分包商为强势方，可以根据自己的资金情况和利润最大化原则来确定经济订货批量，分包商的单位时间库存成本为：

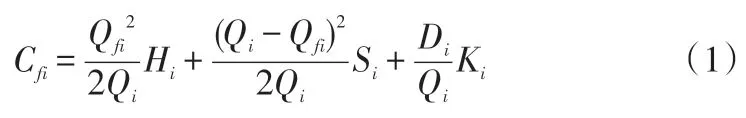
其中，Qfi为传统独立库存下分包商i 的初始存储量；Hi为分包商i的单位时间存储费；Si为分包商i的单位时间缺货费；Ki为分包商i的单次订购费。Di为分包商i对材料的需求率；Qi为传统独立库存下分包商i的订货经济批量。

将式（1）对Qfi求导，并令其等于零，得到初始存储量Qfi：

将式（2）代入式（1），并对Qi求导，同样令其等于零，得到经济批量Qi：

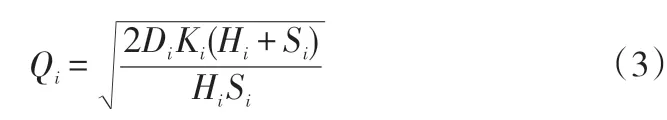
将式（2）、式（3）代入式（1），得到分包商最小单位时间成本Cfimin为：

总承包商为供应链中的弱势方，只能被动接受分包商的订货批量Qi，且初始存储量也等于分包商的初始存储量（Qfi），总承包商的单位时间库存成本为：

其中，H 为总承包商的单位时间存储费；S 为总承包商的单位时间缺货费；K为总承包商的单次订购费。

将式（2）、式（3）代入式（5），得：

传统独立库存下单位时间总成本为总承包商与分包商单位时间成本之和，则单位时间总成本为：

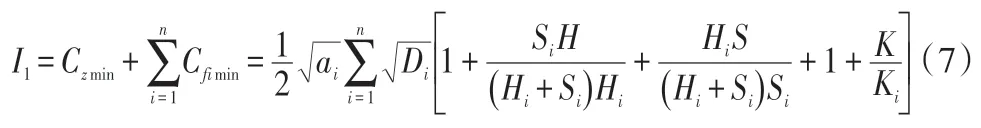
2.2 联合库存模型

在联合库存模型中，总承包商和分包商的初始存储量、缺货量及订货经济批量相同，由供应链各参与方共同协商，其目的是使各节点企业对批量的需求保持一致，消除库存放大效应和不确定性，实现风险共担和整体供应链利润最大化。单位时间联合库存成本为：

Ai为联合库存下分包商i的初始存储量；Qui为联合库存下分包商i 的订货经济批量。将式（8）对Ai求导，令其等于零，得：

将式（9）代入式（8），对Qui求导，得：

将式（9）、式（10）代入式（8），得：

2.3 单位时间传统独立库存成本与联合库存成本的比较

单位时间联合库存成本小于单位时间传统独立库存成本，联合库存方式能减少供应链库存成本，这说明就供应链总体而言，联合库存方式可行。

3 算例分析

本文以一个总承包商、两个分包商为例，I 可以看成由三个节点企业组成的联盟体，s 为联盟体I 的联盟子集，Si是I 中包含i 企业的所有联盟子集。υ（s）为联盟子集产生的效益，υ（s）-υ（si）表示企业i 对子集s 的效益所做的贡献大小。,其中，|s|表示子集的数量，n 表示参与合作的对象数量。将总承包商、分包商1、分包商2 分别记为B、1、2，相关参数如下：K=2 100元/次，H=20元/t/日，S=10元/t/日，D1=300t/日，K1=1 000 元/次，H1=15 元/t/日，S1=5 元/t/日，D2=400t/日，K2=1 800 元/次，H2=16 元/t/日，S2=8 元/t/日，则联合库存前各方成本:总承包商成本：Czmin=6 298.843；分包商1 成本:：Cf1min=1 500；分包商2 成本：Cf2min=2 771.281；库存总成本：I=10 570.124。

（1）三个企业联合库存：I(z,1,2)=10 538.099。在三者联合库存中，如果均摊，则每家企业摊得3 512.7，这对分包商来说，比单独库存时的费用还要大，显然分包商不愿意。故要用Shapley值法来分配效益[7]。

（2）总承包商与分包商1 联合库存，分包商2 单独库存：I(z,1)=10 539.351。

（3）总承包商与分包商2 联合库存，分包商1 单独库存：I(z,2)=10 568.823。

故υ(⊄)=0；υ(z)=υ(1)=υ(2)；υ(z,1)=I-I(z,1)=10 570.124-10 539.351=30.773 ；υ(z,2)=I-I(z,2)=10 570.124-10 568.823=1.301 ；υ(z,1,2)=I-I(z,1,2)=10 570.124-10 538.099=32.025 。其具体分配见表1-表3。

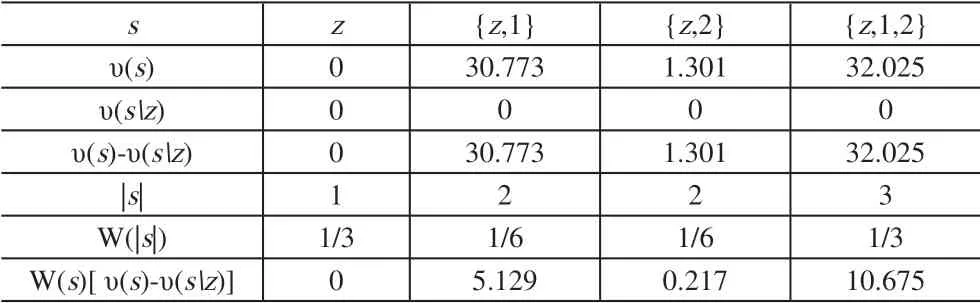
表1 总承包商的利益分配表

由表1 可得，联合库存下总承包商分配的利益为φz(υ)=0+5.129+0.217+10.675=16.021。

表2 分包商1的利益分配表

由表2 可得，联合库存下分包商1 分配的利益为φ1(υ)=0+5.129+0+10.241=15.37。

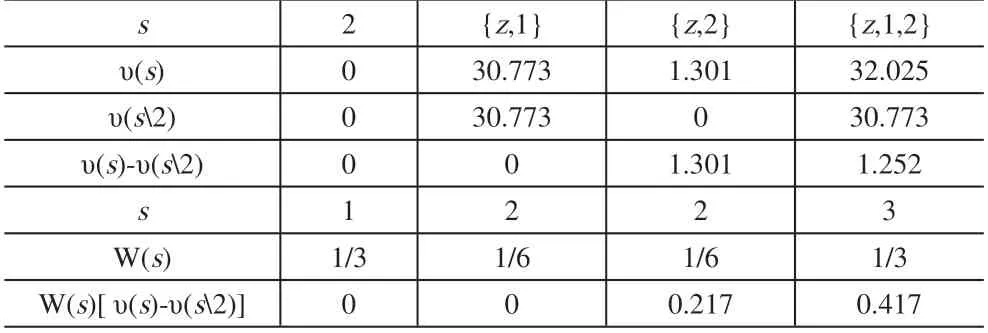
表3 分包商2的利益分配表

由表3 可得，联合库存下分包商2 分配的利益为φ2(υ)=0+0+0.217+0.417=0.634。

容易验证，φz+φ1+φ2=32.025。这种分配不是简单的平均分配,而是基于各合作伙伴在合作联盟经济效益产生过程中的重要程度来进行分配的一种分配方式，有一定的合理性和优越性。最后，在供应商管理库存总成本10 538.099 中，各企业的费用分担分别是：

（1）总承包商成本为：Czmin-φz(υ)=6 298.843-16.021=6 282.822；

（2）分包商1的成本为：Cf1min-φ1(υ)=1 500-15.37=1 484.63；

（3）分包商2 的成本为：Cf2min-φ2(υ)=2 771.281-0.634=2 770.647。

可以得出三家企业合作比单独一家或任意两家合作分摊的费用少，于是三家加入联盟的积极性比较高,联盟的稳定性也比较好。

这里φz(υ)=16.021，φ1(υ)=15.37，φ2(υ)=0.634，φz＞φ1＞φ2，这说明在三者的合作中，总承包商的贡献最大，其次是分包商1，贡献最小的是分包商2。

4 结论

本文在原有联合库存模型的基础上，将其发展成一个总承包商和多个分包商的形式，并通过对比得出，在存在多个分包商时，联合库存成本仍然比传统独立库存成本低，证明了联合库存模型适用于多个分包商的情形，使联合库存模型在实际应用中得到拓展。最后用Shapley值法对节省的库存在各节点企业间进行分配，使各节点企业共享联合库存带来的成本节约。

[1]郭大宁,张健.供应链管理中的联合库存控制[J].东华大学学报(自然科学版),2003,29(5):63-66.

[2]叶吉庆,李锦飞.浅析建筑供应链管理中的联合库存管理（JMI）[J].商场现代化,2007,(16):144-145.

[3]张伟伟.基于供应链环境下联合库存管理研究[J].价值工程,2005,(8):30-32.

[4]肖燕.供应链环境下联合库存管理的库存成本模型[J].重庆工学院学报(自然科学版),2007,21(10):119-123.

[5]邵必林.建筑供应链管理下库存成本控制模型[J].物流技术,2012,31(12):376-378.

[6]朱宏,郭海峰,黄小原.供应商管理库存的利润模型及其优化策略[J].东北大学学报,2004,25(5)：505-507.

[7]刘建芬,胡奇英.基于Shapley 值法的VMI 下合作企业间的费用分担策略[J].系统工程,2005,23(9):80-84.